亲历知识探究过程 感悟数学思想方法
2017-06-08马新丰
马新丰

摘 要:小学数学教学不仅要关注学生的数学知识形成过程,关注学生是否能理解并尝试运用数学知识解决问题,还应特别关注在引导学生亲历知识探究过程中对数学思想方法的感悟。本文尝试在引导学生亲历知识导入过程、知识形成过程、例题导引过程、归纳总结过程与回顾反思过程等环节,加强数学思想方法渗透,使学生的数学思维和数学探究能力在亲历知识的探究过程中得到切实、有效的发展。
关键词:小学数学;亲历探究;思想方法
小学数学教育在学生成长过程中有着非常重要的地位,是激活学生的数学思想方法,让学生在学习数学和应用数学解决问题的过程中学会和掌握最为重要的、必须学习的数学知识、思想方法的重要阶段。《小学数学新课程标准》也明确指出:“数学课程内容不仅包括数学的结果,也包括数学结果的形成过程和蕴涵的数学思想。”这一阐述对小学数学教学提出新的要求,小学数学教学不仅要关注学生的数学知识形成过程,关注学生是否能理解并尝试运用数学知识解决问题,还应特别关注在引导学生亲历知识探究过程中对数学思想方法的感悟,让学生的数学思维和数学探究能力在亲历知识的探究过程中得到切实、有效的发展。
一、亲历数学知识导入过程,感悟数学思想方法
小学数学教学存在很强的逻辑性,它由浅入深,新旧知识环环相扣,开合自如。这一编排特点决定了数学知识导入过程的重要性,有效的知识导入将有助于提升数学课堂的有效性与成功率,也是激发学生学习兴趣,感悟数学思想方法的重要途径。
1. 数学史导入数学知识
数学作为一门自然科学,伴随着人类的出现而诞生,在长期的发展中形成了悠久的数学发展史。小学数学教师要善于引导学生亲历“数学史”导入过程,亲历数学知识、数学思想方法的形成过程,自然地渗透数学方法。
例如在教学加、减、乘、除运算时,我们可以借助我国“算筹”发展史导入,尽管算筹准确的产生年代已经不可考察,但是据史料记载在春秋时代已经非常普遍,分为纵、横两种方式:表示一个多位数字时,采用十進位值制,各位值的数目从左到右排列,纵横相间,并以空位表示零。算筹为加、减、乘、除等运算创造了良好的条件。
通过引导学生亲历“数学史”,将算筹法与今天加、减、乘、除运算进行比较式探究,不仅使学生形成联系、发展的数学思想方法,也有效激发了学生数学学习兴趣与民族自豪感。
2. 问题建模引入数学知识
问题建模是数学常用的一种方法,它改变传统数学教学方法,将数学概念、方法等模型化,既引导学生掌握数学基本原理、法则,又提升学生运用数学知识解决实际问题的能力。运用问题建模来导入数学知识,将构建起知识呈现的背景,由抽象到具体,符合小学生数学学习认知特点。
例如《鸽巢问题》,笔者以一个问题建模来导入本课。教学例1:4支笔,3个筒,可以怎么放?请同学们用实物放一放,看有几种摆放方法?答案为(4,0,0),(3,1,0) ,(2,2,0),(2,1,1)。这样设计的意图在于将抽象的鸽巢问题形象化,在学生亲历具体操作,枚举所有情况后,去理解“总有一个筒里至少放进了2支笔”,不仅激发学生探究兴趣,也有机渗透化归与转化思想。
二、亲历数学知识形成过程,感悟数学思想方法
数学知识经历了一个不断发展、不断完善的过程,也是数学思想方法不断提炼、完善的过程。引导学生亲历数学知识形成过程,不仅有助于学生了解基本的数学知识,也有助于学生思想方法的发展,不仅知其然,而且知其所以然。
1. 亲历概念形成过程
数学概念是数学内在属性的高度概括,它是人们从感性认识上升到理性认识的思维成果。引导学生亲历数学概念探究的过程,有助于学生洞悉数学知识的内涵与外延,促进学生数学知识的内化,潜在地使学生感悟到数学概念中蕴含的数学知识方法。
例如二年级“平均分”概念教学,笔者根据小学二年级学生的认知特点,引导学生亲历概念的形成过程。
教师先呈现6个苹果,让学生任意分成几堆,自己摆一摆。然后由学生动手操作,用图画记录结果,利用实物投影仪展示出来,可能有:分成3堆,每堆2个;分成3堆,一堆1个,一堆2个,一堆3个;分成2堆,一堆2个,一堆4个;分成2堆,每堆3个……
最后开始探究“平均分”。引导学生观察分法,提出思考:你们能根据每份分的个数相同与不同,把这些分法分成两类吗?在学生亲历过程中,得出平均分的概念:我们发现其中两种分法的每一份的数目都是相同的,我们把这样的每份分得同样多的分法,叫作“平均分”。通过亲历探究,学生不仅了解平均分的概念,也运用数形结合的思想完成概念探究。
2. 亲历定理公式探究过程
数学定理、法则、公式等,体现了数学思维成果,是数学家在实践中得出的数学结论,是学生学习数学、发展数学思想方法的基础。传统教学中,教师往往采用填鸭式教法,学生了解了定理、法则与公式,但是“消化不良”,难以将之转化为学生自己的思想方法。引导学生亲历其探究过程,则是学生学习定理、公式与法则的“消食剂”。
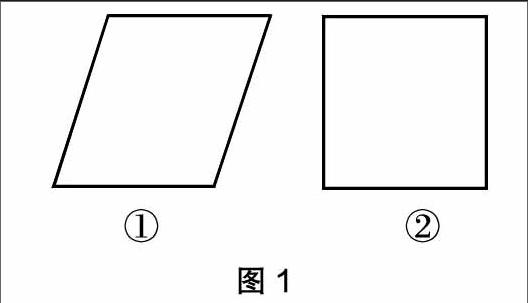
例如平行四边形公式,S=ah,公式中h为高,a为底,S为平行四边形面积。概念比较简单,但是学生不理解就容易出现消化不良。为此,笔者引导学生对公式进行探究推导:
(1)如图1①,这个平行四边形的面积是多少平方厘米?
(2)它的底是多少厘米?
(3)它的高是多少厘米?
(4)这个平行四边形的面积跟它的高与底有什么关系?
(5)请同学们猜一猜:怎样计算平行四边形的面积?
在推导过程中,学生通过剪拼把平行四边形转化成了长方形(如图1②),解决了问题。在公式推导过程中运用了“转化的数学思想方法”,对于学生学好数学具有很重要的帮助。
3. 亲历开放题型探究过程
开放性题型是指题目的条件、解题方法与结果等具有不明确性,是根据问题情境进行解答的一种题型,它最显著的特点是开放性,能有效训练学生数学思维,培养学生数学思想方法。
例如在学习 “百分数应用题”后,可以设计这样的题目:一个家庭去某地旅游,甲旅行社的收费标准是:如果买3张全票,则其余人按半价优惠;乙旅行社的收费标准是:家庭旅游算团体票,按原价的80%优惠,这两家旅行社的原价均为每人1000元。
(1)如果你家去,你准备选择哪家旅行社呢?
(2)看到这些信息后,你对其他去旅游的家庭有什么建议呢?
学生在解答这类题目时,需要调动数学思想方法,在亲历过程中,学生的思维将摆脱常规思维的束缚,培养学生发散性思维,丰富学生解题思想方法。
三、亲历总结与反思过程,感悟数学思想方法
总结与反思是对数学学习的进一步深化,能引导学生将所学的零碎知识进行归纳、总结,形成系統性知识,并通过有效反思,对数学学习进行重新审视。
1. 亲历归纳总结过程
数学思想方法遍存于数学学习的全过程,这就需要教师在数学教学中有意识地引导学生亲历归纳与总结学习过程,挖掘隐性存在于数学学习中的思想方法。从而有计划、有目的性地对学生进行数学思想方法训练,形成系统的数学思维,这样才能有效提升学生运用数学知识解决实际问题的能力。
例如在学习完扇形统计图后,笔者引导学生对小学阶段的统计图知识进行归纳总结:条形统计图,能够轻易地看出各种数量的多少;折线统计图不但能表示数量的多少,而且还能表示数量增减变化;扇形统计图则能够清楚地表示出各个部分数量与总数之间的关系。通过归纳总结,不仅有助于发展学生分类与整合的思想,而且有助于增强学生对统计图的认识,根据实际情况灵活地选用统计图。
2. 亲历回顾反思过程
回顾反思的过程是学生对数学学习进行梳理与重构的过程。学生不仅对学习成果进行内化,同时对学习过程中存在的不足进行自我“反刍”。在亲历回顾反思的过程中,学生形成的数学思想方法将与学生主体进行深度融合,从而形成自己的数学思想方法,而不再是数学思想方法的“器皿”。
例如“鸡兔同笼”内容,如何引导学生加深对“鸡兔同笼”的理解呢?教师不妨引导学生反思这一类题目的解答方法,结合画图来辅助解答。
通过画图(如图2),可以直观地看到有2只鸡,4只兔。这样就能够化难为易,同时激发学生学习兴趣,培养学生数形结合的思想。
总之,数学思想方法或显性或隐性地普遍存在于小学数学学习中,数学教师要进一步强化数学思想方法意识,注重激发学生主体意识,强化学生学习体验,在亲历知识探究与体验中,有计划、有目的、循序渐进地培养学生数学思想方法,促进学生素养的发展,为小学生数学学习奠定坚实基础。
