全向辐照电磁环境构建及与BPSK系统的干扰效应研究

贾锐，王川川，赵琳锋



全向辐照电磁环境构建及与BPSK系统的干扰效应研究

贾锐，王川川，赵琳锋

（电子信息系统复杂电磁环境效应国家重点实验室，河南 洛阳 471003）

目的分析某型通信电台在工作时所处的复杂电磁环境，构建基于混响室原理的全向辐照电磁环境。方法以一个采用标准BPSK信号的数字通信系统为例，研究干扰信号码速、频率偏移量、信干比等参数对系统误码率的影响。结果当干扰信号码速低于期望信号码速时，随着频率偏移量的增加，接收系统误码率也随之减小，且呈现周期性规律；当信干比相同时，在相同的频率偏移下，干扰信号的码速越高，其干扰效果越好；当干扰信号码速高于期望信号码速时，随着干扰信号码速的进一步增大，干扰效果将呈现逐渐降低的趋势。结论该研究在电子装备的复杂电磁环境适应性方面做出了有益探索，为今后的复杂电磁环境适应性理论的深入研究提供了借鉴。

全向辐照；统计特性；误码率；码速；频率偏移量；信干比

通常情况下，电子装备面临的电磁环境干扰主要有以下四类：一是有意干扰，暨敌方针对我方电子装备的精确电磁干扰；二是敌方对我方电子装备进行的压制式干扰；三是我方电子装备工作中形成的自扰互扰电磁环境；四是装备所处环境的背景噪声电磁干扰[1—5]。这些电磁信号共同存在形成了对电子设备的工作性能造成影响的复杂电磁环境。2008年GJB 6520颁布了《战场电磁环境分类与分级》，将电磁环境分为简单电磁环境、轻度复杂电磁环境、中度复杂电磁环境、重度复杂电磁环境四类，分类是在分析电磁环境的频谱占用度、时间占有度和空间覆盖率的基础上得出的。战场环境的一大特点在于其未知性，战场环境是由多个因素共同作用而成，其中任意参数发生变化，所形成的战场环境就会相差甚远。战场电磁环境是其中一部分，受到地杂波、海杂波、云层反射、周围建筑物等自然条件的影响，无法事先确切摸清其分布规律和特点。这就种未知性就要求在进行电子装备复杂电磁环境适应性试验时，要充分考虑装备在未来战场上面临的所有复杂电磁环境[6—8]。

目前，通过仿真模拟手段所能构建的复杂电磁环境中，基于混响室原理的“全向辐照”电磁环境[9—11]，从频谱占用度、时间占有度和空间覆盖率等因素分析，都是其中最为复杂的、也是干扰威胁最大的电磁环境之一。此外，这种电磁环境与通信电台战场电磁环境相似。美国电磁环境效应实验室利用混响室进行通信装备测试[12]；意大利学者利用混响室模拟地杂波频谱特性[13]；国内军械工程学院利用混响室模拟了地杂波、海杂波的频谱特性和幅度特性[14—15]。因此，文中就将某型通信电台置于全向辐照的电磁环境中，研究其适应性试验技术和干扰机理。

1 混响室全向辐照电磁环境

全向辐照电磁环境是指受试装备在测试期间，将会受到周围360°范围的电磁干扰。典型机械搅拌混响室的结构为高导电率的屏蔽腔体内装配一个或多个由高导电率金属建造的机械搅拌器，其目的是在连续或步进转动的过程中对腔室内电磁场产生一定的扰动，通过其边界条件的持续改变，达到改变腔室内部电磁场模结构的目的，使混响室工作于过模状态，从而得到统计均匀、各向同性、随机极化的电磁场分布。其电场分布规律如图1所示。

由于混响室属于电大尺寸，在构建其电磁环境时，会受到计算资源的约束，无法进行快速有效的运算。因此，考虑采用基于统计理论的蒙特卡洛方法，利用平面波叠加理论对其进行模拟。使入射电磁波方位角和俯仰角满足[0, 2π]的随机分布。根据电场理论，其极化角服从区间[0, π]内的随机分布，其相位服从区间[0, 2π]内的随机分布，如图2所示，可模拟全向辐照电磁环境。通过与理想混响室内电场分布规律的统计分布规律对比（如图3所示），表明所构建电磁环境与混响室内电磁环境一致。

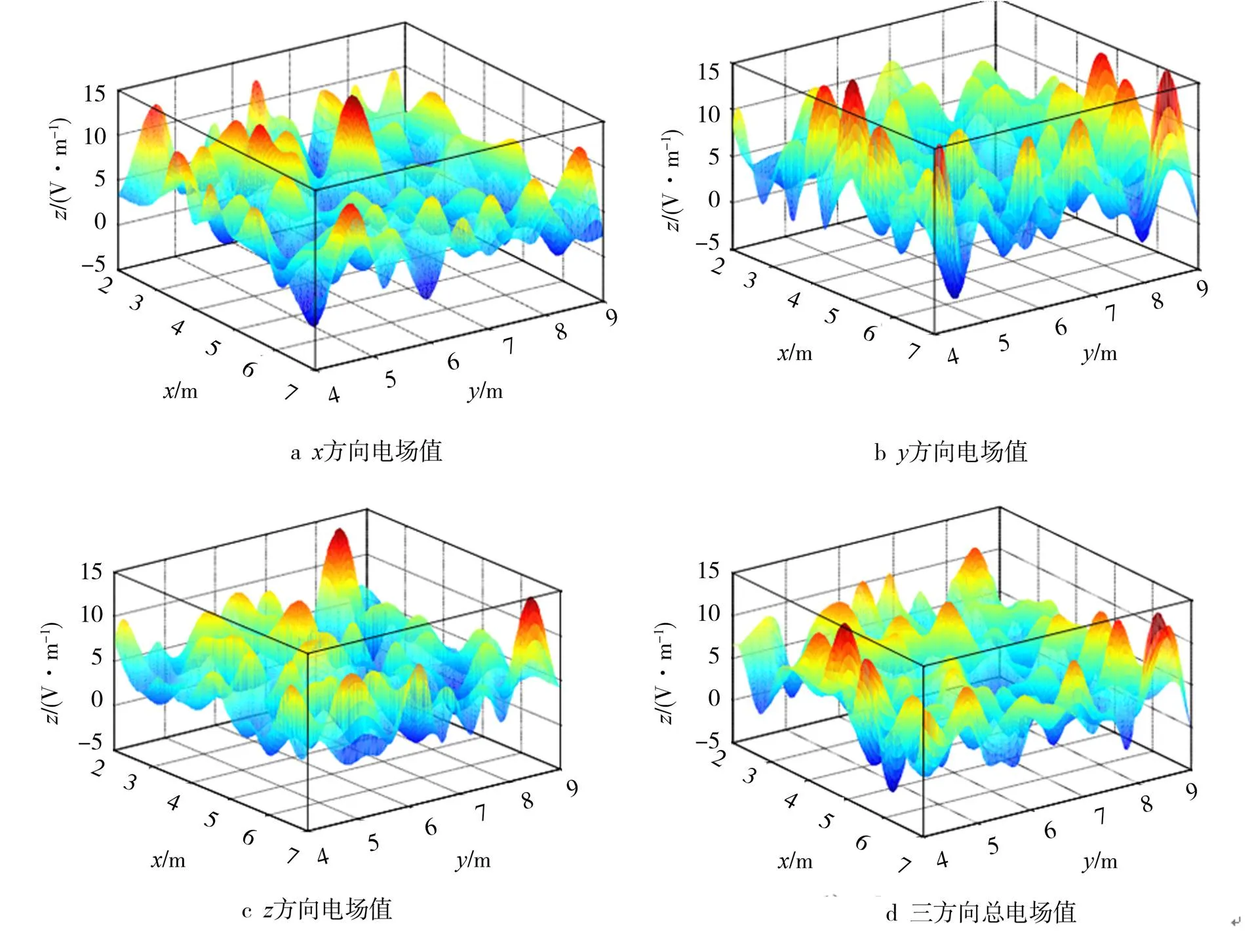
图1 混响室工作区域电场分布规律

图2 随机入射电磁波示意

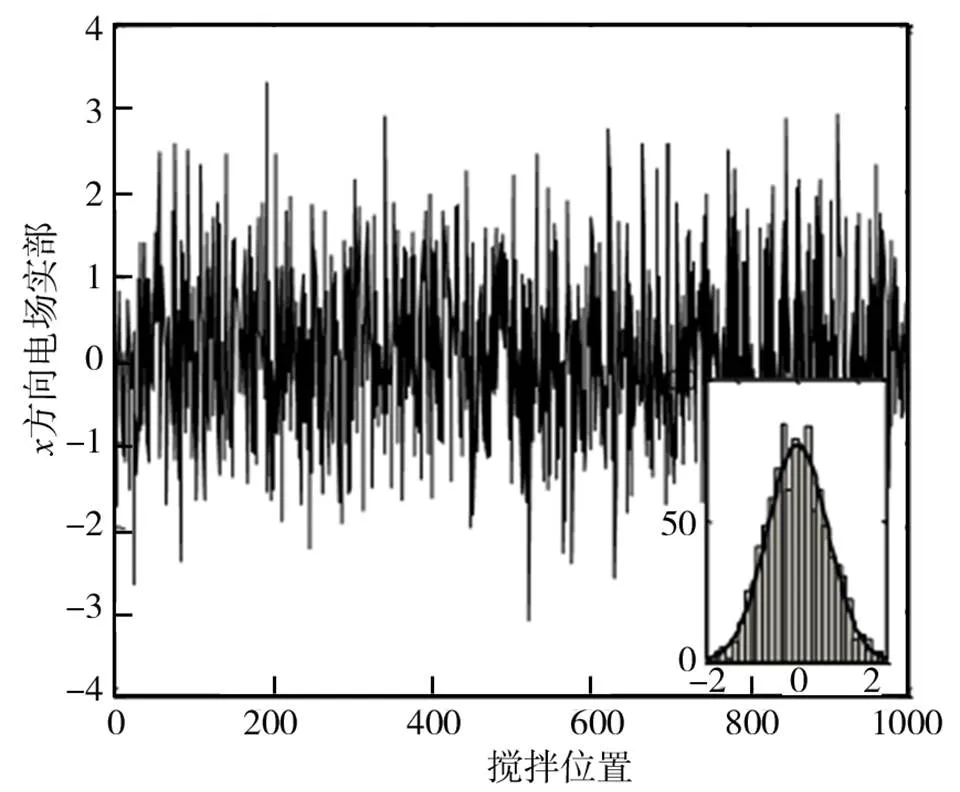
图3 仿真结果与理论混响室分布对比

2 BPSK系统干扰机理分析

为研究其干扰机理，以一个采用标准BPSK信号的数字通信系统为例。将干扰噪声AWGN作为激励信号，利用蒙特卡洛方法进行建模，形成混响室内全向辐照电磁环境。标准BPSK接收系统受到BPSK信号干扰时，接收信号模型可由式（1）给出：

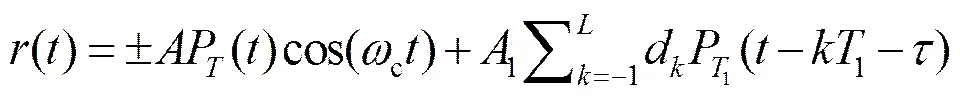
式中：为期望信号的幅度；1为干扰信号的幅度；c为期望的载波频率；为连续波干扰信号频率偏移量；为干扰信号的相位；P()为单位高度和持续时间为的矩形脉冲；为期望信号的码时间(1/)；1为干扰信号的码时间(1/1)；为位传输时间的偏移量，=min(,1)，0<1；d为干扰信号的数据码，d=±1；w()表示均值为0，方差为0/2的AWGN信号。

当干扰信号码速低于期望信号码速时，令期望信号码速为4800 B/s，信干比为10 dB，干扰信号相位服从区间[0, 2π]内的随机分布，不同干扰信号码速情况下，通信系统误码率随频率偏移的变化曲线，如图4所示。可以看出，当信干比相同时，在相同的频率偏移下，干扰信号的码速越高，其干扰效果越好。随着频率偏移量的增加，接收系统误码率也随之减小，且呈现周期性规律，即=/2，=1，3，5，7，…附近，不同码速的干扰信号的干扰效果相同。

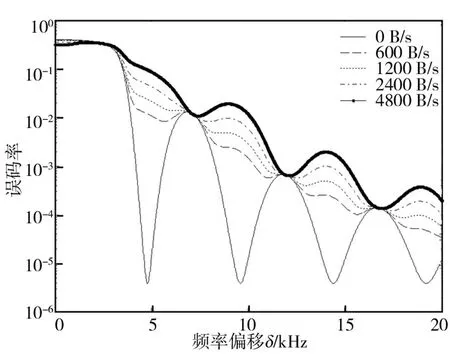
图4 不同干扰信号码速情况下，通信系统误码率随频率偏移的变化曲线

当干扰信号码速高于期望信号码速时，令干扰信号码速分别为4800，9600 B/s，计算了干扰信号与期望信号载频相同时，接收系统的误码率，并与连续波干扰的效果进行对比如图5所示。计算结果表明，当干扰信号与期望信号载频相同，干扰信号相位随机时，对于以上三种干扰信号，连续波干扰信号的干扰效果最好，且较低码速的干扰信号的干扰效果优于较高码速的干扰信号。通过进一步计算可知，随着干扰信号码速的进一步增大，干扰效果将呈现逐渐降低的趋势。

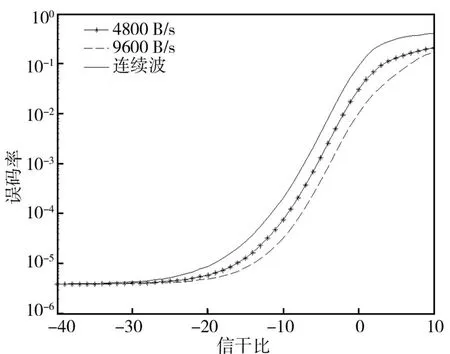
图 5 不同干扰信号码速情况下的理论误码率曲线

3 结语

对基于混响室原理的全向辐照电磁环境特点进行了分析，并利用蒙特卡洛法对其进行构建，通过对比分析可知所构建电磁环境符合混响室内电磁场分布特征。以一个采用标准BPSK信号的数字通信系统为例，研究干扰信号码速、频率偏移量、信干比等参数对系统误码率的影响，分析了干扰信号码速低于或高于期望信号码速时，干扰信号码速的变化和干扰效果之间不同的关系。研究结果在电子装备的复杂电磁环境适应性方面做出了有益探索，为今后的复杂电磁环境适应性理论的深入研究打下了基础。

[1] 贾锐, 王庆国, 王树峤, 等. 基于传输线原理的混响室散射场场线耦合模型[J]. 强激光与粒子束, 2014, 26(1): 222—226.

[2] HOLLOWAY C L, SHAH H A, PIRKL R J, et al. Reverberation Chamber Techniques for Determining the Radiation and Total Efficiency of Antennas[J]. Antennas Propag, 2012, 60(4): 1758—1770.

[3] 贾锐, 王庆国, 程二威, 等. 混响室“全向辐照”电磁环境场线耦合规律分析[J]. 电波科学学报, 2014, 29(2): 385—390.

[4] XU Ling-jun, WANG Qiang, WU Xiao-guang, et al. Adaptive Digital Predistorter for Radio Frequency Power Amplifier Linearization[C]// IEEE International Symposium on Microwave, Antenna, Propagation, and EMC Technologies for Wireless Communications. 2007.

[5] PATRICK R, SUK K M, DOMINIQUE C, et al. Frequency-selective Predistortion Linearization of RF Power Amplifiers[J]. Microwave Theory and Techniques, 2008, 56(1): 65—75.

[6] ANDRIES M I, BESNIER P, LEMOINE C. Estimating K-factor and Time Spread Parameters from a Transient Response of a Pulse Modulated Sine Wave in Reverberation Chamber[J]. Antennas and Propagation, 2013, 61(1): 380—389.

[7] ARTZ T, HIRSCH H. Pulsed Signals in Reverberation Chambers: Experimental Analysis of transient Peaks[C]// Proceedings of the Electromagnetic Compatibility (EMC EUROPE), International Symposium on Electromagnetic Compatibility, 2013.

[8] DAVID A H. Electromagnetic Fields in Cavities[M]. NewYork: Wiley-IEEE Press, 2009.

[9] KENT M, PAUL H, CHARLIE O. Models for the Number of Independent Samples in Reverberation Chamber Measurements with Mechanical, Frequency, and Combined Stirring[J]. IEEE Antennas and Wireless Propagation Letters, 2004, 3(1): 48—51.

[10] 王庆国, 贾锐, 程二威. 混响室连续搅拌工作模式下的辐射抗扰度测试研究[J]. 高电压技术, 2010, 36(12): 2954—2959.

[11] L-HDBK-237D, Electromagnetic Environmental Effects [S].

[12] ANTONIO S, GIUSEPPE F, MAURIZIO M. The Reverberation Chamber as Emulator of Radar Ground Clutter Doppler Spectra[C]// Proceedings of the Fourth European Conference on Antennas and Propagation. 2010.

[13] 王皓, 韩壮志, 何强, 等. 基于混响室的雷达杂波多普勒频谱模拟[J]. 现代雷达, 2013, 35(9): 69—72.

[14] 梁玉英, 涂鹏, 韩壮志, 等. 混响室雷达地杂波统计特性模拟[J]. 强激光与粒子束, 2015, 27(8): 159—163.

Structure of Full Radiation Electromagnetic Environment and Interference Mechanism of BPSK System

JIA Rui, WANG Chuan-chuan, ZHAO Lin-feng

(State Key Laboratory of Complex Electromagnetic Environment Effects on Electronics and Information System, Luoyang 471003, China)

Objective To analyze the complex electromagnetic environment of a communication station and build a full radiation electromagnetic environment based on the principle of live room. Methods A standard BPSK communication system was taken as an example to research the code rate of interference signal, frequency offset, and signal to interference ratio (SIR) on bite error rate (BER) of the system. Results The BER decreased with the increase of frequency offset and presented a periodicity rule, if the code rate of inference signal was lower than expectation. When the frequency offset was the same, the higher the code rate was, the better the interference effect was. If the code rate of interference signal was higher than the expectation, the interference affect decreased with the increase of the interference signal. Conclusion The study is a beneficial exploration on complex electromagnetic environment suitability of electronic equipment. It provides a foundation for in-depth research of complex electromagnetic environment suitability in the future..

full radiation; statistical property; BER, frequency offset, SIR

10.7643/ issn.1672-9242.2017.04.002

TJ01；TN97

A

1672-9242(2017)04-0005-04

2016-10-17；

2016-12-07

国家自然科学基金项目（51277180）

贾锐（1986—），男，博士，主要研究方向为电磁环境模拟及评估技术。