飞机结构表面涂层的热应力拓扑优化

王明庆

飞机结构表面涂层的热应力拓扑优化

王明庆

（中国商用飞机有限责任公司上海飞机设计研究院，上海201210）

飞机结构表面涂层与机体结构零件之间的热膨胀系数的失配引起的残余应力影响着涂层的机械和物理性能。使用拓扑优化方法设计涂层和零件之间适当的界面形式，使整个结构的总应变能达到最小。优化结果可为不同尺寸零件

的涂层设计提供参考。

飞机；表面涂层；热应力；拓扑优化

热应力是影响飞机结构表面涂层性能的一个重要因素。由于晶格常数的失配和热膨胀系数的失配，在涂层与结构界面处存在着残余应力。这些应力将导致涂层的裂纹、位错及其他类型的损伤，这些损伤对涂层的物理性能具有显著的影响。

飞机结构表面涂层与机体结构零件可以整体看作涂层/基底结构。目前已存在若干种减小涂层/基底结构中的残余应力的技术，如使用缓冲层、应变平衡法等。但是如果使用缓冲层，就必须引入另一种材料，这可能对整个结构的物理性质产生其他方面的影响。应变平衡法适合多层涂层问题，即具有两层以上涂层的结构，而对于双层结构则是无效的。

本文给出了另一种获得低应力涂层/基底结构的方法，即使用拓扑优化方法[1-4]来设计界面形式，使整个结构的总应变能最小化。该方法的优点在于其对涂层的层数和厚度没有限制，并且易于扩展以解决其他种类的残余应力问题。

1 理论推导

考虑图1中的涂层/基底结构，假设涂层和基底的材料分别为材料1和材料2，由于两种材料之间的热膨胀系数的失配，该结构中将存在热应力，这将导致裂纹、位错和其它损坏。为了减少应变能，可以重新设计界面处的材料分布。在该问题中，需假设顶层和底层分别固定为材料1和材料2，仅对界面附近的中间层的材料分布进行重新设计。

图1 涂层/基底结构的拓扑优化

为了进行优化过程，假设设计区域中的每个点都由材料1和材料2组成，并用x来表示材料1的体积分数，则（1-x）是材料2的体积分数。这种混合物的材料参数可以通过具有惩罚值的固体各向同性材料[1]给出，

其中，E是杨氏模量，α是热膨胀系数。在优化过程中，x可以具有0和1之间的任意值，即在设计区域中将存在灰色区域。但实际上想得到绝对的0-1分布，因为在实际结构中，每个点不是材料1就是材料2.为此，可以引入等式（1）和（2）中的惩罚值p和q.经验表明，如果选择p>3，通常可以得到0-1分布的优化设计。

使涂层/基底结构的热应变能最小化的公式可以写为[5]

其中，Ft是由热膨胀引起的力。Vmin和Vmax并且分别是材料1的最小体积分数和最大体积分数。Ft可以用离散形式表示为：

其中B是应变位移矩阵。总应变能Φ及其灵敏度分析可以推导如下

Φ还可以用以下等效形式表示：

其中εe=（ε-εt）是可以产生应力的弹性应变，ε=sym（▽u）是总应变，εt是由温度变化引起的应变。当使用目标函数（5）和（6）时，结果是相同的。因此在以下推导过程中只使用方程（5）作为目标函数。为了获得应变能Φ的灵敏度，使用平衡方程KU-Ft=0进行以下计算：

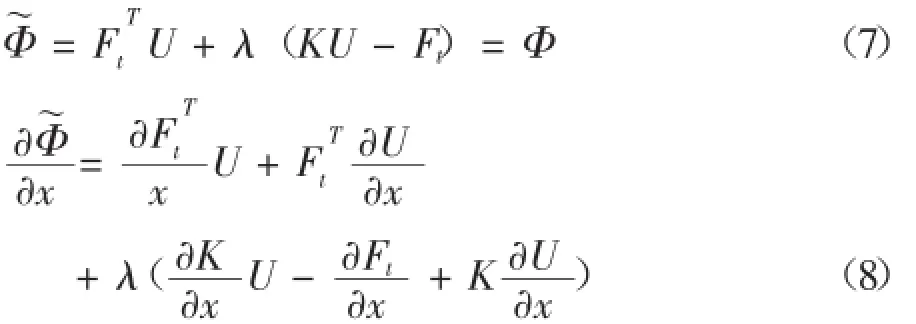
从而得到应变能的灵敏度为

2 数值计算

在本节中，给出一些示例，并尝试获得可以最小化飞机表面涂层结构的热应变能的设计。涂层和基底的厚度分别为1 mm和4.3 mm.涂层的直径是一个变量，以便将结果与涂层的厚度与直径的不同比率进行比较。

首先优化半径为20 mm的涂层。界面区域的初始密度设置为均匀分布。图2显示了优化设计的最终结果。可以看出，优化的界面在中心区域是一个平面，而在边缘处，涂层厚度逐渐增加，基底的厚度逐渐降低。该优化结构的总应变能比平直界面的结构减小了7%.

图2 直径20mm的优化结果

进一步的计算表明，如果增加涂层半径，边缘处的非平面面积将减小。当半径远大于厚度时，该区域可以忽略。图3是半径250 mm的涂层的优化结果。可以看到，在这种情况下，最优界面是一个平面。因此，当涂层厚度与半径相当时，可以得出结论，最佳界面不是平面。而当涂层厚度远小于半径时，最佳界面为平面。

图3 直径250mm的优化结果(p=3，q=1/4)

3 结论

本文使用拓扑优化算法分析了由热膨胀系数的失配引起热应变的涂层/基底结构。通过数值计算，发现如果涂层厚度远小于半径，最佳界面是一个平面。而如果厚度与半径相当，则最佳界面在中心区域是平面，而在边缘区域，涂层的厚度逐渐增加，而基底的厚度逐渐降低。该优化结果的意义在于，对于横向尺寸较小的零件（例如螺钉、销轴等），可按本文提供的方法进行端头外形的设计，以降低表面涂层的残余应力，增加涂层的整体性能及使用寿命。

[1]M.P.Bends e，O.Sigmund，Topology Optimization，Theory，Methods and Applications[M].Springer，2003.

[2]X.Guo，G.D.Cheng，Recent development in structural design and optimization[J].Acta Mechanica Sinica，2010，26（6）：807-823.

[3]M.P.Bendsφe，Optimal shape design as a material distrib ution problem[J].Structural Optimization，1989，1（4）：193-202.

[4]M.P.Bendsφe，O.Sigmund，Material interpolations intop ology optimization[J].Archive of Applied Mechanics，1999，69（9）：635-654.

[5]O.Sigmund，On the design of compliant mechanismsusing topology optimization[J].Mechanics Based Designof Struc tures and Machines，1997，25（4）：493-524.

Topology Optimization of Aircraft Surface Coating With Thermal Stress

WANG Ming-qing
（Shanghai Aircraft Design&Research Institute，Commercial Aircraft Corporation of China，Shanghai 201210，China）

The residual stress caused by the mismatch of thermal expansion coefficient between the surface coating and the structural parts of the aircraft affects the mechanical and physical properties of the coating. Topology optimization method is used to design the appropriate interface between the coating and the parts to minimize the total strain energy of the whole structure.The optimization results can provide reference for the coating design of different size parts.

aircraft；surface coating；thermal stress；topology optimization

O343.6

A

1672-545X（2017）02-0131-02

2016-11-23

王明庆（1985-），男，上海人，硕士研究生，工程师，主要从事飞行器结构设计工作。