自回归求和移动平均模型在湖北省戊型病毒性肝炎发病率预测中的应用

严 婧，杜玉开，杨北方

1)江汉大学医学院护理学系 武汉 430056 2)华中科技大学同济医学院公共卫生学院儿少卫生与妇幼保健学系 武汉 430030 3)湖北省疾病预防控制中心传染病防治所 武汉 430079

自回归求和移动平均模型在湖北省戊型病毒性肝炎发病率预测中的应用

严 婧1,2)，杜玉开2)，杨北方3)#

1)江汉大学医学院护理学系 武汉 430056 2)华中科技大学同济医学院公共卫生学院儿少卫生与妇幼保健学系 武汉 430030 3)湖北省疾病预防控制中心传染病防治所 武汉 430079

#通信作者，男，1979年2月生，博士，副主任医师，研究方向：疫苗针对疾病的预防和控制，E-mail：308041407@qq.com

戊型病毒性肝炎；自回归求和移动平均模型；发病率；预测；湖北省

目的：应用自回归求和移动平均模型(ARIMA模型)对湖北省戊型病毒性肝炎疫情报告数据进行分析、预测，为戊型病毒性肝炎的监测、预警提供理论依据。方法：采用SAS 9.2对2004年1月至2015年12月湖北省戊型病毒性肝炎的报告疫情数据进行ARIMA 模型的参数估计、拟合检验，预测2016年1月至12月戊型病毒性肝炎的月发病数，并用实际数据验证评估预测效果。结果：ARIMA(1,1,1)×(0,1,1)12模型拟合误差RMSE为0.045，2016年1月至12月戊型病毒性肝炎预测值平均相对误差为14.23%，能较好地拟合原始序列数据，预测精度较高。结论：ARIMA模型对湖北省戊型病毒性肝炎报告发病率短期预测精度良好，具有实际应用价值。

随着传染病预警系统的日渐完善，电子计算机技术的发展，多个领域的相互合作，各种数学预测模型越来越广泛地应用于传染病的预测，并得到国内外学者的一致认可[1-3]。有研究[4]在对12种不同的预测方法进行比较后提出自回归求和移动平均模型(autoregressive integrated moving average model，ARIMA模型)是最好的预测模型之一。ARIMA模型预测方法作为一种重要的时间序列分析方法被广泛地应用于各领域，近年来国内外学者[5-8]利用疫情监测资料构建ARIMA模型预测传染病的发病趋势，并取得了较好的预测效果，但尚无利用该模型对湖北省戊型病毒性肝炎发病趋势开展预测的文献报道。有鉴于此，该研究利用2004至2016年湖北省戊型病毒性肝炎的报告发病资料，采用ARIMA乘积季节模型对戊型病毒性肝炎的发病趋势进行了预测，以期为今后湖北省戊型病毒性肝炎的防控工作提供科学依据。

1 资料与方法

1.1 资料来源 数据资料来源于中国疾病预防控制信息系统，为2004年1月至2016年12月湖北省17个地(市、州)的戊型病毒性型肝炎报告发病个案资料。

1.2 ARIMA模型

1.2.1 基本原理 ARIMA方法以时间序列的自相关分析为基础，分析时间序列本身以及不同滞后期的自相关、偏自相关系数，即自相关函数(auto correlation function，ACF)和偏自相关函数(partial auto correlation function，PACF)，用于发现时间序列的特征。根据序列的不同特征以及选择参数的不同，该模型可分为：ARIMA(p，d，q)×(P，D，Q)s，ARIMA(p，d，q)，ARIMA(p，q)，AR(p)和MA(q)。根据序列是否与季节有关又可分为：季节模型ARIMA(P，D，Q)、非季节模型ARIMA(p，d，q)以及季节乘积模型ARIMA(p，d，q)×(P，D，Q)s。p，d，q以及P，D，Q分别表示非季节模型和季节模型中的自回归的阶、差分(季节差分)次数、滑动平均的阶。模型中参数的确定与自相关函数、偏自相关函数密切相关，ACF、PACF是判别序列适合于哪种模型建模的重要参考指标[9]。

1.2.2 建模过程[10-11]

①平稳性检验：平稳性检验是为了使序列减少随机变量的个数，增加待变量的样本容量，即简化时序分析的难度，提高对均值函数的估计精度。首先要对时间序列进行正态性检验，若不服从正态分布，要进行转化，一般包括自然对数转换和平方根转换，使转换后的数据服从正态分布，然后采用自相关分析、偏自相关分析及单位根检验(ADF检验)等方法来对时间序列的随机性、平稳性及季节性进行分析，而ADF检验为平稳性统计检验的最常用方法。如果序列为非平稳序列，必须采取相应的措施进行处理，如对数转换、差分运算使序列平稳化。

②模型识别：模型的识别过程即为序列定阶的过程，是ARIMA分析中关键的一步，其中基于样本ACF和PACF的性质的估计来对自回归阶数(p)和移动平均阶数(q)进行定阶。

③参数估计：根据以上各个参数的几何意义给出p、d、q、P、D、Q 的初始值后，ARIMA程序能够估计模型的参数，这里常常采用迭代计算法，以确定最大似然系数，并获得拟合值、预测值、误差(残差)以及可信区间。

④模型检验：残差序列的自相关函数和偏自相关函数不应与0有显著的差异，残差应随机，即白噪声。在各阶延迟下LB统计量的P值均>0.05，反映此拟合模型显著有效。

⑤模型的比较：用于比较各模型间拟合优度的统计指标包括确定系数(R2)、赤池信息准则(AIC)、贝叶斯信息准则(BIC)和残差平方和(RSS)。AIC适合自回归模型，而BIC是更为通用的标准，在判断模型优劣时，可将两者结合使用。

1.3 统计分析方法 该研究利用Excel 2007对湖北省戊型病毒性肝炎情资料进行整理，将2004年1月至2015年12月的戊型病毒性肝炎的发病数据作为建模部分，2016年1月至12月的发病数据作为模型验证部分，采用SAS 9.2对湖北省戊型病毒性肝炎不同年份发病率进行趋势χ2检验，建立ARIMA 模型，进行模型的参数估计、拟合检验和预测。

2 结果

2.1 2004至2016年湖北省戊型病毒性肝炎报告发病率的流行趋势 见图1。由图1可知，湖北省戊型病毒性肝炎报告发病率有明显的周期性以及趋势性，整体呈现上升的趋势，上升幅度较小，3～5月份发病率相对较高。

图1 2004至2016年湖北省戊型病毒性肝炎发病率的流行趋势

2.2 ARIMA模型的建立与预测

2.2.1 平稳性检验 通过观察原始时间序列图可以初步判断序列具有季节性，结合原始序列的ACF图(图2)可见，在时点12和24处都有一个局部的极大值，在这些时点处的序列值缓慢降低，这提示需进行季节差分来获得稳定的均值。

将原始序列进行一次差分和一次季节差分后(图3)，数据的线性趋势消失；同时对差分后的数据进行ADF检验，P<0.001，提示数据平稳。

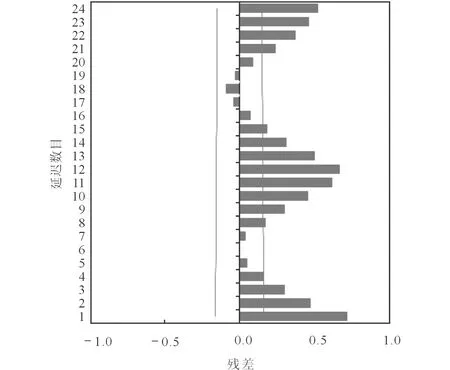
图2 原始序列的ACF图

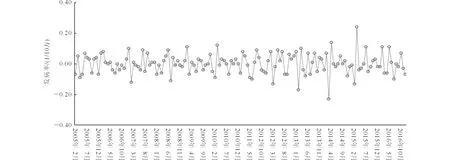
图3 原始序列经一次差分及一次季节差分转换后的序列图

2.2.2 ARIMA模型的识别 观察原始序列经一次差分和一次季节差分后的ACF和PACF(图4)，拖尾、截尾现象不明显，初步确定模型为复合季节模型ARIMA(p,1,q)(P,1,Q)12。

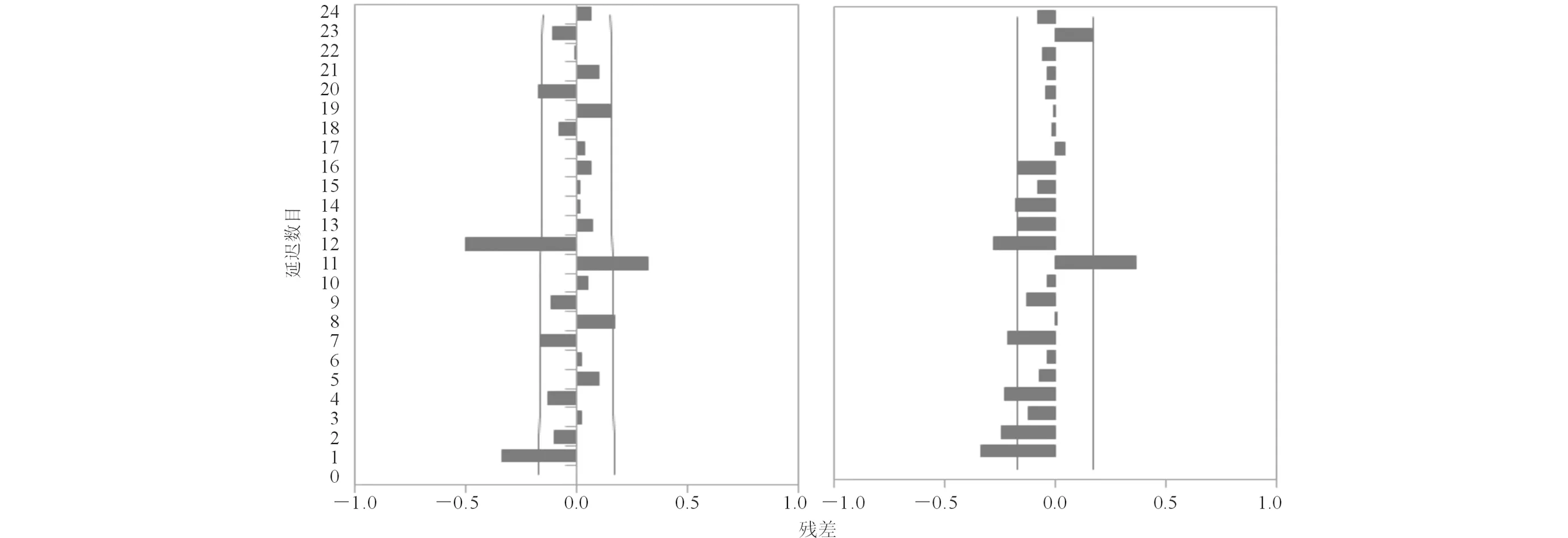
图4 原始序列经一次差分和一次季节差分后的ACF(左)和PACF(右)图

模型中p、P和q、Q四个参数采取从低阶到高阶逐个进行尝试以检验各个模型的拟合优度，并进行比较。选取其中拟合效果最好的几个模型，比较各个模型的拟合参数，初步选出拟合效果最好的ARIMA模型，如表1所示，ARIMA (1,1,1)×(0,1,1)12模型为最优模型。

表1 各个模型的拟合优度统计量

2.2.3 ARIMA模型的参数估计 对ARIMA (1,1,1)×(0,1,1)12模型进行参数估计，结果见表2，P<0.001，可见模型的各个参数均具有统计学意义。

表2 ARIMA (1,1,1)×(0,1,1)12 模型参数估计结果

2.2.4 模型检验 对该模型的残差序列进行白噪声检验，结果显示延迟6阶，延迟12阶，延迟18 阶，延迟 24 阶的LB检验统计量的P值均>0.05，说明残差为白噪声序列；残差序列的自相关函数和偏自相关函数如图5所示，ACF、PACF值均在置信区间内，提示序列为纯随机序列，说明ARIMA(1,1,1)×(0,1,1)12模型的拟合有效，初步确定其模型表达式为：(1-0.507B12)(1-B)(1-B12)Yt=(1-0.944B)(1-0.904B12)et。

图5 ARIMA (1,1,1)×(0,1,1)12模型残差序列的ACF(左)和PACF(右)图

2.2.5 模型预测 利用模型ARIMA (1,1,1)×(0,1,1)12预测湖北省2016年1月至12月的戊肝月发病率(1/10万)，预测结果如图6和表3所示，可见戊肝实际发病率都在ARIMA模型预测值的95%的置信区间内。经Ljung-Box检验[Q(15)=13.199,P=0.587]，表明残差已无滞后相关性，为白噪声序列。

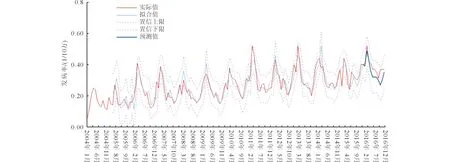
图6 ARIMA模型对2016年1～12月湖北省戊肝月发病率的预测情况

表3 ARIMA模型对2016年1～12月湖北省戊肝月发病率的预测值

3 讨论

发病率表示在一定期间内，一定人群中某病新发生的病例出现的频率[12]。发病率直接测定发病风险，是分析病因的重要依据，反映了疾病对人群健康的影响，同时可以用于评价防治措施的效果。对发病率进行预测是传染病控制工作的重要环节，科学的预测是正确决策的首要前提和条件，如果能够对传染病未来的流行趋势、变化规律及相关影响因素进行合理的预测，可及时发现疾病的暴发和流行，有的放矢地采取防控措施，对于传染病的预防和控制具有重要的意义[13]。此外，发病率预测具有十分重要的预警价值，若实际发病率在预测值的95%的置信区间内波动，即表明当月病毒性肝炎的疫情正常，否则就需要警惕病毒性肝炎的流行或暴发，可及时采取相关措施。

ARIMA模型是一种基于时间序列分析、预测和控制的定量预测方法，其根据对时间序列资料进行统计处理，找出系统内在统计特性及发展规律性，并将其进行外延，对未来进行预测[11]。它以时间综合代替各种影响因素，根据以往数据的特点建立模型，可消除时间序列的随机波动，拟合确定型趋势，其短期预测精度较高[5-6]。该研究利用2004年1月至2016年12月湖北省戊肝月报告发病率资料，采用ARIMA模型对戊肝的发病趋势预测，既能明确湖北省戊肝防控现状，又为下一步防控措施的制定提供科学依据。预测结果显示：ARIMA (1,1,1)×(0,1,1)12模型拟合误差RMSE=0.045，2016年1～12月预测值平均相对误差为14.23%，发病率预测结果的平均相对误差均在10%左右，能较好地拟合原始序列数据，预测精度较高。胡建利等[14]也曾构建ARIMA模型预测江苏省戊肝的月发病数，其结果也显示预测效果较好。

湖北省2004年至2016年戊型病毒性肝炎报告发病率呈上升的趋势，与福建省的报道基本一致[15]。戊肝报告发病率的逐年升高趋势，可能与人口流动日益频繁和农村卫生条件差使感染机会增多有关，应引起重视，进一步加强饮水卫生和食品安全的监管。鉴于ARIMA模型对戊肝报告发病率短期预测精度较高，具有一定实际应用价值，可作为戊肝防控工作中的辅助工具，监测戊肝疫情，为相关部门的卫生决策提供科学依据，同时还可将戊肝预测值95%CI作为戊肝暴发的阈值，为预警提供依据。该研究采用时间序列模型对戊型病毒性肝炎进行预测，能较好地分析传染病的周期性及季节性变化的规律，但只能分析线性资料，仅考虑时间这一影响因素，没有考虑到其他变量对发病率的影响，预测结果很大程度上受疫情报告资料质量的影响。此外，预测模型是建立在历史数据的基础上，建模前提是数据的外延，若外界影响因素突然变化，或是有新的变量引入，都会对模型的预测效果造成极大的影响，降低预测效能，因此需加强疫情监测系统的数据质量，提高网络直报数据的及时性和准确性，将新的变量纳入模型，使模型更具有代表性，提高预测精度。

[1]曲江文,聂绍发.传染病预测预警方法的研究进展[J].医学与社会,2014,27(10):13

[2]林玫,李永红,董柏青.传染病预测预警方法在我国的应用现状[J].中国热带医学,2010,10(3):308

[3]JIA ZW,CHENG SM,JIA XW.A mathematical model for evaluating tuberculosis screening strategies[J].J Evid Based Med,2011,4(1):48

[4]武红涛.ARIMA模型在医院出院患者预测中的应用[J].解放军医院管理杂志,2009,16(1):21

[5]陈莉.探讨ARIMA模型在细菌性痢疾发病预测中的应用[J].中国卫生统计,2011,28(4):417

[6]朱奕奕,冯玮,赵琦,等.ARIMA乘积季节模型在上海市甲肝发病预测中的应用[J].复旦学报(医学版),2012,39(5):460

[7]万燕丽,杨永利,施念,等.ARIMA模型在河南省 AIDS疫情预测中的应用[J].郑州大学学报(医学版),2015,50(2):160

[8]FIRMINO PR,DE MATTOS NETO PS,FERREIRA TA. Correcting and combining time series forecasters[J].Neural Netw,2014,50:1

[9]冯丹,韩晓娜,赵文娟,等.中国内地法定报告传染病预测和监测的ARIMA模型[J].疾病控制杂志,2007,11(2):140

[10]刘刚,唐宋,孙文杰.时间序列分析法在香港结核病预测中的应用[J].中国卫生统计,2012,29(2):226

[11]于林凤,吴静,周锁兰,等.ARIMA季节模型在我国丙肝发病预测中的应用[J].郑州大学学报(医学版),2014(3):344

[12]李立明.流行病学[M].北京:人民卫生出版社,2006.

[13]金连梅,杨维中.我国传染病预警工作研究现况分析[J].中国公共卫生,2008,24(7):845

[14]胡建利, 祖荣强, 彭志行,等.江苏省戊型肝炎发病趋势的时间序列模型应用[J]. 南京医科大学学报(自然科学版),2011,31(12):1874

[15]欧剑鸣,谢忠杭,洪荣涛,等.福建省2004-2010年戊型病毒性肝炎流行特征分析[J].中华流行病学杂志,2012,33(4):445

(2016-11-23收稿 责任编辑赵秋民)

Application of auto regressive integrated moving average model in forecasting incidence of hepatitis E in Hubei Province

YANJing1,2),DUYukai2),YANGBeifang3)

1)DepartmentofNursing,SchoolofMedicine,JianghanUniversity,Wuhan430056 2)DepartmentofChildandWomanHealth,SchoolofPublicHealth,TongjiMedicalCollege,HuazhongUniversityofScienceandTechnology,Wuhan430030 3)InstituteofInfectiousDiseaseControlandPrevention,HubeiCenterforDiseaseControlandPrevention,Wuhan430079

hepatitis E；auto regressive integrated moving average model；incidence；prediction；Hubei Province

Aim: To apply auto regressive integrated moving average model(ARIMA) to predict hepatitis E(HEV) incidence in Hubei Province, and provide the theoretical basis for future prevention strategies. Methods: Based on the reported HEV monthly incidence from January 2004 to December 2015 in Hubei Province, ARIMA model was applied to forecast the HEV monthly incidence in January to December 2016 using SAS 9.2,and the forecasted results were verified by the actual data of 2016. Results: The best model was ARIMA (1,1,1)×(0,1,1)12, the RMSE of this model was 0.045, and the average relative error of prediction was 14.23% with high precision.Conclusion: The ARIMA model can be used to forecast the HEV monthly incidence with high precision in the short-term in Hubei Province.

10.13705/j.issn.1671-6825.2017.03.012

R512.6