提高强冲击荷载作用下平板式防护门门框墙抗力的方法*
2017-06-07赵跃堂董晓鹏易义君
赵跃堂,董晓鹏,易义君,储 程
(中国人民解放军理工大学爆炸冲击防灾减灾国家重点实验室,江苏 南京 210007)
提高强冲击荷载作用下平板式防护门门框墙抗力的方法*
赵跃堂,董晓鹏,易义君,储 程
(中国人民解放军理工大学爆炸冲击防灾减灾国家重点实验室,江苏 南京 210007)
在强冲击波荷载作用下门框墙转角处会产生明显的应力集中,影响门框墙体系甚至整个防护结构的安全。为解决该问题,提出在迎爆面门框墙和衬砌结合部位设置薄弱层的构造方法,从而减小冲击荷载引起的过大的拉应力。运用考虑了剪切变形的悬臂梁理论分析表明,梁端部约束刚度的变化可以影响结构的破坏形态以及结构的内力分布,降低端部的约束刚度可以有效降低端部区域的内力峰值,延缓结构发生破坏的时间。利用有限元模拟的方法,分析了在出入口门框墙位置设置薄弱层对门框墙动力响应和破坏规律的影响。分析结果表明,设置薄弱层可以有效降低门框墙转角处的应力,降低门框墙结构破坏的风险,进而提高门框墙的抗力水平。
门框墙;强冲击荷载;薄弱层;动力响应

图1 薄弱层设置示意图Fig.1 Schematic diagram of weak layer
国防工程中防护门和门框墙是出入口最重要的设备,是地下防护结构的第一道屏障,在保护整个结构和内部人员安全方面有着举足轻重的地位,必须保证其具有足够的强度来抵御冲击波对结构内部的破坏[1-2]。在冲击荷载作用下,防护门的门框墙要同时承受门扇和冲击波荷载的双重作用,相比工厂预制的防护门门扇,现场浇筑的门框墙结构很有可能先于门扇发生破坏。因此,研究门框墙在强冲击荷载下的动力响应对保护整个防护结构有重要意义。
围绕门框墙问题,王有熙等[3]采用有限元方法,对门框墙结构模型和悬臂板结构模型进行了数值模拟,并与规范规定的方法进行比较,发现规范设计方法偏于保守;杨宜民[4]利用深梁和经典梁理论,充分考虑门扇和门框的共同作用,导出了梁式防护门、框体系的频率方程和振型函数;郭乙木等[5]对承受冲击荷载的防护门门框结构进行了平面实验模型的静力和动力分析以及门框墙整体结构的三维动力响应分析,给出了门框墙的破坏机理及动力参数的分布规律。目前多数门框墙的研究主要针对的是一般动力荷载,但是对门框墙抗爆和减爆措施研究较少,尤其是承受强冲击波荷载作用的地下坑道防护工程。
实际工程中,防护门的门框墙通过嵌入衬砌和围岩中来提高其嵌固刚度,从而使门框墙的整体抗力得到增强,如图1(a)所示,但并不是约束程度越高,结构的承载能力越强。因为爆炸荷载作用于整个坑道,门框墙体系和衬砌均会受荷载的作用,并在荷载作用下分别沿坑道轴向和径向运动,如果迎爆面上门框墙与衬砌的相互约束作用较强,势必导致该区域产生明显的应力集中,并在该位置首先发生破坏。对于厚跨比较大的门框墙,应力集中更明显,主要是端部发生剪切破坏,荷载较大时甚至发生直剪破坏,此时嵌固刚度的增加势必会加剧嵌固区域的剪切破坏,而不利于提高结构的承载力。因此,在满足门框墙使用要求的前提下,合理配置嵌固区域的嵌固刚度以提高结构整体的抗冲击性能。
合理配置门框墙嵌固区域的嵌固刚度,在工程上可以通过在门框墙迎爆面和衬砌交界处设置一定深度的薄弱层来实现,如图1(b)所示。下面通过理论分析和有限元计算,分析设置薄弱层前后门框墙的动力响应变化,进而研究不同深度的薄弱层对门框墙结构响应的影响。
1 冲击荷载下的动力响应
防护工程中,一般将门框墙划分为侧墙、上挡墙和门槛等部分,并按照牛腿或悬臂梁进行设计[6]。对于厚跨比较大的门框墙体系,在强冲击荷载作用下,在门框墙与衬砌的交界处发生的是弯剪,甚至直剪破坏,在迎爆面设置薄弱层可以降低周围介质对门框墙的约束刚度。综合上述考虑,采用基于Timoshenko梁理论的悬臂梁模型来考察端部内力在不同约束刚度下的变化,该理论能模拟厚跨比较大的梁的弯曲变形、弯剪变形和直剪变形[7-10]。
假定动载作用下梁破坏时的判定方法与静载下的相同,即当梁的内力达到钢筋混凝土的极限强度时就认定其破坏。考虑是动载作用,将冲击荷载作用下梁的极限弯矩和剪力定义如下:
(1)
式中:Mmax和Vmax分别为静载下梁的极限弯矩和剪力;Ω为由动载引起的强度增强因数,取Ω=1.6,与材料的应变率相关。有:
(2)
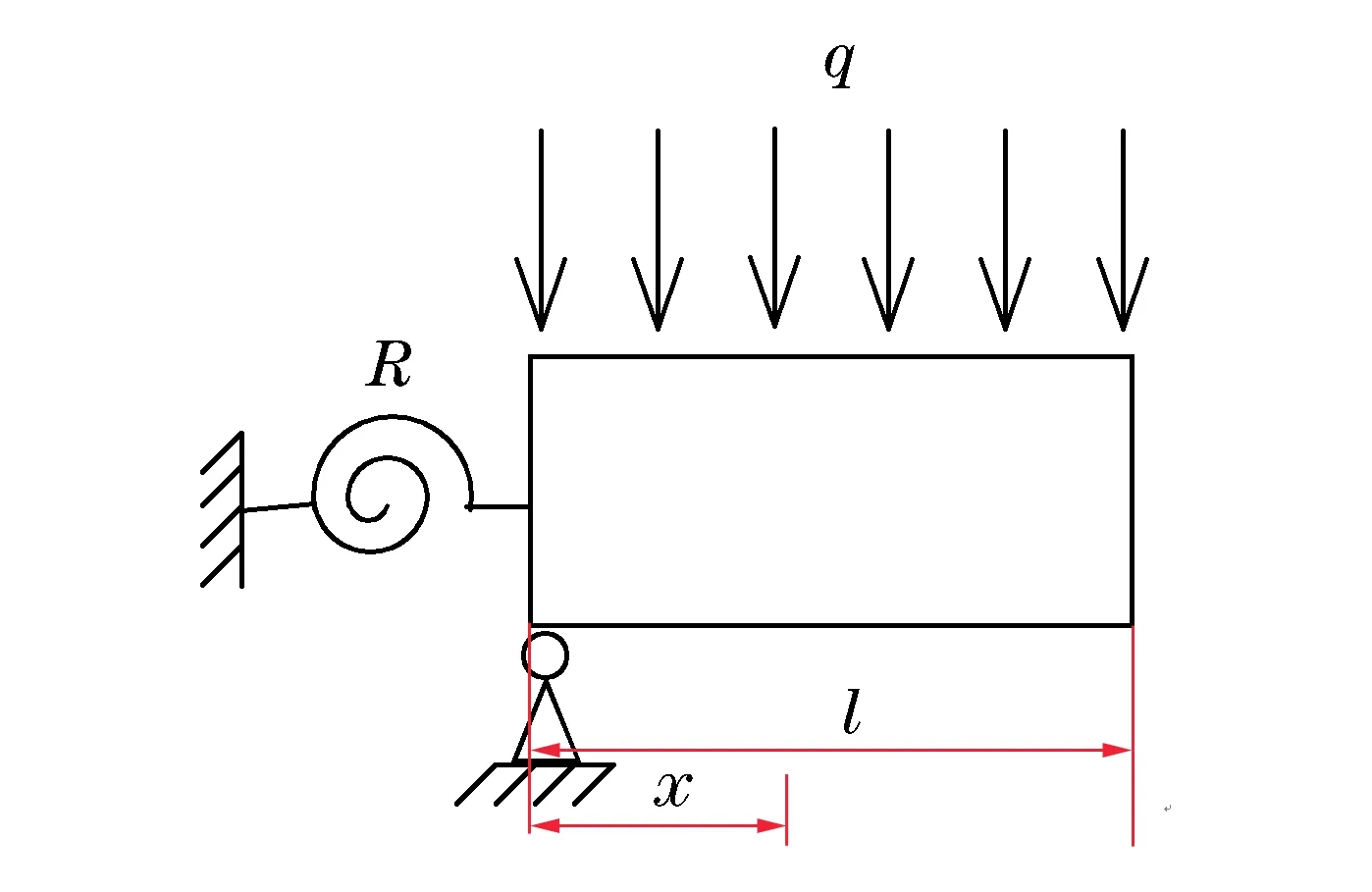
图2 悬臂梁模型Fig.2 The model for the deep cantilever beam
式中:fc为混凝土的抗压强度,fy为钢筋的抗拉强度,ρs为截面的配筋率,b为梁宽,h和h′分别为梁高和有效高度,As为钢筋的截面积。
悬臂梁分析模型如图2所示:R为梁端的嵌固刚度,受薄弱层深度的影响;q为作用于悬臂梁上的荷载,x为与梁端的距离,l为梁长。
悬臂梁内力与变形的关系为:
(3)

强迫振动方程为:
(4)
式中:r2=I/A,ρ为梁的密度。
边界条件为:
(5)
初始条件为:
(6)
对方程(4)可以采用振型分解法进行求解,令:
(7)
而外荷载q可以展开表示为:
(8)
Φn和Yn为振型函数,振型满足正交条件:
(9)
根据初始条件和边界条件,可以得到梁中的弯矩和剪力为:
(10)
爆炸荷载升压时间很短,可以近似为三角形荷载,表达式为:
式中:td为正压时间,p0为峰值压力。
正常情况下,门框墙是嵌固在围岩中并与衬砌浇筑在一起。从图1可以看出,门框墙的约束主要来自迎爆面、背爆面和侧面3个方向。工程上在迎爆面设置薄弱层,将直接减小迎爆面衬砌对门框墙端部的转动约束,同时也降低了衬砌的径向运动对门框墙的影响。为了比较约束刚度变化对悬臂梁动力响应的影响,选取4组不同的约束刚度R=,2EI,EI,0.5EI进行比较(EI是梁的弯曲刚度)。梁的几何尺寸l×h=0.57 m×0.36 m,有效高度为0.34 m,梁宽取单位1,配筋率为0.012,密度为2.4 t/m3,剪切模量为13.8 GPa,泊松比为0.2;混凝土的抗压强度为48.265 MPa,钢筋的抗拉强度为482.65 MPa;荷载峰值p0=34.5 MPa,荷载持续时间为1 ms。将上述参数代入公式(10)得到梁端的内力变化情况并绘成图3。

图3 强冲击荷载下不同约束刚度对梁端剪力和弯矩的影响Fig.3 Influence of different restraint stiffness on the shear force and bending moment of the beam end
图3是不同约束刚度下梁端部剪力和弯矩的变化图,纵坐标为梁端内力与冲击荷载下极限内力的比值,当比值V/Vu=1或者M/Mu=1时就认为梁端部达到了极限承载状态。从图3可以看出,随着梁端部约束刚度的降低,梁端内力会随之减小,且内力的增长速度变缓。比较图3(a)和图3(b)可以发现,发生剪切破坏的时间要先于弯曲破坏的时间,也就是说在荷载较大时,端部发生的是剪切破坏。将发生剪切破坏时,不同约束刚度情况下端部的弯矩绘成表1,表中ts为发生剪切破坏的时刻,Ms/M为发生剪切破坏时的弯矩与梁的弯曲承载力的比值。从表1可以看出,随着约束刚度的降低,梁端部发生剪切破坏的时间向后推迟,与R=的情况相比,其他几种情况的弯矩稍有增加,说明弯曲变形吸收的能量增多。所以,设置薄弱层可以明显改善端部的内力状态,提高端部的抗力。
综合上述分析可以发现,将门框墙简化为悬臂梁可以从宏观上描述约束刚度对梁端内力的影响,但是考虑到Timoshenko梁理论和实际工况之间的差异(包括几何差异和配筋条件等)以及破坏问题分析的复杂性,迎爆面设置薄弱层对门框墙体系不同位置的内力及破坏情况的影响还不清楚,下面将采用有限元方法对门框墙结构进行进一步分析。

表1 剪切破坏时的弯矩情况
2 设置薄弱层的有限元分析
2.1 有限元计算
2.1.1 模型简介

图4 结构和钢筋的有限元模型Fig.4 Finite element models for doorframe wall and reinforcing bar
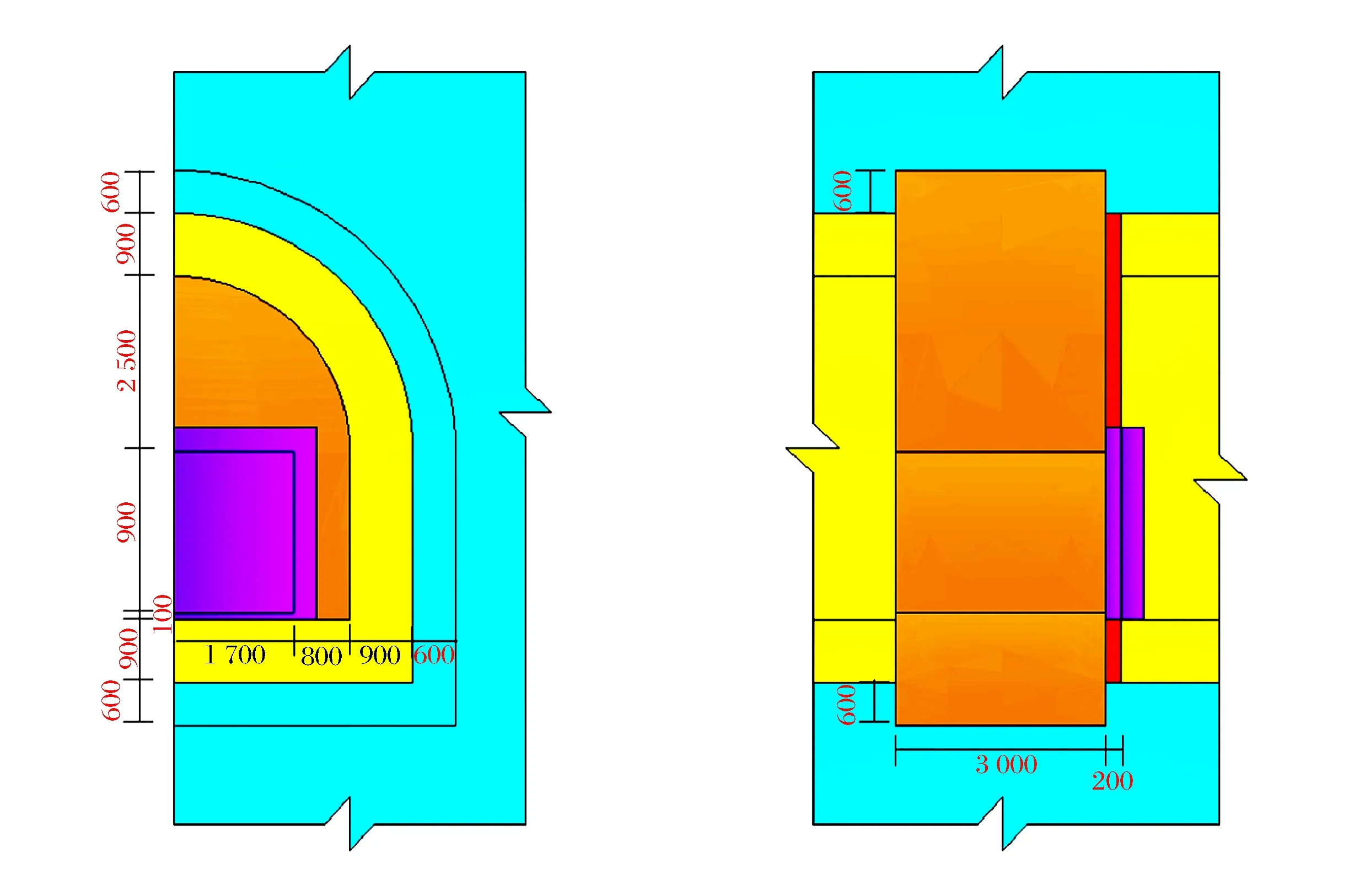
图5 门框墙及衬砌的尺寸Fig.5 The sizes of the doorframe wall and lining
计算采用LS-DYNA软件进行。根据结构对称性,取一半结构进行有限元建模以减少计算量。对于地下隧道,开挖仅在其周围距离坑道中心点3~5倍跨宽或高度的范围内有实际影响[11-12]。模型中衬砌边缘距中心点3.4 m,又考虑到在强冲击波作用下,应力响应范围较大,为减小边界对结构的影响,模型尺寸取为X方向(跨度方向)宽18 m,Z方向(垂直方向)高30 m,Y方向(洞室轴向)长21 m。模型均为八节点实体六面体单元,共包含1 572 647个单元,其中混凝土和围岩共有1 502 527个单元,钢筋包含70 120个单元。整个模型主要由门框墙、防护门、衬砌和围岩组成,门框墙与衬砌之间设置了一道薄弱层,深度贯穿衬砌,厚度为20 cm。整体模型如图4所示,各部分尺寸设置如图5所示。
岩体为III类围岩,混凝土和钢筋的材料参数取自文献[13]。有限元模型中围岩采用PSEUDO_TENSOR模型,为了设置无反射边界条件,模型边界处薄层采用经典的PLASTIC_KINEMATIC材料模型(LS-DYNA中其他材料模型对无反射边界条件的适用性较差),混凝土采用JOHNSON_HOLMQUIST_ CONCRETE材料模型,该模型适用于承受有大位移、大应变、高应变率的混凝土结构,钢筋采用考虑了应变率效应的PLASTIC_KINEMATIC塑性随动强化模型,钢筋采用HRB400,直径为25 mm,通过关键字CONSTRAINED_LAGRANGE_IN_SOLID来考虑钢筋与衬砌以及门框墙之间的粘结滑移。将防护门区域的荷载简化为三角形均布荷载[14],荷载峰值为15 MPa,荷载作用时间取0.3 s,荷载作用于防护门框体系和迎爆面的衬砌上。
2.1.2 边界设置

图6 边界设置Fig.6 The setting of the boundry
强冲击荷载作用下门框墙结构动力响应及破坏问题需要考虑2种荷载的作用:正常维护状态下,仅有初始静荷载作用,爆炸条件下还要叠加空气冲击波荷载的作用,另外,坑道内冲击波荷载作用到衬砌围岩上还要向外传播而不能从边界反射回来,因此该模型的边界条件需要综合考虑静荷载和动荷载作用和无反射边界条件设置。赵跃堂等[15]给出了该类型边界条件的处理方法。具体计算过程分2步进行:第1阶段是模拟静力作用,第2阶段是在第1阶段基础上叠加动力作用。具体的计算模型边界设置如图6所示,图中标记“0”表示仅静力计算时施加,标记“1”表示仅动力计算时施加,标记“0,1”表示静力和动力计算时都施加。
实际计算时,图6中上覆压力根据上面覆盖层厚度计算求出,在后面的动力计算时不变,图6下表面的法向约束边界条件需要置换成法向反力边界条件,因为约束边界条件限制了下表面的运动,从坑道内壁传播过来的地冲击波在固定边界会反射回去。而透射边界不能约束位移,所以需将原先的位移约束通过添加等效法向反力的方法来保持结构的平衡。

图7 门框墙的塑性应变Fig.7 The plastic strain of the doorframe wall
2.2 模拟结果分析
2.2.1 门框墙的塑性变化规律
图7展示了冲击荷载作用下门框墙的塑性应变,从图7可以直观看出:设置薄弱层以前,在强冲击荷载作用下,迎爆面结构的塑性应变区较明显,主要分布在门框墙与衬砌交界处和门框墙截面发生变化的地方,但是在背爆面,结构除部分区域产生塑性应变外,其他位置并没有产生塑性区;设置薄弱层以后,迎爆面上门框墙转角处、与衬砌的交界处的塑性应变区明显减小,背爆面上除对称面处塑性区稍有增大外,其余位置塑性应变基本不变。
2.2.2 衬砌的塑性应变规律
图8展示了衬砌上的塑性应变。从图8可以看出,门框墙外部的衬砌受到荷载的直接作用,这部分的塑性应变区较明显,其中衬砌与门框墙的交界、衬砌底部的转角两处的应变最大;背爆面只有很小一部分进入塑性状态。设置薄弱层以后,在薄弱层的位置上塑性应变增加明显,背爆面的塑性区稍有减小,其他位置变化不大。

图8 衬砌的塑性应变Fig.8 The plastic strain of the lining
2.2.3 塑性应变的数值变化

图9 单元的编号Fig.9 The number of the elements
从塑性应变图只能从宏观上看出不同位置塑性区的变化和发展情况,为了更精确地研究结构的破坏特征,分别在门框墙和衬砌上的关键位置上选取部分单元进行比较,其位置和编号如图9所示。
表2给出了门框墙上部分单元的塑性应变,表中εd,before为未设置薄弱层前的塑性应变,εd,after为设置薄弱层后的塑性应变。对比表4中的数据可以发现,设置薄弱层以后,在门框墙与衬砌交界处的单元塑性应变明显减小,降低为原来的10%以下;在门框墙截面发生突变的位置上,单元6和7的塑性应变也有明显降低;在塑性应变集中的单元3和9,塑性应变基本不变,值得注意的是位于背爆面上的单元9的塑性还稍有降低。这表明薄弱层不仅可以明显改善门框墙迎爆面上的应力情况,而且不会对背爆面造成不利影响,对受到冲击荷载作用的门框墙结构起到很好的保护作用。

表2 门框墙上单元的最大有效塑性应变
表3为衬砌上单元的塑性应变,其中单元10~14位于薄弱层的位置,单元15位于背爆面的衬砌上,表中εl,before为未设置薄弱层前的塑性应变,εl,after为设置薄弱层后的塑性应变。从表3可以看出:迎爆面薄弱层处单元的塑性应变增加明显,基本增大到原来的2倍;而位于背爆面衬砌上的单元15,塑性应变却减小。这表明,薄弱层通过变形的增加吸收了一定程度的荷载能量,同时断开了衬砌和门框墙的连接,使两者的相互作用力得到减弱,而且薄弱层位于门框墙外部,塑性应变增加并不影响内部人员和设备安全。

表3 衬砌上单元的最大有效塑性应变
2.2.4 结构位移响应
为了保证防护门在受到冲击荷载作用后依然能够正常开启,要求门框墙不能产生过大的相对位移,因此必须对门框墙的位移进行控制。在门框墙上取部分单元将其Y方向的位移绘成图10,从图中可以看出,位于门框墙对称面上单元8的位移最大,其次是位于门框墙中间位置的单元3,位移最小的单元5位于下侧位置。设置薄弱层以后,门框墙的整体位移增大,但是单元间的相对位移变化不大,也就是说门框墙体系在受到爆炸冲击以后防护门依然能够满足开启要求。
在衬砌上距离门框墙不同距离处选取部分单元(与单元12在同一高度上),将其沿荷载方向的峰值位移绘成图11。从图11可以看出,衬砌的整体位移增加,特别是设置成薄弱层的位置单元位移明显增加,但是其他位置处相对位移基本不变。

图10 门框墙单元Y方向位移Fig.10 Y-directional displacement-time curves of doorframe wall elements

图11 距离门框墙不同距离处衬砌单元的径向位移Fig.11 Radial displacements of lining elements with different distances away from the doorframe wall
2.3 薄弱层深度的影响
以上分析中,衬砌与门框墙完全断开,薄弱层是贯穿衬砌延伸到围岩中的。从分析结果可以发现,迎爆面上设置薄弱层对改善门框墙的受力性能具有很明显的作用。为了验证这种薄弱层深度是否为最优,另外将薄弱层延伸进入衬砌的深度设为300和600 mm,并取门框墙上的单元塑性应变进行比较,如表4所示。

表4 薄弱层深度对门框墙上单元塑性的影响
对比表4中的4组数据可以发现:随着薄弱层深度的增加,迎爆面门框墙上的塑性应变εd会显著减小,各个单元塑性应变也趋于均匀;背爆面的塑性应变虽然变化不大,但是也有减小的趋势。
上面分析表明,在满足工程密闭条件下,薄弱层设置的适宜深度是迎爆面门框墙和周围衬砌完全断开(中间可以填充柔性材料)。这很容易理解,强冲击波荷载作用区域包括门框墙和周围衬砌,两者在冲击波荷载作用下共同变形和运动,如图12所示,如果门框墙和衬砌完全断开,衬砌将沿门框墙表面“滑动”,此时接触区域的位移增大,但是内力减小。如果两者完全浇筑在一起,它们的接触刚度变大,衬砌类似于悬臂结构,接触区域的内力将显著增大,破坏程度也随之增大。

图12 结构运动趋势Fig.12 The relative motion trend of the structure
3 结 论
提出了在迎爆面门框墙与衬砌交界处设置薄弱层的方法,来提高门框墙的抗力水平。然后以考虑剪切变形的悬臂梁理论为基础,采用有限元模拟的方法进行了分析,并得出以下结论:
(1)门框墙上截面发生变化的转角和交界处,结构响应较大,在强冲击荷载作用下,会产生较大的塑性变形,最后发生剪切甚至是直剪破坏。
(2)迎爆面上设置薄弱层对门框墙体系是有利的。薄弱层不仅可以利用自身变形的增加削减一部分荷载能量,而且减弱了门框墙与衬砌的约束刚度,降低了迎爆面交界处的应力水平,同时又不会对背爆面产生不利影响。
(3)薄弱层设置的适宜深度是迎爆面门框墙和周围衬砌完全断开,此时门框墙和衬砌接触区域的破坏程度最小。
综上所述,在满足工程可靠性的前提下,合理设置薄弱层可以有效地改善强冲击荷载作用下门框墙的受力情况,提高门框墙的抗力水平。
[1] 方秦,柳锦春.地下防护结构[M].北京:中国水利水电出版社,2010:294-297.
[2] Crawford R E, Higgins C J, Bultmann E H. The air force manual for design and analysis of hardened structures[M]. New Mexico: Civil Nuclear System Corporation, 1980:523-529.
[3] 王有熙,许宏发,孙远.门框墙内力计算模型的比较分析[J].防灾减灾工程学报,2006,26(1):89-92. Wang Youxi, Xu Hongfa, Sun Yuan. Comparative analysis of the calculation models of doorframe wall’s internal forces[J]. Journal of Disaster Prevention and Mitigation Engineering, 2006,26(1):89-92.
[4] 杨宜民.防护工程口部梁式门、框体系动力性能研究[J].浙江大学学报(自然科学版),1992(增):96-106. Yang Yimin. Dynamic properties of beam-type doorframe wall system at the hardened entrance[J]. Journal of Zhejiang University (Natural Science), 1992(suppl):96-106.
[5] 郭乙木,鲁祖统.超强冲击波作用下地下坑道防护门门框结构设计的应用研究[J].浙江大学学报(自然科学版),1995,29(3):282-289. Guo Yimu, Lu Zutong. The practical study of protective doorframe structural design of a tunnel under super strong shock wave[J]. Journal of Zhejiang University (Natural Science), 1995,29(3):282-289.
[6] 中国建筑标准设计研究院.人民防空地下室设计规范:GB50038-2005.[S].北京:中华人民共和国建筑部,2005:73-76.
[7] Ross T J. Direct shear failure in reinforced concrete beams under impulsive loading: AFWL-TR_83_84[R]. Air Force Weapons Laboratory, Kirtland Air Force Base, NM, 1983:20-89.
[8] 钱七虎,王明洋.高等防护结构计算理论[M].南京:江苏科学技术出版社,2009:192-206.
[9] 柳锦春,方秦.爆炸荷载作用下钢筋混凝土梁的动力响应及破坏形态分析[J].爆炸与冲击,2003,23(1):25-30. Liu Jinchun, Fang Qin. Analysis of dynamic responses and failure modesof R/C beams under blast loading[J]. Explosion and Shock Waves, 2003,23(1):24-30.
[10] 方秦,吴平安.爆炸荷载作用下影响 RC 梁破坏形态的主要因素分析[J].计算力学学报,2003,20(1):39-42. Fang Qin, Wu Ping’an. Main factors affecting failure modes of blast loaded R/C beams[J].Chinese Journal of Computational Mechanic, 2003,20(1):39-42.
[11] 孙钧,汪炳鉴.地下结构有限元法解析[M].上海:同济大学出版社,1988:205-209.
[12] 丁泰山.超欠挖状态下地下洞室围岩稳定性数值分析[D].西安:西北工业大学,2007:18-20.
[13] Livermore Software Technology Corporation. 970 keyword user’s manual[M]. Livermore: Livermore Software Technology Corporation, 2003:92-99.
[14] Brode H L. Weapons effects for protective design[R]. California: Rand Corporation, 1960:17-20.
[15] 赵跃堂,罗中兴,李振慧,等.深埋地下结构静动力耦合响应分析的边界条件设置方法[J].岩土力学,2013,34(5):1495-1500. Zhao Yuetang, Luo Zhongxing, Li Zhenhui, et al. Boundary condition setting method for coupled static and dynamic response analysis of deep underground structure[J]. Rock and Soil Mechanics, 2003,34(5):1495-1500.
(责任编辑 张凌云)
Measures for improving the resistance of a flatbed protective doorframe wall under intensive shock loading
Zhao Yuetang, Dong Xiaopeng, Yi Yijun, Chu Cheng
(StateKeyLaboratoryofDisasterPreventionandMitigationofExplosionandImpact,PLAUniversityofScienceandTechnology,Nanjing210007,Jiangsu,China)
Intensive shock loading can lead to obvious stress concentration at the corner of a doorframe and jeopardize the safety of a doorframe wall and even the whole protective structure where it is installed. To solve this problem, we proposed to install a weak layer between the doorframe and the lining to reduce the excessive tensile stress, based on the cantilever beam theory that takes into account the shear deformation. The results show that, as the constraint stiffness of the beam end can influence the structure’s failure mode and distribution of the internal force, lowering the constraint stiffness of the beam end can reduce the peak value of the internal force and delay the failure time of the structure. Using the finite element method, we analyzed the influence of the weak layer on the dynamic response and the failure mode of the doorframe. The results show that the weak layer can effectively reduce the stress of the doorframe’s corner and the damaging effect of the doorframe wall structure so that the resistance of the doorframe can be improved.
doorframe wall; high impact load; weak layer; dynamic response
10.11883/1001-1455(2017)03-0487-09
2015-09-28;
2016-03-13
国家自然科学基金项目(51478469)
赵跃堂(1967— ),男,博士,教授,博士生导师; 通信作者: 董晓鹏,dxp0112@163.com。
O383.2 国标学科代码: 13035
A
