基于细观混凝土模型的刚性弹体正侵彻弹道偏转分析*

邓勇军，陈小伟，姚 勇，杨 涛

(1.西南科技大学土木工程与建筑学院，四川 绵阳 621000；2.中国工程物理研究院总体工程研究所，四川 绵阳 621999)

基于细观混凝土模型的刚性弹体正侵彻弹道偏转分析*

邓勇军1,2，陈小伟1,2，姚 勇1，杨 涛1

(1.西南科技大学土木工程与建筑学院，四川 绵阳 621000；2.中国工程物理研究院总体工程研究所，四川 绵阳 621999)

为研究混凝土细观因素对刚性弹正侵彻弹道偏转的影响，基于骨料随机投放的思路建立混凝土三维细观几何模型，分析刚性弹正侵彻过程中发生弹道偏转的原因及可能影响因素，定量讨论混凝土细观因素对弹道偏转的影响。结果表明：混凝土细观数值模型可以较好地反映弹体正侵彻过程中弹道偏转等典型物理现象，且细观参数对于弹体弹道偏转有显著影响。刚性弹正侵彻细观混凝土时，存在一个弹体直径/骨料最大粒径比的特征比值。

混凝土;细观建模;刚性弹;正侵彻;弹道偏转

混凝土材料由于其抗压强度较高、原料丰富及耐久性好等特点，被广泛应用于高坝、桥梁、核电站、机场跑道、公路及其他防护工程等重要基础设施建设。该类结构在使用过程中，除受常见的静力荷载、地震作用，在战争或恐怖袭击中还可能遭受弹体的侵彻爆炸作用。

侵彻过程是一个弹/靶相互作用的瞬态接触问题，目前在弹/靶侵彻理论、数值计算、实验等方面已做了大量研究，对混凝土靶侵彻问题已有较深刻认识[1-8]。已有文献中大多将混凝土视作均匀材料，无法考虑混凝土组成成分对侵彻过程的影响。一般而言，混凝土是典型的多相非均质复合材料，主要由粗骨料、水泥水化物及骨料与水泥砂浆粘结带等组成[9]，各相材料性质差异较大。即使是严格的刚性弹正侵彻，由于混凝土随机因素作用，弹体可能受到非对称力作用从而发生弹道偏转。若计算中将混凝土当作均匀材料分析，无法反映侵彻过程中弹体与骨料/砂浆的相互作用，以及弹体弯曲破坏、弹道偏转等典型的物理现象[10]。计算机性能的提高,使得从混凝土细观层次出发对该类问题进行数值模拟成为可能。建立反映混凝土细观组成的数值模型，能较直观地分析侵彻过程中弹体受力特点及侵彻规律，对改进弹体的侵彻效应及提高结构的防护能力有重要意义。

本文中，采用骨料随机投放思想，建立混凝土三维细观几何模型，并参考侵彻实验对模型有效性进行验证。从混凝土细观组成分析刚性弹正侵彻过程中弹道偏转的原因及可能影响因素。然后以弹体偏转角度为指标，研究混凝土细观因素(骨料随机分布、骨料强度、砂浆强度等)，弹体直径/骨料最大粒径比，以及侵彻速度对弹体偏转角度的影响。最后给出混凝土细观模型和均匀模型分别用于弹体侵彻数值模拟的适用范围。

1 混凝土细观数值模型建立

Z.M.Wang等[11]提出混凝土随机骨料模型，将混凝土视作由骨料、水泥砂浆以及两者之间的粘结带组成的三相非均质复合材料，采用骨料随机投放思路，实现混凝土的细观数值建模。本文在该模型的基础上，基于混凝土级配理论，建立细观混凝土模型，具体步骤如图1所示。

1.1 随机数产生

图1 细观模型建立流程图Fig.1 Flow diagram of meso-scopic modeling

模型中骨料位置的随机分布，根据蒙特卡罗法在计算机中生成的伪随机数来确定。采用VC++6.0在区间[0,1]上产生均匀分布的伪随机数X，然后给定区间上均匀分布的随机数序列，作为后续骨料投放的坐标基点。

1.2 骨料级配及投放区域的确定

工程材料或结构中，混凝土骨料的粒径分布区间广泛，且骨料粒径差别对于侵彻弹体受力影响较大，因此细观模型中应考虑混凝土的级配组成。根据混凝土所含骨料粒径范围，通常可分为一、二、三、四级配混凝土。参考W.B.Fuller等提出的三维级配曲线[12]，可以得到常用的几种级配骨料分布，如表1所示，Vs∶Vm∶Vb∶Vh为混凝土中小、中、大、巨大骨料的体积分数之比。

表1 不同级配骨料粒径分布

根据表1计算出不同尺寸试件中各种粒径的骨料颗粒数(其中粒径小于5 mm的骨料颗粒计入砂浆中)，然后根据骨料的投放区域生成几何模型。模型投放区域通过空间直角坐标系及柱坐标系实现，如：生成立方体试件，则采用空间立方体投放区域；生成圆柱体试件，则采用空间圆柱体投放区域。

1.3 骨料生成算法

根据实际碎石混凝土中骨料的特点，采用随机凸多面体模拟骨料的三维几何形状。此处的随机凸多面体以八面体骨料基为基础生长而成，并结合文献[13]，采用空间体积为标度对新生成顶点的位置进行控制，实现骨料形状为凸型骨料。

1.4 骨料投放算法

三维随机骨料在投放过程中为保证投放域内的骨料不会发生相互侵入的现象，采用点侵入凸多面体空间的判断、凸多面体空间侵入的特殊情况[13]对生成的多面体进行判断。根据上述随机多面体骨料的生成及投放算法，利用VC++6.0软件编制了三维随机凸面体骨料模型的程序3D-RAM。利用该程序生成的全集配混凝土骨料含量如图2所示。

图2 骨料投放示意图Fig.2 Schematic diagram of aggregate distribution

1.5 网格划分

有限元网格剖分是混凝土三维细观模型建立的难点。本文中采用背景网格划分法[14]进行混凝土各相介质的网格划分。具体步骤如下：基于背景网格，对骨料、砂浆及界面进行投影，图3(a)中网格分为骨料、砂浆、界面共3类。考虑骨料、砂浆及界面三相材料，如果某个单元的8个节点均落入骨料的投影范围内，则该单元类型为骨料单元。若单元的8个节点均落入砂浆区域内，则该单元的类型为砂浆单元。若单元的8个节点既有落入骨料范围又有落入砂浆范围的，则该单元为界面单元。三者之间采用共节点方式处理，此时界面单元的厚度为1个单元厚度(本文中单元最小尺寸为2 mm)。最终得到混凝土细观模型各组成部分如图3(b)～(d)所示。

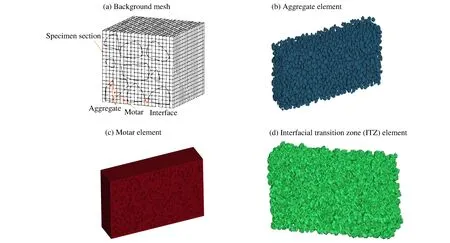
图3 细观模型各组成部分有限元剖分Fig.3 Each component’s FEM of meso-scopic model

2 数值模型有效性验证

通过弹/靶侵彻实验与数值模拟的对比，对以上建立的混凝土细观数值模型用于分析冲击问题的有效性进行验证，计算通过LS-DYNA有限元软件实现。

2.1 混凝土靶侵彻实验模拟

选取S.J.Hanchak等[15]的实验为验证分析对象，计算中弹体形状及靶板尺寸与文献中保持一致，实验中弹体未直接作用在钢筋上，因此数值模型中不考虑钢筋的作用。

混凝土单轴抗压强度为48 MPa，采用细观模型，最大骨料粒径为9.5 mm。对弹体采用MAT_RIGID模型；对骨料、砂浆及界面均采用K&C模型。计算中采用侵蚀判断准则作为单元的失效准则。相关模型参数见表2,表2中ρ为密度，E为弹性模量，μc为泊松比，σt为拉伸强度，σc为压缩强度。

表2 弹体及混凝土材料参数

表3给出了不同冲击速度v0下，数值模拟和实验得到的弹体剩余速度vr。从表3可以看出，数值计算的弹体剩余速度与实验值的相对误差在10%以内，且靶板宏观破坏模式与实验现象也较一致，如图4所示。这表明本文中所建立的混凝土细观模型可有效用于弹体侵彻模拟问题。

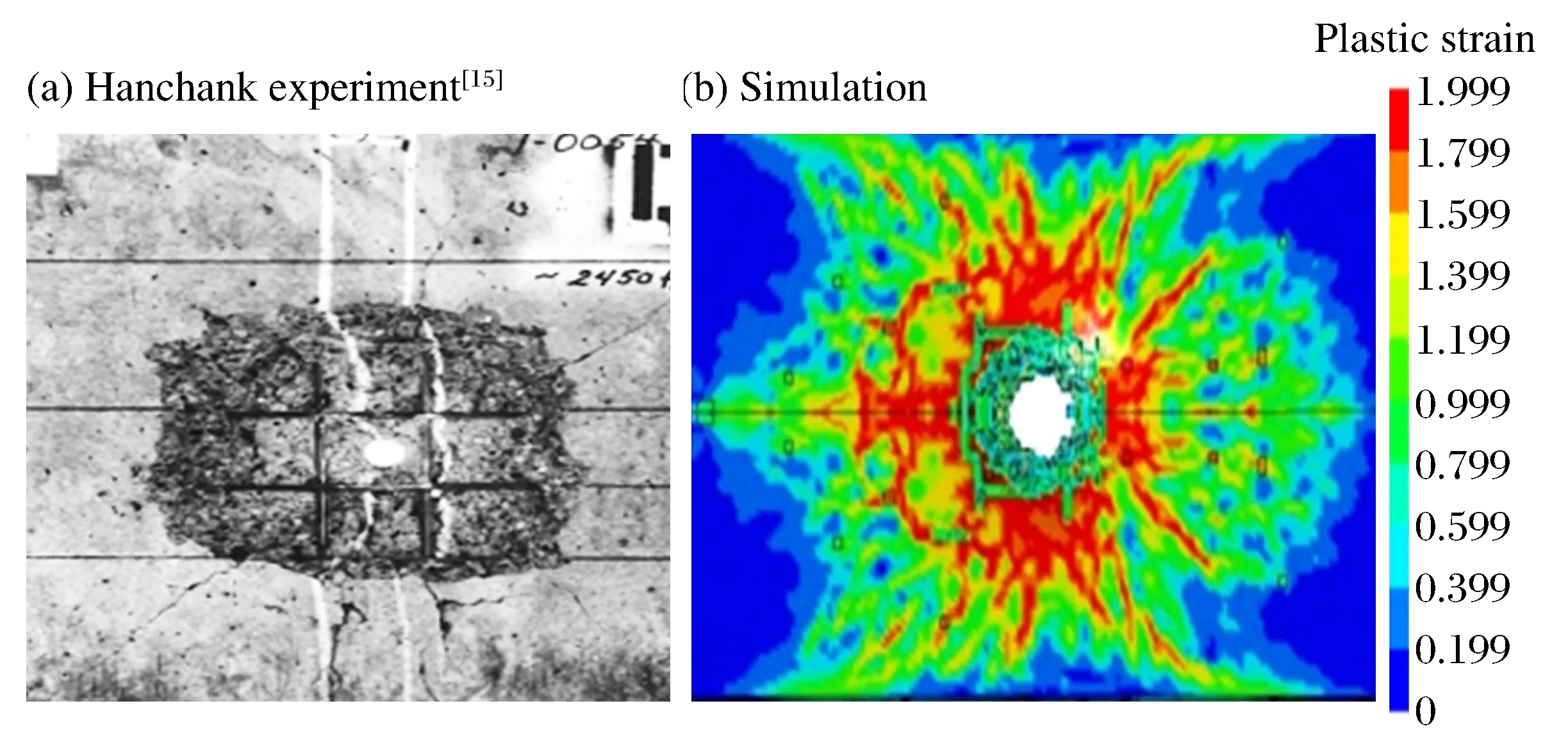
图4 靶板迎弹面破坏模式Fig.4 Failure mode of the target on the impact side

v0/(m·s-1)vr/(m·s-1)实验模拟36067733811361574342142376064494707496156331058947963

图5 弹体尺寸Fig.5 Projectile geometry

图6 混凝土靶板尺寸Fig.6 Concrete target geometry

2.2 数值模拟靶板尺寸

弹体侵彻混凝土靶板时存在边界效应。在弹速不超过800 m/s时，靶径与弹径之比约为30即可忽略侧面边界对侵彻过程的影响[16]。若对混凝土按均匀介质建模，该条件对于计算规模影响不大。但若基于细观模型，满足该条件则会导致计算量显著增加，效率很低。本文重点在于讨论弹体侵彻混凝土靶过程中的弹道偏转规律，为提高计算效率，此处对比2种靶体尺寸的计算结果，分析采用较小尺寸的靶板是否满足计算要求。

选择S.J.Hanchak等[15]实验中的弹体尺寸，见图5，其直径为25.4 mm。靶体尺寸布置如图6所示，W、H、T分别为宽、高、厚。模型1的靶板尺寸为800 mm×600 mm×400 mm，靶径与弹径之比满足大于30的要求；模型2的靶板在侵彻深度(H)方向保持高度不变，其余尺寸减小为模型1的一半，选为400 mm×600 mm×200 mm。模型参数与表2中一致。为了观察弹体侵彻的弹道偏转姿态，并减小计算规模，计算中采用1/2对称模型，约束弹靶在垂直于对称面方向上的位移及转动自由度，其余边界按无反射边界处理。也即人工假定：若有弹道偏转，仅发生在1/2对称模型的对称面上。

图7给出了2种靶体尺寸有限元计算结果。从图7可知，模型1和2得到的弹道轨迹偏转现象较一致，而模型2的计算量更小，因此后续分析中将采用400 mm×600 mm×200mm的靶板尺寸。

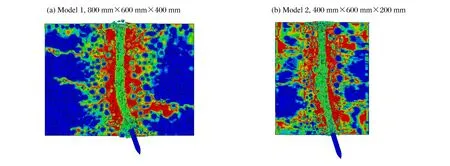
图7 不同尺寸的有限元模型弹道图Fig.7 Ballistc trajectories of finite element models with different dimensions

3 刚性弹正侵彻偏转影响因素分析

真实的弹体侵彻实验，即使是在严格的正侵彻条件下，都可能存在弹道偏转现象[10]。这里首先分别采用混凝土的均匀模型和细观模型进行数值模拟，对比刚性弹正侵彻混凝土靶的侵彻过程。然后从混凝土细观组成的角度分析弹道偏转的影响因素。

3.1 计算模型

数值计算中，混凝土靶板尺寸均为400 mm×600 mm×200 mm(见图6)，单元的基本尺寸为2 mm。弹体尺寸和形状如图5所示。细观模型中骨料的体积分数为40%，骨料级配为二级配，也即小石(5～20 mm)与中石(20～40 mm)的体积比为5.5∶4.5。显然，骨料尺寸与弹径相当甚至大于弹径，若骨料强度足够大，则可以设想对弹体侵彻有重要作用。弹体入射位置为靶板中点，入射速度为800 m/s，根据文献[17]可知，此时混凝土靶板侵彻过程中，可将弹体看作刚性弹。对弹体采用MAT_RIGID模型，对均匀模型中混凝土或细观模型中骨料、砂浆及界面均采用K&C模型，参数见表2，边界条件与2.2节中一致。

3.2 结果分析

3.2.1 现象分析

图8～9分别给出了混凝土为均匀介质模型和细观模型时，刚性弹以800 m/s的速度正侵彻靶板不同时刻的物理图像，其中骨料和砂浆抗压强度分别为160、15 MPa。从图8～9可以看出，在800 m/s的入射速度下：均匀模型中弹体基本没有发生偏转，保持正侵彻状态，此处由于显式动力计算过程中轻微扰动导致混凝土中的应变非严格对称；细观模型中，由于骨料分布的随机性，弹体在不同时刻出现不同程度的偏转现象。以上现象表明，骨料、砂浆的力学特性的差异及随机分布等因素对刚性弹体产生了不平衡力作用，导致侵彻方向变化，从正侵彻发展为斜侵彻。

图8 均匀模型混凝土靶的侵彻过程Fig.8 Penetration process of uniform concrete models

图9 细观建模的混凝土靶的侵彻过程Fig.9 Penetration process of mesoscopic concrete models

3.2.2 细观模型中弹体运动过程分析

由刚体运动学可知，刚性弹体的运动可以视作弹体质心的平动和绕质心的转动，如图10所示。弹体的偏转角度定义为弹体绕质心的转动角度，则弹体侵彻过程中的位移及姿态可以用质心坐标(xC,yC)和绕质心的偏转角度φ完全确定。选取对称面中轴线上A、B两个节点，两者x方向坐标值之差为Δx，偏转角度可以表示为φ=arcsin(Δx/L),L为弹体长度，如图11所示。

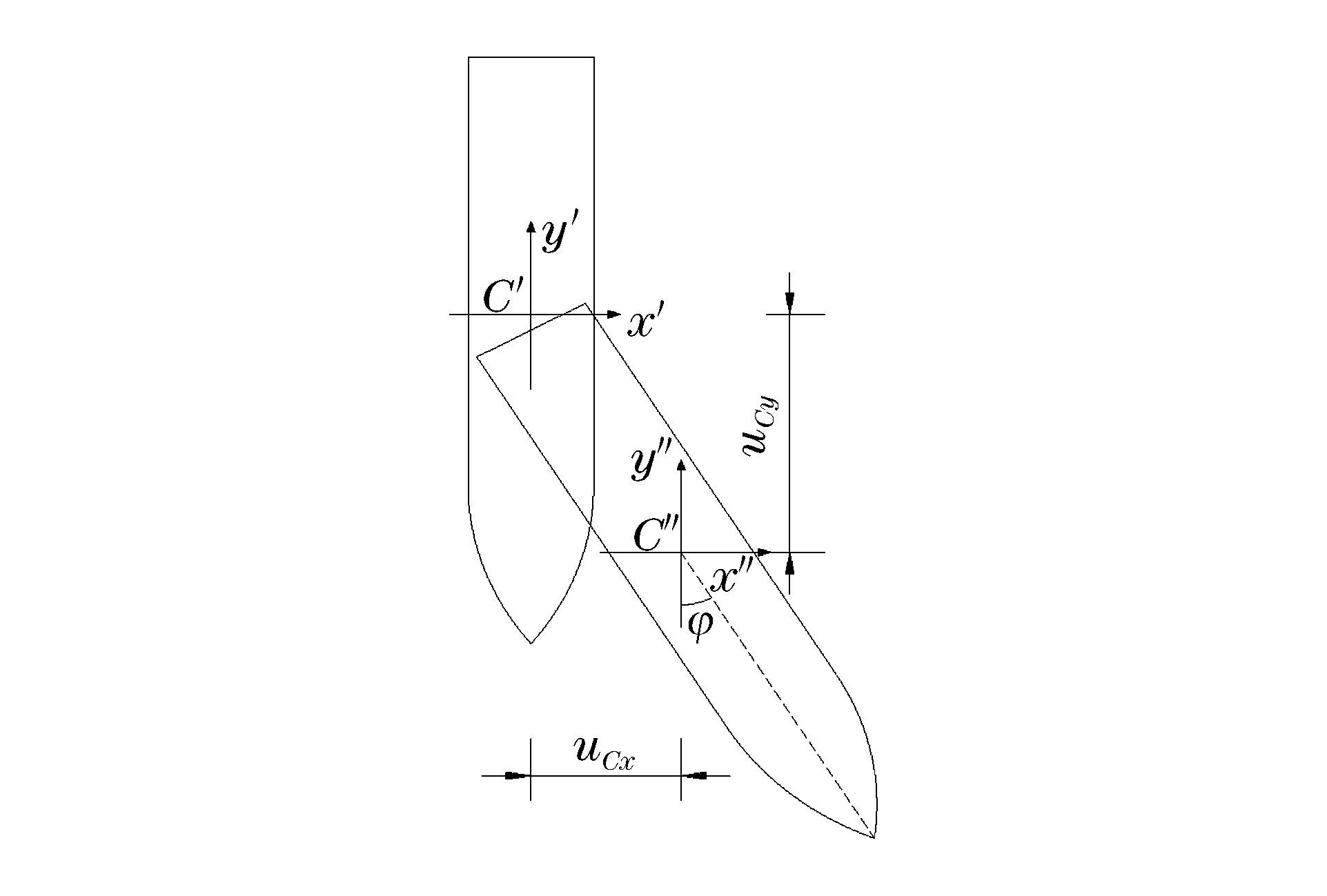
图10 侵彻过程中刚性弹运动示意图Fig.10 Motion of a rigid projectile during penetration

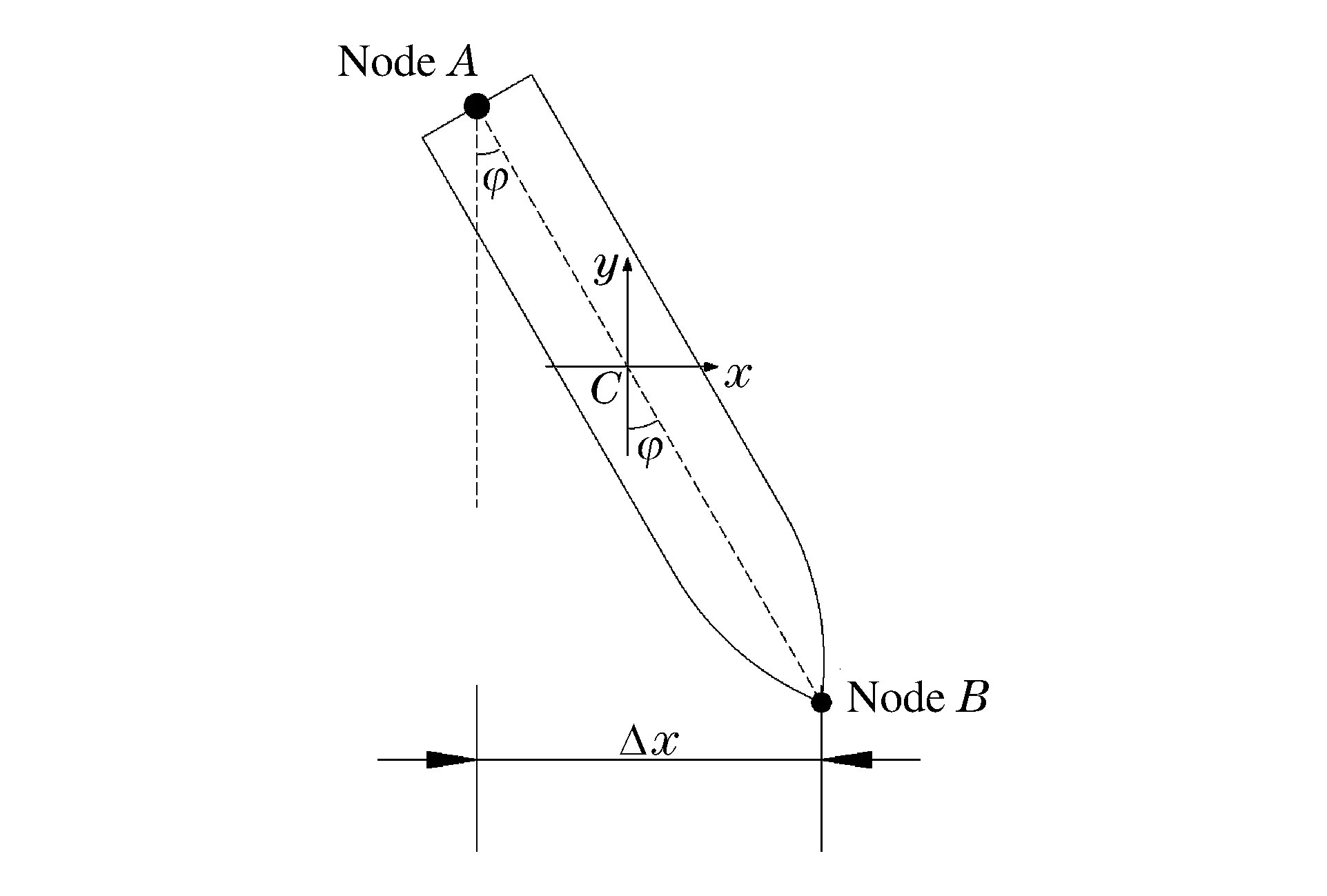
图11 弹体偏转角的定义Fig.11 Definition of the deflexion angle of a rigid projectile

为更清楚分析弹体在侵彻过程中的运动状态，图12给出了弹体质心水平加速度(aCx)、水平位移(uCx)及弹体偏转角度(φ)随时间的变化曲线,图中正值表示方向为水平向左，负号表示方向为水平向右。由图12(a)及图9，可以看出，弹体侵彻过程大致可分为以下几个时间段。

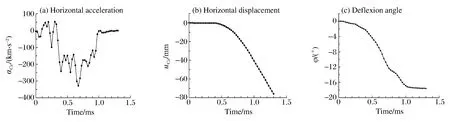
图12 弹体侵彻过程中各参数随时间的变化曲线Fig.12 Motion parameter-time curves of the projectile during penetration

(1)0～0.35 ms时间段内，弹体的水平加速度aCx在[-100，50] km/s2之间波动,如图12(a)所示，混凝土靶体对弹体在垂直于侵彻方向上产生交替变换的横向作用力；结合图9，该时间段，靶体内骨料分布较均匀，弹体所受到的横向加速度基本可以平衡，不足以使弹体质心产生横向位移(图12(b))，弹体的姿态几乎不发生变化(图12(c))；

(2)在0.35～0.40 ms时间段,从0.35 ms开始，弹体头部左侧连续碰撞到较大粒径的骨料(图9)，弹体向右侧的加速度随之增大(图12(a))，导致弹体开始出现向右的横向位移(图12(b))，并产生偏转现象(图12(c))；

(3)在0.40～1.00 ms时间段，弹体在侵彻过程中，在惯性作用下，由于骨料等的连续碰撞，弹体所受横向作用力保持稳定，弹体横向位移和偏转角度持续增加(图12(b)～(c))；

(4)1.00 ms以后，弹体到达靶板背面并穿透靶板，不再承受横向作用力，但弹体保持惯性仍有横向位移，其偏转角度保持恒定，直至出靶。最终弹体x方向位移为72.98 mm，偏转角度为17.53°。弹体侵彻姿态发生较大的变化，从正侵彻转变为带攻角的斜侵彻。

陈小伟等[18]研究发现，无论刚性弹正/斜侵彻混凝土靶，若按均匀介质考虑，弹体进入隧道区后将始终保持正侵彻姿态；仅对于斜侵彻的开坑阶段，由于不对称的侧向力作用，使得弹体承受绕质心的力矩作用，导致其运动姿态变化发生偏转。而与此不同的是，考虑混凝土细观建模后，即使刚性弹体正侵彻混凝土靶，在进入隧道区后，由于混凝土中多相材料性质的差异，导致弹体承受不对称力作用，其运动姿态仍可能变化并发生偏转(图9)。

3.2.3 偏转影响因素分析

通过上述侵彻过程的分析可知：刚性弹正侵彻混凝土靶过程中，弹体姿态的变化主要是由于混凝土中各相材料力学性能的差异引起弹体受到不对称作用力而导致的。其中，骨料作为混凝土的骨架，其粒径大小、位置分布等都对侵彻过程中弹体受力状态存在较大影响。另一方面，侵彻过程中弹头所受阻力可用空腔膨胀理论[19]进行分析，一般认为弹头表面法向力不仅决定于靶材性质和侵彻速度，还受弹头形状影响，该阻力的横向分量将导致弹体弹道偏转。从弹体结构出发，弹体偏转角度还与弹体长径比相关。因此，基于混凝土细观建模的弹体正侵彻混凝土细观靶过程中，影响弹体偏转的因素主要有混凝土各相材料(骨料、砂浆及界面等)力学性能(如强度、硬度、断裂能等)、骨料几何及位置分布、弹体初始撞击速度、弹体头部形状和弹体长径比等。

4 弹体弹道偏转规律分析

针对前述影响弹体弹道偏转的因素分析，本节中通过改变部分参数值进行数值模拟，分析这些参数对弹体弹道偏转的影响规律。混凝土靶板尺寸、骨料级配及含量、弹体尺寸等均与3.1节中保持一致，弹体初始侵彻速度为800 m/s。仍采用1/2对称模型和边界约束。对混凝土中砂浆和骨料均采用K&C模型，对弹材取刚性模型，相关基本参数见表2。不同工况计算中，根据需要改变个别参数值。在考虑骨料随机性影响时，则按同一靶体不同入射位置进行分析，即以模型对称面中点为基点，按间距50 mm共取5个点为弹体入射位置，依次命名为L1、L2、C、R1及R2，如图13所示。

4.1 骨料位置随机分布对正侵彻弹体偏转角度的影响

图14给出了弹体在不同入射位置(可认为骨料分布随机不同)正侵彻混凝土靶过程中偏转角度的时程曲线。显然，入射位置不同，弹体偏转角度变化完全迥异。其一表现在最大偏转角度值不同：当弹体从中点C位置侵入，最大偏转角为11.70°；而弹体从L1位置侵入，最大偏转角仅为1.10°，两者相差约10倍。其二表现在偏转角的正负(即左右)方向不同：弹体从不同位置侵入时，其偏转角在左右方向上呈现一定波动，且偏转方向可不同，如从位置L2侵入时，弹体向左边偏转，从位置R1侵入时，弹体向右偏转。因此，可认为混凝土靶中骨料的随机分布对弹体偏转角度影响甚大。分析发现：由于靶体内骨料分布的随机性导致弹体受力发生较大变化。在混凝土侵彻的数值模拟中，若采用均匀介质模型，有可能不足以全面反映弹靶侵彻/穿甲的真实物理过程。

图13 靶体尺寸及侵彻位置示意图Fig.13 Target dimension and penetration location

图14 骨料随机分布对弹体偏转的影响 Fig.14 Projectile deflection affected by aggregate random distribution

4.2 骨料和砂浆的强度对正侵彻弹体偏转角度的影响

图15～16分别给出了弹体在骨料和砂浆不同强度的条件下正侵彻混凝土靶过程中偏转角度的时程曲线。这里及以下仅给出在靶板中点C位置入射的结果分析，可认为从其余位置入射相应的参数影响规律一致。从图15～16可以看出，不同骨料或砂浆强度下，同一位置侵入弹体的偏转方向的变化规律基本一致。但弹体的最大偏转角随着骨料强度的增大而增大，特别地，当骨料强度从120 MPa增加到160 MPa时，偏转角度最大值从1.89°增大到11.70°。这是由于骨料强度增大，加剧了其各相介质力学性能的差异，非均匀性表现更明显，弹体受到骨料的非对称力作用突然增大，导致偏转角增大。显著不同的是，如图16所示，随着砂浆强度的增大，弹体的偏转角变小，当砂浆强度达到20 MPa时，可基本认为弹体无偏转，这时砂浆与骨料的强度差减异小，混凝土材料趋于均匀。

一般地，砂浆强度小于骨料强度，当骨料强度增大时，骨料与砂浆强度的差异将显著增大，这将增大混凝土不同相材料性能的差异并导致其随机性增强。而骨料强度一定，仅增大砂浆强度，则使骨料与砂浆强度的差异减小，相反导致混凝土不同相材料的性能更均匀。对比可知：当骨料强度从60 MPa提高至160 MPa时，弹体偏转角最大值从1.12°变为11.70°，增大约10.4倍；而砂浆强度从30 MPa降至5 MPa时，弹体偏转角最大值从1.31°变为18.50°，增大约14倍。这说明砂浆强度的变化对弹体偏转的影响较骨料强度的的变化对其的影响显著。

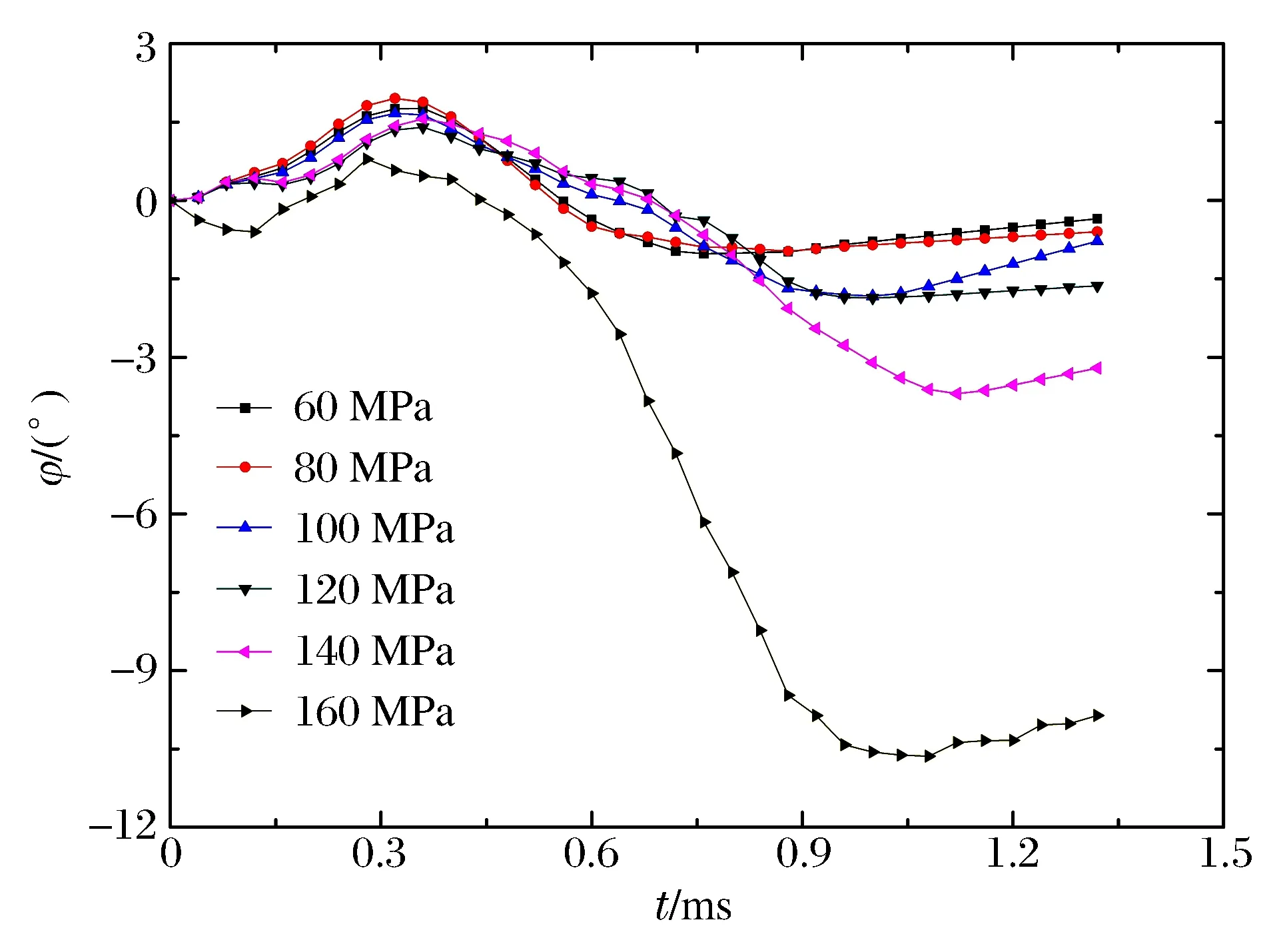
图15 骨料强度对弹体偏转的影响Fig.15 Projectile deflection affected by aggregate strength

图16 砂浆强度对弹体偏转的影响Fig.16 Projectile deflection affected by motar strength

4.3 弹径/骨料粒径比和侵彻速度对正侵彻弹体偏转角度的影响

为便于无量纲分析，在弹体其他条件一定情况下，定义弹径/骨料粒径比为γ=D/d，其中D为子弹直径，d为骨料最大粒径。计算中仍然采用图5所示的弹形。为排除骨料随机分布影响，这里仅通过改变弹体尺寸来实现不同的γ值，γ分别取0.40、0.85、1.67和2.67，则对应的最大骨料尺寸分别为65、30、15及10 mm。侵彻速度范围为300～800 m/s，计算模型及相关的简化原则均与3.1节中保持一致。图17为不同入射速度下，不同γ值时，弹体偏转角度的时程曲线,从图17可以得出以下规律：

(1)同一侵彻速度下，弹体偏转角度随γ增大而逐渐减小；当γ增大到1.67时，偏转角小于1.00°，可认为无偏转。这是由于γ越大，则骨料越小，其他条件一致时，可认为混凝土各相材料趋于均匀。因此，在骨料强度一定时，当弹径/骨料粒径比达到一定值，可以不考虑混凝土细观组成的影响，仅采用连续均匀介质进行模拟即可。

(2)同一γ值，当γ<1.67时，随着侵彻速度增加，弹体偏转角度有较大增长。其中γ=0.40，初始侵彻速度为800 m/s时偏转角已经达到15.30°。当γ>1.67时，随着初始侵彻速度的增大，偏转角基本无变化，这与第1点相同。因此，将骨料的强度变化考虑进来，保守可认为在本文的计算条件下，若γ>2.00，即骨料最大尺寸为弹径的1/2时，刚性弹正侵彻混凝土靶时不发生弹道偏转，可将混凝土视作均匀介质。相反，若γ<2.00，弹道偏转不可忽略，混凝土各相材料对侵彻影响较大，必须采用细观模型才能正确描述弹体侵彻过程。

(3)弹体姿态在初始阶段改变甚小，这与弹体正侵彻的实验观察相吻合。初始侵彻速度较小，弹体正侵彻过程中偏转角幅值波动较大，这表明低速侵彻弹体的运动姿态容易受非对称力作用而改变。当撞击速度增高时，弹体偏转角幅值在侵彻过程中单调增加，这是由于弹体具有更大运动惯性使然。

图17 不同入射速度下，不同γ值时，弹体偏转角度的时程曲线Fig.17 Deflection angle-time curves of the projectiles at different γ values and different impact velocities

5 结 论

基于混凝土骨料随机投放的思想，建立了混凝土细观数值模型，并进行了有效性验证。以弹/靶正侵彻实验为基础，分析了刚性弹侵彻混凝土细观模型的侵彻过程，探讨了混凝土细观参数对弹体偏转的影响。得到如下结论：

(1)与均匀模型模拟不同的是，用混凝土细观模型模拟刚性弹正侵彻时，在侵彻隧道区可能发生弹体弹道偏转。也即，混凝土细观数值模型可以较好反映弹体正侵彻过程中弹道偏转等典型物理现象。

(2)混凝土细观参数对于弹体弹道偏转有显著影响。随着骨料强度的降低及砂浆强度的增大，弹体偏转角度有所降低，且砂浆强度变化对于弹道偏转影响较骨料强度变化大。

(3)考虑刚性弹正侵彻的弹道偏转时，存在一个弹体直径/骨料最大粒径比的特征比值。也即，当弹径足够大时，混凝土细观组成对于弹道偏转影响可以忽略，可将混凝土当作均匀介质处理；反之，骨料足够大，则应采用细观模型进行数值模拟。

[1] Backmann M E, Goldsmith W. The mechanics of penetration of projectiles into targets[J]. International Journal of Engineering Science, 1978,16(1):1-99.

[2] 钱伟长.穿甲力学[M].北京:国防工业出版社,1984:23-35.

[3] Goldsmith W. Review: Non-ideal projectile impact on targets[J]. International Journal of Impact Engineering, 1999,22(2/3):95-395.

[4] Corbett G G, Reid S R, Johnson W. Impact loading of plates and shells by free-flying projectiles: A review[J]. International Journal of Impact Engineering, 1996,18(2):141-230.

[5] Li Q M, Reid S R, Wen H M, et al. Local impact effects of hard missiles on concrete targets[J]. International Journal of Impact Engineering, 2006,32(1/2/3/4):224-284.

[6] Warren T L, Fossum A F, Frew D J. Penetration into low-strength (23 MPa) concrete: Target characterization and simulations[J]. International Journal of Impact Engineering, 2004,30(5):477-503.

[7] Forrestal M J, Frew D J, Hickerson J P, et al. Penetration of concrete targets with deceleration-time measurements[J]. International Journal of Impact Engineering, 2003,28(5):479-497.

[8] 陈小伟.穿甲/侵彻问题的若干工程研究进展[J].力学进展,2009,39(3):316-351. Chen Xiaowei. Advances in the penetration/perforation of rigid projectiles[J]. Advances in Mechanics, 2009,39(3):316-351.

[9] Neville A M. Properties of concrete[M]. 5ed. Prentice Hall, 2012:112-119.

[10] 何翔,徐翔云,孙桂娟,等.弹体高速侵彻混凝土的效应实验[J].爆炸与冲击,2010,30(1):1-6. He Xiang, Xu Xiangyun, Sun Guijuan, et al. Experimental investigation on projectiles’ high-velocity penetration into concrete target[J]. Explosion and Shock Waves, 2010,30(1):1-6.

[11] Wang Z M, Kwan A K H, Chan H C. Mesoscopic study of concrete I: Generation of random aggregate structure and finite element mesh[J]. Computers and Structures, 1999,70(5):533-544.

[12] Fuller W B, Thompson S E. The laws of proportioning concrete[M]∥The American Society of Civil Engineers. Transactions of the American Society of Civil Engineers: Vol.LIX, 1926:67-172.

[13] 刘光廷,高政国.三维凸型混凝土骨料随机投放算法[J].清华大学学报(自然科学版),2003,43(8):1120-1123. Liu Guangting, Gao Zhengguo.Random 3-D aggregate structure for concrete[J]. Journal of Tsinghua University (Science and Technology), 2003,43(8):1120-1123.

[14] Vervuurt A. Interface fracture in concrete[D]. Delft University of Technology, 1997:45-49.

[15] Hanchak S J, Forrestal M J. Perforation of concrete slabs with 48 MPa (7 ksi) and 140 MPa (20 ksi) unconfined compressive strengths[J]. International Journal of Impact Engineering, 1992,12(1):1-7.

[16] 梁斌.弹丸对有界混凝土靶侵彻研究[D].绵阳:中国工程物理研究院,2004:62-89.

[17] 陈小伟,李继承.刚性弹侵彻深度和阻力的比较分析[J].爆炸与冲击,2009,29(6):584-589. Chen Xiaowei, Li Jicheng. Analysis on the penetration depth and resistive force in the deep penetration of a rigid projectile[J]. Explosion and Shock Waves, 2009,29(6):584-589.

[18] Chen Xiaowei. Dynamics of metallic and reinforced concrete targets subjected to projectile impact[D]. Singapore: Nanyang Technological University, 2003:50-67.

[19] 李志康,黄风雷.混凝土材料的动态空腔膨胀理论[J].爆炸与冲击,2009,29(1):95-100. Li Zhikang, Huang Fenglei. dynamic spherical cavity-expansion theory for concrete materials[J]. Explosion and Shock Waves, 2009,29(6):95-100.

(责任编辑 张凌云)

On ballistic trajectory of rigid projectile normal penetration based on a meso-scopic concrete model

Deng Yongjun1,2, Chen Xiaowei1,2, Yao Yong1, Yang Tao1

(1.SchoolofCivilEngineeringandArchitecture,SouthwestUniversityofScienceandTechnology,Mianyang621000,Sichuan,China;2.InstituteofSystemsEngineering,ChinaAcademyofEngineeringPhysics,Mianyang621999,Sichuan,China)

To study the effect of the concrete’s mesoscopic factors on the deflection of the rigid projectile’s ballistic trajectory, we established a 3-D mesoscopic model for the concrete based on the idea of randomly distributed aggregates, analyzed the causes and possible contributing factors of the ballistic trajectory deflection of the rigid projectile penetrating into a concrete target, and examined quantitatively the influence of the mesoscopic factors of the concrete. The results show that the mesoscopic concrete model is able to reflect the typical physical phenomena of a projectile’s normal penetration, that the mesoscopic factors have significant effect on the deflection of the ballistic trajectory as the rigid projectile is penetrating into the mesoscopic concrete, and that there exists a characteristic ratio of the projectile’s diameter to the largest possible diameter of the aggregate.

concrete; meso-scopic model; rigid projectile; normal penetration; ballistic trajectory deflexion

10.11883/1001-1455(2017)03-0377-10

2015-10-09；

2016-03-27

国家自然科学基金项目(11225213,11390361,11390362);中国工程物理研究院重点学科项目

邓勇军(1987— ),男,博士研究生,助理研究员; 通信作者: 陈小伟,chenxiaoweintu@yahoo.com。

O382 国标学科代码： 13035

A