基于Mogi-Coulomb准则的圆形巷道围岩塑性区分析

2021-02-25欧阳蕊灿王卫军

矿业工程研究 2021年4期

欧阳蕊灿,王卫军

(湖南科技大学资源环境与安全工程学院,湖南湘潭 411201)

巷道围岩的稳定性与其塑性区有着本质的关联,塑性区的大小和形态决定着巷道的稳定性,因此研究塑性区的范围对围岩支护设计有重要意义.国内外学者关于塑性区的研究已有了丰富的成果.张小波等[1]以弹塑性力学为理论,在考虑中间主应力的基础上对巷道围岩塑性区展开了研究;王卫军等[2]在M-C强度准则的基础上,推导了非等压条件下圆形巷道塑性区边界方程;郭晓菲等[3]通过塑性区边界方程得到了塑性区的形态变化规律;袁超等[4]研究了岩石力学特性等对塑性区范围和形态的影响;陈立伟等[5]通过岩石的统一强度理论得到了可以描述塑性区边界形态的方程;张常光等[6-7]推导了理想弹塑性体塑性区围岩应力与位移的新解;马念杰等[8]通过研究围岩偏应力的分布规律得出了偏应力作用下的塑性区半径表达式;李宇翔等[9]研究了在非均匀应力场下中间主应力对塑性区的影响并得到了塑性区边界方程的近似隐式解;骆开静等[10]在考虑蠕变下建立了软化模型,并根据此软化模型对塑性区展开了研究;陈梁等[11]基于D-P强度准则,结合考虑岩石流变等对巷道围岩塑性区与破裂区进行了分析讨论;董海龙等[12]在考虑峰后软化的条件下推导了塑性区边界方程,并结合总荷载不变理论提供了塑性区半径的近似解.这些研究成果对塑性区的研究有着重要的意义.本文基于Mogi-Coulomb强度准则研究岩石岩性与中间主应力对巷道围岩塑性区形态与大小的作用，研究结果对巷道围岩支护设计具有重要意义.

1 Mogi-Coulomb准则

目前大多数学者一般采用Mohr-Coulomb强度准则研究地下工程问题,实际上,地下工程岩体处于三维应力状态,而Mogi-Coulomb准则[13-16]是基于大量的真三轴实验所得,采用Mogi-Coulomb准则研究地下工程问题更加符合实际情况.Mogi-Coulomb准则在σ2=σ3(σ2为中间主应力,σ3为最小主应力)时则退化成Mohr-Coulomb强度准则.Mogi-Coulomb准则表示为

τoct=a+bσm,2;

(1)

(2)

(3)

式中:τoct为八面体剪应力；a,b为材料参数;σm,2为作用在剪切面上平均有效正应力.通过式(2)可知,Mogi-Coulomb准则考虑了中间应力σ2的作用.Mogi-Coulomb准则的外形函数与Mohr-Coulomb强度准则密切相关,其外形函数可由图1表示.

图1 Mogi-Coulomb准则的外形函数

当σ2=σ3时,由Mohr-Coulomb强度准则可以得到:

(4)

式中:φ为岩石的内摩擦角;c为岩石的内聚力.

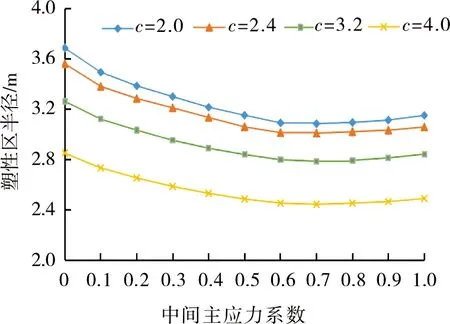
为了更好地研究中间主应力的影响,设定中间主应力系数的表达式为式(5),且0≤d≤1,当d=0时,为轴对称的三轴压缩状态;当d=1时,为轴对称三轴拉伸状态;当0

(5)

由式(5)变形可得σ2=dσ1+(1-d)σ3,将表达式代入式(1)整理后得到Mogi-Coulomb准则如下:

σ1=Aσ3+B.

(6)

(7)

式中:T1=2[2(d2-d+1)]1/2,当中间主应力系数d=0或1时,则没有考虑中间主应力的影响.

2 圆形巷道围岩塑性区边界方程计算

2.1 力学模型

巷道围岩结构复杂,为了便于理论分析,对巷道围岩提出以下基本假设:

1)围岩是满足Mogi-Coulomb准则的连续、均匀、各向同性的理想弹塑性材料.

2)巷道为深埋巷道且巷道截面为圆形,巷道半径为R0,巷道无限长,按平面应变问题处理.

3)巷道围岩处于两向非等压应力场,P0与kP0分别为作用在巷道围岩上的垂直与水平应力,k为侧压力系数,Rp表示塑性区半径,支护力Pi视为均匀分布,r为围岩中任一质点到巷道中心的距离.力学模型如图2所示.

图2 力学模型

2.2 塑性区边界方程求解

目前大多数研究采用近似隐式法来求巷道围岩塑性区的边界方程,采用近似隐式法求解的巷道围岩塑性区可以得到不同侧压系数下塑性区的形态,圆巷围岩塑性形态的变化规律可由其较好地反映出来.所以本文通过近似隐式法求圆形巷道围岩塑性区边界方程[17].

当前还没有精确的解析能分析非均匀应力条件下的圆形巷道围岩的弹塑性区.大多数国内与国外的学者均是通过假设巷道开挖后围岩仍然处于弹性应力状态这一条件，结合弹性理论的基础上研究圆形巷道处于非均匀应力场开挖后的围岩弹性应力,其表达式为

(8)

弹性力学中,求解主应力的表达式为

(9)

在实际工程中，巷道围岩受力问题可以作为平面问题处理,利用转化公式可得到用极坐标表示的各应力关系式为

(10)

围岩应力达到起塑条件后满足Mogi-Coulomb准则方程:

f=σ1-Aσ3-B.

(11)

将σ1,σ3代入式(11)后令f=0可得

(12)

通过化解后得到塑性区边界隐形方程为

(13)

式中:

m0=1/4[(T1+3b)/(T1-3b)+1]2(k-1)2P02-[(T1+3b)/(T1-3b)-1]2(k+1)2P02-[(T1+3b)/(T1-3b)-1][6a/(T1-3b)](k+1)P0-[6a/(T1-3b)]2；

m1=1/4[(T1+3b)/(T1-3b)+1]2[2(k-1)P0(2Pi-kP0-P0)cos 2θ-4(k-1)2P02(2cos22θ-1)]+[(T1+

3b)/(T1-3b)-1]2(k2-1)P02cos 2θ+2[(T1+3b)/(T1-3b)-1][6a/(T1-3b)](k-1)P0cos 2θ；

m2=1/4[(T1+3b)/(T1-3b)+1]2[(kP0+P0-2Pi)2+4(k-1)P0(kP0+P0-2Pi)cos 2θ+2(k-1)2P02(6cos22θ-1)]-[(T1+3b)/(T1-3b)-1]2(k-1)2P02cos22θ；

m3=3/2[(T1+3b)/(T1-3b)+1]2(k-1)P0[-(k+1)P0cos 2θ+2Picos 2θ-2(k-1)P0]；

m4=9/4[(T1+3b)/(T1-3b)+1]2(k-1)2P02.

式(13)即为基于Mogi-Coulomb准则下的近似隐式法所得的巷道围岩塑性区边界方程.将侧压力系数k=1代入式(13),即可得到均匀应力场下塑性区边界方程,当侧压力系数k≠1时可求出非均匀应力场下的塑性区半径表达式.

3 算列分析

3.1 内聚力对巷道围岩塑性区的影响

设定一定的圆形巷道围岩力学参数:取巷道半径R0=2 m,原岩地应力P0=18 MPa,支护力Pi=0.75 MPa,内摩擦角φ=25°,中间主应力系数d=0,将参数代入式(13)可以得到侧压系数k=1,k=0.7,k=0.3这3个不同条件下的内聚力对巷道围岩塑性区的影响如图3所示.由图3可知,在相同侧压力系数下,随着内聚力的增大,塑性区形态没有发生改变但巷道围岩塑性区的半径减小,且随着内聚力增大,塑性区半径减小的速度增大.此外,相同内聚力条件下,随着侧压系数k的增大,水平轴上的塑性区半径越来越大,竖轴上的塑性区半径越来越小.

图3 内聚力与巷道围岩塑性区的关系

3.2 内摩擦角对巷道围岩塑性区的影响

巷道半径R0=2 m,原岩地应力P0=18 MPa,支护力Pi=0.75 MPa,内聚力c=2 MPa,中间主应力系数d=0,将各力学参数代入式(13)可以得到侧压系数k=1,k=0.7,k=0.3这3个不同条件下的内摩擦角与巷道围岩塑性区的关系如图4所示.由图4可知,内摩擦角的变化不改变塑性区的形态但影响塑性区的大小,内摩擦角与塑性区的大小变化趋势相反,并且随着内摩擦角的增大,塑性区半径减小的速度减小.

图4 内摩擦角与巷道围岩塑性区的关系

3.3 中间主应力系数对巷道围岩塑性区的影响

巷道半径R0=2 m,原岩地应力P0=18 MPa,支护力Pi=0.75 MPa,内摩擦角φ=25°,侧压力系数k=1.将参数代入式(13)可得到中间主应力系数与塑性区半径的关系如图5所示.由图5可知,当0≤d≤0.7时,随着中间主应力系数的增加,塑性区的半径逐渐减小,当c=2时,塑性区半径由3.688减小至3.088，c=2.4时,塑性区半径由3.563减小至3.012，c=3.2时,塑性区半径由3.265减小至2.789，c=4时,塑性区半径由2.851减小至2.445；当0.7≤d≤1时,随着中间主应力系数的增加,塑性区的半径却呈现出增长趋势,当c=2时,塑性区半径由3.088减增加至3.153，c=2.4时,塑性区半径由3.012增加至3.061，c=3.2时,塑性区半径由2.789增加至2.845，c=4时,塑性区半径由2.445增大至2.493.说明中间主应力对巷道围岩塑性区半径的影响具有区间效应.因此，在一定范围内增大中间主应力系数对巷道围岩的变形与塑性区的扩展具有一定的抑制作用.