非平稳时序数据的分段辨识及其递推算法①

黄雄波

(佛山职业技术学院 电子信息系,佛山 528137)

非平稳时序数据的分段辨识及其递推算法①

黄雄波

(佛山职业技术学院 电子信息系,佛山 528137)

在实际生活中,广泛地存在着一类在整体上属于非平稳但又可转化为数段局部平稳的时序数据,对该类非平稳时序数据的辨识问题进行了研究,并提出了一种具有递推机制的分段辨识算法.该算法从平稳时序数据的定义出发,以均值、方差及自相关函数等数字统计特征为校验统计量,构造了具有递推机制的均值突变点、方差突变点及自相关函数突变点的析出算法,在此基础上,从被辨识的非平稳序列中划分出数段局部平稳的子序列,进一步,应用Burg算法对各局部平稳子序列进行了自回归的递推辨识.实验表明,新设计的算法能以较小的位置偏差析出各局部平稳子序列的分界点,同时,在保证较高精度的辨识条件下,计算效能获得了显著的提升.

非平稳时序数据;局部平稳;分段辨识;递推;分界点;自回归模型

1 引言

时序数据根据其统计结构是否具有时变的特点,可分为平稳序列和非平稳序列两大类,通常,人们所获取到的时序数据大多为非平稳序列,也就是说,其有关的统计特性是随着时间t的变化而变化的.对于平稳时序数据而言,其线性辨识模型主要有三种, AR(自回归)模型、MA(滑动平均)模型和自回归滑动平均(ARMA)模型,这些模型可以相互转换,而辨识的主要任务有两个方面,辨识模型阶次的确定和辨识模型参数的估计.近年来,众多专家学者围绕这三种辨识模型展开了系统而深入的研究[1-9],例如,张贤达针对带有高斯ARMA噪声的平稳时序数据,提出了一种高阶累量的MA模型辨识算法;熊渊博研究了一种线性算法,将ARMA模型辨识问题中的非线性求解问题化简为求解两组线性方程组;周毅等通过用AR模型等价ARMA模型的思想,提出了一种确定ARMA模型参数估计方法,并给出了计算等价 AR模型参数估计的依阶次递增递推算法.

相对地,非平稳时序数据还没有形成统一而完整的分析方法[10,11].据此,在实际应用中,通常是运用适当的数学变换把非平稳时序数据转化为平稳时序数据,并以此作为实际物理过程的近似.例如,经典的博克斯-詹金斯辨识方法就是通过对非平稳时序数据进行有限次的差分处理,把非平稳序列化为平稳序列;朱学锋等基于Mallat快速小波算法对非平稳时序数据进行了分解和重构,进而获得了趋势项序列和剔除趋势项后的零均值平稳时序数据[12];林树宽等针对时序数据的非平稳性,通过经验模式分解得到了若干个平稳序列和趋势项,在此基础上,对每个平稳序列建立相应的辨识模型[13].

在实际生活中,广泛地存在着一类在整体上属于非平稳但又可转化为数段局部平稳的时序数据, P.M.Djuric等最早应用贝叶斯法对该类辨识问题进行了研究,并导出了一个关于分段数、各段自回归模型阶数和各段之间分界点的优化方程[14];在此基础上,王文华等推导出一些具有递归关系的求解表达式,从而有效地简化了优化方程的求解[15];为进一步提升计算效能,陈颖等结合自回归AR(Auto regressive)模型本身固有的特性,提出了直接递推多维联合分布概率的优化方程求解方法[16].总体而言,基于贝叶斯法框架的辨识算法仍然存在着计算复杂的效率问题,究其原因是由于在估计最优划分参数值时需要计算多维条件的分布概率.据此,本文拟从平稳时序数据的定义出发,设计实现一种新的具有递推机制的分段辨识算法,该算法的主要思想是:以均值、方差及自相关函数等数字统计特征为校验统计量,构造具有递推机制的均值突变点、方差突变点及自相关函数突变点的析出算法,进而能快速有效地析出了各局部平稳子序列的分界点,最后基于自回归AR模型对这些局部平稳子序列进行递推辨识.实验结果表明,该辨识算法在保证辨识精度的基础上获得了显著的计算效能的提升.

2 问题描述

2.1 非平稳时序数据的数字统计特征描述

从定义1易知,若某一时序数据为非平稳时序数据,则它的均值、方差及自相关函数等数字统计特征将部分或全部地随时间t的变化而变化.据此,可用如下的时变函数对上述非平稳时序数据的统计特征进行描述:

均值为:

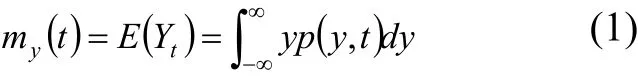
方差为:

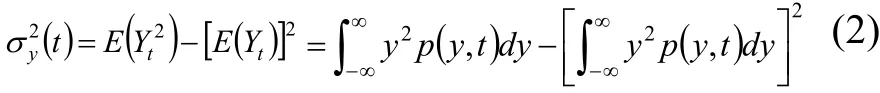
自相关函数为:

2.2 分段局部平稳时序数据的辨识问题

1)在0£t£n范围内具有非平稳的特征;

从定义2可知,分段局部平稳时序数据Yt的部分或全部统计特性在一些时刻(如定义中的e,f,…,g)里发生突变,但对各独立的子序列而言,它们又为平稳子序列.通常,也把这些突变时刻称为分界点.

在现实生活中,严格意义上的平稳序列是很难找到的,但很多真实序列在某一局部的时间范围内仍可用平稳序列来获得较为精确的描述,据此,研究分段局部平稳时序数据的辨识算法有着较为重要的现实意义.对分段局部平稳时序数据进行辨识,其首要的问题是找出各局部平稳子序列之间的分界点,其次是确定这些子序列的模型阶次和辨识参数.

3 非平稳时序数据的分段辨识算法

3.1 算法的设计原理

1)分界点的析出方法

对于某一平稳时序数据而言,将它拆分为m段样本长度为k的子序列(各段子序列的样本长度也可以不相等),则这些子序列的均值、方差和自相关函数的样本参数估计值可分别用如下的算式进行计算:

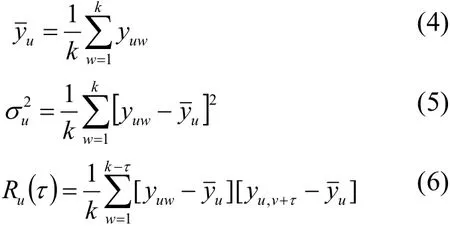
如前所述,这些从平稳序列拆分出来的子序列都应具有一致的数字统计特征,即任两个子序列之间的均值、方差和自相关函数等数字特征不应有显著性的差异.据此,以上述数字特征的理论方差为校验统计量,取显著水平α=0.05,若式(7)～(9)同时成立,则可判定u,v两个子序列是属于同一平稳序列[18-19].

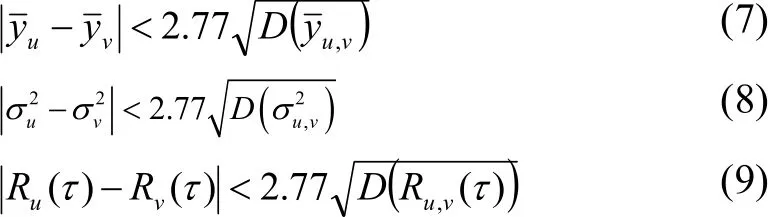
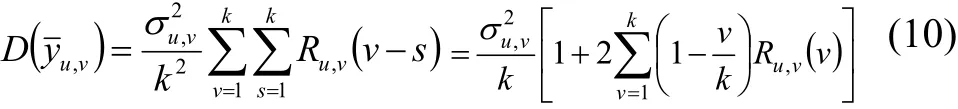
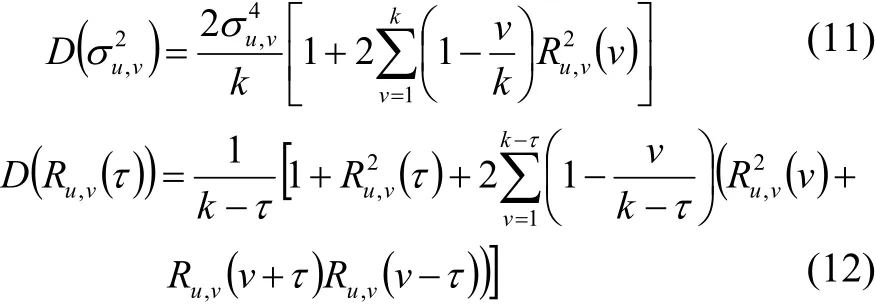
根据上述的分析,我们可以得到一种如下的局部平稳时序数据分界点的析出算法:按照自左到右的次序往原序列添加Step(Step≥1)个样本数据,并利用式(4)～(6)分别计算原序列的及添加数据后的新序列的同时,利用式(10)～(12)分别计算出然后根据式(7)～(9)对两个子序列的均值、方差和自相关函数等数字特征的显著性进行判别,从而决定当前所添加的第Step点是否为突变点.重复遍历处理整个序列,直至从原序列中析出所有的突变点为止.

从式(10)～(12)易知,对添加样本后的序列进行相关的显著性校验时,均需要显式调用均值、方差和自相关函数的样本参数估计值,为了更好地提高算法的计算效能,有必要对式(4)～(5)进行递推计算的改进.

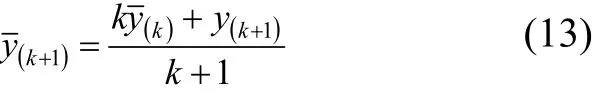
由于:

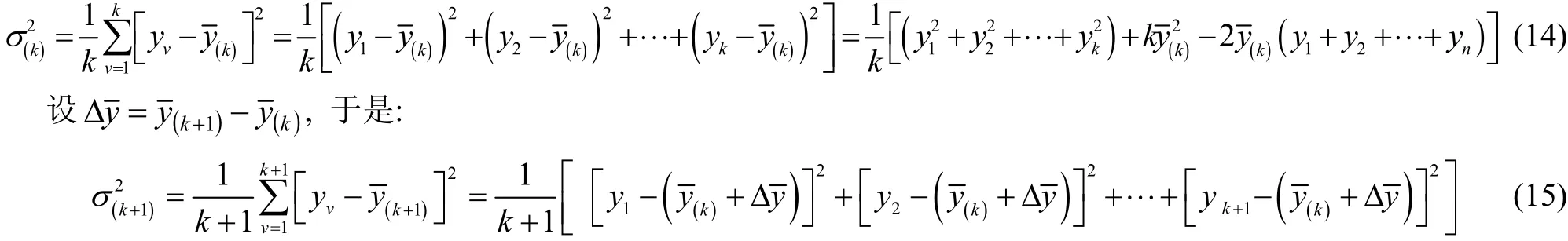
联合式(14),则从式(15)可得到如下的方差递推计算表达式

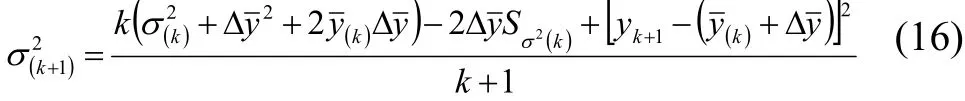
又由于:

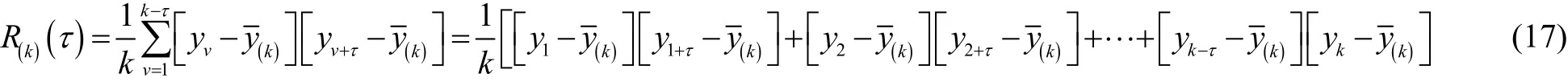
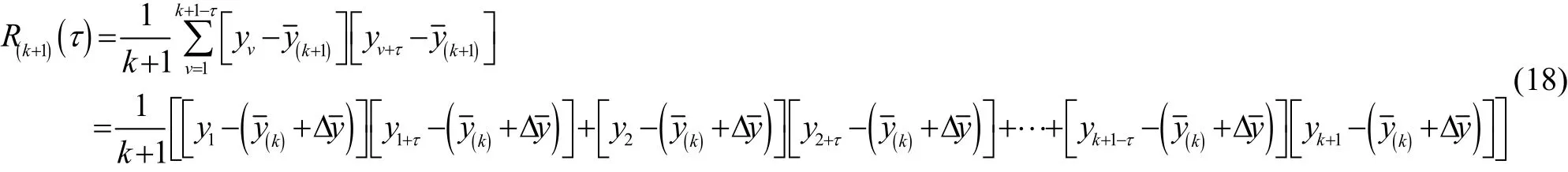
类似地,联合式(17),则可从式(18)得到如下的自 相关函数递推计算表达式:

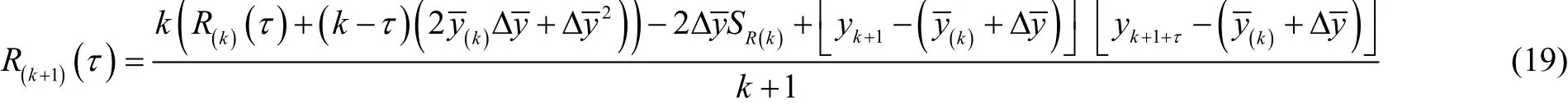
2)基于AR模型的各分段局部平稳时序数据的辨识

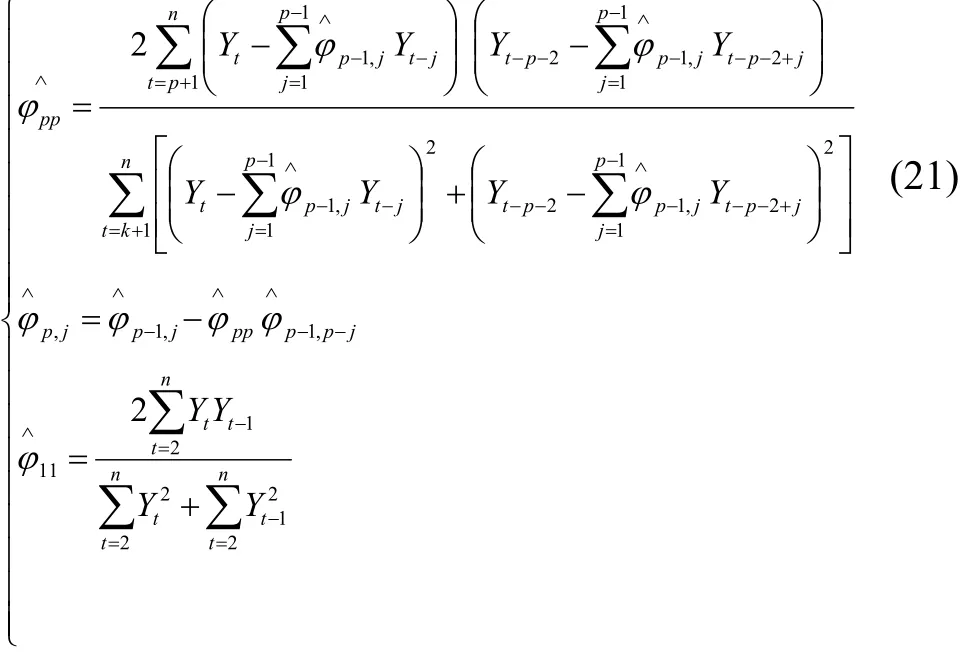
而模型阶次 p则可用式(22)所示的 FPE(Final Prediction Error)最小最终预报误差准则来确定[21].

3.2 算法的设计实现

综上所述,可设计如下的分段局部平稳时序数据的递推辨识算法.

步骤1.在Yt中析出各局部平稳子时序数据的分界点.

1)从Yt的最左端选取L个右邻样本数据构成Y1t子序列;

2)利 用 式 (4)～(6)计 算 Y1t对 应 的

3)往Y1t中添加Step个右邻样本数据并合并成子序列,利用式(13)、(16)、(19)递推计算Y2t对应的y

5)用式(7)～(9)对第Step点进行突变分界点判别,若第Step点为分界点,则保存分界点同时设置第Step点为Y1t子序列的左起点并跳转(1.2);否则,并跳转(1.3);若Yt遍历处理完毕后,跳转步骤2.

步骤2.依据步骤1中所得的各分界点,将Yt划分为数段局部平稳的子序列在此基础上,基于AR模型对各段局部平稳子序列进行辨识,辨识参数和模型阶次可由式(21)和式(22)得到.

步骤3.输出有关计算结果并结束算法.

4 实验及结果分析

为了验证上述算法的合理性及有效性,这里将对具有分段局部平稳的时序数据进行相关的辨识实验,实验的主要目的是对比本文算法与现有算法在辨识精度及计算效能上的差异.实验的硬件环境为惠普ProDesk 490 G2 MT商 用 台 式 机 (CPU:i5-45704*3.2GHz;内存:4GB DDR3 1600),软件环境及开发工具为Windows 8.1+Microsoft Visual C++2010.

4.1 实验设计

实验所用的模型如式(23)所示,如图1所示,该模型由3段样本长度均为100的局部平稳子序列组成.

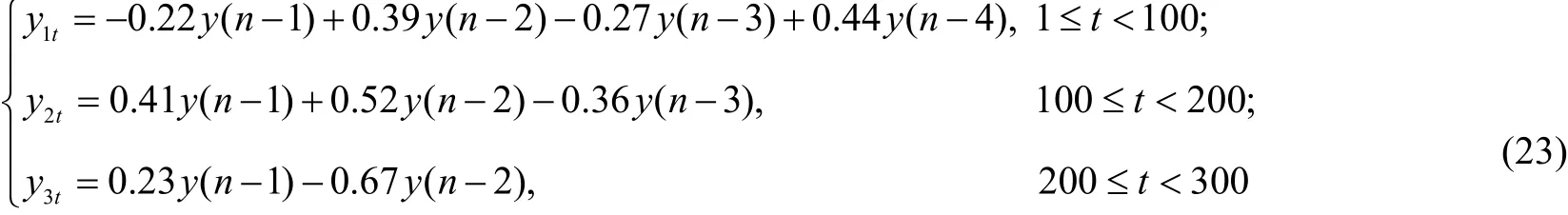
图1 由3段局部平稳子序列组成的实验模型

分别用文献[15]、文献[16]及本文的算法对式(23)进行相关辨识,辨识的任务为析出各局部平稳子序列的分界点,并确定这些子序列的模型阶次和辨识参数.

4.2 实验结果与讨论

如表1所示,文献[15]、文献[16]及本文的算法均能正确地从实验模型中析出3段局部平稳子序列;在分界点的划分精度问题上,文献[15]的算法在第1、2个分界点上分别偏离了实验模型1个和2个样本点,文献[16]的算法则分别偏离了4个和2个样本点,而本文的算法则分别偏离了8个和7个样本点,上述算法所析出分界点的误差范围均在10%以内.据此,应用均值、方差及自相关函数等数字统计特征对时序数据进行平稳性校验是有效的.对于各局部平稳子序列的模型阶次而言,上述算法均能正确地识别出与实验模型相一致的阶次.

表1 三种算法的辨识结果

分界点的析出偏差所引起的辨识精度问题,可用式(24)的平均绝对百分误差(MAPE,mean absolute percentage)来进行评价.如表2所示,文献[15]的算法的辨识精度最高,其次是文献[16]的算法,而本文的算法在辨识精度上略差于上述2种辨识算法,究其原因是因为在递推计算过程中本文算法存在着固有的积累误差,从而使得分界点的析出范围过大,并最终导致了Burg算法在模型参数估计时出现了一定的偏差.本文的算法的MAPE数值虽然比文献[15]和[16]的算法有所增加,但由于各辨识曲线的MAPE数值均没有超出10%,故本文的算法仍属于高精度辨识.

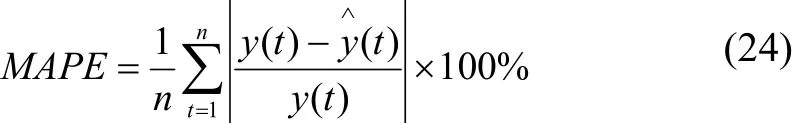
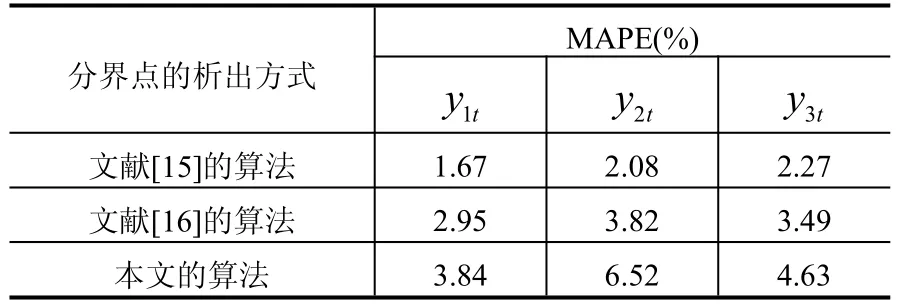
表2 三种算法的辨识精度评价

如表3所示,本文算法在辨识耗时上有了显著的提升,其计算效能较文献[15]和文献[16]的算法分别提升了约80%和70%.事实上,由于在分界点的析出过程中引入了递推机制,故本文算法的计算耗时主要是花费在各局部平稳子序列的模型定阶及模型参数估计的过程中;相对地,文献[15]和文献[16]的算法由于需要计算多维条件的分布概率来估计最优分界点,故它们的计算耗时主要是花费在分界点的析出过程中.

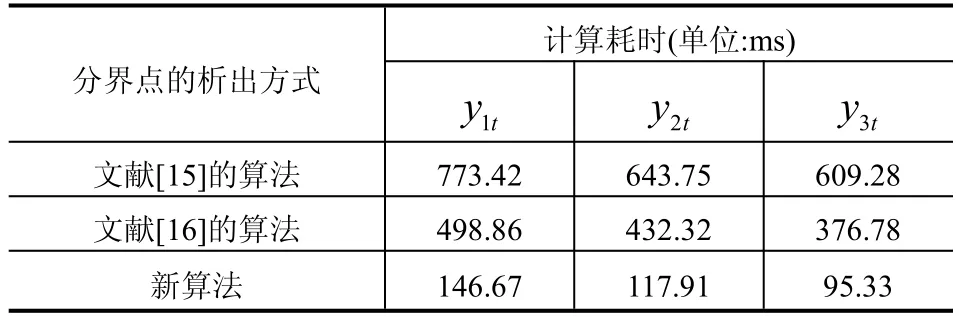
表3 三种算法的辨识耗时

从上述实验结果及分析中易知,本文提出的分段局部平稳时序数据的递推辨识算法是有效可行的,在保证高精度的辨识条件下,本文算法在计算效能取得了显著的提升.

5 结语

本文设计实现了一种具有递推机制的分段局部平稳时序数据的辨识算法,并就算法的辨识精度和计算效能进行了深入的分析.下一步的主要工作有,设法减少递推过程中的积累误差,以便更精确地析出各局部平稳时序数据的分界点;同时,研究各分段局部平稳时序数据的并行辨识问题,从而更好地提升算法的计算效能.

1张贤达.用高阶累量辨识MA系统的新方法.电子学报, 1994,22(10):27–33.

2王正明,易东云.含ARMA噪声系统模型的参数辨识方法,控制理论与应用,1996,13(8):471–475.

3熊渊博.ARMA模型参数的分步估计方法.湖南大学学报(自然科学版),2003,30(2):12–15.

4周毅,丁锋.依等价AR模型阶次递增的自回归滑动平均模型辨识.华东理工大学学报(自然科学版),2008,34(3): 425–431.

5张新广,李志农,王心怡,等.一种基于阶比域的AR模型盲辨识算法.振动与冲击,2009,28(5):41–43.

6博克斯,詹金斯,莱因泽尔.时间序列分析:预测与控制.北京:机械工业出版社,2011.

7 Matilainen M,Nordhausen K,Oja H.New independent component analysis tools for time series.Statistics& Probability Letters,2015:80–87.

8 Yin Y,Shang PJ,Xia JN.Compositional segmentation of time series in the financial markets.Applied Mathematics and Computation,2015:399–412.

9 Bernas M,Płaczek B.Period-aware local modelling and data selection for time series prediction.Mechanical Systems and Signal Processing,2016:60–77.

10王宏禹,邱天爽,陈喆.非平稳随机信号分析与处理.北京:国防工业出版社,2008.

11 Spiridonakos MD,Fassois SD.Adaptable functional series TARMA models for non-stationary signal representation and their application to mechanical random vibration modeling.Signal Processing,2014:63–79.

12朱学锋,韩宁.基于小波变换的非平稳信号趋势项剔除方法.飞行器测控学报,2006,25(5):81–85.

13林树宽,杨玫,乔建忠,等.一种非线性非平稳时间序列预测建模方法.东北大学学报(自然科学版),2007,28(3): 325–328.

14 DjuricPM,Kay SM.FayeBoundreaux-BartelsG. Segmentation of nonstationary signals.Proc.of the IEEE ICASSP.1992.161–164.

15王文华,王宏禹.分段平稳随机过程的参数估计方法.电子科学学刊,1997,19(5):311–317.

16陈颖,李在铭.一种改进的分段平稳随机过程的参数估计方法.电子与信息学报,2003,25(6):735–740.

17金连文,韦岗.现代数字信号处理简明教程.北京:清华大学出版社,2003.

18杨叔子,吴雅,轩建平,等.时间序列分析的工程应用(上册).武汉:华中科技大学出版社,2007.

19项静恬.动态数据处理-时间序列分析.北京:气象出版社,1986.

20黄雄波.时序数据的周期模式发现算法的递推改进.计算机技术与发展,2016,26(2):47–51.

21克西盖斯纳,沃特斯,哈斯勒.现代时间序列分析导论.北京:中国人民大学出版社,2015.

SegmentedIdentification and RecursiveAlgorithm forNon-StationaryTime Series Data

HUANG Xiong-Bo

(Department of Electronic and Information Engineering,Foshan Professional Technical College,Foshan 528137,China)

In fact,there widely exists a kind of time series data that is non-stationary but can be transformed into several local stationary time series data,the identification problem of the non-stationary time series data is studied,and then this paper proposes a piecewise recursive identification algorithm with mechanism.Based on the definition of stationary time series data,the precipitation algorithm which has the mean variance point,the mutation point and the mutation point of the autocorrelation function,is constructed based on the statistical characteristics such as the mean and variance and autocorrelation function.On this basis,a series of locally stationary sub sequences are identified from the identified non-stationary sequences,and then,the Burg algorithm is applied to the recursive identification of local stationary subsequences.The experimental results show that the new algorithm can divide the boundary points of the local stationary sub sequences with smaller position deviation.At the same time,the calculation efficiency is improved significantly under the condition of high accuracy.

non-stationary time series data;local stationary;segmented identification;recursion;demarcation point; auto-regressive model

广东省科技计划工业攻关项目(2011B010200031);佛山职业技术学院校级重点科研项目(2015KY006)

2016-08-14;收到修改稿时间:2016-10-19

10.15888/j.cnki.csa.005772