K-means算法初始聚类中心选择的优化①

郁启麟

(中国矿业大学 计算机科学与技术学院,徐州 221116)

K-means算法初始聚类中心选择的优化①

郁启麟

(中国矿业大学 计算机科学与技术学院,徐州 221116)

迄今为止,在数据挖掘领域,人们已经实现了多种聚类算法,其中使用最广泛的当属K-means聚类算法.然而,在数据挖掘中,K-means算法面临的一个主要问题就是初始中心点选择问题.本文提出了一种结合关系矩阵和度中心性(Degree Centrality)的分析方法,从而确定K-means算法初始的k个中心点.与传统方法相比,本文算法可得到更加优质的聚类结果.实验结果表明该算法的有效性和可行性.

数据挖掘;度中心性;K-means算法;聚类

1 引言

随着互联网的不断发展,人们已经进入到了大数据时代,并且已经真正体会到无边际的海量数据.数据挖掘技术的实现,使人们可以利用这些海量数据,发掘出可供人们决策的知识.现有的数据挖掘方法有多种,主要包括关联规则分析、聚类分析、离群点分析、分类等.其中聚类是一种无监督学习的分类技术,聚类的目的是使同一类中的数据的相似度尽可能高,而且不同类的相异度也尽可能高.从而得到数据中潜在的分类信息.

主要的聚类算法有:基于划分方法、基于层次方法、基于密度方法、基于网格方法和基于模型方法. K-means算法是一种基于划分的聚类分析方法,该算法的运行效率较高,因此广泛应用于各个领域的聚类分析中,目前的许多算法都是围绕着它进行创新和拓展.但是,在传统的K-means聚类分析中存在很多缺陷:(1)在K-means算法中,k是需要事先给定的.(2)在K-means算法中,初始中心的选择对聚类结果影响比较大,若初始聚类中心选择的不合适,那么就无法得到预期的聚类结果,这也是K-means算法的一个缺点. (3)一些噪声点和孤立点会对最终的聚类结果产生较大的影响.

目前,针对以上K-means算法的缺点,很多学者提出了对K-means算法的优化方法,如文献[1]采用密度敏感的相似性度量计算对象密度的方法产生初始类中心,从而优化聚类结果的稳定性;文献[2]提出一种基于人工鱼群的优化算法AFS-KM,利用信息增益对属性进行加权,从而计算实体之间的距离.文献[3]通过找出相距最远的数据对象作为初始聚类中心,然后对该聚类进行分裂,反复迭代直到找出指定个数的初始聚类中心;文献[4]结合Ap算法和最大最小距离算法确定K-means算法的最佳聚类个数.文献[5]利用大数据技术,结合Hadoop平台的map和reduce框架优化K-means算法;文献[6]提出了一种新的NDK-means方法,它通过标准差确定有效密度半径,然后挑取高密度区域中的具有代表性的样本点,用这些样本点作为初始聚类中心;文献[7]基于结果敏感性和局部最优而提出了一种K-meansCAN算法,利用不同聚类结果的子簇的交集建立带权连通图,根据图中各节点的连通性合并子簇;文献[8]将K-means算法和蚁群算法相结合,提高了聚类质量;文献[9]采用密度方法和对象间的距离确定初始聚类中心,选择相距最远的k个处于高密度区域的点作为初始聚类中心.文献[10]利用核系数解决非凸问题,确定合适的聚类个数.文献[11]利用最大最小距离算法,根据已经选取到的中心点,选取与之距离乘机最大的的高密度点作为当前初始中心点.

本文在研究K-means算法及其一些改进算法的基础上,提出一种新的选取初始聚类中心的方法,该方法与关系对称矩阵和度社会网络分析中的度中心性相结合确定初始聚类中心,将所得到的聚类中心应用于聚类算法当中,在稳定聚类结果的同时,使得聚类结果有了较大提高.

2 K-means算法简介

K-means算法根据聚类的个数k,将已有的数据集划分成k个簇.算法采用迭代更新的方法,在第一轮中,根据随机选定的k个初始中心点将对象集划分成k个初始簇,之后根据每个簇的中心迭代重新划分每个对象所属的类,而每个簇的平均值将被作为下一轮迭代的中心点.直到中心点不再发生改变,即产生了最后的聚类结果.

2.1 K-means算法的主要步骤

假设将数据集D包含n个数据对象.该算法将D中的对象分配到k个簇W1,W2…WK中,每个簇的中心设为c1,c2…ck,其中,其中是簇中数据点的个数.对象与该簇的代表之间的欧式距离用dist(x,ci)表示,聚类效果的好坏用目标函数目标函数E就是每个数据点与其所在簇的簇中心的距离总和,随着聚类次数不断增加,E值也会动态的改变,理想状况下,E值会逐渐收缩变小,簇内对象的相互距离会变小,簇间的相互距离会逐渐变大.因此,算法通过不断寻求更加小而稳定的E值来寻求好的聚类方案,当E逐渐收缩到极小值时,会产生更好的聚类结果.

2.2 K-means算法描述

3 度中心性简介

度中心性(Degree Centrality)是在社会网络分析中分析节点在整个网络中重要程度的一个很重要和直接的方法.与一个节点相连接的其他节点个数越多,就表示这个节点的度中心性越高,那么这个节点在网络中的重要性就越高.

在拥有N个节点的无向图G中,节点i的度中心性表示该节点与其它N-1个节点的联系程度.即用于计算节点i与其它N-1个节点的直接连接数量,i≠j表示节点自身与自身的连接可以忽略不计.度中心性的计算可以简单地将节点i在矩阵中对应的行或列所在的单元格值加总.

度在有向网络图中分为入度和出度,例如微博中的关注关系.因为本文将相互距离小于阈值的两个节点看作是相互连接的,所以关系对称矩阵转化为无向图,不区分出度和入度.

4 初始中心点的确定

针对初始中心点对聚类结果的影响,本文提出了一种基于在关系矩阵中测量度中心性的方式优化初始中心点的选择.首先,将对象集N内的节点计算两两之间的距离,因为不同的距离计算方法不会对本算法造成大的影响,所以为了降低计算量,本文采用曼哈顿距离.设立一个阈值L,根据反复测试,L取任意两个节点之间平均距离的一半.两个节点之间的距离如果小于这个阈值,建立节点之间的关系对称矩阵时,我们将值设置为1,即认为这两个节点在网络中是相互连接的;如果距离大于阈值,则设为0,即认为这两个节点在网络中是无连接的.遍历所有对象的行向量,将度中心性最高的节点设为初始中心点,并将与之相连的节点从矩阵中删除.继续迭代遍历剩下的节点,直到找到k个中心点.

设目标对象集N={X1,X2,X3,…Xn},包含n个对象,每个对象有m个属性,设每个对象Xi={xi1,xi2,…xim},从数据集N中选出k个中心点.

算法描述如下:

(1)预处理数据集N.

(4)遍历所有节点,找出度中心性最高的节点,然后在矩阵中删除该节点,由于类中心点相互之间的距离应该尽可能远,且相互连接的节点是抱团存在的,所以删除与之相连接的p个节点,所以n阶矩阵转变为n-p+1阶矩阵.

(5)在形成的新矩阵中继续找出度中心性最高的节点,设为第2个中心点,并在方阵中删除与之相连接的节点.利用迭代算法继续循环遍历直到找出第k个中心点.

5 实验仿真分析

图1为本文算法的流程图.为了方便计算,并能表示出原始算法与改进算法的区别,所以本文使用java语言随机生成7维的仿真数据对象,因为现实数据中每一维的差距有限,所以将每一维的属性用0-200的整数型数字表示.并用java语言生成对象对称关系矩阵.分别用原始方法选择的初始中心点和本方法选择的初始中心点比较聚类过程消耗的时间和聚类最终的效果.

图1 实验流程图

图2 为选取的前10个节点根据相互之间的距离和阈值L转化而成的0和1的关系对称矩阵,由于是无向图,本文这里将节点本身看作是有连接的,这样对最终的初始中心点选取结果并不会产生影响.

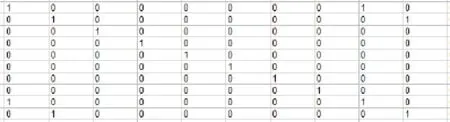
图2 选取10个节点的关系矩阵

图3 表示100个节点利用如图2所示的关系对称生成的社会网络关系图.我们可以很明显的看出相互之间距离小且连接的节点是抱团存在的;又因为选取的初始中心点距离应该尽可能的远,所以我们在选取每个初始中心点后,因为与之相邻的节点将不会作为我们选取下一个聚类中心的候选节点,所以我们在矩阵网络中删除与之相邻的节点.

图3 包含100个节点的网络连接图

本文为了更准确的表示比较结果,所以将每种算法反复运行30次,用最终的四舍五入后的平均值去表示实验性能和结果.以下实验结果均为反复测试的平均值.

表1表示在没有离群点的对象集中测试的实验结果,本文使用两种方法的运行时间和E值来作为衡量指标.这里的E值表示所有节点与最终所在的簇中心距离之和,E值的大小体现了最终子簇成员之间的紧密程度.

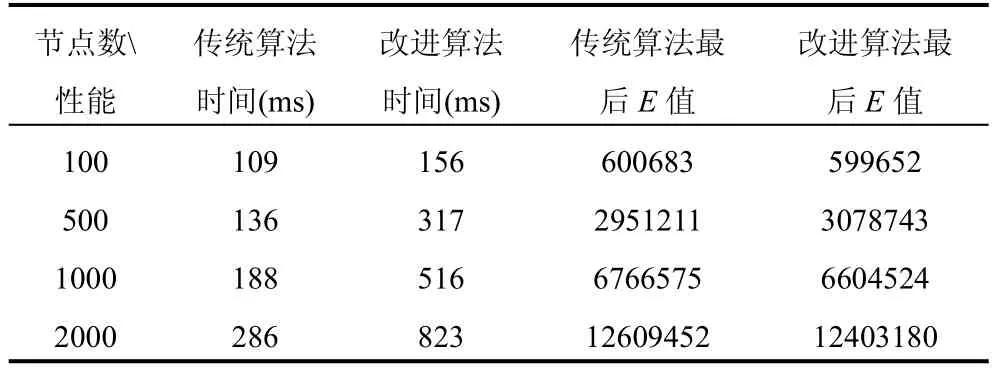
表1 不包含离群点的实验结果

表2表示在含有离群点的对象集中分别使用两种方法的运行时间和E值对比,为了说明改进算法的有效性,我们将添加的离群点设为原算法的其中一个初始中心点.

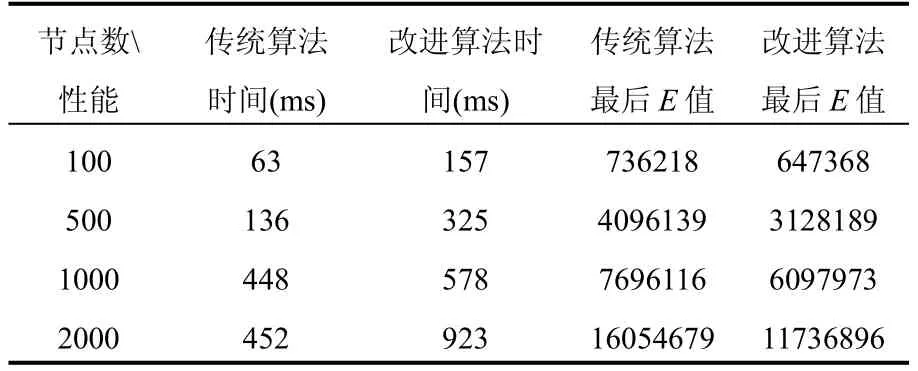
表2 包含离群点的实验结果

除了与传统方法比较之外,本文还与最新的文献中的改进方法进行比较,本文选取了文献[1],文献[3]和文献[6]中的优化初始中心选取方法进行实验比较,实验中使用了包含离群点的500个实验对象,并且使用经过反复实验得到的理想K值,用运行时间、迭代次数和E值来表示实验结果,比较结果如表3所示.

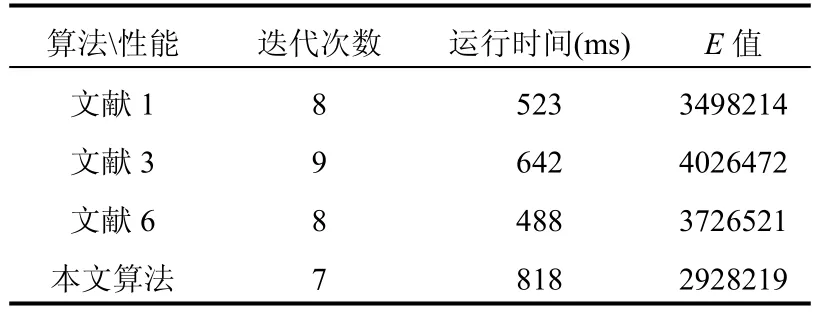
表3 与近期改进算法的比较结果

通过表1和表2我们可以看出,在平滑的数据集中进行聚类处理,改进的算法与传统算法在时间性能上的聚类结果上没有优势,但是在含有离群点数据集中,改进的算法的聚类结果明显优于传统算法.

通过表3可以看出,本文中提出的算法与近期文献提出的方法相比较而言,本文提出的改进算法在时间性能上有一定的劣势,但是在类内距和迭代次数这两个指标上优于近期文献中提出的算法,可以产生更加稳定和优质的聚类结果.

通过以上实验结果可以得出结论,由于本文中提出的算法在聚类之前要生成对称矩阵,并且要迭代计算每个节点的度中心性,所以造成了大量的时间消耗,但是通过这种方式可以找到更加优质的初始聚类中心,从而能够生成更加精确和稳定的聚类结果,所以本文提出的算法更适合体量小的聚类对象集,在实际应用中是可行的.

6 结语

传统的K-means算法在进行聚类时随机的选取对象集合中的k个点作为初始聚类中心,这导致了该算法失去了稳定性,容易产生不理想的结果.本文提出了一种利用关系矩阵和度数中心度的方法去优化K-means算法中的初始中心节点选择问题,得到了更加优化的初始中心点.本文通过用java代码生成的测试对象集和运行代码,通过与传统方法以及最新的改进算法进行比较,证明了本算法的高稳定性.虽然生成矩阵的过程造成了大量的时间消耗,在处理海量数据的性能上有一定的局限性;但是从一方面讲,本算法又减少了聚类过程中的迭代次数,得到更加稳定和高质量的聚类结果,所以这些代价是在实际应用中是可以付出的.今后也会进一步完善本文提出的算法.

1汪中,刘贵全,陈恩红.一种优化初始中心点的K-means算法.模式识别与人工智能,2009,22(2):299–304.

2于海涛,贾美娟,王慧强,等.基于人工鱼群的优化K-means聚类算法.计算机科学,2012,39(12):60–64.

3陈光平,王文鹏,黄俊.一种改进初始聚类中心选择的K-means算法.小型微型计算机系统,2012,33(6):1320–1323.

4周世兵,徐振源,唐旭清.新的K-均值算法最佳聚类数确定方法.计算机工程与应用,2010,46(16):27–31.

5赵庆.基于hadoop平台下的k均值高效算法的研究[硕士学位论文].西安:西安电子科技大学,2014.

6何云斌,刘雪娇,王知强,等.基于全局中心的高密度不唯一的K-means算法研究.计算机工程与应用,2016,52(1):48–54.

7雷小锋,谢昆青,林帆,等.一种基于K-Means局部最优性的高效聚类算法.软件学报,2008,19(7):1683–1692.

8莫锦萍,陈琴,马琳,等.一种新的K-Means蚁群聚类算法.广西科学院学报,2008,24(4):284–286.

9赖玉霞,刘建平.K-means算法的初始聚类中心的优化.计算机工程与应用,2008,44(10):147–149.

10 Yu S,Tranchevent LC,Moor BD,et al.Optimized data fusion for Kernel k-means clustering.IEEE Trans.on Pattern Analysis&Machine Intelligence,2012,34(5): 1031–1039.

11 Li MJ,Ng MK,Cheung YM,et al.Agglomerative fuzzy k-means clustering algorithm with selection of number of clusters.IEEE Trans.on Knowledge&Data Engineering, 2008,20(11):1519–1534.

Optimization of Initial Clustering Centers Selection Method for K-MeansAlgorithm

YU Qi-Lin

(School of Computer Science and Technology,China University of Mining and Technology,Xuzhou 221116,China)

So far,in the field of data mining,people have achieved a variety of algorithms of clustering.And the most widely used is K-means clustering algorithm.But the main problem of K-means is the initial center selection problem. In this paper,a method is proposed to determine the initial K centers of the K-means algorithm through the relationship matrix and the Degree Centrality.Compared with the traditional algorithm,the proposed algorithm can get the better clustering result.Experimental results have proved the validity and feasibility of this algorithm.

data mining;degree centrality;K-means algorithm;clustering

2016-08-01;收到修改稿时间:2016-09-23

10.15888/j.cnki.csa.005733