基于RV减速器有限元装配模型的摆线轮受力分析
2017-06-06吴鑫辉刘珂荧冯长建李文龙
吴鑫辉,刘珂荧,冯长建,李文龙
(1.大连民族大学 机电工程学院,辽宁 大连 116605;2. 大连工业大学 机械工程与自动化学院,辽宁 大连 116034)
基于RV减速器有限元装配模型的摆线轮受力分析
吴鑫辉1,刘珂荧2,冯长建1,李文龙1
(1.大连民族大学 机电工程学院,辽宁 大连 116605;2. 大连工业大学 机械工程与自动化学院,辽宁 大连 116034)
以工业机器人普遍采用的RV减速器为研究对象,通过考虑RV减速器第一级传动中太阳轮和行星轮变形,第二级传动中针齿壳、针齿、摆线轮、曲柄轴承滚子和曲柄轴变形,针齿和针齿孔加工误差,曲柄轴承间隙及摆线轮与针齿间啮合侧隙,基于有限元法,利用ANSYS APDL建立RV减速器参数化有限元装配模型。通过有限元仿真分析得出各因素综合作用下摆线轮齿受力分布及各齿受力大小,总结出摆线轮轮辐结构变形对摆线轮受力的影响规律,为RV减速器摆线轮结构参数优化提供依据。
RV减速器;有限元装配模型;对摆线轮受力的影响规律;摆线轮;受力分析
随着工业机器人用RV(Rotate Vector)减速器朝着轻量化的方向发展,摆线轮重量更轻,尺寸更小,轮辐结构柔性更大。现有关于RV减速器摆线轮受力分析的理论大部分都是假设摆线轮为刚体,根据赫兹接触理论计算摆线轮齿接触齿数和各齿受力大小[1]。据RV减速器的有限元分析结果显示,摆线轮的最大变形量达到十几微米,因此为了准确分析摆线轮受力,必须考虑摆线轮变形。孙宇[2]通过Pro/E进行摆线轮实体建模,利用ANSYS进行有限元分析,分析中将三维模型简化为平面模型,对摆线轮单独进行有限元分析;张东生[3]基于传统受力分析理论,通过MARC软件对一片摆线轮和针齿壳进行二维接触分析;吴素珍[4]基于摆线针轮行星传动的啮合原理,采用有限元法建立了RV减速器中摆线针轮传动的有限元模型,分析摆线轮接触应力;戴文婷[5]在SolidWorks软件环境下,建立了摆线轮的有限元模型,分析了摆线轮与针轮在输出轴回转一周的过程中接触应力的变化规律。Shuting Li[6]利用有限元方法进行负载工况下摆线轮接触分析,以解决摆线针轮减速器受力分析与评价的问题,并基于这个模型开发了有限元软件,从而可以很好地分析摆线轮齿、轴承滚子和柱销的接触力和接触应力分布,也能分析摆线轮的弯曲应力。Blagojevic′ M.和Marjanovic′ N.等[7]利用有限元法分析摆线针轮减速器的应力和应变情况。Thube S.V. 和Bobak T.R.[8]采用有限元法对包含针齿、单片摆线轮和行星架的简单摆线针轮减速器进行分析,研究摆线轮上的应力和变形在一定仿真时间内的变化规律。RV减速器中摆线轮结构与传统摆线针轮减速器中摆线轮结构不同,本文考虑关键零部件变形、加工误差和轴承间隙三个因素,通过ANSYS APDL建立RV减速器参数化有限元装配模型,从而分析摆线轮受力情况。
1 建立有限元模型
1.1 基本参数
RV减速器基本参数见表1,零件材料属性见表2。

表1 RV减速器基本参数

表2 零件材料属性
1.2 摆线轮模型建立及装配
机器人用RV减速器是高精密减速器,对建模精度要求很高,本文建模时对摆线齿形曲线进行了精确计算,使其齿形曲线误差保持在0.3 μm以下,模型如图1。

图1 摆线轮齿形曲线
为将摆线轮齿网格划分为六面体,分别建立摆线轮齿与摆线轮轮辐模型,摆线轮齿网格模型如图2。由于摆线轮的齿缘较薄,变形比较大,对摆线轮受力有直接影响,因此按图纸尺寸准确建立摆线轮轮辐实体模型,网格模型如图3。

图2 摆线轮齿网格模型

图3 摆线轮轮辐网格模型
由于摆线轮轮辐与摆线轮齿有限元模型是分别建立的,网格节点不连续,本文采用耦合和约束方程的方法将两个具有不同网格特征的区域连接起来,如图4。在轮齿接触区域内按最大接触跨齿数(14个)设计摆线齿,两片摆线轮装配模型如图5。

图4 摆线轮齿与轮辐耦合模型

图5 两片摆线轮装配模型
1.3 针齿壳及针齿模型建立及装配
为了在不影响计算精度的前提下尽量减少计算时间,把针齿壳简化成为一个圆柱体,其中针齿孔的直径为(7+0.004)mm,在轮齿接触区域内按最大接触跨齿数设计14个针齿孔。按平均误差选取针齿直径为(7-0.004)mm。为了更好地观察摆线轮的变形等对接触状态的影响,建模时没有计入针齿的综合周节误差[9]。针齿与针齿孔接触区域为复杂应力梯度区域,网格需要细化。采用约束方程将针齿和针齿孔连接起来如图6,针齿壳与摆线轮装配模型如图7。
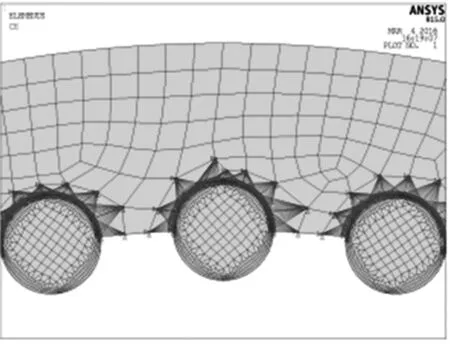
图6 针齿壳和针齿耦合模型
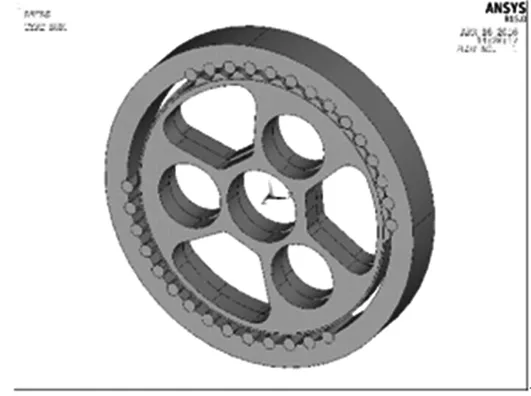
图7 针齿壳和摆线轮装配模型
1.4 曲柄轴承模型建立
曲柄轴承的滚柱直径为5 mm,宽度为8 mm,14个滚柱均匀分布,轴承径向间隙取0.012 mm(按平均误差估计半径间隙0.006 mm),如图8。
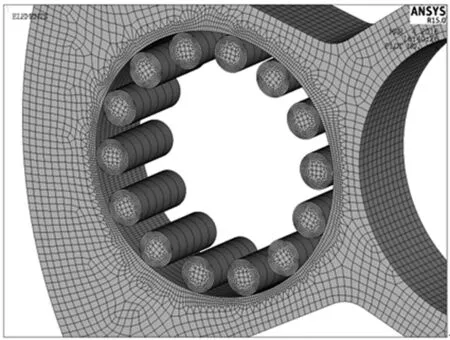
图8 曲柄轴承滚子网格模型
1.5 曲柄轴模型建立及装配
曲柄轴为3个,两偏心凸轮用约束方程约束在曲柄轴上。曲柄轴的网格模型如图9,装配后模型如图10。

图9 曲柄轴网格模型

图10 装配模型
1.6 第一级渐开线齿轮模型建立
第一级由一个太阳轮轴和三个行星轮构成,为尽量压缩运算时间,太阳轮只建立16个齿中的9个,每个行星轮只建立32个齿中的3个,太阳轮轴截掉轴段,行星轮通过约束方程固连在曲柄轴上。第一级齿轮网格模型如图11,装配后模型如图12。

图11 太阳轮和行星轮网格划分
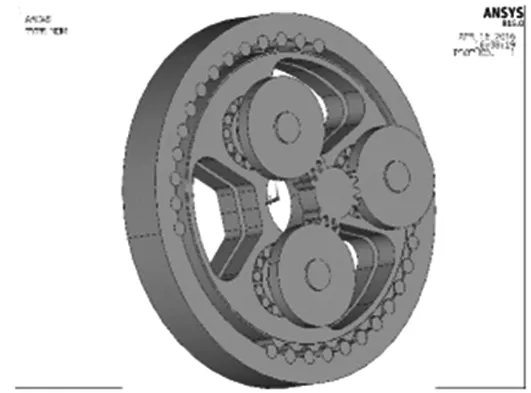
图12 装配模型
1.7 RV减速器有限元装配模型建立
由于行星架刚性较大,将行星架作为一个刚性点,点的单元属性为MASS21,并用CERIG命令将该点与偏心轴中心各节点刚性连接以代替行星架。RV减速器有限元装配模型各部件约束关系见表3,零部件接触关系见表4。

表3 RV减速器有限元装配模型各部件约束关系

表4 RV减速器有限元装配模型零部件接触关系
RV减速器有限元装配模型共包含158个实体,1 227 915个节点,1 006 668个单元,如图13。

图13 RV减速器有限元装配模型
2 RV减速器摆线轮受力分析
通过有限元分析得出输入端摆线轮和输出端摆线轮的传递转矩见表5。

表5 两片摆线轮分别传递的转矩
输入端摆线轮与输出端摆线轮所传递转矩不相同,这是由于针齿和针齿孔加工误差及轴承间隙等因素影响的结果,与工程实际相符。选取输出端摆线轮作为研究对象,摆线轮接触应力分布如图14,各齿所受接触力大小见表6。
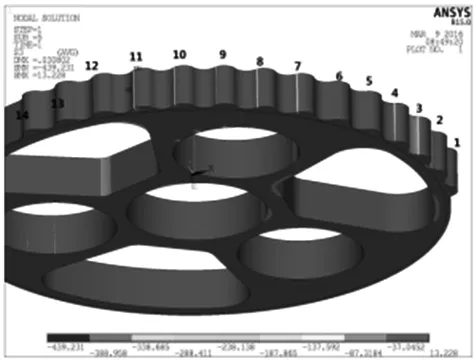
图14 摆线轮接触应力分布图

齿号1234567接触力/N00603.39533.59107.1501023.00齿号891011121314接触力/N801.00470.19924.301554.40524.1900
提取2、5、6号齿在1 s内所受啮合力随时间变化曲线,如图15。

图15 2、5、6号齿啮合力时变曲线图
2、5、6号齿啮合位置所处的齿廓段采用负等距修形,补偿了由于针齿和针齿销孔加工误差及曲柄轴承间隙引起的针齿与摆线轮齿之间的间隙。开始时啮合力为零,在0.3 s前,2号齿所处的摆线轮轮缘未产生变形,随着加载时间的增加,啮合力随着齿面变形量的增大而增大;当加载到0.3 s时,齿面变形量达到最大值,同时摆线轮轮缘开始变形,此时2号齿与针齿之间的间隙随着轮缘的变形而逐渐增大,2号齿的啮合力随之减小;当加载到0.8 s时,轮缘的变形使得2号齿与针齿脱离接触,2号齿啮合力为零。6号齿受力规律与2号齿基本相同,但5号齿由于所处的轮缘刚度大于2号齿,在加载0.6 s时,5号齿所处的轮缘开始产生变形,使得5号齿与针齿间的间隙增大,齿面变形量减小,啮合力减小。由于2、5、6号齿的啮合位置位于靠近齿根处,接触压力角大,啮合力较小。
提取10、11、12号齿在1 s内所受啮合力随时间变化曲线,如图16。

图16 10、11、12号齿啮合力时变曲线图
由于针齿及针齿销孔加工误差及曲柄轴承间隙的影响,10、11、12号齿在开始时与针齿间存在间隙,当加载到0.2 s时,10、11、12号齿与针齿接触,随着加载时间的增加,齿面变形量增大,啮合力增大。这三个齿的啮合力变化规律基本相同。
为了方便说明,定义摆线轮梯形孔上方区域为柔性区,因为该区域比较薄弱,转臂轴承孔两侧由于有类似加强筋的结构,所以刚性大,将此区域定义为刚性区,如图17。
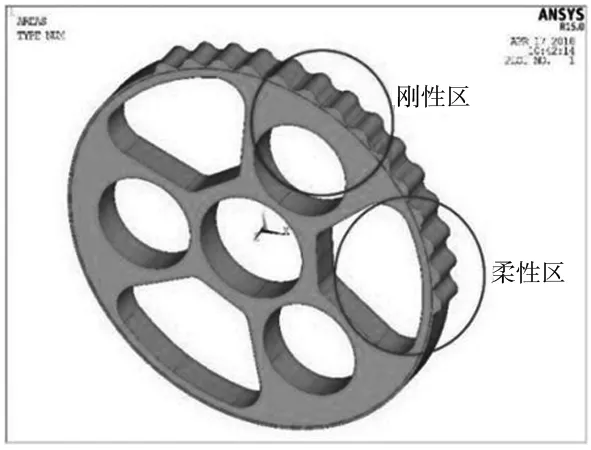
图17 刚性区和柔性区的定义
将摆线轮变形放大300倍,如图18。
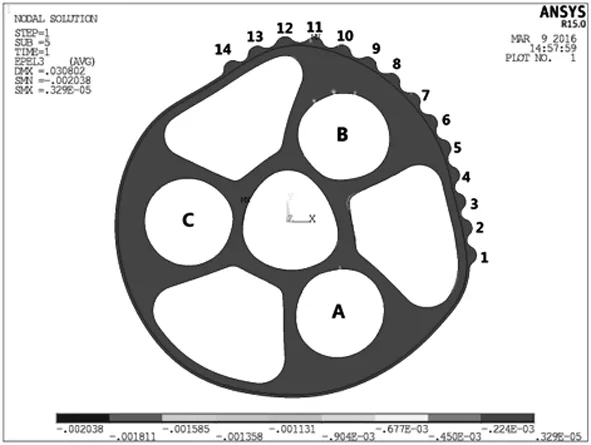
图18 摆线轮变形放大300倍图
由图中可以看出:1、2、3、4号齿分布在柔性区,在针轮及A、B、C三处曲柄轴的共同作用下,该柔性区相对于刚性B区沿顺时针方向被拉伸,产生凹陷变形,柔性区1、2、3、4号齿及邻近的5、6号齿与针齿间啮合间隙增大,啮合力减小;12、13、14号齿所在的柔性区相对于刚性B区沿顺时针方向被压缩,也产生凹陷变形;7、8、9、10、11号齿所在的刚性B区相对于12、13、14号齿所在的柔性区沿逆时针方向被压缩,整个刚性区产生外凸变形,其中11号齿作为柔性区和刚性区的过渡齿,外凸变形最大,受力最大,与11号齿相邻的10号齿和12号齿随着外凸变形的增大,啮合力逐渐增大。这样刚性区的齿承受主要载荷,柔性区的齿受力较小或不受力,从而降低摆线轮柔性区的疲劳破坏。
3 结 论
(1)本文建立了考虑针齿及针齿孔加工误差和曲柄轴承间隙的RV减速器有限元装配模型,利用该模型可以高效、准确地分析摆线轮的受力情况。
(2)归纳总结出摆线轮变形对摆线轮齿受力的影响规律,受力最大的齿是相互压缩的刚性区和柔性区的过渡齿,刚性区分布的齿承受主要载荷,柔性区分布的齿受力较小或不受力,以降低摆线轮柔性区的疲劳破坏。
[1] 李力行.摆线针轮行星传动的齿形修正与受力分析[J].机械工程学报,1986(1):18-23.
[2] 孙宇.摆线针轮行星减速器的有限元分析研究[D].陕西:西北农林科技大学,2008.
[3] 张东生.FA传动齿形优化和齿面接触状态有限元分析[D].大连:大连铁道学院,2004.
[4] 吴素珍,何卫东.RV针摆传动齿面接触强度非线性分析[J].郑州大学学报,2015,36(4):100-104.
[5] 戴文婷.摆线针轮减速器实体建模和啮合特性分析[D]. 天津:天津大学,2013.
[6] SHUTING L. Design and strength analysis methods of the trochoidal gear reducers[J]. Mechanism and Machine Theory, 2014, 81:140-154.
[7] BLAGOJEVIC′ M , MARJANOVIC′ N , DJORDJEVIC′ Z , et al. Stress and strain state of cycloid discs[C]. 1st International Scientific Conference on Mechanical Engineering Technologies and Applications, Jahorina, 2012: 367-374.
[8] THUBE S V,BOBAK T R. Dynamic analysis of a cycloidal gearbox using finite element method[J]. AGMA Technical Paper, Sumitomo Drive Technologies, 2012.
[9] 何卫东,吴鑫辉,卢琦.RV传动中摆线轮及曲柄轴承有限元分析[J].大连交通大学学报,2016(4):67-71.
(责任编辑 赵环宇)
Force Analysis of Cycloidal Gear based on the Finite Element Assembly Model of the RV Reducer
WU Xin-hui1, LIU Ke-ying2, FENG Chang-jian1, LI Wen-long1
(1.School of Electromechanical Engineering, Dalian Minzu University, Dalian Liaoning 116605, China;2.School of Mechanical Engineering and Automation, Dalian Polytechnic University, Dalian Liaoning 116034, China)
Taking the RV reducer which is widely used in industrial robots as the research object, considering the deformation of the sun gear and planetary gears in the first stage, the deformation of the needle shell, needle, cycloidal gears, crank bearing rollers and crankshaft in the second stage, machining errors of the needle and needle hole, crank bearing clearance and meshing backlash between cycloidal gear and pin gear, ANSYS APDL was used to establish the parametric finite element assembly model of the RV reducer based on the finite element method. Through the finite element simulation analysis, the force distribution of the cycloidal gear teeth and the force of each tooth are obtained under the combined effects of each factor, and the influence of the deformation of the cycloidal spoke on the force of the cycloidal gear is summarized, which provides the basis for the optimization of the structural parameters of the cycloidal gear in the RV reducer.
RV reducer; finite element assembly model; influence on the force of the cycloidal gear; cycloidal gear; force analysis
2017-03-13;最后
2017-03-26
国家自然科学基金项目(51375064)。
吴鑫辉(1987-),男,山西运城人,讲师,博士研究生,主要从事现代机械传动研究。
2096-1383(2017)03-0222-05
TH132.41
A
