帮你归纳—幂函数图象

云南省红河州蒙自市蒙自一中(新校区)(661100)

苏保明●



帮你归纳—幂函数图象

云南省红河州蒙自市蒙自一中(新校区)(661100)

苏保明●

幂函数是初等函数的重要内容之一，同时也是高考命制题型的重要内容，其中主要体现在对幂函数图象的考查，而高考题呈现方式却是对幂函数与其他函数图象的综合考查.由于幂函数图象的多样性和复杂性，导致给同学们带来学习上的一些困难，为了帮助同学们更好地学习幂函数的图象，本文对幂函数的图象进行了综合归纳，希望能对同学们的学习有所帮助.

知识回顾：形如y=xα(α∈R)的函数称为幂函数，其中x是自变量，α为常数，所有的幂函数在(0，+∞)都有定义，并且图象都过定点(1，1).幂函数随着α的不同，其定义域、值域都会发生变化，从而其图象也随之发生变化，根据幂函数的性质得出图象可归纳为以下几类：

一、当α>1时

特例：(1)画y=x2的图象(如图1)；(2)画y=x3的图象(如图2)；

(3)画y=x3/2的图象(如图3).

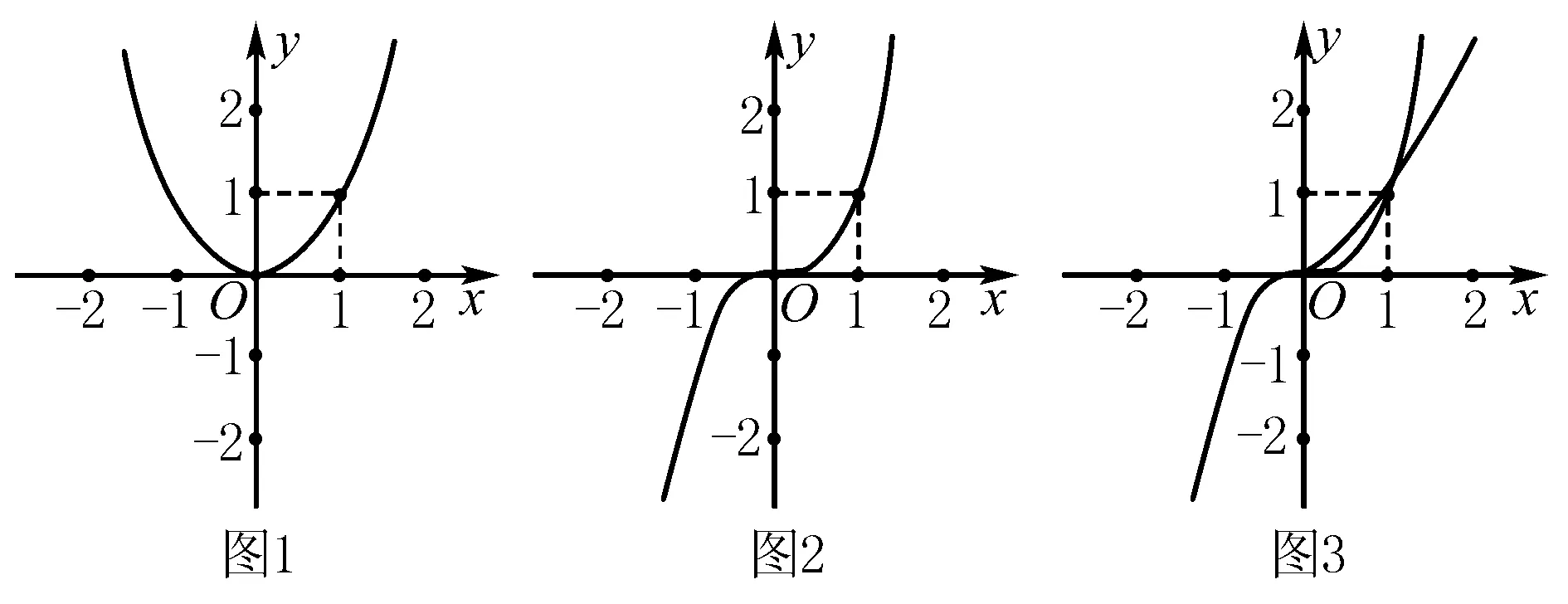
归纳 (1)当α=2,4,6,8,…，即α为大于1的偶数时.在第一象限内，图象经过点(0,0)和点(1,1)，且单调递增，图象为抛物线凹型；因为函数是偶函数，所以由偶函数图象关于y轴对称，即可画出其在第二象限内的图象(形状大致与图1相近).(2)当α=3,5,7,9,…，即α为大于1的奇数时.在第一象限内，图象经过点(0,0)和点(1,1)，且单调递增，图象为抛物线凹型；因为函数为奇函数，所以由奇函数图象关于原点对称，即可画出其在第三象限内的图象(形状大致与图2相近).(3)当α为大于1的分数，且分母是偶数、分子是奇数时.在第一象限内，图象经过点(0,0)和点(1,1)，且单调递增，图象为抛物线凹型；因为负数没有偶次方根，所以其函数只在第一象限内有图象(形状大致与图3相近).(4)当α为大于1的分数，且分母是奇数、分子是偶数(如y=x4/3)时，函数图象的形状大致与图1相近.(5)当α为大于1的分数，且分母与分子都是奇数(如y=x5/3)时，函数图象的形状大致与图2相近.

二、当0<α<1时

特例：(1)画y=x2/3的图象(如图4)；(2)画y=x1/3的图象(如图5).

(3)画y=x1/2的图象(如图6).

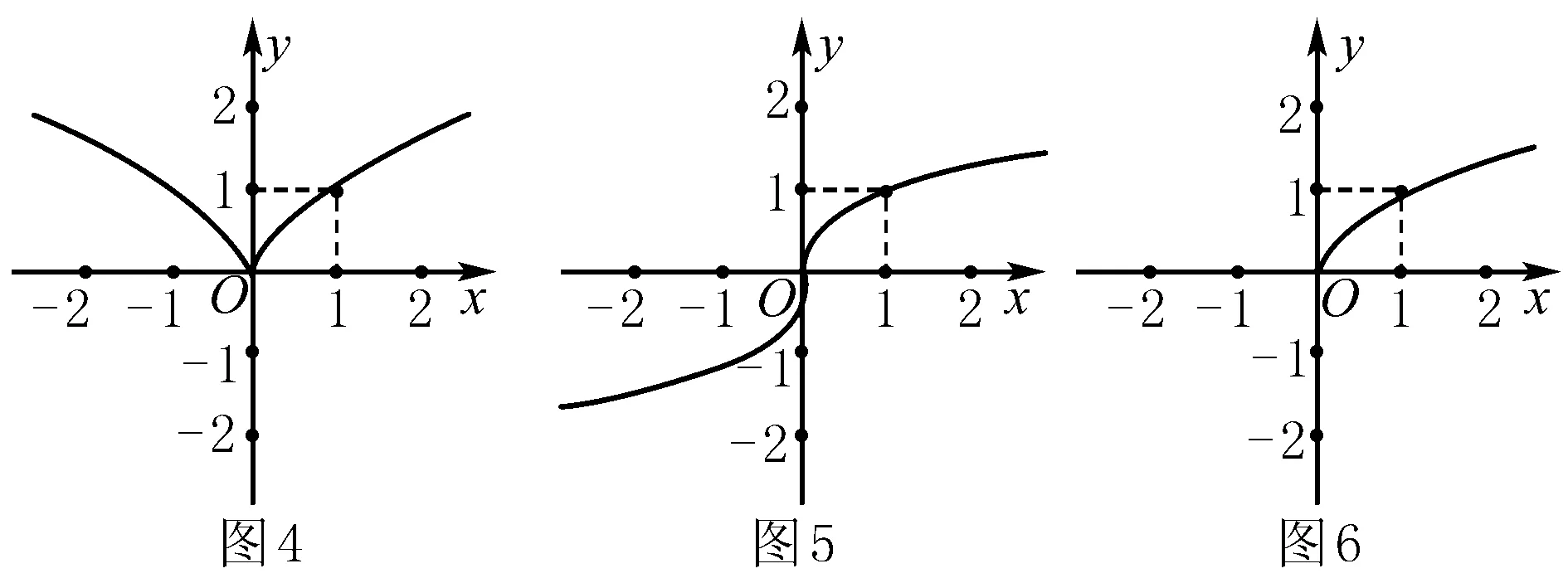
归纳 (1)当0<α<1的分数，且分母是奇数、分子是偶数时.在第一象限内，图象经过点(0,0)和点(1,1)，且单调递增，图象为抛物线凸型；因为函数是偶函数，所以由偶函数图象关于y轴对称，即可画出其在第二象限内的图象(形状大致与图4相近).

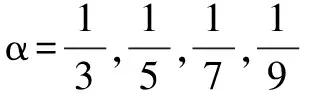
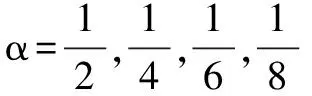
(4)当0<α<1的分数，且分子是奇数、分母是偶数(y=x3/4)时，函数图象的形状大致与图6相近.

(5)当0<α<1的分数，且分子与分母都是奇数(y=x3/5)时，函数图象的形状大致与图5相近.

三、当α<0时

特例：(1)画y=x-1的图象(如图7)；(2)画y=x-2的图象(如图8)；

(3)画y=x-3/2的图象(如图8).

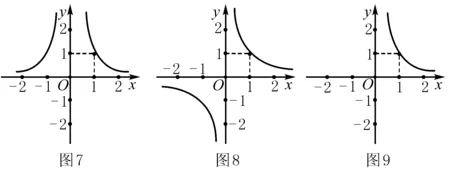
归纳 (1)当α=-2,-4,-6,-8,…，即a为小于0的偶数时.在第一象限内，图象经过点(1,1)，且单调递减，图象为双曲线型；因为函数是偶函数，所以由偶函数图象关于y轴对称，即可画出其在第二象限内图象(形状大致与图7相近).

(2)当α=-1,-3,-5,-7,-9,…，即a为小于0的奇数时.在第一象限内，图象经过点(1,1)，在区间(0,+)上单调递减，图象为双曲线型；因为函数是奇函数，所以由奇函数图象关于原点对称，即可画出其在第三象限内的图象(形状大致与图8相近).

(3)当α是负分数，且分子是奇数、分母是偶数时.在第一象限内，图象经过点(1,1)，且单调递减，图象为双曲线型.因为负数没有偶次方根，所以其函数只在第一象限内有图象(形状大致与图9相近).

(4)当α是负分数，且分子是偶数、分母是奇数(如y=x-2/3)时，函数图象的形状大致与图7相近.

(5)当α是负分数，且分子与分母都是奇数(如y=x-5/3)时，函数图象的形状大致与图8相近.

G632

B

1008-0333(2017)13-0028-02