等腰三角形中的数学思想大展播

江西省赣州市章贡区教师进修学校(341000)

吴宁娜●



等腰三角形中的数学思想大展播

江西省赣州市章贡区教师进修学校(341000)

吴宁娜●

本文例析了用不同数学思想解决等腰三角形的若干问题.

等腰三角形；讨论思想；方程思想；整体思想；由特殊到一般

一、讨论思想

例1 已知等腰三角形的一个角等于42°，则它的底角为( )．

A.42 ° B.69° C.69°或84° .D.42°或69°

分析 在等腰三角形中，当一个锐角在未指明为顶角还是顶角时，一定要分类讨论．

解 (1)当42°为等腰三角形底角的底角度数时，则顶角为180°-42°×2=96°，符合题意；

(2)当42°为等腰三角形的顶角度数时，则底角为(180°-42°)÷2=69°．

所以底角存在两种情况为42°或69°，选D．

例2 已知一个等腰三角形的一边上的高等于这边的一半，求顶角的度数．

分析 已知中的一边可能是底边，也可能是腰，所以需要分情况讨论．

解 (1)若这一边为底边时，如图1，AD⊥BC，AD=BD=CD，则△ABD和△ACD为等腰直角三角形，所以∠BAC=45°+45°=90°.

综上可知等腰三角形的顶角是90°或30°或150°．

评注 在解等腰三角形的问题时，若已知条件中边并没有指明是底还是腰时，应在符合三角形三边关系的前提条件下分类讨论.从而做到不漏解.

二、方程思想

例3 等腰三角形一腰上的中线把这个三角形的周长分成12cm和21cm两部分,求等腰三角形的底边长.

分析 这是几何中的代数问题,不妨考虑通过设未知数,利用方程(组)思想来解决.

解 设腰长为2xcm,底边长为ycm,则

答:这个等腰三角形底边长是5cm

评注 方程(组)思想是数学学习中的一个重要思想,它是通过设未知数,利用题意来设法建立方程(组),再求解,求出三角形的边必须用三角形边与边不等关系来检验,决定取舍.

三、整体思想

例4 如图4，在△BAC中，AB=AC,AB+BC=13,AB边的垂直平分线MN交AC于D,求△BCD的周长.

分析 要求△BCD的周长,只需求出BC+CD+BD即可,而MN垂直平分AB,可知BD=AD,从而将△BCD的周长转化为BC+AC,继而可使问题获解,又不必分别求出△BCD的三边长.

解 ∵MN垂直平分AB交AC于D,∴BD=AD.又∵AB=AC, ∴△BCD的周长=BC+CD+BD=BC+CD+AD=BC+AC=BC+AB=13.

评注 本题若分别求三边长,则不易求解,而巧妙地应用整体思想求解可使问题简单化.

四、由特殊到一般的思想

例5 (1)如图5，△ABC中，AB=AC，∠BAC=90°，则∠CBA与∠A的关系是____.

(2)如图6，△ABC中，AB=AC，∠A=50°,BD⊥AC于D，若∠CBD=33°，则∠CBD与∠BAC的关系是____.

(3)如图7，△ABC中，AB=AC，BD⊥AC交CA的延长线于D，若∠BAC=128°，则∠CBD与∠BAC的关系是____.

(2)∵AB=AC，∠A=50°，∴∠ABC=∠ACB=65°.

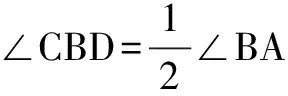
(3)∵AB=AC，∠BAC=128°，∴∠ABC=∠ACB=26°.

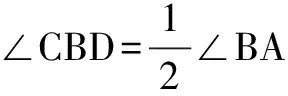
由(1)、(2)、(3)得出规律：等腰三角形一腰上的高与底边的夹角等于顶角的一半.

五、构造法

例6 如图所示，在△ABC中，AD⊥BC于点D，∠B=2∠C，求证：AB+BD=CD.

分析 由已知AD⊥BC，∠B=2∠C，如果我们在CD上截取DE=DB，连接AE，就可以构造出两个等腰三角形△ABE和△AEC.

证明 在上截取DE=DB，连接AE.∵AD⊥BC，DE=DB，∴AE=AB，∴∠B=∠AEB.又∵∠AEB=∠C+∠CAE=2∠C，∴∠CAE=∠C.∴AE=EC，AB+BD=AE+ED=EC+ED=CD.

G632

B

1008-0333(2017)14-0005-01