船舶可倾瓦推力轴承润滑油膜的轴向动特性计算方法

张赣波，赵 耀，储 炜，袁 华

（华中科技大学 船舶与海洋工程学院，武汉 430074）

船舶可倾瓦推力轴承润滑油膜的轴向动特性计算方法

张赣波，赵 耀，储 炜，袁 华

（华中科技大学 船舶与海洋工程学院，武汉 430074）

推力环和推力瓦之间的楔形润滑油膜是实现螺旋桨推力传递的重要环节，其轴向动特性直接关乎船舶轴系转子的纵向振动特性。文章分别论述了船舶可倾瓦推力轴承楔形润滑油膜轴向动特性的一维流近似解析方法和二维流数值方法，在已求得油膜静特性基础上，分别结合偏导数法和小摄动法获解了油膜动特性，推导了两种方法计算油膜动特性的求解式，并给出了详细计算过程。以某船舶可倾瓦推力轴承为算例，对两种方法的计算结果作了比较分析，得到了最小油膜厚度、油膜承载力和油膜轴向刚度三者间的一般变化规律，讨论了油膜动特性随轴转速的变化关系。计算结果为基于转子动态模型研究轴系纵向振动的传递机理提供了油膜动特性数据。

可倾瓦；推力轴承；动压润滑；油膜动特性

Key words:tilting pad;thrust bearing;hydrodynamic lubrication;oil film dynamic characteristics

0 引 言

实船上，米歇尔式（Michell）和金斯伯雷式（Kingsbury）两种类型的可倾瓦滑动式推力轴承由于具有结构紧凑、体积小、重量轻、摩擦系数小以及承载力大等优点获得了广泛应用。两者的结构差异主要在于推力瓦的支撑结构形式，前者为单点球面支柱刚性支撑，后者为平衡块交错叠加刚性支撑[1-2]。推力轴承是船舶推进系统中的最重要传力元件，其运行的安全稳定性直接关系到船舶的航行性能，故推力轴承设计要求有高度的可靠性，除必须与螺旋桨特性相匹配外，还需对其润滑性能和动特性进行分析和准确预测[3]。

推力轴承还作为螺旋桨脉动推力诱导的主推进轴系纵向振动向船体传递的重要通道，其动力学参数与主推进轴系纵向振动特性密切相关[4]。从转子动力学角度看，推力环与推力瓦之间的楔形润滑油膜是轴系转子连接轴承基座不可或缺的环节，但限于油膜自身的复杂性，以往对其轴向动特性的定量研究工作涉及较少。国内多数学者在研究船舶主推进轴系纵向振动特性时并未将油膜动特性纳入轴系动力学模型中，关于润滑油膜对轴系纵向振动特性的影响也始终未形成定论[5]。润滑油膜作为推力轴承实现螺旋桨推力传递的重要组成部分，明确其动特性可完善对推力轴承的动力学建模。

Schwanecke[6]和Vassilopoulos[7]较早开展推力轴承润滑油膜轴向刚度和阻尼的理论计算，其理论基础是简化的无限宽轴承润滑理论，由于忽略油膜压力沿径向的二次分布，且未考虑油膜的热效应，其分析方法还有待继续深入。润滑油膜动特性取决于推力瓦几何结构参数、润滑油物性参数和轴转速等因素，并与这些因素是一种高度复杂的非线性关系，其求解过程较为繁复，需遵循先静态后动态的计算顺序[8-9]。

本文先简要介绍了油膜轴向刚度的一维流近似解析方法，将扇形推力瓦近似为无限宽矩形滑块，获得了油膜承载力的解析式，求偏导得到了油膜轴向刚度；再基于二维流动压润滑理论论述了较为准确的油膜动特性计算方法，推导了油膜轴向刚度和阻尼的求解式，运用中差分法对动压润滑偏微分方程进行了离散数值求解，给出了详细计算流程，讨论了润滑油膜动特性随轴转速的变化关系，为后续主推进轴系转子系统轴向振动的传递机理分析作铺垫。

1 一维流近似解析方法

图1 可倾瓦推力轴承结构示意图Fig.1 Schematic diagram of tilting pad thrust bearing

可倾瓦推力轴承内部结构示意图如图1所示，推力环前后各有一排推力瓦，分别用于承受螺旋桨正倒车推力。图中各符号意义为：O为推力瓦几何中心，ω为轴转动角速度，φ为推力瓦圆心角，ri、ro分别为推力瓦的内外半径，b=ro-ri为推力瓦径向宽度，rp、θp分别为推力瓦支撑中心Op的径向和周向坐标，h2，h1分别为进出油口边油膜平均厚度。考虑推力瓦沿推力环分布的圆周对称性，各推力瓦与推力环之间楔形间隙内的油膜具有完全相同的几何形状，故只需讨论一个楔形油膜的润滑特性，即可获得推力轴承润滑油膜的总特性。

早期限于求解技术的发展，润滑油膜动特性（主要为刚度）的计算多基于简化的一维流动压润滑理论。一维流理论将实际扇形推力瓦近似简化为平面矩形滑块，只考虑油膜压力沿周向的二次分布，实际上相当于径向无限宽推力瓦，这样可将二维雷诺方程降阶为一维雷诺方程。平面矩形滑块油膜承载力的求解式为[10]：

式中：μ为轴承热平衡后的润滑油动力粘度；l=（ri+ro）φ/2为推力瓦平均半径处的周向长度；v=（ri+ro）ω/ 2为推力瓦平均半径处的线速度；a=h2/h1为推力瓦倾斜度。

由力矩平衡条件，可推导出推力瓦倾斜度a和推力瓦支撑中心与进油口边的距离L的关系式为：

船舶可倾瓦推力轴承推力瓦周向偏心距e的取值一般在0.05～0.1l范围内[11]，通常取为e=0.08l，则L=0.58l，代入（2）式可倒推出推力瓦倾斜度a。结合油膜承载力与螺旋桨静推力平衡条件，将已求解的推力瓦倾斜度a代入（1）式可计算出油口边油膜厚度h1。由此可见，一旦推力瓦支撑中心取定后，随着螺旋桨推力的变化，油膜厚度h1和推力瓦倾斜度a会自行调整。这正是可倾瓦推力轴承的结构特点。由于（2）式是超越方程，无法得到推力瓦倾斜度a的解析解，可通过一组a和L的离散值由Lagrange插值公式间接获解。a和L的对应值列于表1，当取L=0.58l时，插值可得推力瓦倾斜度a= 2.247 8。

为确定热平衡后的润滑油动力粘度，还需求解润滑油膜摩擦力和流量，两者求解式分别为[10]：

由绝热流动热平衡方程可得润滑油温升为：

式中：c、ρ分别为润滑油比热容和密度。

设润滑油进油口边温度为t0，则热平衡后的润滑油平均温度为：

式中：α为考虑实际轴承传导散热的影响予以修正的系数。船舶推力轴承属于中低速轴承，可取α= 0.8。

获解润滑油热平衡温度后，可由粘温关系获得对应温度的润滑油动力粘度。这里借用美国材料试验协会（ASTM）推荐的粘温指数公式：

式中：系数A和B可由润滑油两个已知温度下的粘度值确定。

将油膜承载力对油膜厚度求偏导，并考虑推力瓦支撑偏心的影响，得到油膜轴向刚度为：

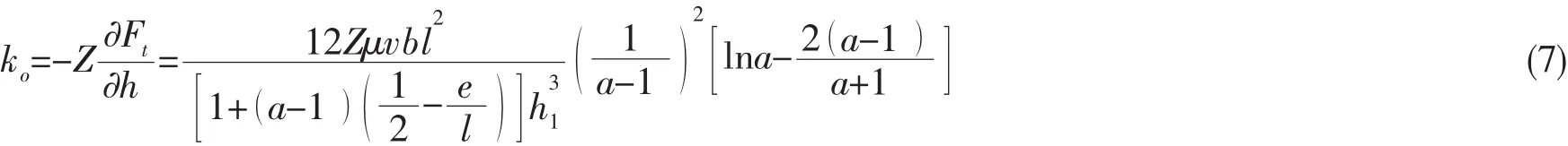
式中：Z为推力瓦数，μ和h1可结合（1）～（6）式获解。

一维流理论未考虑油膜压力沿径向的变化，计算油膜压力呈半圆柱面分布，在同样油膜厚度情形下，一维流计算油膜承载力必定大于实际轴承外荷载。当推力瓦宽长比满足b/l＞3时，一维流计算油膜承载力同实际值较为接近[12]，而实际船舶可倾瓦推力轴承推力瓦的宽长比一般为0.8～1，故按（7）式计算润滑油膜轴向刚度只能是近似的。

2 二维流数值方法

鉴于一维流理论的不足，且无法获解油膜阻尼，还需借助于二维流动压润滑理论，以实际有限宽扇形推力瓦为润滑油膜载体。

2.1 润滑油膜控制方程

（1）雷诺方程

雷诺方程可看作Navier-Stokes方程的特殊形式。对于可倾瓦推力轴承，建立如下柱坐标形式的稳态雷诺方程[10]：

（2）能量方程

润滑油粘性使其在运动过程中摩擦生热，导致进入楔形间隙内的油膜温度升高。流体动压润滑以对流散热为主要热传导形式，可近似为绝热流动，即摩擦热能全部由润滑油流动带走。由功、能守恒原理可推导出润滑油膜的绝热流动能量方程为[10]：

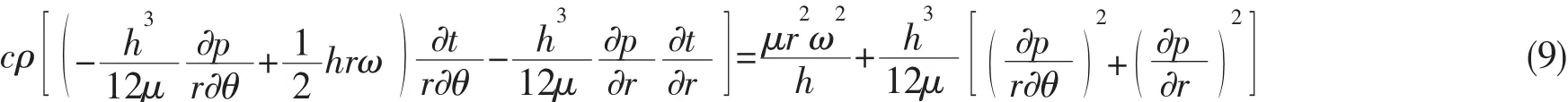
（3）膜厚方程

轴系稳定旋转过程中，推力瓦绕支撑点发生微小倾斜，可近似为线支撑，如图2所示。

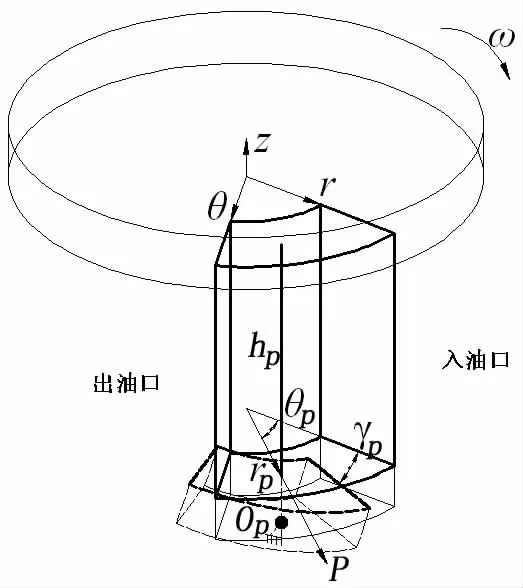
图2 推力瓦倾斜示意图Fig.2 Tilting sketch of pad

由几何关系可推导出油膜厚度方程为：

式中：hp为推力瓦支撑中心位置对应的油膜厚度，γp为推力瓦绕支撑线OP的倾斜角。一般地，γp很小，有tanγp≈γp。

设最小油膜厚度位置坐标为 （rm，θm），代入（10）式可得最小油膜厚度为：

对（11）式移项整理，代入（10）式，可得用最小油膜厚度表示的油膜厚度方程为：

雷诺方程和能量方程都是偏微分方程，且两者相互耦合，难以获得解析解，只能借助于数值计算方法。为改善数值计算的稳定性，并使分析结果具有普遍性，有必要对上述控制方程进行无量纲化处理。定义如下无量纲量：

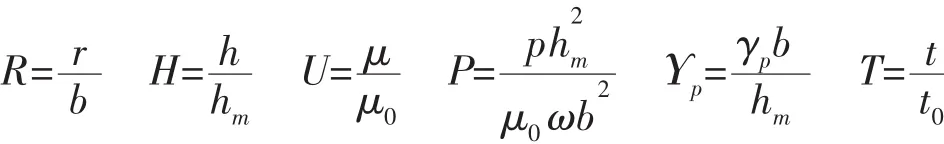
式中：μ0为对应进油口边温度t0的润滑油动力粘度。

结合上述无量纲量，直接推导出润滑油膜无量纲控制方程分别为：

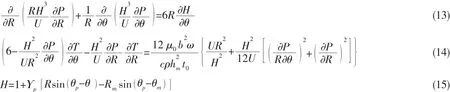
润滑油膜静特性包括油膜承载力和力矩等，其中，油膜力矩是油膜分布压力对推力瓦支撑中心的合力矩。两者将作为油膜压力场数值计算的控制条件，表达式分别为：

2.2 边界条件和控制条件

润滑油膜的边界条件包括压力、温度和粘度。其中，压力边界条件针对推力瓦四周边，温度和粘度边界条件只针对进油口边。四周边压力边界条件为：

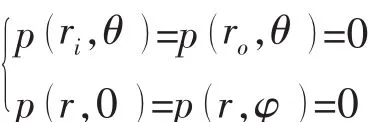
进油口边温度和粘度边界条件为：

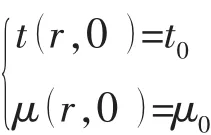
润滑油膜的控制条件是油膜承载力等于螺旋桨静推力以及油膜力矩等于零，即：

式中：KT为推力系数，一般由螺旋桨敞水性能试验获得，ρw为水密度，n为螺旋桨转速，D为螺旋桨直径。

2.3 数值计算

以单个推力瓦与推力环之间的润滑油膜为求解域，将润滑油膜划分为有限网格，如图3所示。将油膜沿周向划分为m格，分别编号1，L，m+1，周向步长为Δθ=φ/m；沿径向划分为n格，分别编号1，L，n+ 1，径向步长为ΔR=1/n。

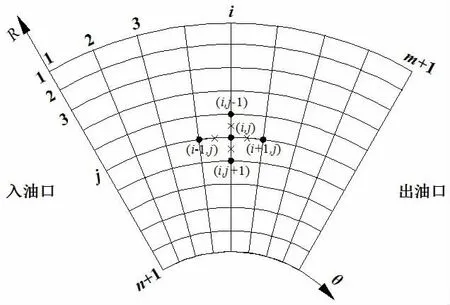
图3 润滑油膜有限差分网格Fig.3 Finite difference grid of oil film

这里直接给出无量纲雷诺方程和能量方程的中心差分格式：

式中：各系数分别为：

二维流变粘度润滑分析需联立求解雷诺方程、能量方程、粘温方程和膜厚方程，其数值计算流程为：首先以润滑油入口温度所确定的粘度值作为润滑油粘度的初值，求解雷诺方程获得等粘度条件下的油膜压力场，由所求油膜压力场求解能量方程获得油膜温度场，检查压力场和温度场是否满足给定收敛条件，若不满足，按粘温方程获解新的油膜粘度，再次计算雷诺方程和能量方程，直至压力场和温度场满足收敛条件；得到收敛的压力场后，继续检查是否满足控制条件，如满足，结束计算，否则修改相应变量，重新计算。数值计算流程框图如图4所示。内层迭代循环是油膜压力和温度，外层迭代循环是油膜承载力和力矩，修改变量是最小油膜厚度和推力瓦倾角。

编制计算程序时，为避免迭代发散或者陷入无限循环，必须采取一些措施[12]，如设置无量纲计算变量（P、T、H）的上下限(需根据实际推力轴承的润滑性能选取)；引入松弛因子，分别运用超松弛迭代法和低松弛迭代法计算油膜压力场和温度场；设置内外层循环的最大迭代次数等。

2.4 润滑油膜动特性

完成静平衡位置的油膜压力场和温度场的求解是分析油膜动特性的前提。油膜轴向动特性实际上反映油膜承载力的相应变化，故必须以非定常雷诺方程作为分析基础。在无量纲稳态雷诺方程中加入挤压油膜项，表达式为：

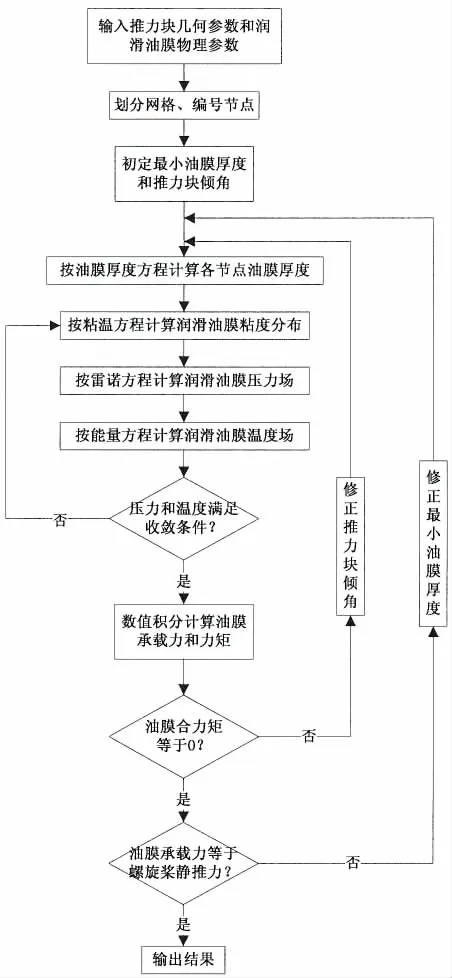
图4 二维流动压润滑数值计算流程框图Fig.4 Numerical calculation flow diagram of 2-D hydrodynamic lubrication

推力环在螺旋桨脉动推力作用下在其静平衡位置附近作微幅轴向振动挤压油膜，引起油膜厚度的扰动。油膜厚度可表示为：

式中：H0是静平衡位置油膜厚度，Xk和ξk分别是各简谐次轴向振动位移幅值和相位。

由（20）式可推导如下关系式成立：

油膜厚度的扰动引起油膜压力的扰动。小扰动条件下，油膜压力可近似表示为推力环偏离静平衡位置的轴向位移和速度的线性函数，此时用一个刚度和阻尼系数表示油膜的动特性。将油膜动压力在静平衡位置展开为轴向位移ΔH和速度Δ的一阶Taylor级数为：

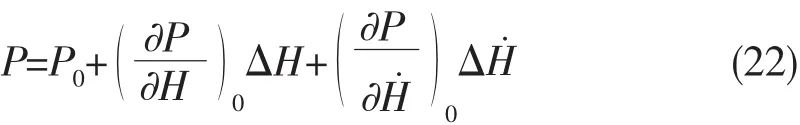
式中：P0是静平衡位置油膜压力分布值，下标0表示在静平衡位置取导数。

将油膜动压力沿推力瓦面积分求得油膜动承载力为：

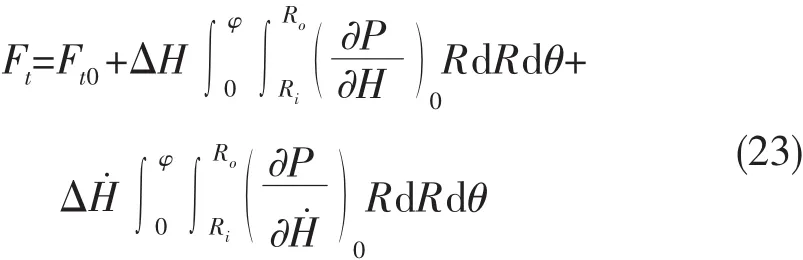
式中：Ft0是静平衡位置油膜承载力，对应于螺旋桨静推力。

由（23）式可直接得到油膜无量纲轴向刚度和阻尼求解式为：

由于无法得到油膜压力的显式表达式，由（24）式直接计算油膜动特性几乎不可能。为此，可将（20）式和（22）式代入（19）式，结合（21）式，比较方程两端对应项，同时略去高阶小量，整理得：

（25）式左端项与稳态雷诺方程式（13）形式完全相同，只是右端项稍有不同。可运用同计算雷诺方程的有限差分法对方程进行超松弛迭代求解得到，再代入（24）式，由Simpson数值积分法获得油膜的无量纲轴向刚度Ko和阻尼Co，量纲化后即可得实际润滑油膜的动特性。结合已定义的无量纲量，容易推得油膜量纲动特性与无量纲动特性的转化关系式为：

从（26）式看出，推力瓦径向宽度、油膜初始动力粘度、最小油膜厚度和轴转速是决定油膜动特性的关键因素。

3 算例分析

某可倾瓦动压润滑滑动推力轴承的推力瓦结构参数如表2所示。所用润滑油牌号为ISO VG46，密度为890 kg/m3，比热容为1 922.8 J/kg°C，在20°C和40°C时的运动粘度分别为105 mm2/s、46 mm2/ s，进油口温度为35°C，对应的动力粘度为0.051 Pa·s。

表2 推力瓦结构参数Tab.2 Parameters of pad

可倾瓦推力轴承的结构优势在于轴旋转过程中会自行形成一个收敛的楔形油膜和足够大的最小油膜厚度。由于螺旋桨推力是轴转速的函数，故不同轴转速对应的油膜动特性必然存在差异。表3列出典型转速下油膜轴向刚度的一维流和二维流计算结果。在分析过程中，螺旋桨静推力取为轴转速的二次方关系。比较看出，油膜轴向刚度一维流计算值均小于二维流计算值，分析有两方面原因：二维流考虑润滑油膜的径向端泄，计算油膜压力呈抛物面分布，与实际油膜压力场较为接近，在相同螺旋桨推力作用下，二维流油膜厚度必定小于一维流；一维流计算油流量偏小，油膜温升大，润滑油粘度降低。润滑油膜一维流模型相对二维流模型较为粗糙，但计算量显著减小。从算例结果看，油膜轴向刚度二维流计算值约为一维流计算值的2倍，但更准确的一维流模型修正值还需要更多算例分析予以获得。

图5给出二维流变粘度计算的油膜轴向刚度和阻尼随轴转速的变化关系。从图5看出，油膜无量纲轴向刚度和阻尼都在一个平均值附近波动，且波动幅值很微小，表明油膜无量纲特性受轴转速影响较小，这一规律有助于对油膜动特性的预估.实际油膜轴向刚度和阻尼都随轴转速增加递增，且两者数值均较大。对于独立安装的船用推力轴承，其纵向刚度范围为1×109～5×109N/m，比较可知，在轴中高转速行程内，油膜轴向刚度已超过推力轴承金属实体刚度。

表3 油膜刚度一维流和二维流计算值比较Tab.3 Comparison of oil film stiffness with 1-D and 2-D

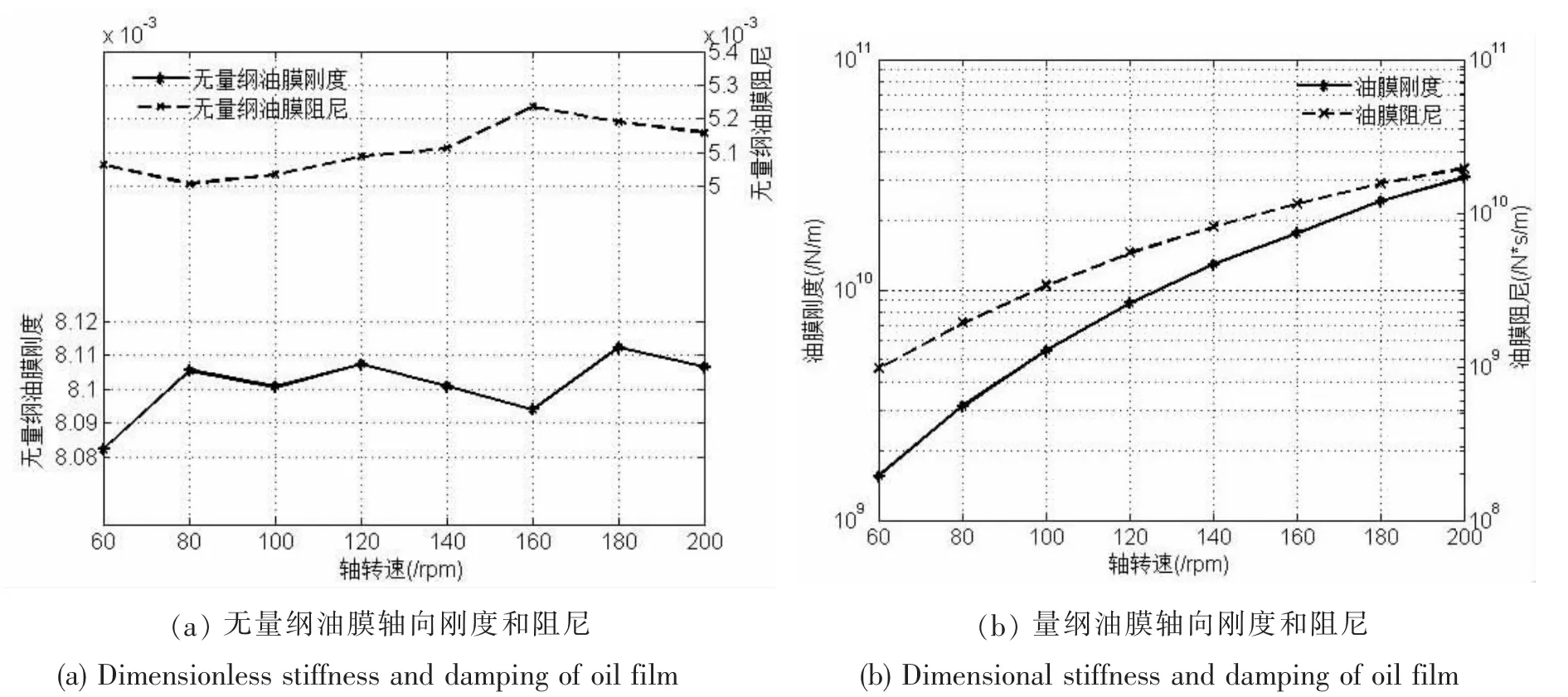
图5 油膜轴向刚度和阻尼随轴转速的变化关系Fig.5 Oil film stiffness and damping versus shafting rotating speed

油膜承载力决定于最小油膜厚度，而油膜轴向刚度又与最小油膜厚度相关，三者间的相互关系可用如图6所示的推力轴承动压特性曲线表示。从图6可见，最小油膜厚度与油膜承载力和油膜刚度呈负增长关系。随轴转速增加，油膜厚度迅速减薄，相应的油膜承载力和刚度迅速增加以适应增大的螺旋桨推力。

图6 推力轴承动压特性曲线Fig.6 Dynamic characteristic curve of thrust bearing

4 结 论

本文探讨了可倾瓦推力轴承楔形润滑油膜的轴向动特性，详细给出了两种方法的计算流程，结合某型推力轴承算例，得出了以下一些结论：

（1）油膜动特性分析需依据流体动压润滑理论，按对推力瓦模型的简化处理，分为一维流和二维流方法。一维流理论是近似方法，对油膜刚度的计算值相对偏低，二维流计算方法较为准确，但计算量显著增加；

（2）最小油膜厚度和轴转速是决定油膜动特性的最关键因素，油膜承载力和油膜轴向刚度与最小油膜厚度呈此消彼长关系；

（3）受螺旋桨脉动推力对润滑油膜的挤压效应，随轴转速增加，油膜轴向刚度和阻尼都逐渐增大，且两者量级均很高。在一定轴转速下，油膜刚度值超过推力轴承金属实体刚度。

[1]CB3103-81.船舶推进轴系滑动推力轴承[S].1982.

[2]胡荣华.船用滑动推力轴承结构设计研究[J].船舶工程,2007,29(5):60-64. Hu Ronghua.Structural design research of the marine thrust bearing[J].Marine Engineering,2007,29(5):60-64.

[3]Sternlicht D B,Reid J C,Arwas E B.Review of propeller shaft thrust bearings[J].A.S.N.E.Journal,1959,(5):277-289.

[4]张赣波,赵 耀.船舶主推进轴系纵向振动的弹性波解析研究[J].中国造船,2012,53(3):140-150. Zhang Ganbo,Zhao Yao.Elastic wave analysis on longitudinal vibration of marine propulsion shafting[J].Shipbuilding of China,2012,53(3):140-150.

[5]赵 耀,张赣波,李良伟.船舶推进轴系纵向振动及其控制技术研究进展[J].中国造船,2011,52(198):259-269. Zhao Yao,Zhang Ganbo,Li Liangwei.Review of advances on longitudinal vibration of ship propulsion shafting and its control technology[J].Shipbuilding of China,2011,52(198):259-269.

[6]Schwanecke H.Investigations on the hydrodynamic stiffness and damping of thrust bearing in ship[J].Transactions of the Institute of Marine Engineers,1979,(91):68-77.

[7]Vassilopoulos M L.Methods for computing stiffness and damping properties of main propulsion thrust bearing[J].International Shipbuilding Progress,1982,329(29):13-31.

[8]陈 渭.流体动压润滑推力轴承动特性及其对转子横向振动状态影响的研究[D].西安:西安交通大学,1991. Chen wei.The dynamic performances of hydrodynamic lubricated thrust bearing and the influence on crosswise vibration state of rotor[D].Xi’an:Xi’an Jiaotong University,1991.

[9]李 忠,袁小阳,朱 均.可倾瓦推力轴承的线性和非线性动特性研究[J].中国机械工程,2000,11(5):560-563. Li Zhong,Yuan Xiaoyang,Zhu Jun.A study of linear and non-linear dynamic performance for tilting-pad thrust bearing [J].China Mechanical Engineering,2000,11(5):560-563.

[10]温诗铸,黄 平.摩擦学原理[M].(第二版)北京:清华大学出版社,2002.

[11]商圣义.民用船舶动力装置[M].北京:人民交通出版社,1996.

[12]杨沛然.流体润滑数值分析[M].北京:国防工业出版社,1998.

Calculation method for axial dynamic characteristics of lubricant oil film in marine tilting pad thrust bearing

ZHANG Gan-bo,ZHAO Yao,CHU Wei,YUAN Hua
(School of Naval Architecture&Ocean Engineering,Huazhong University of Science&Technology,Wuhan 430074,China)

The oil film between thrust collar and tilting pads is one of significant transmitters for propeller thrust transmission.The axial dynamic characteristics of oil film make great influence on longitudinal vibration of propulsion shafting.In this paper,two methods are presented to evaluate the longitudinal stiffness and damping of oil film,namely one-dimension approximate analytical method and two-dimension numerical method.For the first method,the pad is interpreted as rectangle slider.While for the second method,the actual sector pad is directly used as objective.As the premise of dynamic analysis,the static characteristics of oil film with action of propeller steady thrust are firstly carried out based on dynamic lubrication principles.And then the calculations of oil film dynamic characteristics are derived in great detail by the partial derivative method and the small perturbation method.Taking the example of a marine thrust bearing, the comparison of results with two proposed methods is conducted.Further,the relationship among minimum film thickness,film carrying capacity and film stiffness is analyzed,and so also is for the rule between oil film dynamic characteristics and shafting rotating speed.The values of oil film dynamic characteristics can be applied for transmission research of propulsion shafting longitudinal vibration.

U664.3

：Adoi:10.3969/j.issn.1007-7294.2017.05.011

1007-7294（2017）05-0603-10

2016-12-07

教育部高等学校博士学科点专项科研基金项目（20130142110014）；国家自然科学基金委员会资助项目（51479078）

张赣波（1987-），男，博士研究生，E-mail：hustzgb@126.com；赵 耀（1958-），男，博士，教授，博士生导师，E-mail：yzhaozzz@hust.edu.cn。