优化学生CPFS结构的课堂小结研究——以“等差数列前n项和求最值”教学为例

何英

优化学生CPFS结构的课堂小结研究
——以“等差数列前n项和求最值”教学为例

何英

实际课堂中，各种各样的原因使得课堂小结往往形同虚设。其实课堂小结可以作为优化学生CPFS结构的重要环节。教师应将课堂小结这个环节交给学生，给学生留足时间自主建构概念域、命题域，从而达到完善CPFS结构的目的。

CPFS结构；课堂小结；自主建构

一堂好课，要有引人入胜的课题导入，扎实有效的课堂建构，画龙点睛的课堂小结。但实际课堂中，教师或因时间预设不充分，抽不出时间小结，或因课堂中每个节点都已经小结过，觉得没必要小结，课堂小结往往形同虚设，给教学留下了遗憾。其实，课堂小结可以作广义的理解，即师生在完成一项任务后对所学知识的归纳总结。在这里，课堂小结并非仅仅是知识与技能的简单回顾，我们可以利用课堂小结来完善学生的CPFS结构。

一、CPFS结构概述

南京师范大学喻平教授对学生的认知心理结构做了深入的研究，提出了CPFS结构这个观点。喻平教授将概念域 （concept field）、 概念系（concept system）、命题域（proposition field）、命题系（proposition system）形成的心理结构称为CPFS结构。

1.概念域与概念系。

概念C的所有等价定义的图式，叫作概念C的概念域。具体地说，概念域的含义是指某个概念的一些等价定义（知识）在个体头脑中形成的知识网络，是个体对数学知识的表征。

如果一组概念 C1，C2，…，Cn存在关系C1R1C2R2…Rn-1Cn（*），其中Ri（i=1，2，…，n）表示强抽象、弱抽象、广义抽象这3种数学关系中的任意一种，那么称*式为一条概念链，记为λ={C1，C2，…，Cn}。如果两条概念链的交集非空，则称这两条链相交。如果m条概念链中至少有一条与其余的链都相交，那么称这m条链的图式为概念系。

2.命题域与命题系。

命题域（系）是概念域（系）的自然推广。如果命题A成立，当且仅当命题B成立，那么就称A与B是等价命题，记为A⇔B。与命题A等价的所有命题组成的命题集叫作命题A的等价命题类，记为{A1}，并称A为典型命题。典型命题A的等价命题类{A1}连同这些命题之间的（互推）关系所形成的结构叫作等价命题网络。我们称一个等价命题网络的图式为典型命题A的命题域。

如果一组命题A1，A2，…，An存在推出关系（广义抽象）A1⇒A2⇒…⇒An，则称其为一条命题链，记为λ={A1，A2，…，An}。如果m条命题链中的每一条都至少与其余一条相交（交集非空），那么称这m条链组成的系统为半等价命题网络。一个半等价命题网络的图式称为命题系。命题系是命题域的推广，命题域往往作为某个命题系的子图式。

概括而言，CPFS结构的含义是：（1）个体头脑中内化的数学知识网络。各知识点（概念、命题）在这个网络中处于一定位置，知识点之间具有等值抽象（等价）关系，或强抽象关系，或弱抽象关系，或广义抽象关系。（2）由于网络中知识点之间具有某种抽象关系，而这些抽象关系本身就蕴涵着思维方法，因而网络中各知识点之间的连线包含着数学方法。（3）CPFS结构既包含了表征陈述性知识的图式，又包含表征程序性知识的产生式系统。

由上述内容，我们可知，CPFS结构包含了学生解题时需要动用的一切信息，所以若CPFS结构不完善，即使学生课上能听懂，但自己解题时仍旧会感觉困难。一方面可能因为题目已将命题或概念换了一个表述方法，而由于学生不完善的CPFS结构缺乏这个信息，所以连题目都无法读懂；另一方面，即使学生看懂题意，但在不完善的CPFS结构中调动不出相应环节的命题域或命题系，所以找不到解决问题的办法。

二、实施案例

CPFS结构是学生根据自己特有的感觉、知觉、记忆、思维、联想等对所学过的相关信息（概念、命题、思维方法）在头脑中存储的有规律的网络结构，其他人是看不见的，甚至学生自己在解决数学问题时也是无意识地在调动他的CPFS结构中的信息。要想检视学生的这个结构是否完善，首先需要将这种看不见的思维变成可视的形式，所以我们要借助一切有效的方式把学生的CPFS结构呈现出来，概念图就是一种有效的工具。

概念图是一种用节点代表概念、连线表示概念间关系的图示法，一般由“节点”“连线”和“有关文字标注”组成。节点是利用几何图形、图案、文字等表示某个概念，每个节点表示一个概念，一般同一层级的概念用同种的符号（图形）标识。连线表示不同节点间的有意义的关系，常用各种形式的线联结不同节点，这其中表达了构图者对概念的理解程度。文字标注可以表示不同节点上的概念的关系，也可以是对节点上的概念详细阐述，还可以是对整幅图进行有关说明。它是一种知识以及知识之间的关系的网络图形化表征，也是思维可视化的表征。将抽象的思维变成可视的、形象的图示，便于学生检查和修改CPFS结构中不完善的部分，也便于学生理解记忆。

下面借助一节关于等差数列的前n项和Sn求最值的新授课来进行说明。

1.教学过程。

（1）复习回顾等差数列前n项和公式的多种表达形式。

（2）典例呈现。

例1 已知an=4n-37，求使得Sn取最小值时的n的值。

方法1 学生把Sn求出来，从二次函数的角度求得了最值，教师提醒要注意定义域。

方法2 教师引导学生从等差数列单调性的特征出发，列出不等式组，求得了n的值。

变式1 等差数列{an}中，a4=36，d=-6，求Sn最大值。

变式2 已知{an}为等差数列，a1＞0，S4=S9，求n为何值时，Sn最大？使Sn＞0的最小正整数为多少？

变式3 已知{an}为等差数列，a1＞0，S9＞0，S10＜0，求n为何值时，Sn最大？

2.基于优化CPFS结构的课堂小结设计。

为了让学生完善CPFS结构，教师可以以问题为驱动，引导学生先建构各种概念（命题）系、概念（命题）域。

师：今天我们学习了如何求等差数列的前n项和的最值，追本溯源，请同学们思考以下问题：

问题1 为何等差数列的前n项和有最值？

学生在回答这个问题时就要建构以下概念域或概念系。

概念域：函数的最大（小）值即定义域中函数值的最大（小）值。

函数图像的最高（低）点的纵坐标即为该函数的最大（小）值。

概念链λ1={C1，C2，C3}，C1：函数的定义。C2：二次函数的定义。C3：公差不为0的等差数列前n项和Sn为定义域为正整数的二次函数。

由上述信息综合得等差数列的前 n项和是定义域为正整数的二次函数，所以一定有最值。

问题2 如何求等差数列的前n项和的最值？

问题3 等差数列的前n项和的先增后减（或先减后增）的特点本质上是由数列的什么性质决定的？

学生继续在头脑中提取相关信息，构建概念（命题）域：

{an}是等差数列，当且仅当an+1-an=d，d为常数，n∈N*⇔

{an}是等差数列，当且仅当 an+1-an=an-an-1，n≥2，n∈N*⇔

{an}是等差数列，当且仅当an+1=a1+（n-1）d，n≥2，n∈N*⇔

{an}是等差数列，当且仅当 an=am+（n-m）d，d为常数，n，m∈N*⇔

{an}是等差数列，当且仅当an=dn+（a1-d），d为常数，n∈N*。

概念链λ2={C1，C4，C5}

C1：函数的定义；C4：一次函数的定义；C5：公差不为0的等差数列通项公式an为定义域为正整数的一次函数。

概念链λ3={C6，C7，C8，C9}

C6：函数的性质。C7：函数的单调性。C8：一次函数的单调性。C9：等差数列的通项公式的单调性。

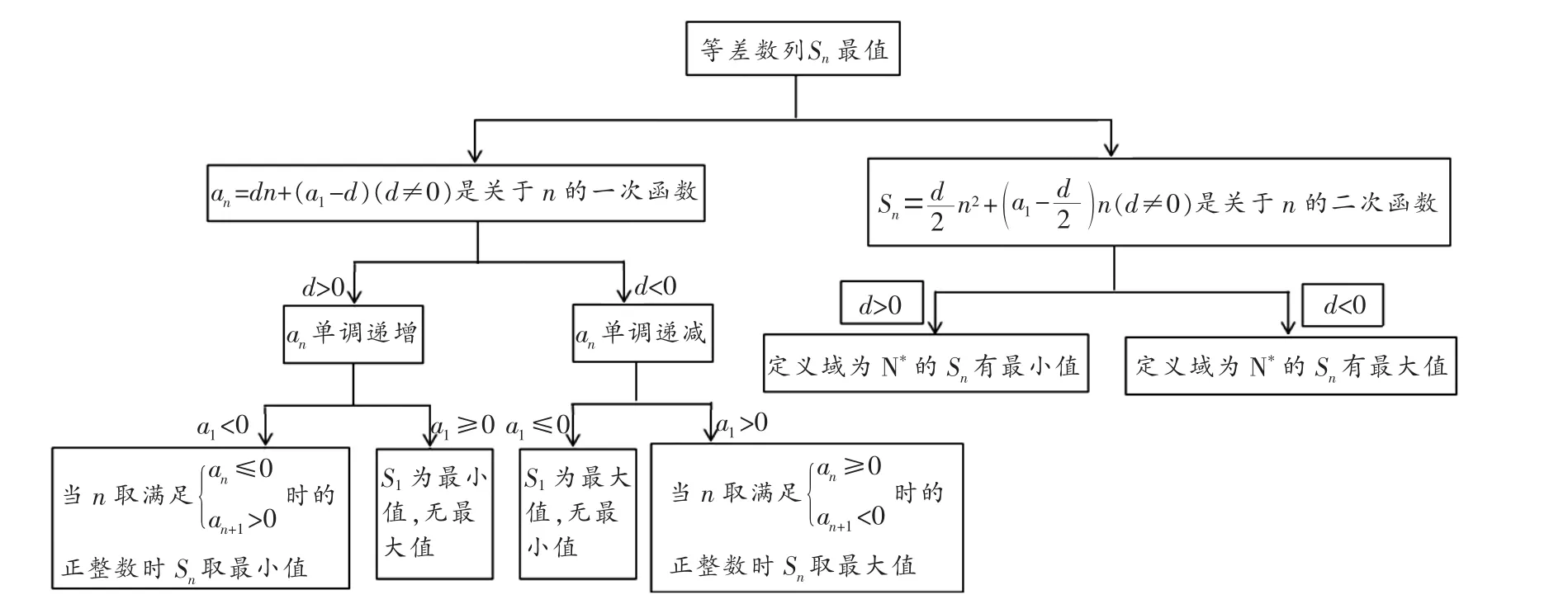
图1

综合这些信息，学生得到等差数列通项的相关性质：d≠0时，an是关于n的一次函数，若d＞0，则an单调递增，若d＜0，则an单调递减；若等差数列的首项为负数，公差为正数，则该数列中的项会由负数递增为正数，当前n项和再加上一个负数项时，和变小，加上一个正数项时，和变大，所以前n项和先减后增，加上最后一个非正数的项后即求得和的最小值；反之，若等差数列的首项为正数，公差为负数，则等差数列的前n项和先增后减，加上最后一个非负数的项后即求得和的最大值。所以，若a1＜0，d＞0，则由求使Sn取最小值的n；若a1＞0，d＜0，则由求使Sn取最大值的n。

上述信息可用概念图表示，如文末图1。

若学生能亲历小结的过程，必将在头脑中搜索到上述相关概念系及命题系。若学生能自主归纳出两种解法的原理及方法，必能更灵活地运用它们解决相关问题，如变式2，3。

课堂小结对学生的语言组织能力、概括抽象能力、知识的理解程度有很高的要求，所以初始尝试时教师须给予学生悉心的指导、耐心的帮助以及热情的鼓励，教师若能长期坚持，学生的学习定会达到事半功倍的效果。

［1］喻平，单墫．数学学习心理的CPFS结构理论［J］．数学教育学报，2003（01）.

［2］喻平.数学教学心理学［M］.北京：北京师范大学出版社，2010.

［3］曹才翰，章建跃．数学教育心理学［M］．北京：北京师范大学出版社，1999．

G633.6

A

1005-6009（2017）27-0043-03

何英，江苏省太湖高级中学（江苏无锡，214125）教师，一级教师。