“除数是小数的除法”教学研究报告

一、问题

小数除法计算是人教版数学教材五年级上册中的一个内容，这个内容分两个部分：除数是整数的除法和除数是小数的除法。除数是小数的除法是本单元的学习重点，其关键是把除数是小数的除法转化成除数是整数的除法。学生由于在这之前计算的都是除数是整数的除法以及受其他一些因素的影响，在计算除数是小数的除法时，尽管老师反复讲解，也多次进行练习，还是经常出错。一线数学教师普遍反映这个内容难教、学生难学。我校数学组在这个内容的教学上进行了尝试与思考，力图在计算正确率上有所突破。

1.教学实践中的问题及原因分析

为了更加清楚地掌握学生出错的原因，我们对学过的50名学生做了一个调查。题目如图1所示。通过调查，我们发现学生主要存在以下五個问题。

（1）学生计算时把除数当作整数，而被除数则不变（如图2所示）。

学生以前学习的都是除数是整数的除法，受定式思维的影响，在遇到除数是小数的除法时，习惯将它按照除数是整数的除法进行计算。之所以会出现这样的错误，是学生没有进一步思考：除数扩大变成整数后，如果被除数不跟着扩大相同的倍数，商的大小就改变了。

（2）学生不知道怎样转化。

学生计算5.88÷0.56时，会把被除数、除数同时扩大100倍，变成588÷56，而在计算0.544÷0.16时，却把被除数0.544扩大1000倍变成544，除数0.16扩大100倍变成16。可以看出，学生知道计算时要把除数转化为整数，但没有根据商不变的性质把被除数和除数同时扩大相同的倍数。

（3）学生忘记打小数点（如图3所示）。

（4）当被除数不够除时，学生没有在商中间相应的位置添0占位（如图4所示）。

（5）学生试商不熟练。

进一步分析这5种错误，我们发现：第1、2种错误的原因是学生没有掌握知识的关键点———怎样将除数是小数转化成除数是整数；第3、4、5种错误的原因是学生对以前所学的与此知识相关的基础知识掌握得不牢固。

2.教学对策

通过对学生出错原因的分析，我们认为在教学这个内容时，应将重点放在帮助学生解决如何将除数是小数转化成除数是整数上。

（1）引导学生自主分析出错的原因。

由于除数是小数的除法是在除数是整数的除法基础上进行学习的，在教学除数是小数的除法时，教师一般会让学生先尝试做一做。一些基础知识掌握得不扎实的学生难免会出错。教师可以趁机引导学生分析错误的原因，让他们知道自己错在哪里，应该怎样改正。比如，有学生在尝试计算7.65÷0.85时出错了，在汇报时，教师除了讲解如何正确计算外，还应该跟其他学生一起，倾听出错的学生是怎样想的，帮助他分析原因，纠正错误，避免下次再错。

（2）针对知识的关键点进行转化的专项练习。

除数是小数的除法是老师们公认的计算教学中的一大难点。为什么学生老是出错呢？通过测试、分析、研讨，我们发现：其实除数是小数的除法与除数是整数的除法在计算方法上是一致的，关键是学生需要根据商不变的性质把除数由小数转化成整数再进行计算。学生容易出错是因为不会进行转化。再反观我们的课堂，教师在课堂上很少甚至是没有针对除数和被除数小数位数的不同情况，让学生进行专门的转化练习，没有很好地突破难点，学生出错也就在所难免。基于此，我们觉得在探究新知环节后要针对这个关键点，专门设计转化的练习。如，先出示一组包含各种情况的除数是小数的计算题，要求：不计算，直接把它们转化成除数是整数的除法。接着引导学生观察转化后的除数，发现扩大10倍、100倍、1000倍，就是把小数点向右移动一位、两位、三位。紧跟着出示一组包含各种情况的除数是小数的计算题，要求学生直接移动小数点，把它们转化成除数是整数的除法算式。这样放慢节奏、放缓坡度，把重点放在把除数由小数转化成整数上。

二、实践

1.帮助学生辨析计算错误的原因。

师：现在，你想挑战一下，计算出7.65÷0.85的得数吗？给你4分钟时间，开始。

师巡视，指名做完的学生板演（如图5所示）。

师：算出的结果等于9，你是怎样算出来的？

生1：把除数的小数点向右移动2位，化成整数，然后把被除数的小数点也向右移动2位。这样都变成整数，就是整数除以整数啦。

师：我们一起看看他是怎样变成整数除法的（边说边用手指竖式）。除数0.85变成85，扩大100倍。被除数7.65变成765，扩大100倍。也就是除数和被除数同时扩大100倍，商不变，这是我们学过的商不变性质。有个同学是这样算的（如图6所示），你们觉得他这样做是怎样想的？

生2：他是把0.85扩大100倍，而7.65不变，商就是原来的百分之一。

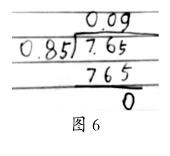
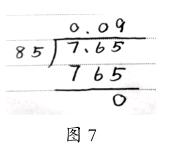
师：他的意思是：被除数没变，还是7.65，除数变成85。（在旁边板书竖式，如图7所示）原来7.65÷85的结果才是0.09，出现这个结果是他把除数当作85计算的。如果除数扩大100倍，但被除数不变，商就是原来的百分之一，如果还原就要扩大100倍。7.65÷0.85正确的结果是9。现在我们回过头看看：7.65÷0.85，除数是小数的除法我们是怎样算出结果的？

生3：把它转化成除数是整数的除法。

生4：把除数和被除数同时扩大相同的倍数再计算。

师追问：扩大相同倍数的目的是什么？

生5：使除数变成整数，商的大小也不变，就是我们学过的知识了。

设计意图：设计辨析错误的环节，帮助学生分析并弄清错误的原因，加深印象，避免再出错。

2.专门设计转化的环节，帮助学生突破难点。

师：把下面的算式转化成除数是整数的除法算式。说说你是怎样将除数转化成整数的。

2.38÷0.340.544÷0.165.2÷0.32

生6：2.38÷0.34，先把被除数2.38扩大100倍，变成238；（生说，师画箭头）再把除数0.34扩大100倍，变成34。（师完善板书）

师总结：把被除数2.38扩大100倍，变成238；再把除数0.34扩大100倍，变成34。那0.544÷0.16呢？

生7：先把0.544乘1000，变成544；再把0.16乘1000，变成160。（板书）

师：你这样做的依据是什么？

生7：因为0.544已经乘了1000，要使商不变，0.16也要乘1000。

师：也就是要同时乘1000。现在变成了544÷160。还有同学举手，你来说。

生8：把0.544乘100，变成54.4；然后0.16也乘100，变成16。这样就变成了学过的除数是整数的除法。

师：看来乘100也可以啊。既然乘100就可以了，何必乘1000呢？只要把除数变成整数就可以了，被除数是不是整数我们都会计算了。所以计算除数是小数的除法时，我们一般是以除数为准，先把除数变成整数，再将被除数扩大相同的倍数，然后进行计算。

设计意图：利用把0.544÷0.16转化成除数是整数这一题，引导学生思考、比较，让学生体会把它转化成54.4÷16比转化成544÷160要更合理、简洁，进而发现计算小数除法时，是根据除数的小数位数进行转化。

师：接下来我们看5.2÷0.32。谁来说说你是怎么计算的？

生9：把除数0.32扩大100倍变成32，再把被除数5.2扩大100倍，变成520。

师追问：为什么扩大100倍？

生9：这样的话除数就变成整数了。

师：我们把这3个算式转化成了除数是整数的除法，仔细观察，我们是怎样把它们转化成除数是整数的除法的？

生10：将被除数与除数同时扩大100倍。

师：都是扩大100倍，那小数点如何移动呢？

生11：向右移动2位。

师：扩大100倍，其实就是把小数点向右移动2位。下次扩大100倍时，就不用乘100，直接把小数点向右移动2位。扩大10倍时，就直接把小数点向右移动1位；扩大1000倍时，就直接把小数点向右移动3位。现在，我们可以直接移动小数点的位置，把除数是小数的除法转化成除数是整数的除法。请大家直接移动小数点的位置，把这些算式转化成除数是整数的除法。

5.58÷3.17.05÷0.470.756÷0.18

51.3÷0.2725.6÷0.3226÷0.13

生12：5.58÷3.1，把3.1的小数点向右移动1位，把5.58的小数点也向右移动1位，变成55.8÷31。（生说，师移动小数点）

师：现在请在练习纸上将剩下的几题移动小数点的位置，把它们转化成除数是整数的除法。2分钟时间，看谁做得又快又对。

学生动手练习。

师：老师走了一圈，发现大家做得很好，我们重点看看第二排的几道题。51.3÷0.27，谁来说说你是怎么做的？

生13：将0.27的小数点向右移动2位，51.3的小数点向右移动2位，变成5130÷27。

师追问：51.3怎样移动小数点变成5130？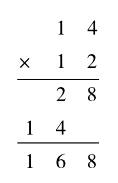

生13：将51.3的小数点向右移动1位，变成513；再向右移动1位，添0，变成5130。（生说，师用手势展示移动的过程）

师：那26÷0.13呢？

生14：先把除数0.13的小数点向右移动2位，再把被除数26的小数点也向右移动2位，添1个0，再添1个0。（生说，师用手势展示移动的过程）

师：被除数位数不够就在末尾补0，26÷0.13就变成了2600÷13。

设计意图：针对小数除法计算过程中最关键的步骤精心设计，旨在分散知识的难点，提高学生计算的正确率。

三、思考

1.课前巩固整数除法的计算，为除数是小数的除法扫清障碍。

回顾学生学习除数是小数的除法的过程，我们发现很多学生由于对除数是整数的除法计算不熟练，导致在除数是小数的除法计算中出现各种错误，如：计算时商的中间有0，没有在商的相应位置添0占位；试商不熟练，等等。同时，老师们发现小数除法之所以难教、难学，一个重要原因是，即便学生正确地将小数除法转化成整数除法后，很多学生还是不会做。而出现这种情况是因为学生在计算除数是两位数的除法时不会试商。因此，计算教学中，在开展新内容的教学之前，根据需要可以增加一节预备课，用于复习、巩固新知识学习的必备基础。比如，学习除数是小数的除法之前，花一节课时间复习除数是两位数的整数除法；学习除数是两位数的除法之前，花一节课时间复习除数是一位数的除法；学习两位数乘三位数的乘法之前，花一节课时间复习一位数乘多位数的乘法。所谓“磨刀不误砍柴工”。我校数学组一直坚持每天做“计算三分钟”练习，五年级学生在学习除数是小数的除法之前就可以利用这个计算練习时间有针对性地练习整数除法中学生的知识薄弱处和容易出错的地方，为除数是小数的除法学习扫清障碍。

2.暂时讲不清道理时不妨直接告诉学生。

在数学课堂上，我们经常会碰到这样一种情况：有的知识点试图和学生说道理时，发现目前难以找到简单有效的方法让学生明白。如果继续说下去，不仅耽误了课堂宝贵的时间，效果还不好。这时老师该如何取舍呢？我们是否可以换种思路，当道理说不清楚时不妨直接告诉学生呢？本节课学习的除数是小数的除法，在计算时要将算式转化成除数是整数的除法，为什么是以除法为准而不是以被除数为准呢？处理这个问题时，我们发现很难找到一个突破口，也无法跟学生说清楚。再三思考后教师做了这样的处理：没有在计算7.65÷0.85时就直接告诉学生把它转化成刚学过的除数是整数的除法来计算，而是放在练习环节进行处理。在将0.544÷0.16转化成除数是整数的除法算式时，学生出现了两种答案544÷160和54.4÷16，教师顺势引导学生对两种答案进行对比，从而发现：其实转化成54.4÷16我们就会计算了。这时教师告诉学生在计算除数是小数的除法时，只要把除数变成整数就可以了，被除数是不是整数我们都会计算了。因此在计算除数是小数的除法时，我们一般是以除数为准，先把除数化为整数，再将被除数扩大相同的倍数。

在计算教学中，与这种情况类似的还有三年级下册两位数乘两位数这一内容。以14×12为例，用竖式计算如右图所示。竖式这样写时，我们一般先用第二个因数12中个位上的2乘14，再用十位上的1乘14。为什么不先用第一个因数14中个位上的4乘12，再用十位上的1乘12呢？虽然我们都是把其中一个因数拆成几十加几，再分别用个位上的几乘另一个因数和十位上的几乘另一个因数，但用竖式计算时我们一般就是把第二个因数拆成几十加几再计算，而不拆第一个因数。教学时也很难和学生说清楚道理，我们同样也可以选择直接告诉学生。

计算能力对学生而言是很重要的一项技能，能为学生以后的学习提供必要的基础。在日常教学中，我们老师一定要持之以恒，想方设法提高学生的计算能力，从而让计算教学更高效。

（执笔：姚鑫、陈艳萍、谢凌燕、陈安、贺迎舟、郑志刚、徐旺、李闯）