基于非线性效用函数的多属性模糊决策分类算法

蒋莹莹，王惠文（云南师范大学 数学学院，云南 昆明 650500）

基于非线性效用函数的多属性模糊决策分类算法

蒋莹莹，王惠文
（云南师范大学 数学学院，云南 昆明 650500）

模糊环境下，基于非线性效用函数和级别优于关系的分类算法提供一个好的分类决策方法.此方法利用模糊理论及模糊数排序准则将含有三角模糊数的决策模型转换成普通决策模型，再采用加权求解的方法将多目标规划转换成单一目标规划.通过数值实例验证算法的有效性.

非线性效用函数；模糊理论；三角模糊数；加权

0 引言

多属性决策问题是在考虑多个属性状态下，选出最优的方案或对方案进行排序的分类决策问题.普遍存在于经济、社会生活的方方面面.由于人类思维的模糊性和客观事物的复杂性，客观实际中存在众多的模糊性事件和现象，促使人们寻求建立一种适于描述模糊事物和现象的逻辑模式.美国控制论专家Zadeh［1］教授清楚地认识到数学为什么会与人脑思维相分离和从什么地方开始分离的本质之后，重新把模糊性和数学统一在一起.1965年Zadeh教授第一次提出模糊集［2］的概念，用隶属函数［2］来刻画元素对集合属于程度的连续过度性.模糊集合理论自诞生以来研究的范围变得广阔，从开始的模糊集合，发展为模糊数、模糊代数、模糊积分、模糊规划、模糊图论等众多的分支，扩展数学研究的层面.同时效用理论［2-3］作为评价与度量的基础渐渐被社会大众接受.大部分的决策亦是借助于效用函数［3］来对方案进行选优和分类.总结闫艳［4］、郭嗣宗［5］等人研究的模糊数排序方法，提出新的模糊数排序准则转换决策模型进行决策.

1 预备知识

1.1 偏好于效用函数

定义1［3］严格序“≻”：a≻b（或记作aPb）的含义是“a优于b”；若非外界因素的强迫，决策人只会选择a而不会选择b.

定义2［3］无差异“～”：a～b（或记作aIb）的含义是“a无差异于b”；决策人对选择a或b同样满意.

定义3［3］弱序“”：ab（或记作aRb）的含义是“a不劣于b”，即a优于或无差异于b.

定义4［3］在集合P上的实值函数u，若它和P上的优先关系一致，即若P1,P2∈P,P1P2当且仅当则称u为效用函数.

1.2 隶属度

定义5 论域X到［0，1］闭区间上的任意映射都确定X上的一个模糊集͂，μA͂叫做͂的隶属函数［2］，叫做x对͂的隶属度，记为显然，模糊͂完全由隶属函数刻画，当时，A͂退化为A退化为特征函数CA(x).

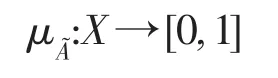
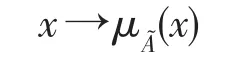
1.3 三角模糊数

用有序三元组数表示，其中分别表示͂的下限和上限，n为͂的中间值.其隶属程度定义如下：

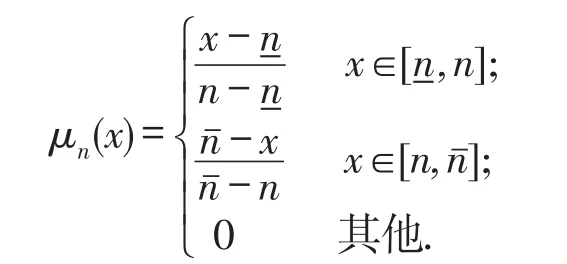
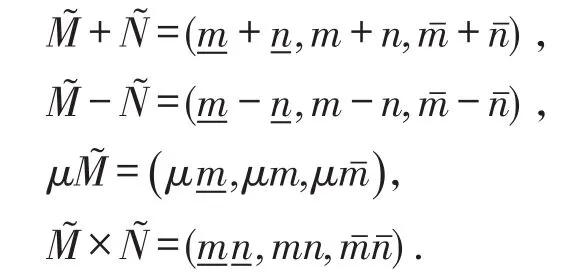
1.4 不同类型属性指标值归一化

（1）收益类模糊指标值的归一化

设有m个模糊指标值令如果是三角模糊数，记为bi,ci分别为的左右边界值；则归一化［3］的模糊指标值可写为

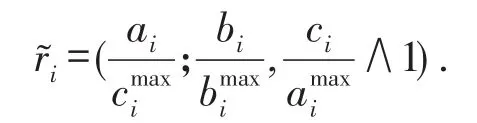
（2）成本类模糊指标值的归一化

设有m个模糊指标值如果是三角模糊数，记为分别为的左右边界值；则归一化的模糊指标值可写为

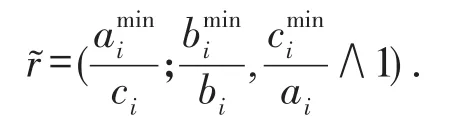
2 算法描述

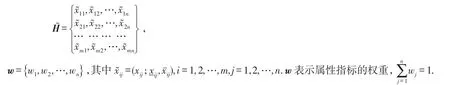
假定用于分类所用的决策模型中的效用函数u(x)是非线性的，即其中未知.

决策者从D中选取一个初始参照方案xr，令Cr={xr}，任取xi∈D决策者根据偏好进行判断，若xi劣于xr，令并将xi从D中排除，同时生成约束条件（ε为一个取定的小的正数）；若xi与xr无差异，将xi归放到Cr类中并从D中排除亦生成约束条件w∈Λ；若xi优于xr，则令同样把xi从D中排除并生成约束

决策者通过下面的决策模型对∀xk∈D与xr进行判断并分到相应的类别中：

其中w∈Λ，“*”表示"≥,=,≤".即

采用加权方法求解，上面的多目标线性规划可转换为：

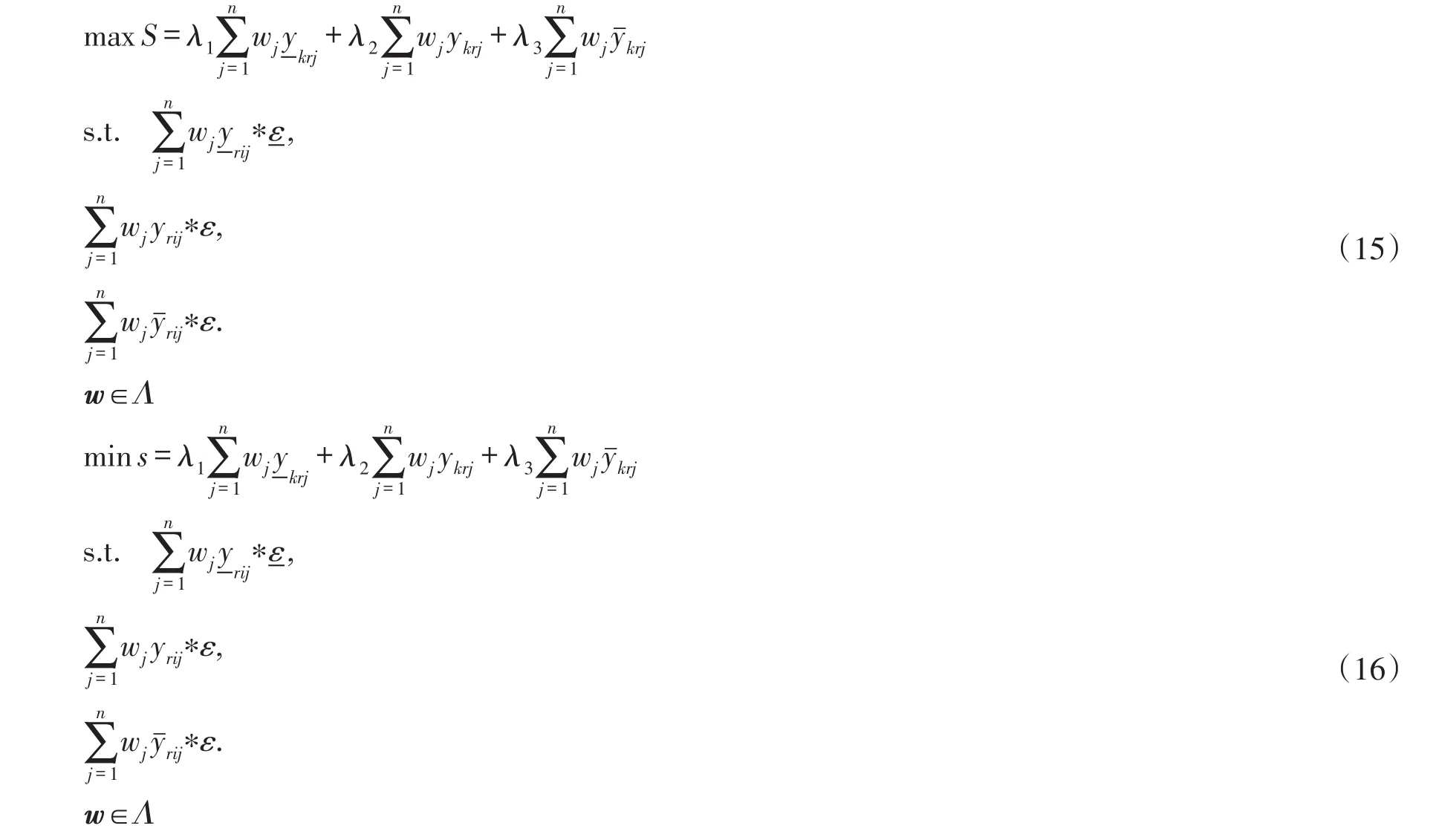
处理步骤如下：

第1步：任取xr∈D作为初始的参照方案，令Cr={xr}，Cl=∅，Cy=∅，K=1.

第2步：任取xi∈D，将xr与xi由决策者通过效用函数评判；若xi优于xr则转至第3步；若xi无差异于xr，则转至第4步；若xi优于xr则转至第5步.

第3步：令Cy=Cy⋃{xi}，生成约束条件若K≠1，将约束条件加入到规划（15）（16）的约束中，转至第6步.

第4步：Cr=Cr⋃{xi}，生成约束条件将约束条件加入到规划（17）（18）的约束中，转至第6步.

第5步：Cl=Cl⋃{xi}生成约束条件将约束条件加入到规划（15）（16）的约束中，转至第6步.

第6步：处理D中xk方案，求规划（15），若Smax≤-ε，再求解规划（16），若smin≤-ε则令Cl=Cl⋃{xk}，并在规划（15）（16）加入约束若Smax≥ε，令Cy=Cy⋃{xk}，并在规划（15）（16）加入约束w∈Λ；若令并在规划（15）（16）加入约束w∈Λ，否则将xk用其他方法处理.判别xk之后将其从D中删除.对D中其余方案同样 处理.

第7步：当D中所有方案处理完即可停止，否则令K=K+1，返回第2步.

按上面的方法步骤将D中方案被分为Cr、Cl和Cy三类.

3 算例

为了解学生的身体素质情况对云南师范大学本科学生体育锻炼等级以问卷的形式做详细调查，主要是锻炼行为及归因方式、心境的调查.对学生锻炼情况从外部身体的体能锻炼到内部心境的综合评定判断其等级情况.其中心境量表主要从紧张、愤怒、疲劳、抑郁、精力、慌乱、自尊这7个方面进行考量，现从统计表中抽取部分同学的心境指标值进行心境程度的分类.

现从众多问卷表中抽4人进行心境分类.用x1,x2,x3,x4和x5分别代表依次抽到的4位同学.方案集D=（x1,x2,x3,x4,x5）.

用xi=（xi1,xi2,xi3,xi4,xi5,xi6,xi7）表示第i位同学心境的7个属性的指标值.其中紧张、愤怒、疲劳、抑郁、慌乱属于成本类指标，精力和自尊属于收益类指标.由于问卷调查的调查项具有模糊性所以属性指标值用三角模糊数表示，这4位同学的模糊属性值矩阵如下:

由于指标的类型不同不便于直接应用决策模型，所以要用不同类型指标值的归一化方法进行归一化处理，处理如下：

由规划（15）和（16）决策模型进行抉择，运用LINGO.11求解.取x1为初始参照方案，根据体育心理测试的依据,x1的心境属于良.令Cr={x1}，再取x2由决策者与x1作比较，x2劣于x1，则令Cl={x2}，x2的心境为中等.把x2从D中删除同时生成约束条件

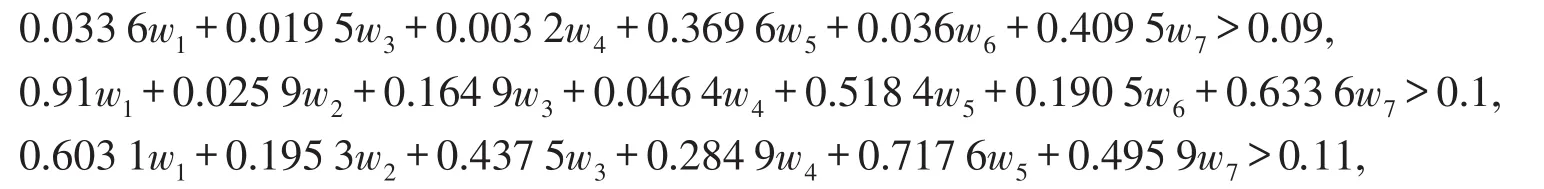
加入到（15）式,再取x3与x1进行比较规划如下：

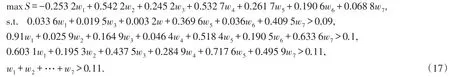
求解得Smax=0.501 9>0.1.即x3优于x1，把x3归并到Cy={x2}中则有Cy={x3}.x3心境为优.同时生成约束条件

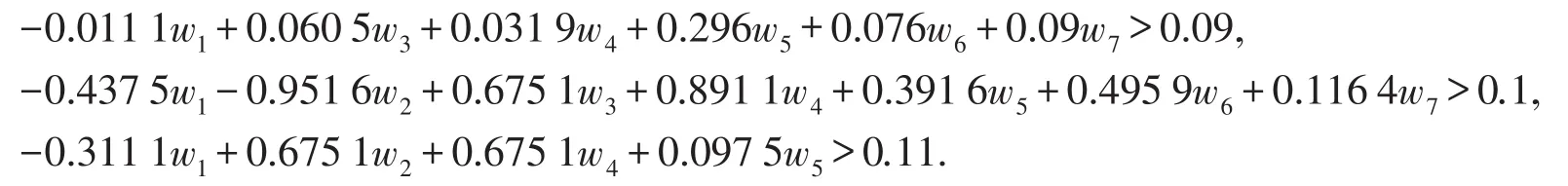
加入到新的规划（17）中，同样把x4与x1用如下规划进行比较

求解得Smax=-0.324 1<-0.1，再求解规划（16）得smin=-0.392 3<-0.1.则x4劣于x1，将x4归到Cl中则有Cl={x2,x4}.x4心境中等.同样把x5与x1用如下规划进行比较：

求解得Smax=-0.490 8<-0.1，再求解规划（16）得smin=-0.605 4<-0.1,则x5劣于x1.将x5归到Cl中则有Cl={x4,x5}.x5心境中等.此时D=∅，得到的分类结果为中等Cl={x2,x4,x5}，良Cr={x1}，优

4 总结

本文针对有限集的方案分类问题提出一种基于非线性的效用函数作为决策模型的目标函数的决策方法.该模型比线性的更能迎合决策者的需求条件，运用模糊理论把三角模糊数的规划转化为精确规划也更便于方案间的比较分类.模糊理论补充数学研究中严格精确的准则所不能解决的由不确定或模糊信息表述的问题.模糊理论通过隶属度，模糊数到精确数的转化，利用人类的智慧理解语言的模糊内含和外延，将各方面的知识互相转化.最后通过数值实例来运用和检验此模糊算法的可行性.

［1］BELLMAN R E，ZADEH L A.Decision making in a fuzzy environmen［tJ］.Management Science 17B，1970（4）：141-164.

［2］李荣均.模糊多准则决策理论与应用［M］.北京：科学出版社，2002.

［3］岳超源.决策理论与方法［M］.北京：科学出版社，2013.

［4］闫艳，赵宝福，岳立柱，等.基于效用函数的模糊数的比较与排序［J］.数学的实践与认识，2012，42（12）：70-76.

［5］郭嗣宗.模糊数比较与排序的结构元方法［J］.系统工程理论与实践，2009，6（6）：94-100.

［6］桑圣举，王炬香，杨阳.基于模糊多属性群决策的供应商分类方法研究［J］.机械设计与制造，2008（2）：226-228.

［7］张雯.基于多属性关联改进文本分类算法［D］.济南：山东师范大学，2011：9-10.

［8］徐泽水.一种交互式多目标决策新方法［J］.系统工程理论，2002，22（2）：104-108.

［9］BOUS G，FORTEMPS P，GLINEUR F，et al.ACUTA：Anovel method for additive function on basis of holistic preference statements［J］.European Journal of Operational Research，2010，206（2）：435-444.

［10］谢金星，薛毅.优化建模与LINDO/LINGO软件［M］.北京：清华大学出版社，2005.

A Classification Algorithm Based on Nonlinear Utility Function for Fuzzy Multiple Attribute Decision Making

JIANG Yingying，WANG Huiwen
（School of Mathematics，Yunnan Normal University，650500，Kunming，Yunnan，China）

A classification algorithm is presented based on nonlinear utility function and outranking relation which provides a decision making under fuzzy environment.This method use fuzzy theory which can transform the decision programmingwith triangular fuzzy number into common decision programming，andoperates with the weighted method which change multiple objective programming into single objective programming.Finally，an illustrative numerical example is provided to demonstrate the efficiency of the proposed method.

nonlinear utility function；fuzzy theory；triangular fuzzy number；weighted method

O 223

A

2095-0691（2017）02-0028-08

2016-12-05

云南省自然科学基金项目（2013FB034）

蒋莹莹（1990— ），女，安徽宿州人，硕士生，研究方向：决策分析.

王惠文（1975— ），男，江苏镇江人，博士，副教授，主要从事决策分析方面研究.