基于HollingIII型功能反应的具时滞捕食者-食饵系统的周期正解
2017-06-05安徽师范大学数学计算机科学学院安徽芜湖241002
冯 涛,梁 峰(安徽师范大学 数学计算机科学学院,安徽 芜湖 241002)
基于HollingIII型功能反应的具时滞捕食者-食饵系统的周期正解
冯 涛,梁 峰
(安徽师范大学 数学计算机科学学院,安徽 芜湖 241002)
利用拓扑度拓展定理研究一类带HollingIII型功能反应的具时滞非自治两种群捕食者-食饵系统,得到周期正解存在的一些充分条件.给出例子验证结论的有效性.
周期正解;捕食-食饵系统;拓扑度;HollingIII功能反应;扩散
0 引言
近年来,拓扑度拓展定理[1]被广泛应用于Lotka-Voterra系统的周期解存在性研究[2-4].文献[5]研究了如下基于比率的捕食者-食饵系统并得到了一些新的结果.
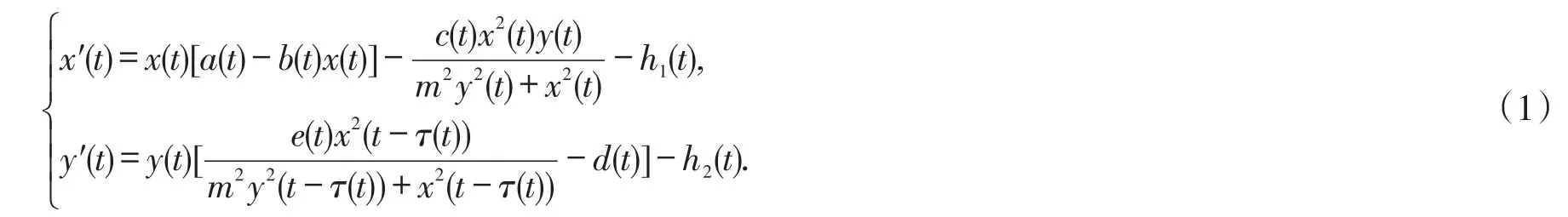
在生物数学领域,斑块种群生态学是一个热门的问题.当我们考虑到生物种群的生活习惯和迁徙特征时,在捕食者-食饵模型中我们需要增加表示种群从低密度斑块到高密度斑块的迁徙项D1(y(t)-z(t))和D2(z(t)-y(t)),其中y(t)和z(t)表示同一物种在不同斑块的种群密度.当第一个斑块中的种群密度大于第二个斑块中种群密度时,即y(t)>z(t)时,D1(y(t)-z(t))>0,D2(z(t)-y(t))<0,这时一部分种群从第二斑块向第一斑块迁徙;类似的,可以分析y(t) 本文考虑一类带HollingIII型功能反应的具时滞非自治两种群捕食者-食饵系统 其中xi(t)表示第i斑块的食饵密度,i=1,2,x3(t)表示捕食者密度.Di(t)表示食饵在第i斑块的扩散率,i=1,2,且函数a1(t),a2(t),b1(t),b2(t),D1(t),D2(t),c(t),d(t),e(t),f(t),τ(t)都是一些以ω为周期的非负连续函数,m>0是一个常数.上述涉及到的所有函数不恒等于0.这里 ai(t)(i=1,2)为食饵的内在生长率;m为半俘获饱和度;d(t)为表示捕食者的死亡率;c(t),f(t)为转换率;函数为在没有捕食者的状态下,食饵的增长率为反映捕食者捕获能力的功能反应函数. 本文的主要目的是研究系统(2)的ω周期正解存在性的充分性条件.为方便计,定义 其中f(t)是一个以ω为周期的严格正的连续函数.对于系统(2)做如下假设 为了证明主要结果,本文将应用重合度拓展定理给出一些引理.为此,先引入拓扑度的一些有关概念和重要结果. 定义1 设X和Y是Banach空间,L:D(L)⊂X→Y是一个线性映射,如果 (i)ImL是Y的闭子空间, (ii)dimkerL=codimImL<∞, 则L是一个指标为零的Fredholm算子. 若L是一个指标为零的Fredholm算子,令X1=kerL,Y2=ImL,则存在直和X=X1⊕X2,Y=Y1⊕Y2,那么存在连续映射P:X→X1,Q:Y→Y1. 从而可知L|kerP⋂D(L):(I-P)X→ImL是可逆的,且记它的逆为Kp. 定义2 设X和Y是Banach空间,Ω⊂X是一个有界开集,L:D(L)⊂X→Y是一个指标为零的Fred⁃holm算子,连续算子N:Ω⊂X→Y如果满足: 则称N在中是L-紧的. 因为ImQ与kerL是同构的,所以存在同构映射J:ImQ→kerL. 引理1(重合度拓展定理)[1]设X,Y为Banach空间,L为指标为零的Fredholm算子,Ω是X中的有界开集,N在上是L-紧的.假设下列条件成立: (3)deg{JQN,Ω⋂kerL,0}≠0,其中J:ImQ→kerL为同构映射. 则方程Lx=Nx在DomL⋂中至少存在一个解. 下面给出先验界估计的两个引理. 引理2 假设(H2)—(H3)成立且λ∈(0,1]为参数,u(t)=(u1(t),u2(t),u3(t))Τ是系统的一个ω-周期解.则其中R=R1+R2+R3,且 证明 由于u(t)=(u1(t),u2(t),u3(t))Τ是系统(3)的一个ω-周期解,下面只需要考虑u(t)在[0,ω]上的上下界.毫无疑问,存在ξi,ηi∈[0,ω]使得 显然 把系统(3)的第3个方程在[0,ω]积分得到 那么根据系统(3)和(5)式,有 由方程(3)和(4)知 为了给出u1(t)和u2(t)的上界,我们考虑如下两种情形. 情形I 如果u1(ξ1)≥u2(ξ2),则u1(ξ1)≥u2(ξ1).由(7)式知 下面,我们需要给出u1(t)和u2(t)的下界.根据(3)式的前2个方程以及(4)式有 证毕. 显然,引理2中的R1,R2,R3与λ无关.另一方面,考虑一个代数方程且获得如下结果. 引理3 假设(H1),(H4)及(H5)成立,μ∈(0,1]为参数,u=(u1,u2,u3)Τ∈R3是代数方程 证明 首先,由如下两种情形给出u1,u2的上界. 情形I如果u1≥u2,由(20)式的第一个方程知 定理1 假设条件(H1)—(H5)成立,那么系统(2)至少存在一个ω-周期正解. 证明 对系统(2)作如下变量变换 为了完成定理的证明,只需证明在定理1的条件下,系统(28)有至少一个ω-周期解.取 易见X,Y是两个带范数 的Banach空间.定义线性算子L和P,Q如下 通过简单计算,有 从而,由Lebesgue定理知,QN和Kp(I-Q)Nu连续.对于任意有界集Ω⊂X,利用Ascoli-Arzela定理容易验证紧.因此,有界.故,N在上L-紧. (i)由引理2,得到Lx≠λN(x,λ),对任意(x,λ)∈(∂Ω⋂DomL)×(0,1),条件(1)成立; (ii)由引理3,QN(x,0)≠0,对任意的x∈kerL⋂∂Ω,条件(2)成立; (iii)定义 其中μ∈[0,1]是一个参数.容易验证如果是一个常向量且由引理1,易得则从而,是一个同伦映射.由同伦不变性知 至此已经验证了引理1中的所有条件,故而系统(28)至少有一个ω-周期解.相应地,系统(2)至少有一个ω-周期正解.定理1证毕. 注1 由条件(H1)—(H5)及上述计算过程知,系统(2)所涉及函数周期ω可以为任一周期. [1]GAINES R E,MAWHIN J L.Coincidence degree and nonlinear differential equations[M].Berlin:Springer-Verlag,1977. [2]XIA Yonghui.Global analysis of an impulsive delayed Lotka-Volterra competition system[J].Commun Nonlinear Sci Num⁃er Simul,2011,16(3):1597-1616. [3]LU Shiping.On the existence of positive periodic solutions to a Lotka-Volterra cooperative population model with multiple delays[J].Nonlinear Anal,2008,68(6):1746-1753. [4]FANG Hui,XIAO Yongfeng.Existence of multiple periodic solutions for delay Lotka-Volterra competition patch systems with harvesting[J].Appl Math Model,2009,33(2):1086-1096. [5]FAN Yonghong,WANG Linlin.Multiplicity of periodic solutions for a delayed ratio-dependent predator-prey model with Holling type III functional response and harvesting terms[J].J Math Anal Appl,2010,365(2):525-540. [6]DU Chaoxiong,WU Yusen.Existence of positive periodic solutions for a generalized predator-prey model with diffusion feedback controls[J].Advances in Difference Equations,2013,2013(1):1-14. [7]CHEN Shihua,WANG Feng,YOUNG T.Positive periodic solution of two-species ratio-dependent predator-prey system with time delay in two-patch environmen[tJ].Appl Math Comput,2004,150(3):737-748. [8]CHEN Shihua,ZHANG Junhua,YOUNG T.Existence of positive periodic solution for nonautonomous predator-prey sys⁃tem with diffusion and time delay[J].J Comput Appl Math,2003,159(2):375-386. [9]CAO Meiyu,LI Xiaoping,DAI Xiangjun.Positive periodic solution for a two-species predator-prey system[J].Appl Math,2014,5(8):1099-1107. [10]XU Rui,CHEN Lansun.Persistence and stability for a two-species ratio-dependent predator-prey system with time delay in a two-patch environmen[tJ].Comput Math Appl,2000,40(4/5):577-588. [11]XU Rui,CHAPLAIN M,DAVIDSON F A.Periodic solutions for a delayed predator-prey model of prey dispersal in twopatch environments[J].Nonlinear Anal:RWA,2004,5(1):183-206. [12]DING Xiaoquan,WANG Fangfang.Positive periodic solution for a semi-ratio-dependent predator-prey system with diffu⁃sion and time delays[J].Nonlinear Anal,2008,9(2):239-249. Positive Periodic Solution for a Delayed Diffusion Predator-prey System with Holling Type III Functional Response FENG Tao,LIANG Feng In this paper,by using generalized continuation theorem based on coincidence degree theory,we study a non-autonomous two-species predator-prey system with Holling type III functional response and time delay.Some sufficient conditions for the existence of positive periodic solution are obtained. We give a specific example to illustrate the usefulness of the main results in the final section. positive periodic solution;predator-prey system;coincidence degree;Holling type III function⁃al response;diffusion O 193 A 2095-0691(2017)02-0009-10 2016-09-26 国家自然科学基金项目(11671013);安徽省自然科学基金项目(1308085MA08) 冯 涛(1993— ),男,安徽利辛人,硕士生,研究方向:泛函微分方程. 梁 峰(1974— ),男,安徽太和人,博士,副教授,研究方向:泛函微分方程.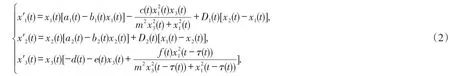
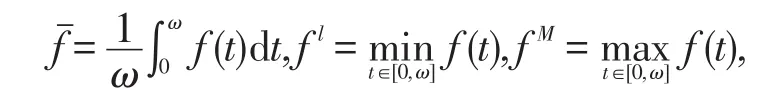
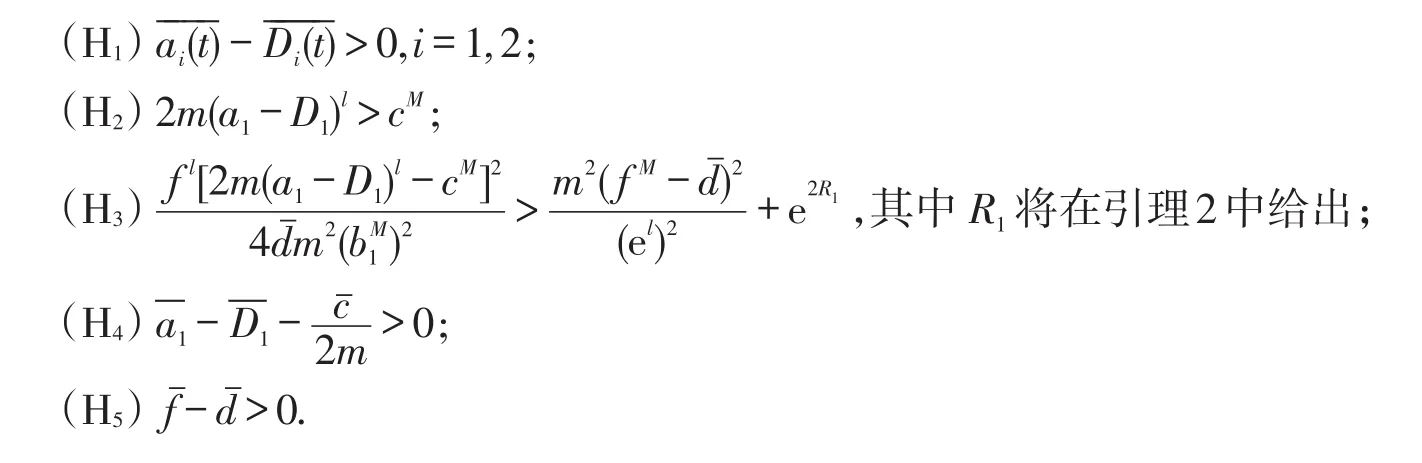
1 先验界估计
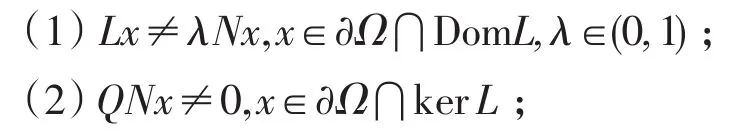
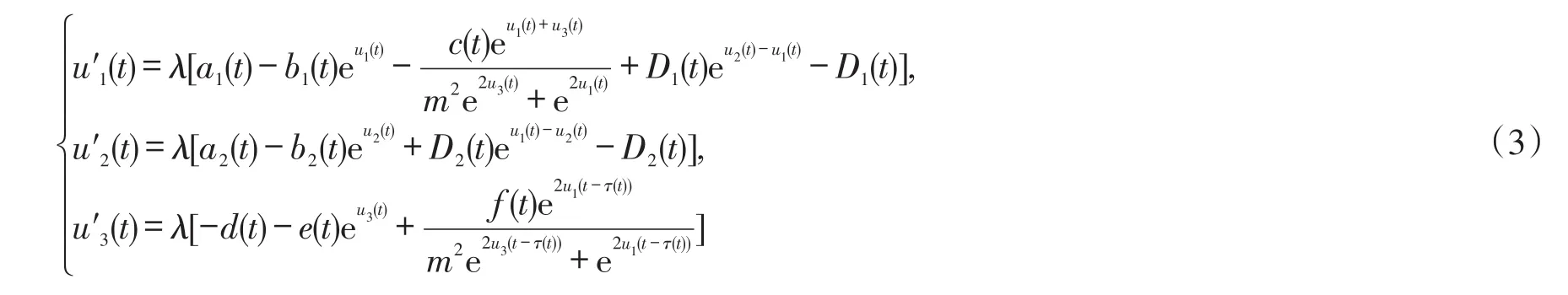
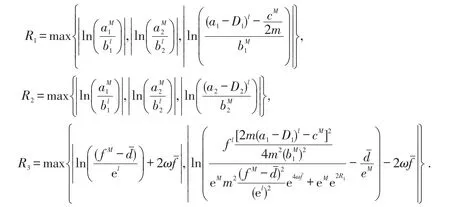
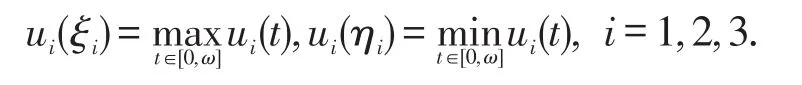


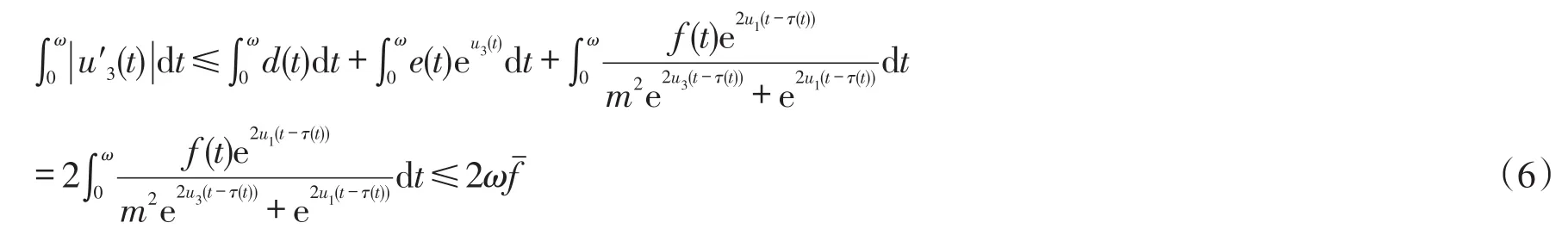
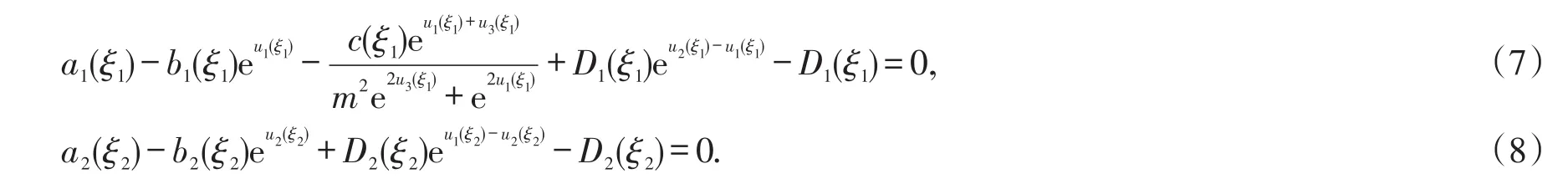





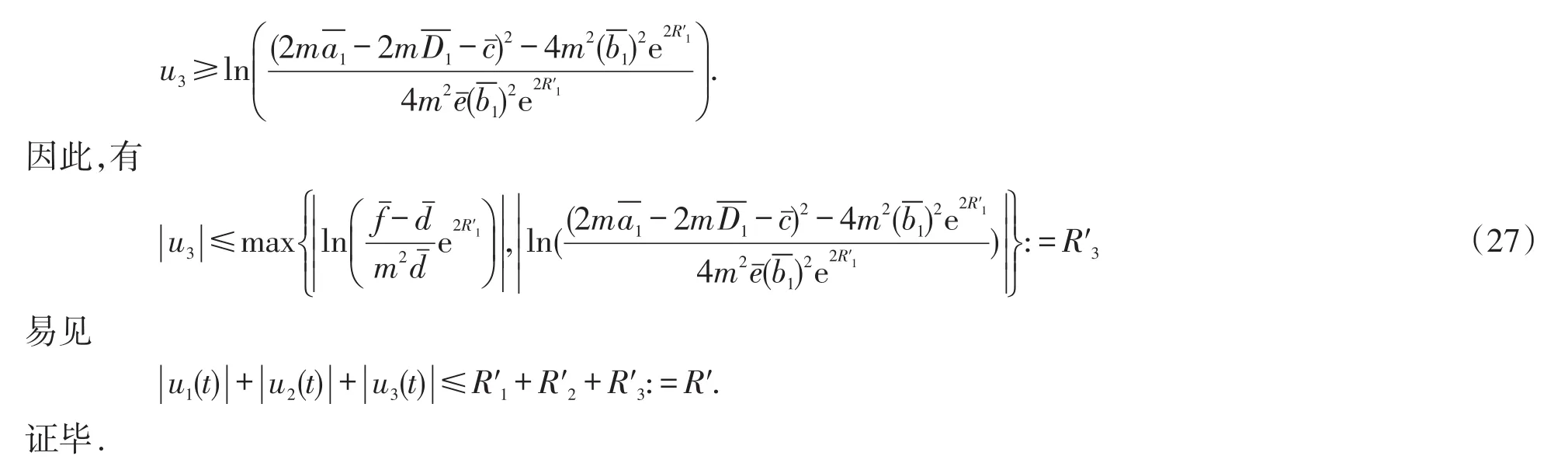
2 主要结果及证明
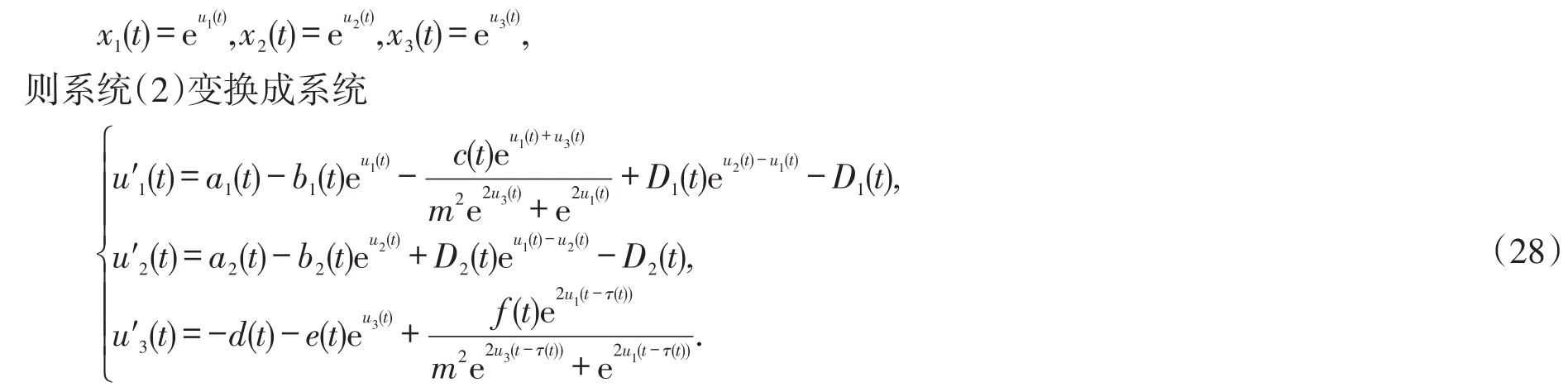
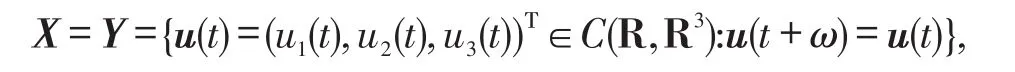
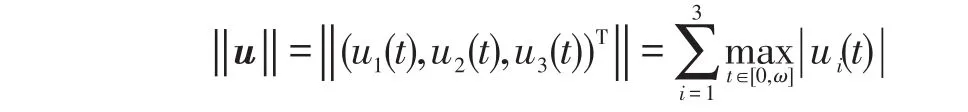
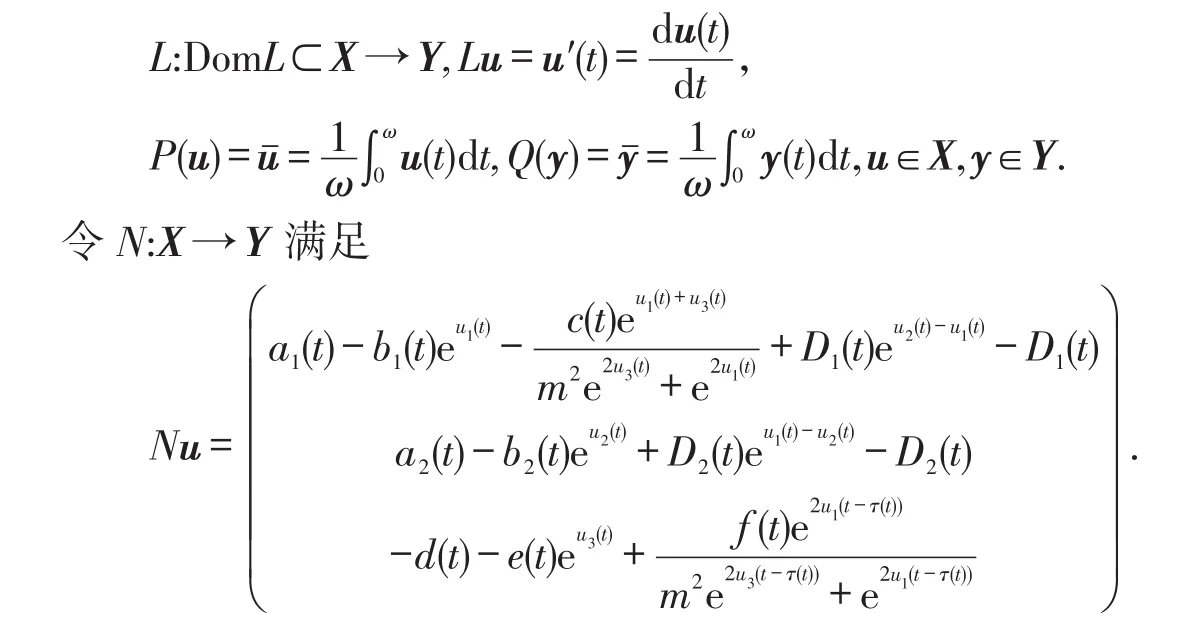
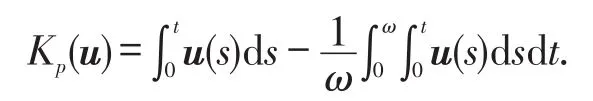
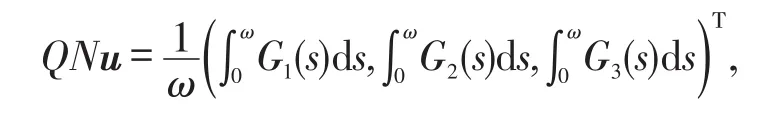
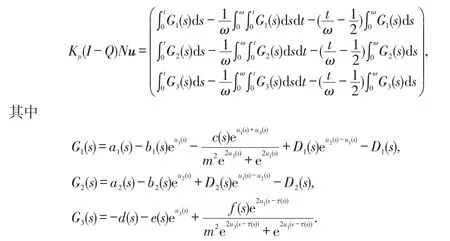
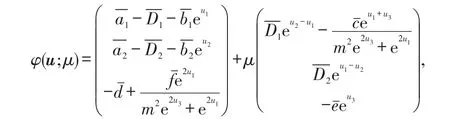

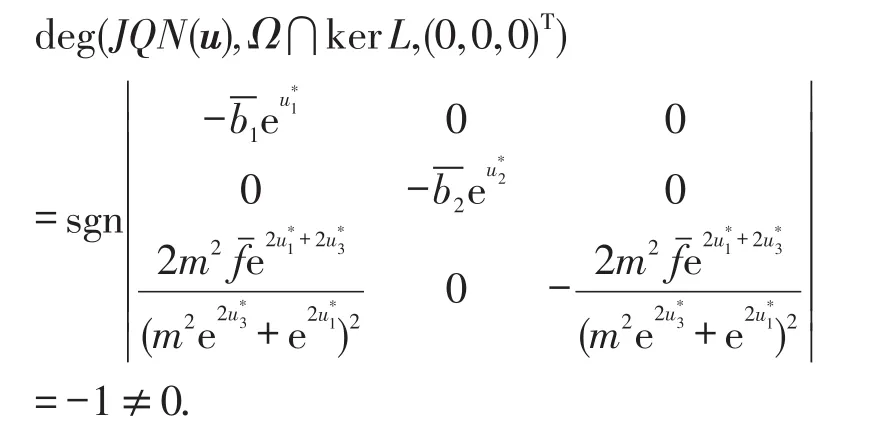
3 应用
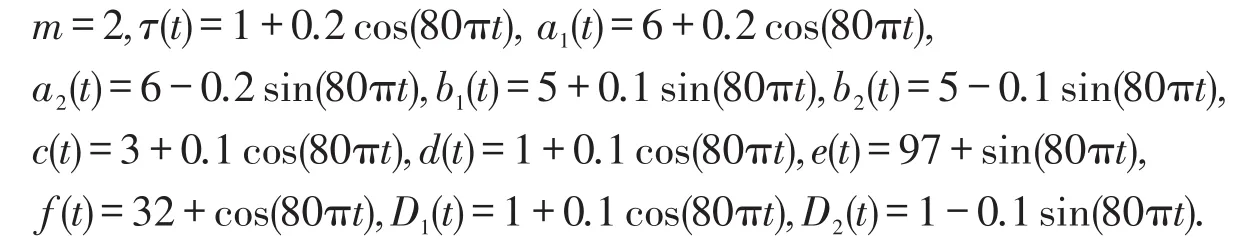

(School of Mathematics&Computer Science,Anhui Normal University,241002,Wuhu,Anhui,China)
