中学数学教学如何应对高考考试内容的变化以及核心素养的提出

常毓喜

（北京第四中学，北京 100034）

中学数学教学如何应对高考考试内容的变化以及核心素养的提出

常毓喜

（北京第四中学，北京 100034）

根据2017年高考数学考试大纲修订内容，以及核心素养即将在新的高中数学课程标准中的出现，高中数学教学如何应对这些变化，本文从突出基础性、重视能力培养、重视数学本质的教学及重视中国古代文化等方面，提出了一系列数学教学方法。

数学学科；考试大纲修订；核心素养；数学教学

从2014年9月3日国务院发布了《关于深化考试招生制度改革的实施意见》[1]开始，到全国各地纷纷出台新的招考方案，教育部考试中心发布高考2017年高考考试大纲，我国新一轮招生考试制度改革进入了高潮。这次改革的核心是坚持立德树人，适应经济社会发展对多样化高素质人才的需要，培养德智体美全面发展的社会主义建设者和接班人[2]。此次深化考试招生制度改革的目的，是从有利于促进学生健康发展、科学选拔各类人才和维护社会公平出发，为办好人民满意的教育、建设人力资源强国提供有力保障，为实现“两个一百年”奋斗目标和中华民族伟大复兴的中国梦提供强有力的人才支撑。

将“发展学生核心素养体系”的研制与构建作为推进课程改革、深化发展的关键环节，发展学生的核心素养是育人的重要目标。近几年的高考数学试题不仅坚持社会主义核心价值观，坚持立德树人，关注社会发展，关注考生社会责任的培养，体现时代特征，很好地实现了课程标准和考试大纲的内容和要求，体现能力立意，弘扬数学文化，还突出对创新应用能力的考查，深入考查考生的逻辑思维能力和实践能力，注重体现数学的理性价值和科学价值，对培养学生的创新精神、实践能力，提升学生核心素养的数学课程教学改革有积极的导向作用。

1 2017年高考数学考试大纲修订的主要内容

2017年高考数学考试大纲的修订与前几年相比力度较大，主要有以下两大变化：一是明确提出从数学思想方法、数学能力、数学的科学与人文价值3个方面考查学生的数学学习情况，体现知识与能力并重、科学与人文兼顾的精神，明确提出在数学考试中增加数学文化的要求，有利于实现全面提升和培养学生综合的数学素养的目的。二是进一步强化数学学科体系结构，在数学考试大纲中删去选考模块4-1“几何证明选讲”[3]。这既符合中学教学的实际情况，又保持了与数学教学大纲和即将修订后的课程标准的一致性，更有利于中学数学教学和复习备考。

2 高中数学核心素养的含义及分析

数学核心素养是具有数学基本特征的、适应个人终身发展和社会发展需要的人的思维品质与关键能力，是数学课程目标的集中体现，它是在数学学习的过程中逐步形成的。数学核心素养包括数学抽象、逻辑推理、数学建模、数学运算、直观想象、数据分析。这些数学核心素养既有独立性，又相互交融，形成一个有机整体[3]。

数学抽象是指舍去事物的一切物理属性，得到数学研究对象的思维过程。数学抽象使得数学成为高度概括、表达准确、结论一般、有序多级的系统。

直观想象是指借助几何直观和空间想象感知事物的形态与变化，利用图形理解和解决数学问题的过程。直观想象是发现和提出数学问题、分析和解决数学问题的重要手段，是探索和形成论证思路、进行数学推理、构建抽象结构的思维基础。

数学抽象与直观想象体现了数学的一般特性。

逻辑推理是指从一些事实和命题出发，依据规则推出其他命题的思维过程。逻辑推理是得到数学结论、构建数学体系的重要方式，是数学严谨性的基本保证，是人们在数学活动中进行交流的基本思维品质。

数学运算是指在明晰运算对象的基础上，依据运算法则解决数学问题的过程。数学运算是解决数学问题的基本手段。数学运算是一种演绎推理，是计算机解决问题的基础。

逻辑推理与数学运算体现了数学思维的严谨性。

数学建模是对现实问题进行数学抽象，用数学语言表达问题、用数学知识与方法构建模型解决问题的过程。数学建模搭建了数学与外部世界的桥梁，是数学应用的重要形式。数学建模是应用数学解决实际问题的基本手段，也是推动数学发展的动力。

数据分析是指针对研究对象获取相关数据，运用统计方法对数据进行整理、分析和推断，形成关于研究对象知识的过程。数据分析是研究随机现象的重要数学手段，是大数据时代数学应用的主要方法，已经深入到现代社会生活和科学研究的各个方面。

数学建模与数据分析体现了数学的实用性。

3 中学数学课堂教学如何应对核心素养以及考试内容的变化

3.1 中学数学课堂教学要突出基础性

高考数学考试大纲指出，数学科的命题在考查基础知识的基础上，注重对数学思想方法的考查。所以在教学中要突出基础性，重视基本概念、基本定理公式与基本技能的教学。

3.1.1 要重视基本概念的教学

教学中要特别重视基本概念的教学，要从概念的定义出发，由表及里，去伪存真，掌握概念的本质属性，这是提升数学素养的必要条件。

例1命题：“若（x-1）（x+2）=0，则x=1”的否定是__________．

很多人认为命题的否定就是否定命题的结论，所以“若p则q”的否定就是“若p则¬q”，其实这种理解是错误的。如果按照这种理解，上述命题的否定就是“若（x-1）（x+2）=0，则x≠1”，这个结果显然是错误的，因为这个命题与原命题都是假命题。

我们来看看教材中“命题的否定”的定义：

人教A版：对一个命题p全盘否定，就得到一个新的命题，记作¬p，读作“非p”或“p的否定”。

人教B版：对命题p加以否定，就得到一个新的命题，记作¬p，读作“非p”或“p的否定”。

根据上述定义及符号语言可以看出，命题的否定是对整个命题的否定，而非只对其结论进行否定。因此这个命题的否定就应该是“并非对（x∈R，若（x-1）（x+2）=0，则x=1”，也即“存在x∈R，使（x-1）（x+2）=0，且x≠1”。

此外，在概念教学中还要避免模式化，避免机械套用有关结论。

例2命题：“存在无穷多个正整数n，使得成立”的否定是（ ）.

A.对任意正整数n，都有成立

B.对任意正整数n，都有

C.存在无穷多个正整数n，使得成立

D.至多有有限个正整数n，使得成立

通过上面的例题可以看出，教学中必须注重概念定义的教学，务必让学生熟悉概念的定义，能够利用概念的定义解决有关问题。

例3如图1所示，直线y=kx+m与曲线y=f（x）相切于两点，令F（x）=f（x）-kx，则F（x）有___个极大值点.

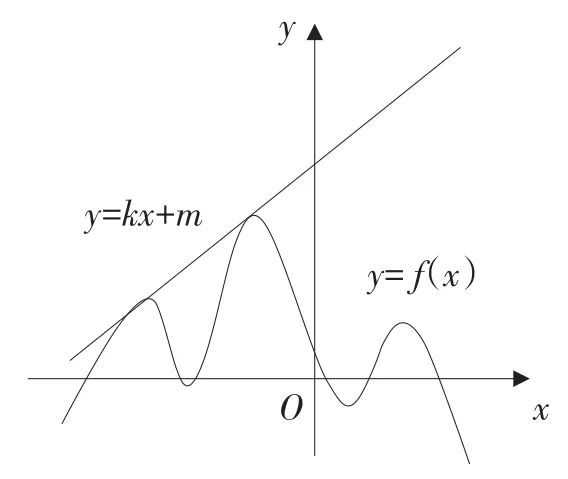
图1

此题很容易想到利用导数解决，往往由于得不到函数的解析式而作罢，其实本题就是考查极值这个概念的，只要对极值这个概念的本质属性比较了解，再根据两个函数的函数值的变化情况，很容易就可以得到结果。

例4为了解本市居民的生活成本，甲、乙、丙3名同学利用假期分别对3个社区进行了“家庭每月日常消费额”的调查.他们将调查所得到的数据分别绘制成频率分布直方图（如图2所示），记甲、乙、丙所调查数据的标准差分别为s1，s2，s3，则它们的大小关系为________.

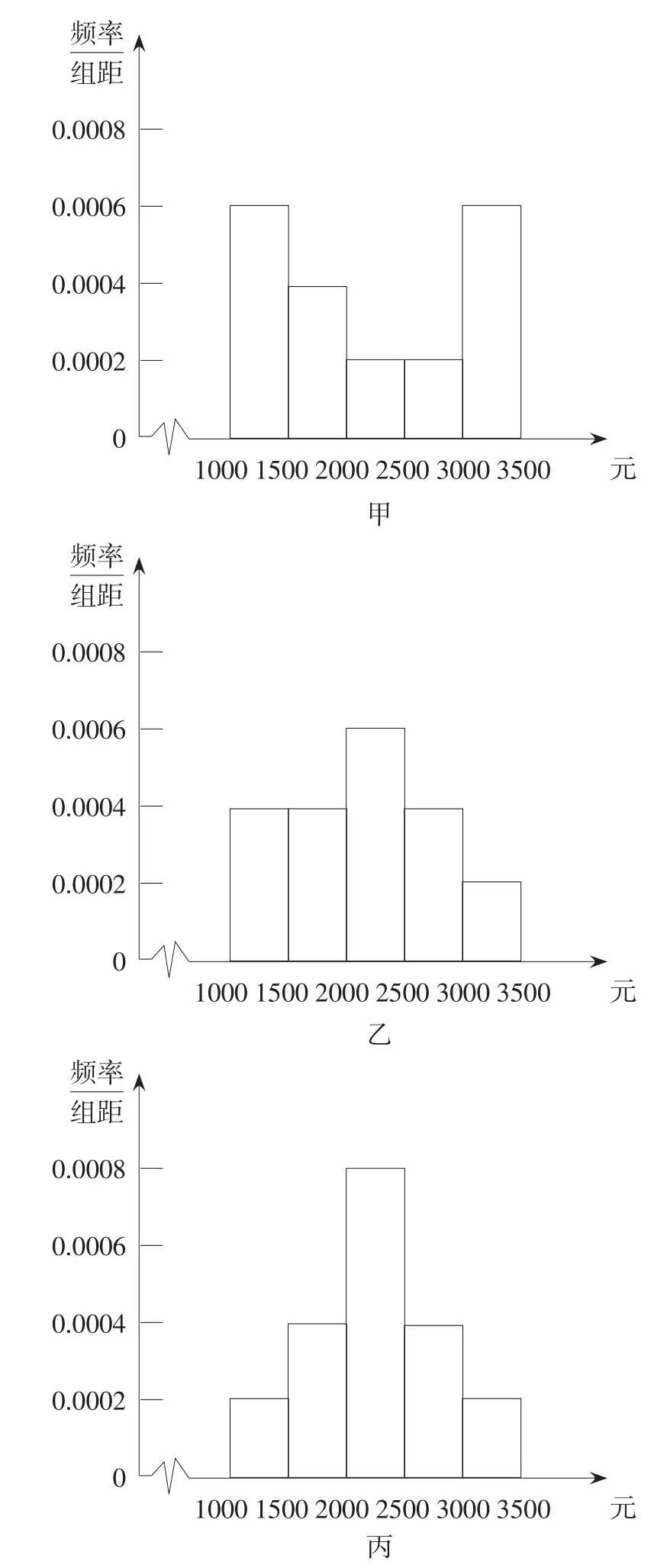
图2

很多人认为，方差与标准差是反映数据波动情况的特征数，因此标准差小的图像就比较“平”，标准差大的图像就“起伏比较大”，根据这个理解，乙同学调查所得到的数据的标准差最小。其实根据方差与标准差的定义，这两个特征数的本质属性是相对于平均数来说，标准差比较小的，集中在平均数附近的数比较多；反之，集中在平均数附近的数就比较少。因此很明显，正确的结论是丙同学调查所得到的数据的标准差最小，甲同学调查所得到的数据的标准差最大。

由此可见，教学中不仅仅要注重对概念的定义的理解与记忆，更重要的是要通过概念的定义分析挖掘概念的本质属性，充分理解概念的内涵，这样才能适应当前的形势，提高学生的数学素养，特别是数学的核心素养。

3.1.2 要重视基本定理公式的教学

基础知识的另一个重要内容就是高中数学中重要的定理公式。当前的课堂教学存在重应用轻推导的现象，就是只重视定理公式的应用，而忽视公式的推导、定理的证明。事实上，在教学中重视公式的推导、定理的证明，不仅有利于理解与掌握定理和公式，理解公式之间的相互关系，而且还可以进一步挖掘公式中蕴含的数学思想，从而成为我们解决有关问题的敲门砖。

比如点到直线距离公式的教学，包括教科书在内基本上都舍弃了解析法，即“求出过点P与直线l垂直的直线PQ的方程，然后求出点Q的坐标，最后利用两点间距离公式求出PQ的长”的方法，普遍认为上述方法虽然思路自然，但具体运算需要一定技巧。其实利用上述方法，运算量并不是大到不可接受，如果方法得当，学生一定对解析法印象深刻，并会在有关问题中应用解析法解决问题。这也正体现了解析几何的本质，即利用代数方法（方程、坐标）解决几何（曲线）的有关问题。

因此，在教学中充分展示知识的发生发展过程，充分挖掘知识的内涵，对培养学生的核心素养无疑是有好处的。

3.1.3 要重视基本技能的教学

基本技能是数学基础知识的重要组成部分，在数学建模、数学运算以及数据分析等核心素养中都有它的影子，也是历年高考考查的重点。在教学中对基本技能的教学，主要包括掌握入手点、了解隐藏点与熟悉易错点。

所谓掌握入手点，就是要掌握基本思想方法，通过分析其本质特征，熟练掌握其适应范围，掌握基本问题的基本解法。所谓了解隐藏点，就是要了解哪些知识有隐藏的漏洞，必须与哪些知识配合使用才能避免产生错误。如在解析几何中解决直线与圆锥曲线相交的问题时，如果使用了韦达定理，就必须检验判别式是否大于零，否则就可能出现直线与圆锥曲线没有交点的情况。所谓熟悉易错点，就是指在教学中我们应该重视那些学生容易出现错误的方面，如忽略函数的定义域、数列中没有注意n的取值范围等问题而导致错误，这些虽然不难掌握，但是如果不注意很容易出现错误。这也体现了数学核心素养中逻辑推理的严谨性。

3.2 中学数学课堂教学要重视能力的培养

2017年考试大纲修订虽然在考查内容中删去“几何证明选讲”模块，但并不意味削弱了对推理论证能力的考查，修订后的大纲强调对推理论证能力和抽象概括能力的考查贯穿于全卷，是考查的重点。数学能力是综合的能力，其培养训练应体现在数学教学的全过程，对数学各种能力的考查应体现在数学学科完整的知识体系中。

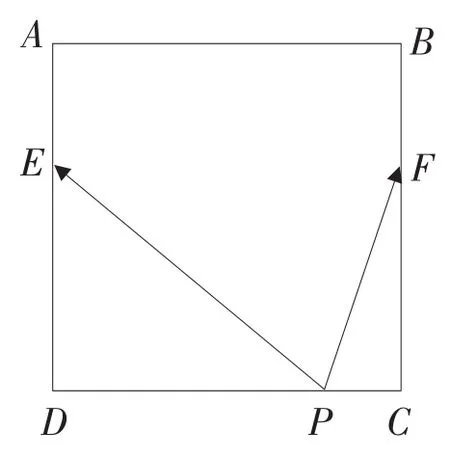
图3

中学数学课堂教学要重视对学生能力的培养，特别是逻辑思维能力和推理论证能力的培养。培养能力的方法有多种，如培养阅读能力就要多进行阅读，提高运算能力就要多进行运算，而逻辑思维能力和推理论证能力的培养则要靠思考。而要想让学生能有效的思考，教师的设问就很重要。

阿尔布西埃德，国籍阿曼，1973年生于阿曼马斯喀特。1994年开始摄影工作，自2007年以来一直为阿曼美术学会摄影俱乐部主席，阿曼驻国际摄影艺术联合会联络官员。在许多地方和国际摄影比赛中获得若干奖项，最喜欢肖像和风景摄影。

例5如图3所示，正方形ABCD的边长为6，点E，F分别在边AD，BC上，且DE=2AE，CF=2BF.如果对于常数λ，在正方形ABCD的四条边上，有且只有6个不同的点P使得成立，求λ的取值范围.

对于这道题目可以进行以下设问：

设问1：如何才能求出λ的取值范围呢？（设法得到关于λ的不等式）

设问2：在正方形ABCD的四条边上，有且只有6个不同的点P使得成立是什么意思？（动点P的轨迹与正方形ABCD的四条边有6个交点）

通过上述设问，引导学生进行思考，而学会思考、学会研究是提升逻辑思维能力和推理论证能力的重要途径。

例6如果存在正整数ω和实数φ使得函数的图像如图4所示（图像经过点（1，0）），那么ω的值为____.

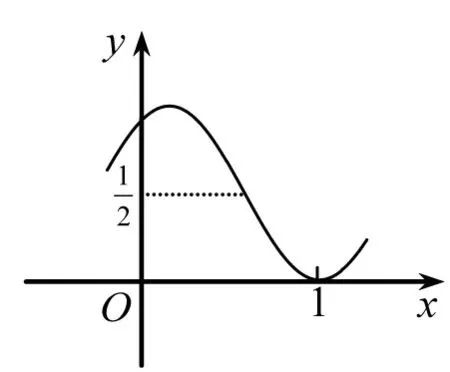
图4

设问1：如何求未知数ω的值？（设法得到关于ω的方程）

设问2：两个未知数需要两个方程才可能求出它们的值，而此题我们只能得到一个方程，怎么办？

设问3：注意到ω是正整数，因而通过范围就可以求出其值，那么如何能得到关于ω的不等式呢？

通过以上设问，应该容易想到通过函数的图像可以得到关于周期的不等式，从而得到关于ω的不等式，问题得以解决。

在教学中，也可以把数学思想与核心素养的提升有机地结合起来。

例7甲、乙、丙、丁4人参加数学竞赛，4人在成绩公布前作出如下预测：

甲预测说：获奖者在乙、丙、丁3人中；

乙预测说：我不会获奖，丙获奖；

丙预测说：甲和丁中有1人获奖，丙获奖；

丁预测说：乙的预测是对的.

成绩公布后有两人获奖，且4人中有两人的预测与结果相符，另外两人的预测与结果不符，则获奖的是_______.

因为已知有两人的预测与结果相符，所以可以把乙、丁分为1组，利用乙的预测是否正确进行分类，利用分类与整合的数学思想进行思考，即可得到正确结果。

这就是把数学思想与核心素养相结合的一个很好的例子，以此培养学生的能力，效果一定不错。

有效的设问可以充分发挥教师的主导作用，引导学生学会思考是提升能力的重要手段。教学中要精心设计问题，有的放矢，贴近学生的最近发展区，就可以提高课堂教学效率，打造高效课堂。

3.3 中学数学课堂教学要重视数学本质

数学核心素养中的数学抽象是数学的基本思想，是形成理性思维的重要基础，反映了数学的本质特征，贯穿在数学知识的产生、发展、应用的全过程中。

导数既是函数的一个重要概念，同时也是研究函数性质，解决函数有关问题的一个重要工具。教学中不仅仅要重视导数的概念、运算以及应用，还要突出导数的工具性，突出导数在研究函数的有关性质、解决函数有关问题时的工具作用。

（2）证明：对于任意的x1，x2∈（0,+∞）都有成立.

下面给出第（2）小题的3种解法。

所以x1，x2∈（0,+∞）时

有人会觉得此题有超纲的嫌疑（因为有二阶导数的影子），但其实恰恰这是一道“好题”，因为它充分体现了导数的工具作用，第（2）小题的3种解法中，无论哪种方法都是利用导数作工具，充分研究了函数的性质，特别是单调性，并利用函数的这些性质解决问题。我们在教学中就要多选择这样的题目，发挥题目导向作用，渗透应用意识，发展实践能力。

3.4 中学数学课堂教学要重视中国古代文化、应用意识与实践能力

近几年的高考试题高度重视传统文化对于立德树人的独特功能，加大力度弘扬和考查中国优秀传统文化，体现了高考为国选才的重大使命。增加对中国传统文化进行考查的内容，将中国古代文明作为试题背景材料，体现中国传统文化对人类发展和社会进步的贡献。

例9《九章算术》是我国古代内容极为丰富的数学名著，书中有如下问题:“今有圆堡壔（dǎo），周四丈八尺，高一丈一尺.问积几何？答曰：二千一百一十二尺.术曰：周自相乘，以高乘之，十二而一.”这里所说的圆堡壔就是圆柱体，它的体积为“周自相乘，以高乘之，十二而一”.就是说：圆堡壔（圆柱体）的体积为（底面的圆周长的平方×高）.在上述公式中圆周率π的取值为____.

这个题目虽然难度不大，但是立意新颖，富有创新精神，特别是巧妙地利用我国优秀的传统文化设计试题，不仅使学生对我国的传统文化有所了解，同时也考查了学生的各种能力，如阅读能力、思维能力、运算能力、数据处理能力等，很好地渗透了数学的核心素养。与当前高考考试内容改革坚持立德树人，紧紧抓住教育发展“培养什么人、怎样培养人”的实质和核心，不仅要考查学生的知识和能力，还要把社会主义核心价值体系融入考试内容等高度一致。

当前，我国的新一轮教育改革进入了一个新的高潮。我们必须深入研究这次改革的特点，并在工作中贯彻落实有关精神，积极应对，使教学适应改革的需要，提高教学的有效性与针对性。

[1]国务院.关于深化考试招生制度改革的实施意见[EB/OL].（2014-09-03）[2016-11-20].http://www.gov.cn/zhengce/content/ 2014-09/04/content_9065.htm.

[2]教育部.关于全面深化课程改革，落实立德树人根本任务的意见[EB/OL].（2014-03-30）[2016-11-22].http://www.moe.edu.cn/ publicfiles/business/htmlfiles/moe/s7054/201404/167226.html.

[3]教育部考试中心.突出实践性和创新性实现高考的选拔功能——2016年数学高考试题评析[J].中国考试,2016（7）:12.

Changes in the Content of the Math Exam for College Entrance and the Curriculum Standards’Key Competencies Requirement:Challenges and Solutions

CHANG Yuxi
（Beijing No.4 High School,Beijing 100034,China）

The promulgation of revised mathematics curriculum standards,along with the upcoming introduction of new experimental mathematics textbooks and especially the revision of the mathematics examination syllabus,has greatly changed the environment of mathematics education.How do we deal with this in the classroom teaching of the subject in order to adapt as soon as possible to the needs of the situation?This is a question every mathematics teacher needs to think about.This article,in response to the question,offers a series of mathematics teaching methods from the aspects of emphasizing the basics,paying attention to the cultivation of ability,attaching importance to the teaching of mathematics essence and paying attention to Chinese ancient culture.

Academic Subject of Mathematics;Revision of the Exam Syllabus;Key Competencies;Mathematics Teaching;Civil Service System

G405

A

1005-8427（2017）02-0052-7

10.19360/j.cnki.11-3303/g4.2017.02.008

（责任编辑：周黎明）

常毓喜（1966—），男，北京第四中学，数学特级教师。