实时监控计算机自适应考题的两种方法及其稳健性比较
2017-06-05张金明曹灿兮揭勇菁
张金明 曹灿兮 揭勇菁
(美国伊利诺伊大学香槟分校,美国伊利诺伊州 61822)
实时监控计算机自适应考题的两种方法及其稳健性比较
张金明 曹灿兮 揭勇菁
(美国伊利诺伊大学香槟分校,美国伊利诺伊州 61822)
基于项目反应理论和基于经典测量理论的两种序贯监控方法,用来实时监控计算机自适应考试,及时侦测出已泄露试题,并替换或剔除泄露试题,以提高考试的公正性和分数的有效性。本文着重对这两种序贯监控方法在考生整体能力水平随时间有季节性变化或具有连续提高趋势的情况下进行统计稳健性比较,主要考察这两种监控方法犯第一类统计错误的概率是否变大,是否超出预设的显著性水平。模拟结果表明,基于项目反应理论的序贯监控方法在本文所考虑的情况下比基于经典测量理论的方法具有更好的稳健性。
计算机自适应考试;经典测量理论;项目反应理论;试题曝光率;变点问题;序贯监控方法
1 引言
计算机自适应考试(Computerized Adaptive Test,CAT)是一种现代考试形式,它依靠大型题库,采用现代测量理论,根据每个考生不同的能力水平,用计算机自动选择难度恰当且统计性能优良的题目,生成为其量身定做的试题组合,从而实现对考生的高效测量[1]。依靠现代测量理论,计算机自适应考试与传统纸笔测验相比,可使用更少的试题并得到更精确的考生能力估计值。
由于在一次考试中,计算机组卷所使用的试题均来自同一题库,在该题库被使用一段时间后,其中的一部分题目就有可能被泄露,所以一直以来,计算机自适应考试都面临着试题安全问题,先行参加考试的考生可能会泄露试题信息,使得后续考生成为“受益者”[2-9]。一旦试题被泄露,相应试题的统计特性将被改变,对于后续的“受益”考生,这些试题难度变低,故“受益”考生的能力值会被高估,这将威胁考试的公正性和分数的有效性。Zhang等在一个模拟研究中指出,当一个720道题的题库中有150道试题被泄露时,考生能力估计值的偏差和误差均方根分别高达1.010和1.226[9]。
试题曝光率是衡量考试安全性的一个重要指标。通常,一道试题被使用得越频繁(即其曝光率越高),被泄露的可能性就越大。因此,在计算机组卷选题过程中,研究人员就会运用一些试题曝光控制的方法,平衡试题曝光率以加强考试安全性[4,7,10-15]。基于对考试安全性的考虑,题库中一些曝光率较高的试题会被暂时或永久剔除[16]。但是,高曝光率的试题不一定就是被泄露的试题,同时低曝光率的试题也有被泄露的可能。例如,虽然一道试题被很多个考生使用,即曝光率较高,但如果这些考生都没有在考后分享试题,那么这道试题并没有被泄露;反之,另一道试题虽然没有被经常使用,曝光率较低,但恰被用在一个习惯于在考后分享试题的考生的考试中,那么这道题就很可能被泄露。因此曝光率的高低并不能准确判断一道试题是否被泄露。
另一个考试安全性的指标是测验重叠率,常被用以侦测大规模试题泄露问题[2-3,7,17]。尽管有这两种指标已初步保障考试安全性,但在计算机自适应考试进行过程中,仍需要统计技术对试题统计特性进行实时连续监控,并在试题泄露发生时及时侦测到这些已泄露试题。
为加强计算机自适应考试的安全性及分数的有效性,并在计算机自适应考试过程中实现对试题的实时连续监控,以尽早侦测出已泄露试题,Zhang[18]和Zhang&Li[19]开发出两种实时连续监控试题的统计序贯监控方法,一种是基于经典测量理论(Classical Testing Theory,CTT),另一种是基于项目反应理论(Item Response Theory,IRT)。两种方法都是在考试过程中通过一系列统计假设检验来判断试题的统计特性是否发生显著变化。本文将从理论框架、模拟研究及研究结果对这两种方法进行详细介绍,并在考生整体能力水平随时间有季节性变化或连续提高趋势的情况下,对这两种方法进行统计稳健性的比较。
2 序贯监控方法
通常一个题库会使用较长一段时间,考试管理者需要监测每一道被使用多次的试题。假定{U1,U2,…,Un…}是某一被监控试题的得分序列。这里及本文后面的n是指作答某试题的第n个考生,而不是指参加考试的第n个考生。若第n个考生答对该题,则Un=1;反之,则Un=0。注意,n是与试题相关的,对于不同试题,相同的n并不一定是同一个考生。为方便起见,本文对所有与试题相关的变量和函数都没有用试题下标。因为监控程序是对每一道被使用多次的试题分别监测的,所以不用试题下标不会产生歧义。
2.1 变点问题
如果一个随机变量在某一时间点之前服从一个分布,而在这一时间点之后服从另一个分布,这在统计序列分析中称作变点问题[20-26]。变点问题出现在众多领域,尤其是在工业产品质量监控中。在连续的生产过程中,机器在任一时间点都可能发生故障,从而导致产品质量下降(产品特征变量在该时间点发生变化),因此需要一个监控方法来甄别产品质量。理想的监控方法是在产品质量发生变化时,及时发出信号,同时把犯第Ⅰ类侦测错误率控制在一定水平之下。这里,第Ⅰ类侦测错误是指在产品质量未发生改变时,该监控方法错误地判断产品质量已发生变化。
若该试题的信息在第nc个考生后被泄露,即部分将要参加考试的考生得到了该试题的信息,那么该试题对于这些考生来说将会变得简单。对于这些考生,新的正确作答该题的概率为而更极端的情况是这些考生将会一直答对这道题,即而那些没有得到该题信息的考生仍将以的概率正确作答该题。当该试题被选中给一个考生,依赖于该考生是否在考试前已获得该试题的信息,这个考生正确作答该题的概率可能是,也可能是假定这个考生恰好得到了该题信息的可能性概率是r,那么根据全概率公式,任何一个考生在试题泄露之后答对该题的概率为
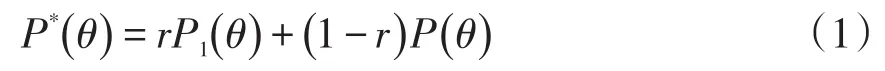
显然,r与得到该题信息的考生在所有将要参加考试的考生中的比例密切相关。因此,r可以看作该题泄露影响广度的指标,而更确切地说可以看作该题泄露影响深度的指标。当然r是未知的,但在本文所介绍的方法中我们并不需要估计它的数值。如果r=0,即该题的泄露影响可忽略,不造成任何损失,或者说该题并没有被泄露,所以考试管理者并不需要考虑该题的泄露问题。因此,本文只考虑r>0的情况,这样
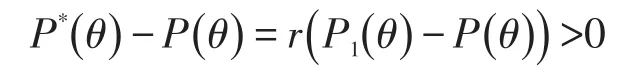
即在统计上看该试题在泄露之后对所有的考生来说都显得简单了。总之,在试题泄露之前,该试题服从一个项目反应函数而在试题泄露之后,它服从另一个较大的项目反应函数因此,试题泄露问题是一个变点问题。
一道试题是否被泄露是未知的。如果泄露,其变点nc的位置更是难以确定。而且,不同的试题,它们的被泄露变点位置不一定是一样的。因此,需要统计方法对每一道试题进行实时连续监控,一旦发生试题泄露,尽早地甄别出已泄露试题,以保障计算机自适应考试的安全性和有效性。
假设某被监控试题的变点是nc,而监控结果表明该试题在被n个考生使用过后被泄露(如图1所示)。若n
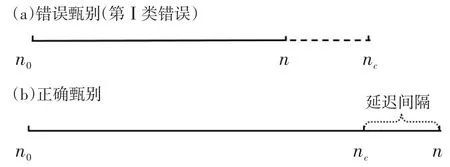
图1 错误与正确的变点甄别
2.2 基于经典测量理论的序贯监控方法
在计算机自适应考试中,每道试题都有潜在的目标考生子群体,这个子群体与总考生群体是不一样的。例如,在计算机自适应考试中,较难的题目是被设计用以考查较高能力考生时使用的。因此,总体上来说,一道难题的目标考生子群体比一道较容易题目的目标考生子群体的能力高。在计算机自适应考试系统中,考生群体、试题的难度参数和选题策略及算法共同决定了这个目标子群体。定义p是来自目标子群体中的某一考生在某一被监控试题上的得分期望值:

Zhang[18]认为试题信息泄露作为变点问题可通过p值反映出来,并据此针对计算机自适应考试系统开发了基于经典测量理论的实时连续监控试题统计特性的序贯监控方法。在施测过程中,被监控中的每一道试题,若其信息没有被泄露,那么相应的考生作答U1,U2,…,Un…,均具有相同的p值。若某题在第nc个考生后被立即泄露,那么前nc个考生的得分的期望值为p,其后考生得分的期望值为p*,这里

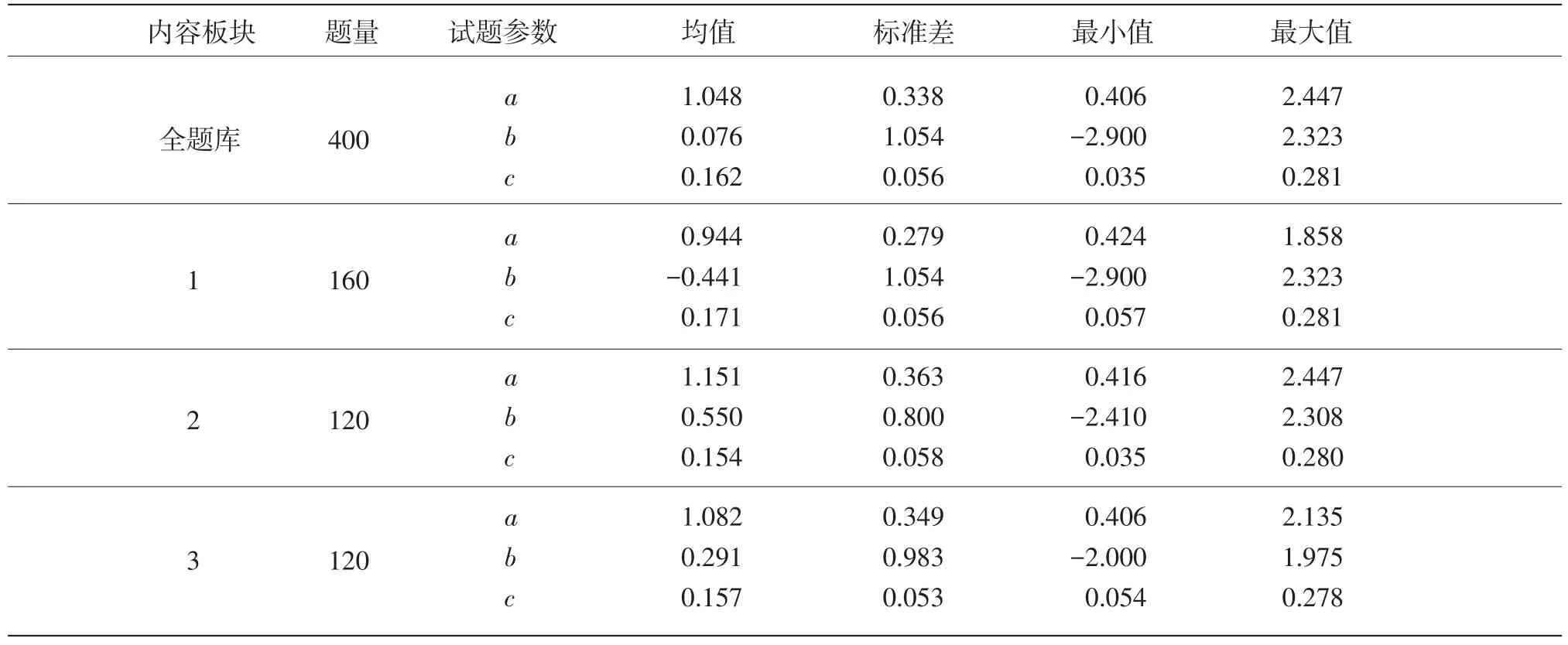
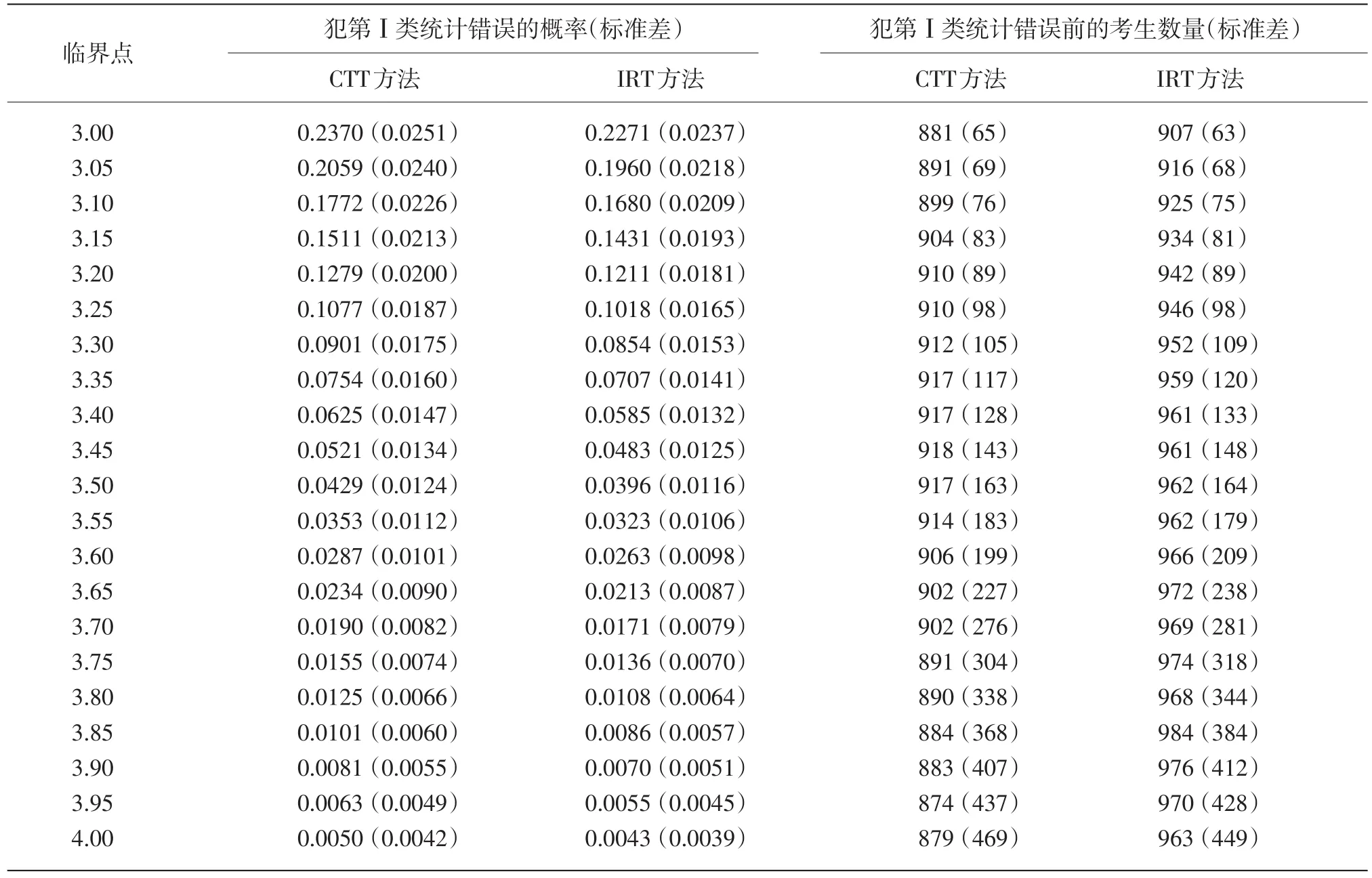
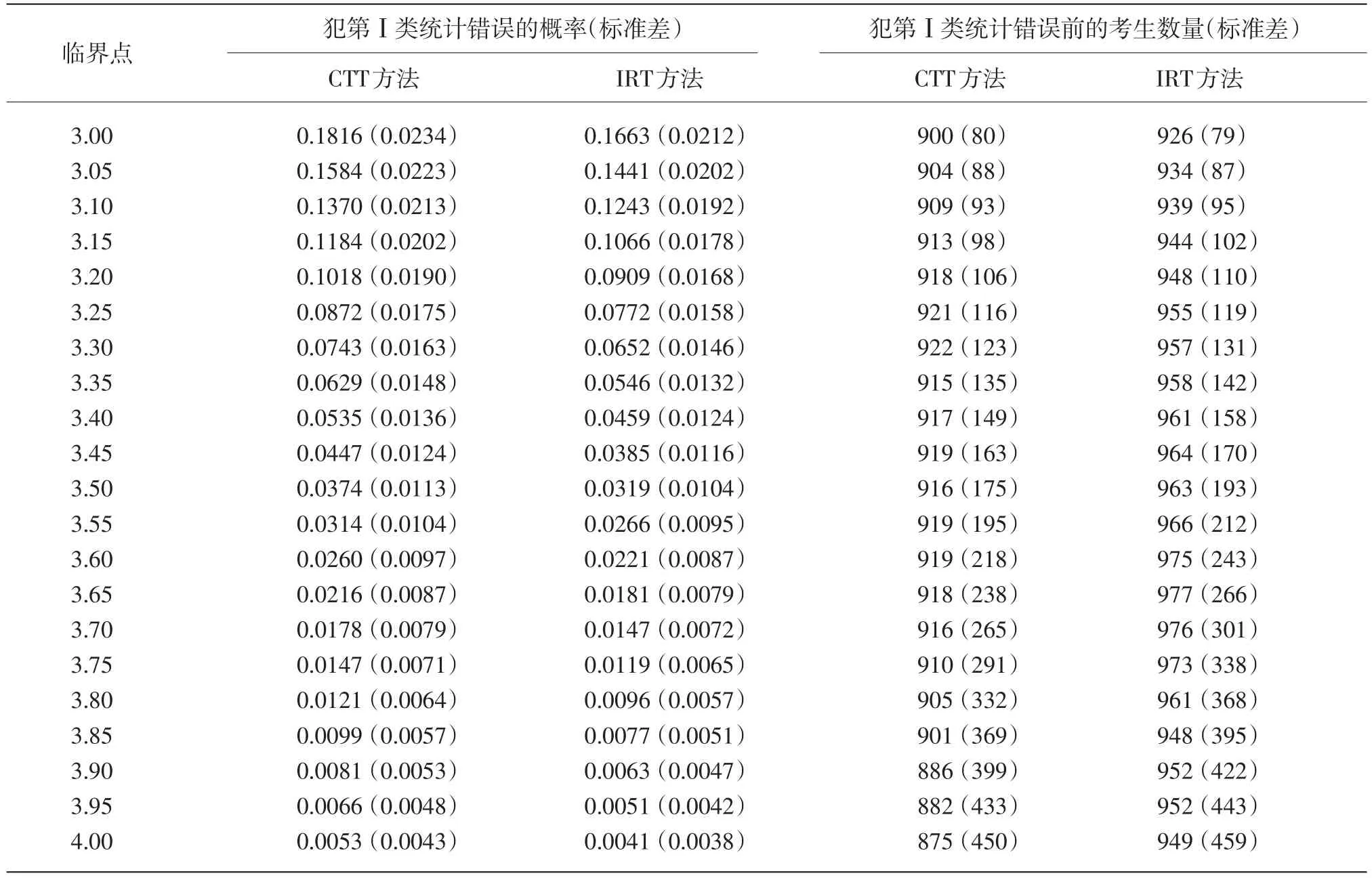
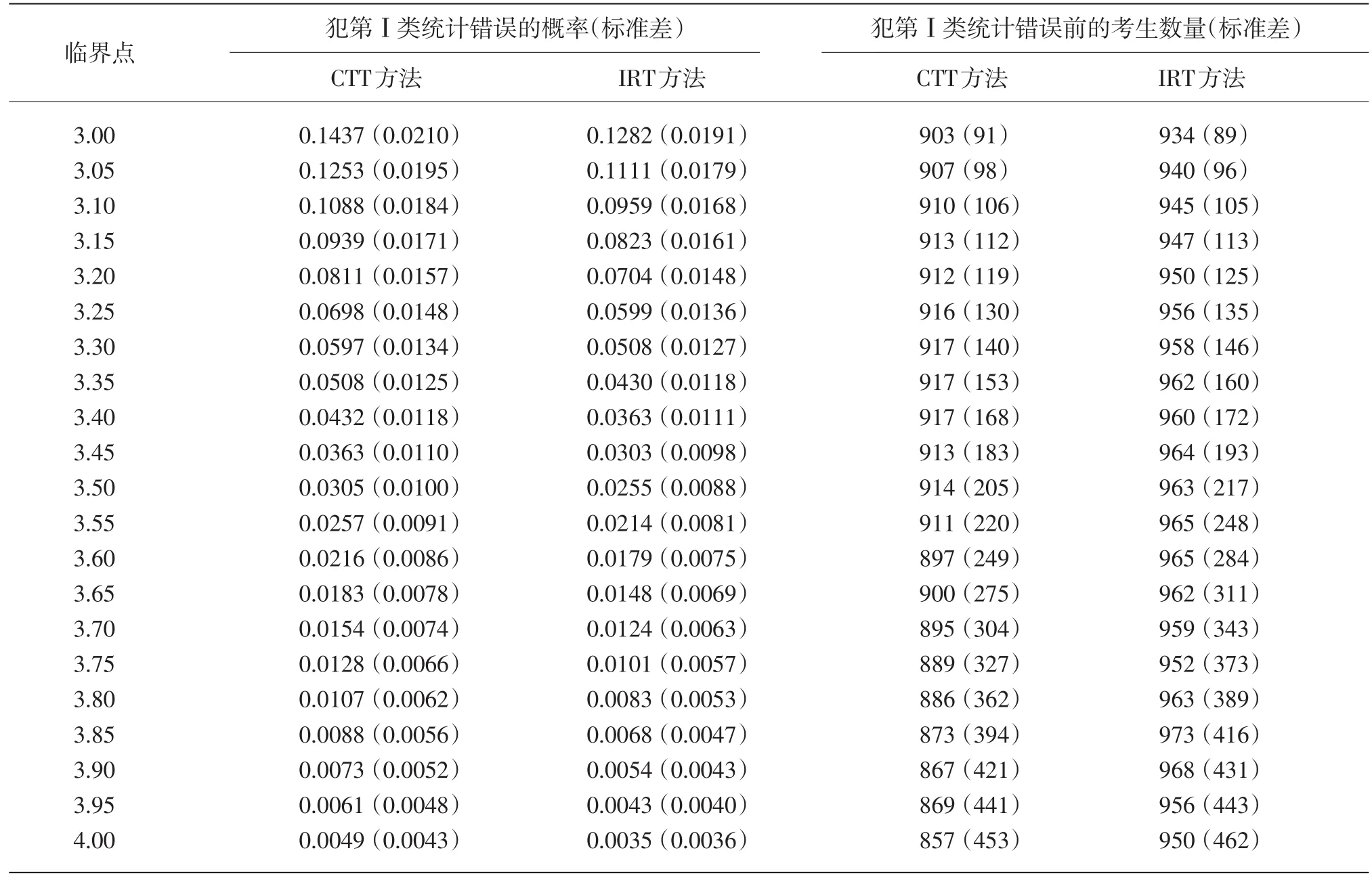
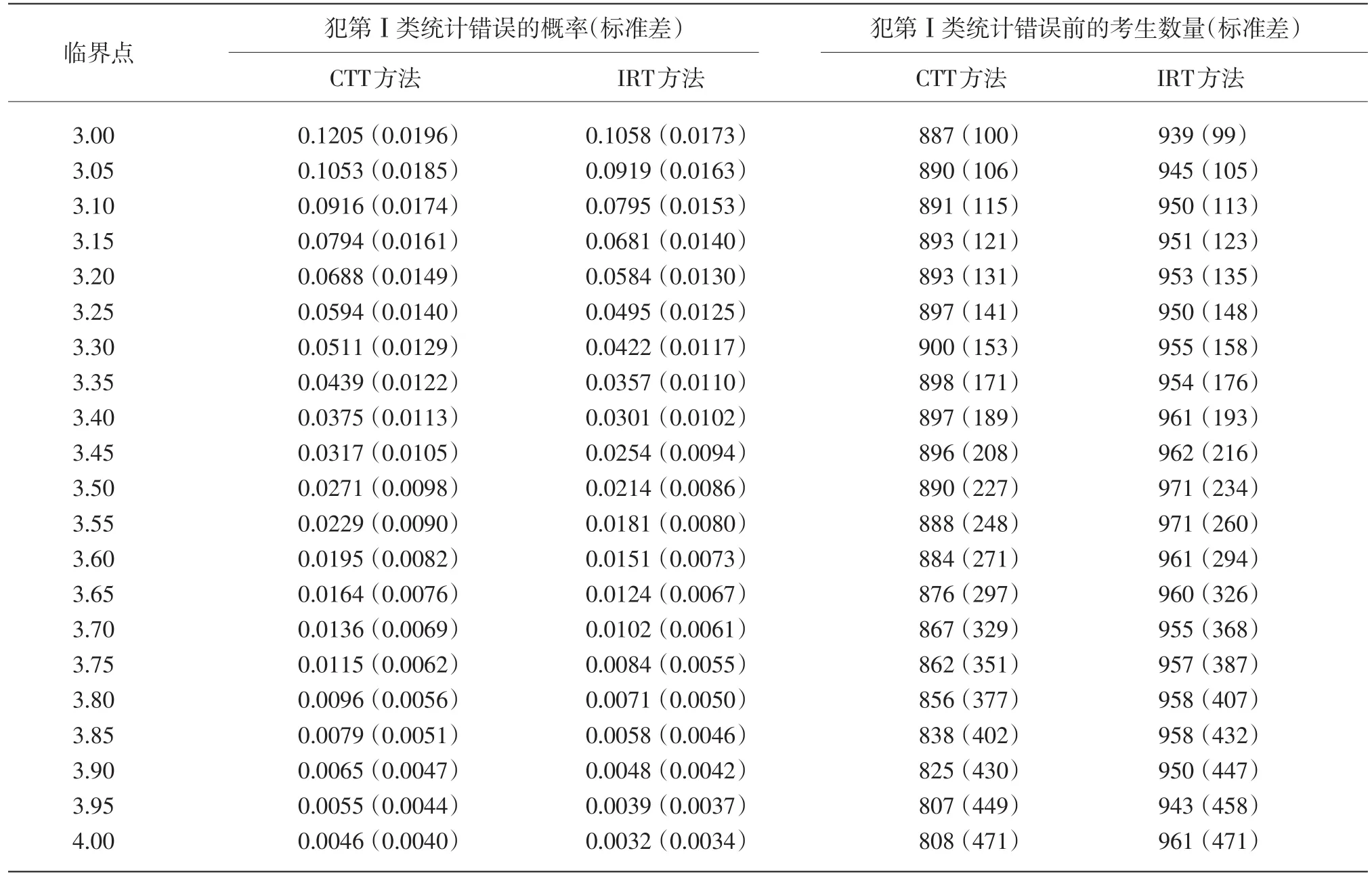
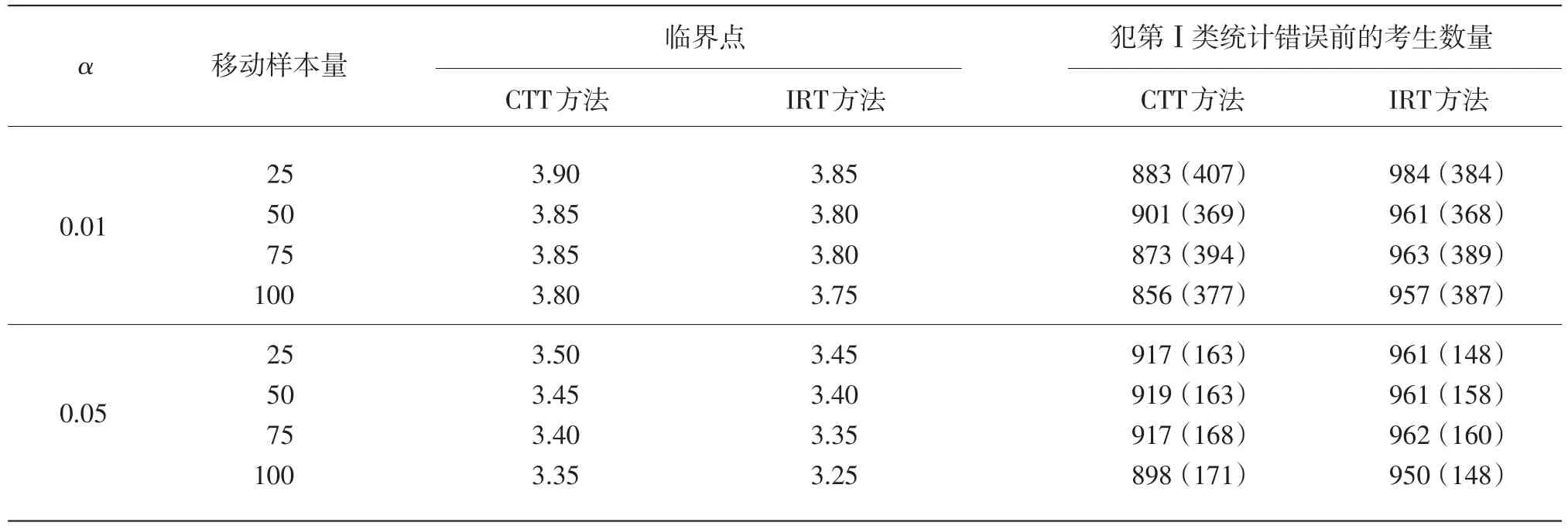
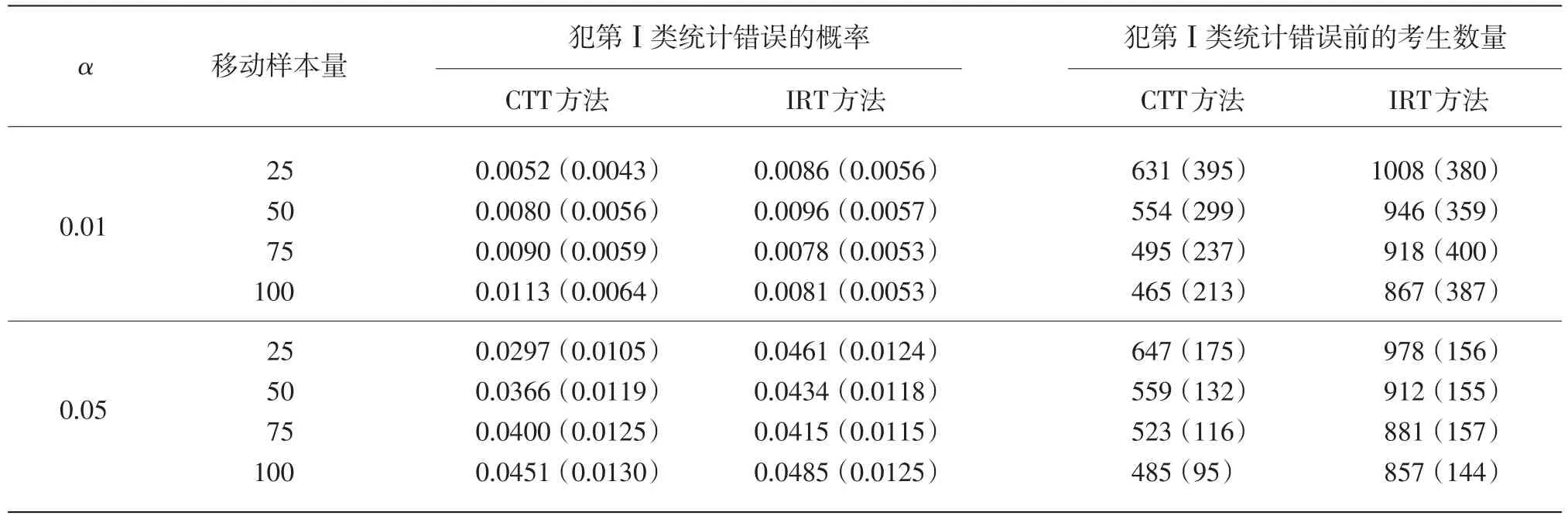
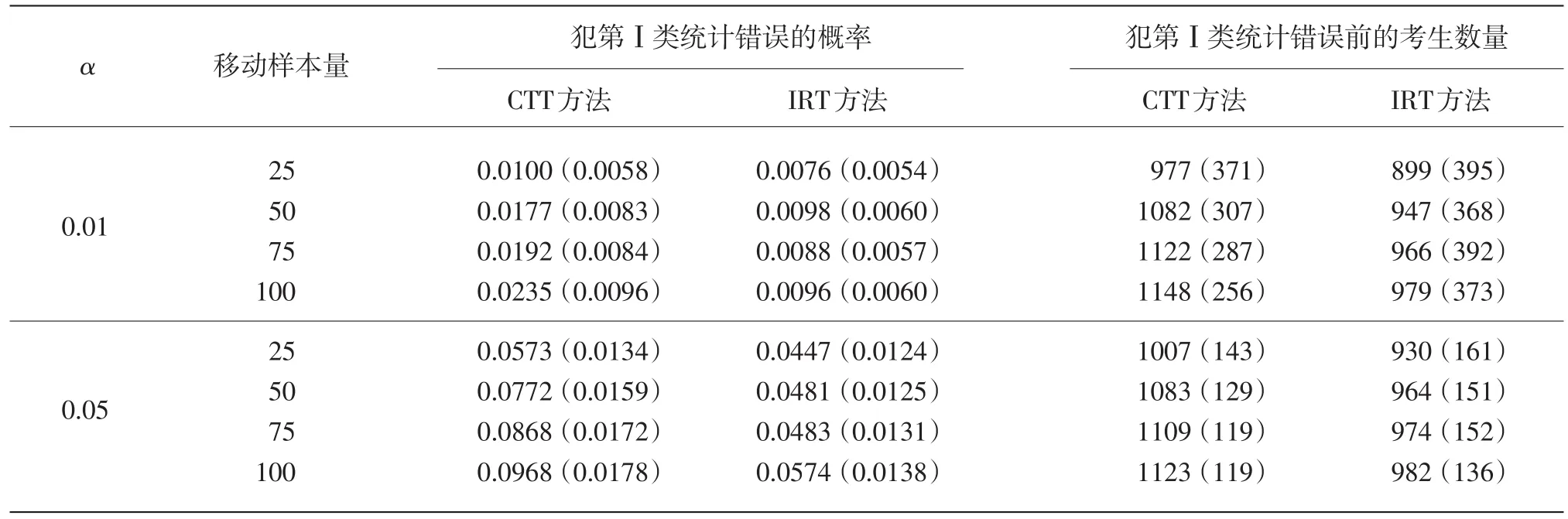
假设当前考生是作答该被监控试题的第n名考生。针对该题的监控过程由一系列统计假设检验构成:至n的原假设为在第n个考生使用该试题时,该试题还未被泄露;相应的备择假设为该试题在第n个考生或其之前就已经被泄露。至n的假设检验将到当前为止的n个考生对该试题的作答分为两个部分:前个考生作答{U1,U2,…,Un-m}被称为至n的参考移动样本,而从考生n-m+1到考生n的m个作答{Un-m+1,Un-m+2,…,Un}被称为至n的目标移动样本。这里“移动”是指在实时连续监控试题的过程中,n是不断向前移动的,而m(m 令 若该试题在第n个考生作答时还没有被泄露,那么和均为p的无偏估计。因此的数值应较小。然而,若该试题在第n个考生作答前就已经被泄露,尤其当nc=n-m时是在该试题被泄露后对正确作答概率的估计,而仍是在该试题被泄露前对正确作答概率()p的估计。由于试题泄露会导致该题变得简单,即p*>p,所以的值也会相应地增大。因此,可以用来构造假设检验的统计量,其被标准化后被记为 至n的假设检验为:如果大于预设的临界值cα,就拒绝至n的原假设,即认为至n时该试题已被泄露。 基于经典测量理论的监控方法的操作过程为:对于题库中的每一道试题,在施测过程中一旦使用该试题的人数达到一定数量(例如,n0=150)时,就开始依据公式(4)计算的数值。如果就可认为该试题已泄露,这里n=n0,n0+1,n0+2,...。即该监控程序由一系列统计假设检验构成,在考试过程中,每当一道受监控试题被选用于当前考生,就重新计算该题的并与预先设定的临界值cα进行比较,做显著性检验。 2.3 基于项目反应理论的序贯监控方法 由于计算机自适应考试一般均建立在项目反应理论的基础之上,然而前述所介绍的基于经典测量理论的序贯监控方法并没有直接运用项目反应理论中的任何主要成分,例如能力估计和项目反应函数。如果项目反应理论中的主要成分和统计量能被加以利用,就有可能开发出更为理想的监控程序。在这一点的启发下,Zhang&Li[19]开发了基于项目反应理论的实时连续监控方法。 若该试题在n-m处或之前已被泄露,则Xnm是试题泄露后的正确作答观测值,其期望值为 基于项目反应理论的序贯监控方法的操作过程为:对于题库中的每一道试题,在施测过程中一旦使用该试题的人数达到一定数量(例如,n0=150)时,就开始依据公式(5)计算的数值。如果就可认为该试题已泄露,这里n=n0,n0+1,n0+2,...。即该监控程序由一系列统计假设检验构成,在考试过程中,每当一道受监控试题被选用于当前考生,就重新计算该题的并与预先设定的临界值cα比较,做显著性检验。 基于经典测量理论的序贯监控方法是通过比较基于目标移动样本与参照移动样本p值的估计来实现对试题统计特性的实时连续监控,而基于项目反应理论的监控方法则只需要使用目标移动样本。上述两种序贯监控方法都含有参数cα和m,其均需要在相应的序贯监控方法被应用于具体的计算机自适应考试系统之前被确定下来。这两个参数,特别是临界值cα,在上述两种序贯监控程序中往往是不一样的。通常我们希望将犯第Ⅰ类统计错误的概率控制在一定的显著性水平之下。显著性水平α通常被选定为0.01或0.05。当给定显著性水平α后,对各个监控程序,临界值cα就可以通过模拟研究被确定下来。在下文中我们将示范如何用模拟实验来确定临界值cα。在选取目标移动样本大小m时,应注意平衡相应序贯监控方法犯第Ⅱ类统计错误的概率与相应侦测被泄露试题监控过程中的延迟间隔[18]。在其他参数不变的情况下,越大的目标移动样本,即m值越大,相应的序贯监控程序犯第Ⅱ类统计错误的概率越小,但延迟间隔也可能会越大。因此,为获得较小的延迟间隔,不可选取过大的m值。在为序贯监控方法选取最优参数时,应该综合考量众多因素以平衡犯第Ⅰ类错误、第Ⅱ类统计错误的概率以及延迟间隔。那些应该考量的因素包括(但不限于):犯第Ⅰ类统计错误所可能耗费的成本,以及使用已被泄露试题可能会对本次计算机自适应考试评估所产生的破坏。整个过程要依据考试的具体情况来确定。 本研究用模拟计算机自适应考试数据对上述这两种序贯监控方法进行统计稳健性比较。具体地说,首先在考生整体水平随时间没有任何变化的情况下,用模拟实验来确定显著性水平α为0.01和0.05的临界值cα。然后再模拟考生整体水平有季节性变化或连续提高趋势的情况下,检查这两种监控方法犯第Ⅰ类统计错误的概率是否变大,是否超出预设的显著性水平。本研究既要比较这两种方法在不同情形下的表现,也要比较各个方法从考生整体水平随时间没有任何变化到有变化时的表现。除了犯第Ⅰ类统计错误的概率,即某一题没有被泄露,却被误判为已被泄露的概率,这一概率越小越好外,另一个比较的标准是第Ⅰ类统计错误的发生位置,用犯第Ⅰ类统计错误前的考生数量这一指标来衡量,即犯第Ⅰ类统计错误发生得越晚,在该错误发生前,使用该题的考生数量将会越大,试题越不会被浪费,故而这一指标越大越好。对于这两个标准,一般先考察犯第Ⅰ类统计错误的概率是否超出预设的显著性水平,这是本研究评估稳健性的主要标准;在犯第Ⅰ类统计错误概率得到控制的前题下,再来比较第Ⅰ类统计错误发生的位置,这将作为比较的辅助标准。 3.1 CAT模拟实验设计 此次模拟研究的题库选自一次真实大规模测评的400道试题,这些题目被标定使用三参数Logistic模型: 其中θ表示相应被试者的能力值表示当能力值为θ时正确作答某题目的概率,a表示题目的区分度参数,b表示题目的难度参数,c表示题目的猜测参数[28]。 表1 全题库及各内容板块试题三参数的描述性统计量 测试包含三个内容板块,每个板块分别占总试题的40%、30%、30%,即每个板块分别包含试题160道、120道、120道。表1罗列了全卷及各内容板块相应试题三参数的描述性统计量。 此次模拟研究中,计算机自适应考试试题长度固定为40题,同时对整个选题过程实现内容控制,这样三个内容板块分别包含的题量为16道、12道、12道。对于每个考生或每次考试,每个内容板块试题的出现顺序是通过随机的方式预先设定的:分别使用数字1、2、3来代表三个内容板块,在实验中使用16个1、12个2、12个3,分别通过随机重新排列这些数字以获得考试中试题内容板块的出现顺序,例如,第k个数字是1,那么被选取的第k题则来自第一个内容板块。 给定一个考生真实能力值和一道试题,通过标准IRT方法,使用其相应的真实能力值以及试题参数来产生模拟分数(1或0):从(0,1)均匀分布中产生的一个随机数,如果该数小于基于三参数Logistic模型计算所得的正确作答的概率,那么相应模拟分数被赋值为1,否则为0。 模拟考生的人数为10 000人。对于每一个考生,前三道试题从预先设定的内容板块中曝光率较低的试题中选出,曝光率越低越会被选中。此后的选题方法是结合了内容控制和曝光控制的最大信息量选题法[27]。在此次模拟研究中,试题曝光率会受到严格控制,当前考生的考题只会在那些曝光率低于最大曝光率并满足限制条件的试题中挑选信息量最大的。试题最大曝光率被限定为0.20。注意当所有试题被等概率使用时,平均试题曝光率为0.10(即40/400)。 在选题过程中,此次模拟研究使用后验期望(EAP)方法[29]来估计考生当前的能力水平,该方法使用标准正态分布作为能力值的先验分布。而考生的最终能力估计是用最大似然估计法(MLE)来得到的。 在此次模拟计算机自适应考试的过程中,一旦一道试题的曝光次数达到150次(即 n0=150)就启动序贯监控程序来监测这一试题。这样,实际被监测的试题数量即为题库中曝光次数大于或等于150次的试题数量。此次模拟研究考虑4个不同的移动样本量,m=25,50,75,100。 在每种模拟条件下,模拟实验将重复1 000次。对于每一次重复模拟,首先将记录下列结果:被监测试题数量,被错误标识为泄露的试题数量(即犯第Ⅰ类统计错误),以及发生错误标识前该题被使用的次数(即犯第Ⅰ类统计错误前的考生数量)。然后计算观测到的犯第Ⅰ类统计错误的概率(即被错误标识试题数量与被监测试题数量的比率)和其相对应的第Ⅰ类统计错误发生前的考生数量均值。犯第Ⅰ类统计错误的概率当然是越小越好,不过人们通常选择合适的临界点来控制犯第Ⅰ类统计错误的概率,而犯第Ⅰ类统计错误前的考生数量当然是越大越好。一道试题被用了200次就被错误标识为泄露与一道试题被用了800次才被错误标识为泄露相比,前者的错误更为严重。 3.2 临界点确定 对于给定的显著性水平α(0.01或0.05),需要在所有原假设都成立(即没有试题泄露)的条件下,通过模拟实验来确定本研究介绍的这两种序贯监控程序相应的临界值cα。这一模拟实验通常在一个标准状况下完成。这里所谓的“标准状况”,具体地说,是在模拟实验中考生真实能力值是从均值为0、标准差为1的标准正态分布中相互独立产生,θn~N(0,1),n=1,2,...,N。这里N是模拟考生的人数,在本研究中N=10 000。在这种标准状况下,考生整体水平没有随时间有任何变化。 具体的做法是:首先在标准状况下,用重复模拟实验来确定本文介绍的这两种序贯监控程序在可能的临界值下犯第Ⅰ类统计错误的概率,从而建立临界值与犯第Ⅰ类统计错误概率对应的表格,最后监控程序使用者根据选定的显著性水平α(例如0.01或0.05)来查取相应的临界值。 基于1 000次的重复模拟,平均被监测试题数量为272道题。像前面指出的那样,这个平均被监测的试题数量即为在这1 000次的重复模拟中,题库里曝光次数大于或等于150次的试题的平均数。 模拟结果表明21个可能的临界数值,3.00, 3.05,…,4.00,相对应的犯第Ⅰ类统计错误的概率的范围已涵盖了通常选用的显著性水平的取值,即0.01和0.05。因此,表2至表5只给出了从3.00到4.00(步长为0.05)的21个可能的临界数值所对应的犯第Ⅰ类统计错误的概率。表2至表5是对应于4个不同移动样本量的模拟实验结果,即在这21个可能的临界点下,这两种序贯监控程序在这1 000次的重复模拟中犯第Ⅰ类统计错误的平均比率和犯第Ⅰ类统计错误前的平均考生数量。从这些表中可以看出,随着临界点取值的升高,犯第Ⅰ类统计错误的概率会持续降低。 下面来说明如何使用表2至表5来选取合适的临界值。假如预设的显著性水平为α=0.01,移动样本量预设为m=25时,据表2查得,当临界点为3.85时,基于CTT方法犯第Ⅰ类错误的概率是0.0101,而当临界点为3.90时,基于CTT方法犯第Ⅰ类错误的概率是0.0081。为了把犯第Ⅰ类错误的概率控制在α=0.01以下,当移动样本量预设为m=25时,为CTT方法选取的临界值应为c0.01(CTT)=3.90。当然,为了得到更精确的临界值,可以建立更为精细的表 格以供查用。监控程序使用者也可以使用插值的方法来选取临界值为c0.01(CTT)=3.86。本文为方便起见只用表中数值。同样,当移动样本量预设为m=25时,选取基于IRT方法的临界值为c0.01(CTT)= 3.85。 表2 在理想状况下,不同临界点相应的犯第Ⅰ类错误的概率均值与犯第Ⅰ类统计错误前的考生数量均值(移动样本量为25) 表3 在理想状况下,不同临界点相应的犯第Ⅰ类错误的概率均值与犯第Ⅰ类统计错误前的考生数量均值(移动样本量为50) 表4 在理想状况下,不同临界点相应的犯第Ⅰ类错误的概率均值与犯第Ⅰ类统计错误前的考生数量均值(移动样本量为75) 表5 在理想状况下,不同临界点相应的犯第Ⅰ类错误的概率均值与犯第Ⅰ类统计错误前的考生数量均值(移动样本量为100) 表6罗列了在不同移动样本量下,当显著性水平预设为α=0.01或0.05时,从表2至表5查找出来的临界值cα以及第Ⅰ类错误发生前使用该题的考生数量均值。换句话说,表6综合了表2至表5中的相关信息,概括了在4个不同移动样本量下,对应于常用的显著性水平的临界点和相应犯第Ⅰ类统计错误前的平均考生数量。 本研究只报告了犯第Ⅰ类统计错误的概率,如希望进一步了解有关犯第Ⅱ类统计错误概率的信息,可以参阅Zhang[18]及Zhang&Li[19]发表的文章。在实际应用中,监控程序使用者需要为不同的监控程序选取最佳的移动样本量。如果仅考虑犯第Ⅰ类统计错误前的考生数量的大小,从表6可以看出,CTT序贯监控方法的最佳移动样本量为m(CTT)= 50,而IRT序贯监控方法的最佳移动样本量为m(IRT)=25。当然,监控程序使用者在选取最佳的移动样本量时还需考虑犯第Ⅱ类统计错误概率,使之最小化。从表6也可以看出,IRT序贯监控方法犯第Ⅰ类统计错误前的考生数量普遍比相应CTT序贯监控方法的大,而这个指标是越大越好。 3.3 两种序贯监控程序的稳健性比较 计算机自适应考试的题库通常会使用较长一段时间,几个月甚至几年。考生的整体水平有可能随时间而变化。例如,3月份考生的整体水平比1月份的高。本研究考虑以下两种考生整体水平随时间而变化的情况。 (1)模拟考生整体水平随时间有季节(周期)性变化:考生真实能力值n=1,2,...,10 000。即考生真实能力均值随n有季节(周期)性变化。例如θ1~N(0.0003,1),θ2500~N(0.5,1),θ5000~N(0,1),θ7500~N(-0.5,1),θ10000~N(0,1)。 (2)模拟考生整体水平随时间有持续提高趋势:考生真实能力值θn~N(0.5n/10000,1),n=1,2,..., 10 000。即考生真实能力均值随n有持续提高的趋势。例如θ1~N(0.0,1),θ2000~N(0.1,1),θ4000~N(0.2,1),θ10000~N(0.5,1)。 给定显著性水平0.01或0.05,序贯监控方法中的临界点是在标准状态(考生整体水平随时间没有变化)下得到的。现在考生整体水平随时间有变化,就需要考察这两种序贯监控方法犯第Ⅰ类统计错误的概率是否变大,是否超出预设的显著性水平。在犯第Ⅰ类统计错误概率得到控制的前提下,再来考察第Ⅰ类统计错误发生的位置是否有变化。换句话说,这一节中的模拟试验是用来研究这两种序贯监控方法的稳健性。 表6 在不同显著性水平下,临界点与相应犯第Ⅰ类统计错误前的考生数量均值(标准差) 表7概括了在考生整体水平有季节性变化的情况下,这两种序贯监控方法使用在标准条件下得到的临界点(参见表6)及在不同移动样本量下,犯第Ⅰ类统计错误的概率均值和犯第Ⅰ类统计错误前的考生数量均值。 在考生整体水平有本研究所模拟的季节性变化时,这两种序贯监控方法犯第Ⅰ类统计错误的概率与相应的预设显著性水平(0.01或0.05)可以通过t-检验进行比较。本研究中t-检验的显著性水平均设为0.05。结果表明,在本研究所考虑的4个不同移动样本量的情况中,这两种序贯监控方法犯第Ⅰ类统计错误的概率都没有显著超出相应的预设显著性水平。但是,通过t-检验比较,在所有考虑的情况中,IRT方法犯第Ⅰ类统计错误前的考生平均数都比CTT方法相应的平均数大。这些结果表明在考生整体水平有季节性变化时,这两种序贯监控方法都能很好地控制犯第Ⅰ类统计错误的概率,而在犯第Ⅰ类统计错误前的考生平均数方面,IRT方法略好于CTT方法。 我们还可以通过t-检验比较各个方法犯第Ⅰ类统计错误前的考生数由考生整体水平没有变化到有季节性变化的前后变化(参见表6和表7)。结果表明CTT方法的该指标数,在所考虑的4个不同移动样本量中,全面显著变差(变小);然而IRT方法的该指标数只有在移动样本量为75或100时显著性变差,而在移动样本量为25时变好。 表8概括出在考生整体水平有连续提高趋势的情况下,这两种序贯监控方法使用在标准条件下得到的临界点及在不同移动样本量下,犯第Ⅰ类统计错误的概率均值和犯第Ⅰ类统计错误前的考生平均数。通过t-检验进行比较,发现在本研究所考虑的4个不同移动样本量的情况中,IRT方法犯第Ⅰ类统计错误的概率都没有显著超出相应的预设显著性水平。但是,除了当移动样本量为25时,CTT方法犯第Ⅰ类统计错误的概率都显著超出相应的预设显著性水平。这些结果表明IRT序贯监控方法能很好地控制犯第Ⅰ类统计错误的概率,而CTT方法却不能在所有4个不同移动样本量的情形中控制好犯第Ⅰ类统计错误的概率。另外,通过t-检验表明,在所有4个不同移动样本量的情形中,IRT方法犯第Ⅰ类统计错误前的考生平均数都比CTT方法相应的平均数大。 我们也可以通过t-检验比较各个方法犯第Ⅰ类统计错误前的考生数由考生整体水平没有变化到有连续提高趋势的前后变化(参见表6和表8)。结果表明CTT方法的该指标数,在所考虑的4个不同移动样本量中,全面显著变好(变大);然而IRT方法的该指标数值有增有减,例如,当移动样本量为25时,该指标数值显著变差(变小),而当移动样本量为100时显著变大。 表7 在有季节性变化情况下,不同显著性水平相应的犯第Ⅰ类统计错误的概率的均值,犯第Ⅰ类统计错误前的考生数量均值及其标准差 本研究对基于CTT和IRT的两种实时序贯监控方法在考生水平变化的情况下进行了统计稳健性的比较。首先,在标准状况下,根据预设的显著性水平,确定这两种监控方法各自统计检验的临界点;然后再模拟考生整体水平有季节性变化或连续提高趋势的情况下,检查这两种监控方法犯第Ⅰ类统计错误的概率是否变大,是否超出预设的显著性水平。 在模拟考生整体水平有季节性变化的情况下,基于经典测量理论的序贯监控方法犯第Ⅰ类统计错误的概率能够被有效地控制在预设的显著性水平之下,然而,犯第Ⅰ类统计错误发生前使用该题的考生数量,较考生整体水平没有任何变化的情况而言,显著下降。因此,在这种情况下,该方法的稳健性表现不够理想。在模拟考生整体水平随时间有持续提高趋势的情况下,该方法犯第Ⅰ类统计错误的概率有所上升,特别当移动样本量大于25时,该方法犯第Ⅰ类统计错误的概率显著地超出了预设的显著性水平。然而,结果也显示,第Ⅰ类统计错误发生前使用该题的考生数量,较考生整体水平没有任何变化的情况而言,有显著上升。 基于项目反应理论的序贯监控方法,在模拟考生整体水平随时间有季节性变化和有持续提高趋势这两种情况下,都表现出了较好的稳健性,即犯第Ⅰ类统计错误的概率被很好地控制在预设的显著性水平之下。评价一个统计检验方法稳健性的最重要的指标是在状况或条件发生变化时,该方法犯第Ⅰ类统计错误的概率能否被很好地控制在预设的显著性水平之下。在这一标准下,基于项目反应理论的序贯监控方法比基于经典测量理论的方法表现得更为稳健。 至于另一个指标,第Ⅰ类统计错误发生前使用该题的考生数量,在模拟考生整体水平有季节性变化的情况下,基于经典测量理论的序贯监控方法显著低于基于项目反应理论的方法;而在模拟考生整体水平随时间有持续提高趋势的情况下,基于经典测量理论的方法显著高于基于项目反应理论的方法。 总之,基于项目反应理论的序贯监控方法对本研究所模拟的非标准状况均表现出了较强的适应性及优良的稳健性,而基于经典测量理论的序贯监控方法会在不同程度上受到影响,监测效果相较于考生整体水平没有任何变化的情况而言,有所下降。因此,在本研究所模拟的非标准状况下,基于项目反应理论的序贯监控方法的稳健性表现优于基于经典测量理论的序贯监控方法。 表8 在考生整体水平有连续提高趋势的情况下,不同显著性水平相应的犯第Ⅰ类统计错误的概率的均值,犯第Ⅰ类统计错误前的考生数量均值及其标准差 项目参数标定的准确性是确保计算机自适应考试系统成功的必要条件。在本项研究中,假定这一条件已满足,但在实际的自适应考试过程中,项目参数可能会出现漂移,这时基于项目反应理论的序贯监控方法就需要作出相应的调整。 [1]漆书青,戴海崎,丁树良.现代教育与心理测量学原理[M].北京:高等教育出版社,2002. [2]CHANG H,ZHANG J.Hypergeometric family and test overlap rates in computerized adaptive testing[J].Psychometrika,2002(67):387-398. [3]CHANG H,ZHANG J.Assessing CAT security breaches by the item pooling index[C]//Paper presented at the Annual Meeting of Nation⁃al Council on Measurement in Education.Chicago,IL,2003. [4]DAVEY T,NERING N.Controlling item exposure and maintaining item security[M]//MILLS C N,POTENZA M T,FREMER J J, WARD W C.Computer-based testing:Building the foundation for future assessments.Mahwah,NJ:Lawrence Erlbaum,2002:165-191. [5]GUO J,TAY L,DRASGOW F.Conspiracies and test compromise: An evaluation of the resistance of test systems to small-scale cheat⁃ing[J].International Journal of Testing,2009(9):283-309. [6]MCLEOD L,LEWIS C,THISSEN D.A Bayesian method for the de⁃tection of item preknowledge in computerized adaptive testing[J]. Applied Psychological Measurement,2003(27):121-137. [7]WAY W D.Protecting the integrity of computerized testing item pools[J].Educational Measurement:Issues and Practice,1998(Win⁃ter):17-27. [8]YI Q,ZHANG J,CHANG H.Severity of organized item theft in com⁃puterized adaptive testing:A simulation study[J].Applied Psycholog⁃ical Measurement,2008(32):543-558. [9]ZHANG J,CHANG H,YI Q.Comparing single-pool and multiplepool designs regarding test security in computerized testing[J].Be⁃havior Research Methods,2012(44):742-752. [10]HETTER R,SYMPSON B.Item exposure control in CAT-ASVAB [M]//SANDS W,WATERS B,McBRIDE J.Computerized adaptive testing:From inquiry to operation.Washington,DC:American Psy⁃chological Association,1997:141-144. [11]MILLS C N,STEFFEN M.The GRE computer adaptive test:Opera⁃tional issues[M]//VAN DER LINDEN W J,GLAS C A W.Compu⁃erized Adaptive Testing:Theory and Practice.The Netherlands: Kluwer Academic Publishers,2000:75-99. [12]STOCKING M L.Three practical issues for modern adaptive testing item pools(ETS RR-94-5)[R].Princeton,NJ:ETS,1994. [13]STOCKING M L,LEWIS C.A new method of controlling item expo⁃sure in computerized adaptive testing(ETS RR-95-25)[R].Prince⁃ton,NJ:ETS,1995. [14]STOCKING M L,LEWIS C.Controlling item exposure conditional on ability in computerized adaptive testing[J].Journal of Education⁃al and Behavioral Statistics,1998(23):57-75. [15]SYMPSON J B,HETTER R D.Controlling item-exposure rates in computerized adaptive testing[C]//Proceedings of the 27th annual meeting of the Military Testing Association.San Diego,CA:Navy Personnel Research and Development Center,1985:973-977. [16]MILLS C N,STOCKING M L.Practical issues in large-scale com⁃puterized adaptive testing[J].Applied Measurement in Education, 1996(9):287-304. [17]CHEN S,ANKENMANN R D,SPRAY J A.The relationship be⁃tween item exposure and test overlap in computerized adaptive test⁃ing[J].Journal of Educational Measurement,2003(40):129-145. [18]ZHANG J.A sequential procedure for detecting compromised items in the item pool of a CAT system[J].Applied Psychological Mea⁃surement,2014(38):87-104.DOI:10.1177/0146621613510062. [19]ZHANG J,LI J.Monitoring Items in Real Time to Enhance CAT Se⁃curity[J].Journal of Educational Measurement,2016,53(2):131-151.DOI:10.1111/jedm.12104. [20]ANSCOMBE F J,GODWIN H J,PLACKETT R L.Methods of de⁃ferred sentencing in testing the fraction defective of a continuous output[J].Supplement to the Journal of the Royal Statistical Soci⁃ety,1947(9):198-217. [21]CARLSTEIN E.Nonparametric change-point estimation[J].Annals of Statistics,1988,16(1):188-197. [22]LORDEN G.Procedures for reacting to a change in distribution[J]. Annals of Mathematical Statistics,1971,42(6):1897-1908. [23]PAGE E S.Continuous inspection schemes[J].Biometrika,1954(41):100-115. [24]POLLAK M.Optimal detection of a change in distribution[J].An⁃nals of Statistics,1985(13):206-227. [25]SIEGMUND D.Sequential Analysis[M].New York,NY:Springer, 1985. [26]SIEGMUND D.Boundary crossing probabilities and statistical ap⁃plications[J].Annals of Statistics,1985,14(2):361-404. [27]LORD F M.Applications of item response theory to practical test⁃ing problems[M].Hillsdale,NJ:Lawrence Erlbaum Associates, 1980. [28]罗照盛.项目反应理论基础[M].北京:北京师范大学出版社, 2012. [29]BOCK R D,MISLEVY R J.Adaptive EAP estimation of ability in a microcomputer environment[J].Applied Psychological Measure⁃ment,1982(6):431-444. Robustness of CTT-and IRT-based Sequential Procedures for Detecting Compromised Items in CAT ZHANG Jinming,CAO Canxi,JIE Yongjing CTT-and IRT-based sequential procedures are introduced for monitoring items in a CAT item pool in order to identify compromised items in real time,remove or replace them with appropriate new items,and ultimately enhance test security and validity.This article focuses on the robustness of these two procedures when the overall ability of test takers increases with time or changes seasonally.Specifically,it investigates whether the rates of type I errors of the two procedures become larger than the corresponding significance level in these two scenarios.Results from simulation studies demonstrate that the IRT-based sequential procedure is more robust than the CTT-based one in the settings specified in the article. Computerized Adaptive Testing;Item Response Theory;Classical Testing Theory;Item Exposure; Change-point Problem;Sequential Method G405 A 1005-8427(2017)02-0020-14 10.19360/j.cnki.11-3303/g4.2017.02.004 (责任编辑:陈睿) 本研究得到中国国家汉语国际推广领导小组办公室提供的部分资助。 张金明(1962—),男,博士,美国伊利诺伊大学香槟分校,副教授;曹灿兮(1990—),女,美国伊利诺伊大学香槟分校,在读研究生;揭勇菁(1991—),男,美国伊利诺伊大学香槟分校,在读研究生。
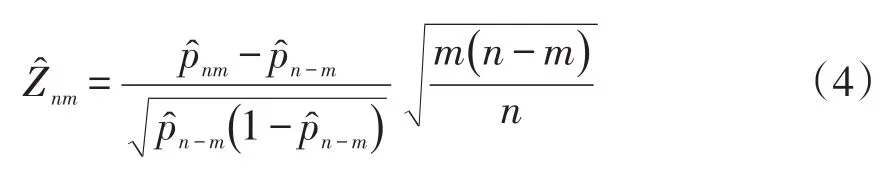
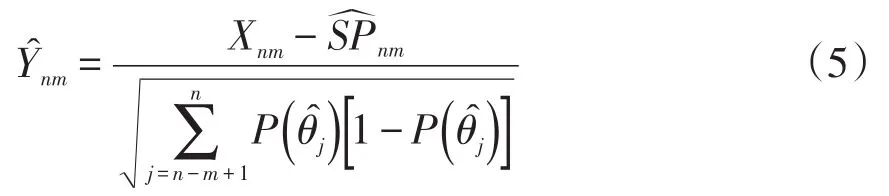
3 模拟研究
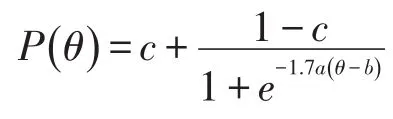
4 讨论
(University of Illinois at Urbana-Champaign,Illinois 61822,US)
