一种惯性测量单元非正交安装的单轴转位方法

张福斌，周振华

（西北工业大学 航海学院，西安 710072）

一种惯性测量单元非正交安装的单轴转位方法

张福斌，周振华

（西北工业大学 航海学院，西安 710072）

针对单轴旋转式捷联惯导系统中旋转轴方向惯性器件误差导致系统误差积累的问题，提出一种惯性测量单元非正交安装的单轴转位方法，该方法不但可消除旋转轴垂直方向惯性器件误差对导航精度的影响，而且可减小旋转轴方向惯性器件误差引起的导航误差。基于单轴旋转调制原理，推导了非正交安装方法和正交安装方法的陀螺常值漂移和加速度计零偏在单轴旋转下引起的姿态误差，并对其进行分析，结果表明，在陀螺仪和加速度计常值漂移及零偏相同的情况下，非正交安装方法与正交安装方法相比，安装斜角为10°时72 h的定位误差降低约50%。

非正交安装；惯性导航；单轴旋转；姿态误差

捷联惯性导航系统中，构成惯性测量单元的陀螺仪和加速度计的误差是捷联惯导系统误差的主要来源[1]，仅从惯性器件制造工艺上提高精度，器件精度越高，进一步提升器件精度的代价就越大，采用惯性组件误差补偿的方法来提高系统的导航精度是一种有效的途径。一般情况下，惯性组件的误差补偿可以分为两种：一种是利用外部信息进行校正，如组合GPS信息[2]、多普勒信息[3]等；一种是惯性组件误差的自补偿方法[4]。

旋转调制技术就是一种误差自补偿的方法，按其旋转轴数目的多少可以分为单轴系统、双轴系统和三轴系统等类型，每一种类型均有不同的转位方法和误差传播特性[5-7]。

在目前公开发表的文献中，单轴旋转惯性测量单元均采用正交的安装方法，它仅能够调制水平惯性器件误差，对于旋转轴方向的惯性器件误差不能有效调制。本文提出一种惯性测量单元非正交安装的单轴转位方法，可减小旋转轴方向上的惯性器件误差，提高整个导航系统的精度。

通过对惯性测量单元正交安装和非正交安装的输出误差分析，阐述采用传统的大于360°两位置持续正反转位下系统误差自动补偿的基本原理，推导在两种安装方式下的误差传播特性，并通过仿真验证。

1 旋转调制基本原理

单轴旋转式捷联惯导系统调制基本原理是利用转动周期内规律变化的姿态矩阵，对陀螺仪和加速度计的误差进行调制，以此抑制导航系统误差的积累，达到提高导航系统精度的目的[8-10]。约定 n系为导航坐标系（东北天），b系为载体坐标系，s系为旋转坐标系。

2 惯性测量单元安装误差分析

2.1 惯性测量单元正交安装误差分析

2.1.1 陀螺常值漂移误差

初始时刻，假定IMU坐标系（s系）、载体坐标系（b系）和导航坐标系（n系）重合。从0时刻开始，载体静止，IMU绕载体系Z轴以ω角速度连续匀速转动[11]，如图1所示。

图1 惯性测量单元正交安装单轴旋转示意图Fig.1 Schematic of single-axis rotation for orthogonal installation of IMU

根据坐标转换关系，可得t时刻由s系到b系的转换矩阵为

一个转动周期内，陀螺常值漂移和加速度计零偏引起的载体姿态角误差在导航坐标系下的表示形式分别为

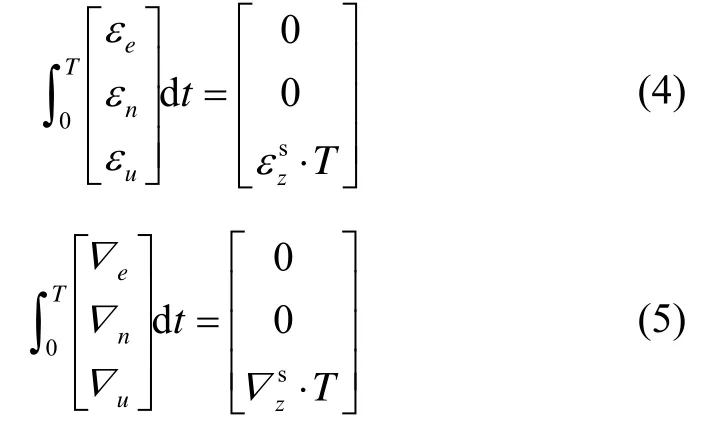
由式(2)～(5)可以看出，系统经过旋转调制，在整周期使等效的东向、北向陀螺常值漂移和加速度计零偏被调制成均值为零的周期函数，长时间来看使系统姿态角误差不再发散，而天向惯性测量单元误差没有被调制，它引起的系统姿态角误差仍按原来的规律传播，成为影响单轴旋转式捷联惯导系统精度的重要因素。

2.1.2 陀螺标度因数误差

初始时刻载体相对地球静止，载体坐标系与导航坐标系重合。转位机构在正向（逆时针）匀速转动过程中，陀螺仪敏感到地球自转角速度和转位机构角速度，其理论输出为

式中，ieω为地球自转角速度，φ为载体所处地球纬度。

由于陀螺标度因数误差的存在，陀螺的输出误差等效到导航系为

其中，Kg为陀螺标度因数矩阵，表达式为

在一个转动周期内，陀螺标度因数误差引起的系统姿态角误差为

由式(9)可知，陀螺标度因数误差不会引起系统东向姿态角误差，然而其标度因数同地球自转角速度耦合，引起北向和天向姿态角误差，长时间看来导致系统姿态角误差发散。

2.2 惯性测量单元非正交安装误差分析

2.2.1 陀螺常值漂移误差

陀螺仪和加速度计分别安装在正三棱锥侧面，过棱锥顶点A的底边垂线的中心位置上，并使惯性测量单元的敏感轴与该垂线平行，OX′Y′Z′为旋转坐标系（s系）。在初始时刻，载体坐标系、导航坐标系与旋转坐标系重合，IMU坐标系与载体坐标系关系如图2所示。

图2 惯性测量单元非正交安装结构图Fig.2 Schematic of IMU with non-orthogonal installation

写成矩阵形式为

其中，

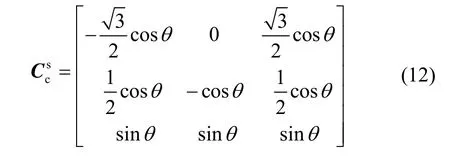
结合式(1)(12)得，t时刻非正交安装结构惯性测量单元误差等效到导航坐标系的惯性测量单元输出误差为

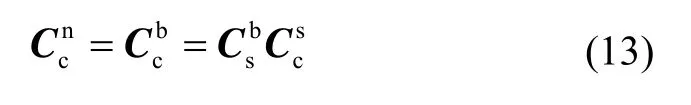
此时，惯性测量单元误差等效到导航系为

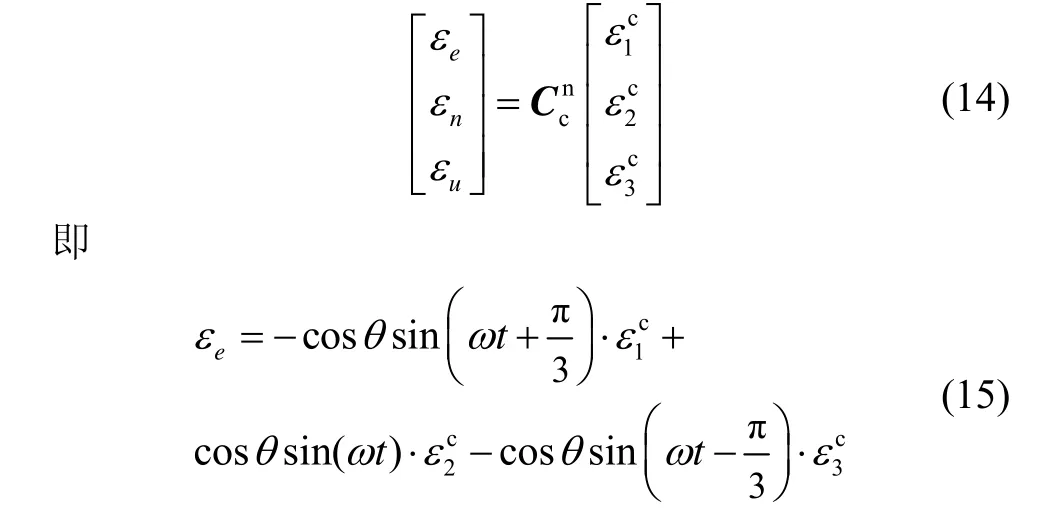
惯性测量单元非正交安装时，一个转动周期内，陀螺常值漂移引起的载体姿态角误差在导航坐标系下的表示形式为

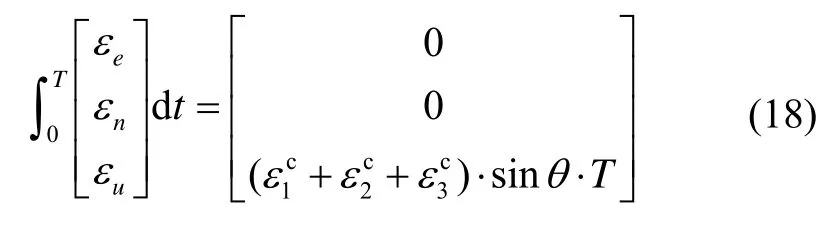
由式(15)～(18)可知：惯性测量单元非正交安装经过旋转调制，转轴垂直方向所在平面上的陀螺常值漂移在导航系的等效误差按正余弦规律变化，在一个旋转调制周期里均值为零，可有效抑制系统姿态角误差发散；天向姿态角误差大小与倾斜角θ角有关，若三个陀螺常值漂移相等，仅考虑陀螺常值漂移的影响，当θ=19.4712°时，导航系统姿态角精度同惯性测量单元正交安装时相当，当θ＜19.4712°时，导航系统姿态角精度优于惯性测量单元正交安装时精度。

2.2.2 陀螺标度因数误差

假设初始时刻载体相对地面静止，此时选定θ为10°，在转位机构正向匀速转动过程中，由于陀螺仪敏感到地球自转角速度和转位机构角速度，其理论输出为

假设陀螺标度因数误差矩阵为Kgc，则由于陀螺标度因数误差引起陀螺输出误差在导航坐标系的投影为

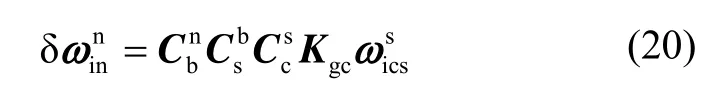
式中，

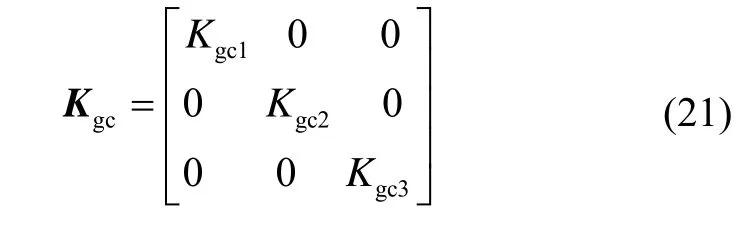
由式(1)(12)(19)～(21)可得，在一个转动周期，忽略计算结果中较小的量，陀螺标度因数误差引起的导航系统姿态角误差为

由式(22)可知，陀螺标度因数误差耦合地球自转角速度引起系统姿态角误差，长期看来导致系统姿态角误差发散。

加速度计误差分析与此类似，这里不再赘述。

3 仿真分析

3.1 仿真条件设置

为了验证惯性测量单元非正交安装单轴旋转的优越性，分别对惯性测量单元正交安装单轴旋转和惯性测量单元非正交安装单轴旋转在陀螺常值漂移、加速度计零偏、陀螺/加速度计标度因数误差下进行了仿真。仿真条件设置如下：

1）载体处于静止状态，载体坐标系与导航坐标系（东北天系）重合，导航位置选为东经108.910°，北纬34.245°。

2）三个陀螺的常值漂移均为 0.01 (°)/h，加速度计零偏选为0.0001g，标度因数误差均为10×10-6，忽略其它误差因素的影响。

3）采用的调制方式是大于 360°两位置单轴持续正反旋转，转位机构角加速度为 2.4 (°)/s2，调制角速度选为 12 (°)/s，惯性测量单元非正交安装单轴旋转时，倾斜角θ选为10°。

4）仿真时间均为72 h。

3.2 仿真结果与分析

图3～6分别给出了惯性测量单元正交安装和惯性测量单元非正交安装下的系统姿态角误差、速度误差和位置误差。

从图3～4可以看出：惯性测量单元正交安装和惯性测量单元非正交安装均不会引起较大的东向和北向姿态角误差；然而，采用惯性测量单元非正交安装单轴旋转方式调制后，经度误差约为原来的一半，纬度存在的地球周期性振荡误差幅值降低为原来的 1/2，经度误差发散趋势明显得到抑制。

图3 导航系统东向姿态角误差和经度误差Fig.3 East attitude error and longitude error of navigation system

图4 导航系统北向姿态角误差和纬度误差Fig.4 North attitude error and latitude error of navigation system

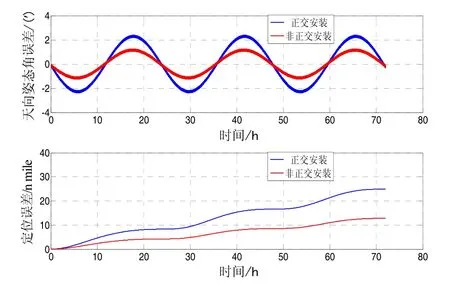
图5 导航系统天向姿态角误差和定位误差Fig.5 Heading attitude error and positioning error of navigation system

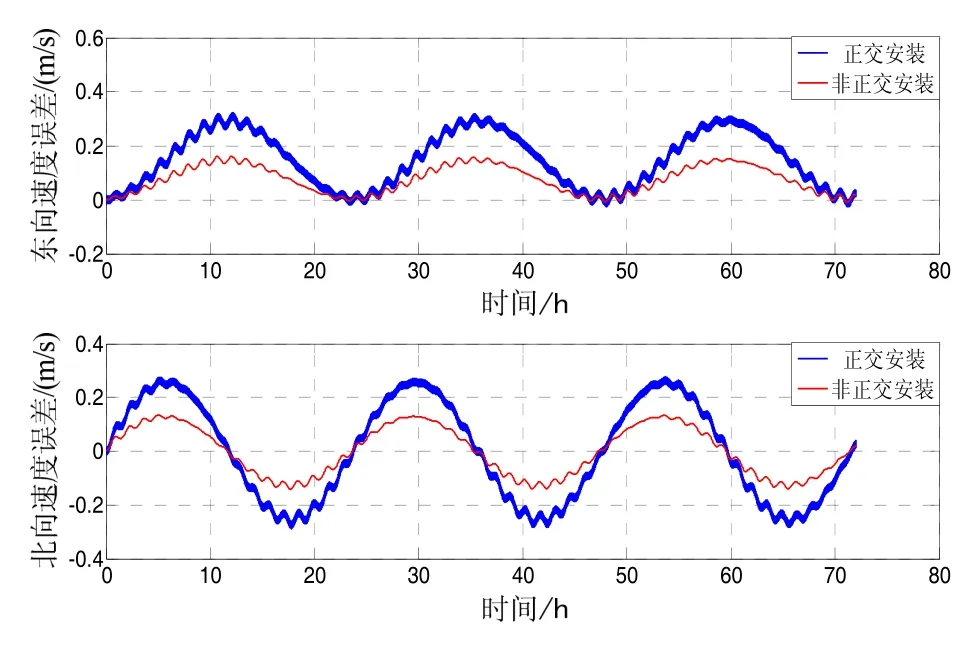
图6 导航系统东向速度误差和北向速度误差Fig.6 East velocity error and heading velocity error of navigation system

从图5～6可以看出：惯性测量单元正交安装单轴旋转条件下，导航系统天向姿态角误差和速度误差相对较大，采用惯性测量单元非正交安装单轴旋转调制方式可提高天向姿态角精度，同时，东向和天向速度误差均减小一半；由于转轴垂直方向的位置误差和姿态角误差均得到一定程度的抑制，因此导航系统的定位精度得到提高，72 h后导航系统定位误差由25 n mile降低到12.8 n mile。

4 结 论

本文推导了惯性测量单元正交安装单轴旋转、惯性测量单元非正交安装单轴旋转误差传播特性，分析了惯性测量单元在两种安装方式下误差调制原理。提出一种惯性测量单元非正交安装的单轴旋转方法，通过选取合适的非正交倾斜角，可有效抑制采用传统单轴旋转方法时方位误差引起的导航系统误差的发散。

（References）：

[1] 魏莉莉, 黄军, 傅长松, 等. 带斜置元件的光纤陀螺捷联惯组标定方法[J]. 中国惯性技术学报, 2015, 23(1): 14-19. Wei Li-li, Huang Jun, Fu Chang-song, et al. Calibration method of FOG strapdown IMU with asked sensor axis[J]. Journal of Chinese Inertial Technology, 2015, 23(1): 14-19.

[2] Zhao L, Gao S, Ding J, et al. Fourier Transforms -Approach to Scientific Principles: Optimized FFT algorithm and its application to fast GPS signal acquisition [M]. InTech, 2011: 157-174.

[3] 李万里. 惯性/多普勒组合导航回溯算法研究[D]. 长沙:国防科学技术大学, 2013. Li Wan-li. INS/DVL integrated navigation by using backtracking scheme[D]. Changsha: National University of Defense Technology, 2013.

[4] Zhang Lun-dong, Lian Jun-xiang, Wu Mei-ping, et al. Research on auto compensation technique of strap-down inertial navigation system[C]//International Asia Conference on Informatics in Control, Automation and Robotics. IEEE Computer Society, 2009: 350-353.

[5] Mao Yu-liang, Chen Jia-bin, Song Chun-lei. Optimal axis selection scheme of SINS single-axis rotation modulation [J]. Journal of Chinese Inertial Technology, 2014, 22(2): 149-156.

[6] Heckman D W, Baretela L M. Improved affordability of high precision submarine inertial navigation by insertion of rapidly developing fiber optic gyro technology[C]// IEEE Position Location and Navigation Symposium. 2000: 404-410.

[7] Benini A, Senatore R, D'Angelo F, et al. A closed-loop procedure for the modeling and tuning of Kalman Filter for FOG INS[C]//IEEE Inertial Sensors and Systems Symposium. Karlsruhe. Germany, 2015: 1-19.

[8] 王庭军. 旋转式捷联惯导系统关键技术研究[D]. 哈尔滨: 哈尔滨工程大学, 2013. Wang Ting-jun. Key technology of rotating strap-down inertial navigation system[D]. Harbin: Harbin Engineering University, 2013.

[9] Sun Feng, Wang Qiu-ying. Researching on the compensation technology of rotating mechanism error in singleaxis rotation strapdown inertial navigation system[C]// International Conference on Mechatronics and Automation. Chengdu, China, 2012: 1767-1772.

[10] Sun Wei, Sun Feng, Wang Da-xue. High precision fiber SINS with spin technology[J]. China Ocean Engineering, 2013, 27(5): 693-702.

[11] Yuan Bao-lun, Han Song-lai, Yang Jian-qiang, et al. Rotation scheme for single-axis index RLG INS[J]. Journal of Chinese Inertial Technology, 2011, 19(2): 145-151.

Single-axis rotation modulation for non-orthogonal installation of IMU

ZHANG Fu-bin, ZHOU Zhen-hua
(College of Marine, Northwestern Polytechnical University, Xi’an 710072, China)

In single-axis strapdown inertial navigation system, the inertial measurement unit (IMU) error along the rotating axis is accumulated with time. To solve this problem, a single-axis rotation modulation method for the non-orthogonal installation of IMU is proposed. By applying the proposed installation method, not only the effect of navigation accuracy due to IMU errors in the orthogonal direction of the rotating axis can be eliminated, but also the navigation error caused by IMU errors in the rotating axis direction can be reduced. Based on the theory of single-axis rotation modulation, the pose errors caused by the constant drift of gyroscope and the zero bias of accelerometer are deduced and analyzed under single-axis rotation by two different methods, namely, the orthogonal rotation and the non-orthogonal rotation. Simulation results show, compared with the orthogonal installation, the 72 h navigation accuracy in case the installation angle is 10° can be improved by 50% under the same conditions of constant drift and zero bias.

non-orthogonal installation; inertial navigation; single-axis rotation; attitude error

V249.32

A

1005-6734(2017)02-0161-05

10.13695/j.cnki.12-1222/o3.2017.02.005

2016-12-18；

2017-03-28

国家自然科学基金（61273333）

张福斌（1972—），男，副教授，从事水下航行器导航与控制研究。E-mail: zhangfb@nwpu.edu.cn