Influences of time synchronization error on angular flexure measurement of ship hull

ZHENG Jia-xing, WU Wei, DAI Dong-kai

(College of Opto-Electronic Science and Engineering, National University of Defense Technology, Changsha 410073, China)

Influences of time synchronization error on angular flexure measurement of ship hull

ZHENG Jia-xing, WU Wei, DAI Dong-kai

(College of Opto-Electronic Science and Engineering, National University of Defense Technology, Changsha 410073, China)

For ship angular flexure measurement based on the ring laser units, the effects of time synchronization error between the two ring laser gyro units are analyzed and evaluated, and an algorithm is proposed to estimate the time synchronization error online. The inertial-frame attitude matching equation considering the time synchronization error is derived, which shows that the time synchronization error will result in extra fluctuation errors of Kalman filter observation as the ship moves in response of the motion of the waves and thus significantly degrade the accuracy of ship angular flexure measurement. In addition, based on the derived inertial-frame attitude matching equation, the delay state is augmented into conventional linear state equations, thus the time synchronization error can be estimated via Kalman filtering. Numerical simulations are carried out with the measured ship attitude data and the angular flexure data of ‘Yuan-Wang Ship’. The simulation results validate the effectiveness of the proposed time-delay estimation method and show that the longer time delay will result in the bigger angular flexure measurement error.

ship angular flexure measurement; time synchronization; ring laser gyro; attitude matching

The attitude of shipboard apparatus (radar antennas, optical systems, etc.), acquired from the central master inertial navigation system, may be corrupted significantly by the existence of ship angular flexure, thereby the ship angular flexure should be measured accurately.

Due to the reliable performance, the ring laser gyro units (LGUs) are attractive for ship angular flexure measurement[6], where the angular rate matching method[1-2]or the attitude matching method[3-5]may be applied to estimate the angular flexure via Kalman filtering. In this paper, based on the newly developed attitude matching method[3], the revised inertial-frame attitude matching equation considering the time synchronization error is strictly derived, from which the influences of time synchronization error between the two LGUs are assessed analytically. Additionally, to reduce the timesynchronization error’s influences on ship angular flexure measurement, an error compensation method is devised based on the delay state augmentation and the revised inertial-frame attitude matching equation. Finally, based on the real measured ship attitude data and angular flexure data of ‘Yuan-Wang Ship’, numerical simulations are carried out to assess the influences of the time synchronization error on ship angular flexure measurement and validate the effectiveness of the proposed time-delay estimation method.

1 Derivation of the revised attitude matching equation

LGU1 and LGU2 are rigidly fixed near the central MINS and any peripheral device, respectively. The angular misalignment (i.e. ship angular flexure) between LGU1 and LGU2 can be estimated via Kalman filtering based on the successive outputs of LGUs.

Equation (2) may be rearranged to give:

This Equation may be rearranged to give:

Rearranging gives:

Assuming that the corresponding Euler rotation angles are small, these DCMs can be approximated as skew symmetric matrices, as follows:

Substituting Equation (10) into Equation (9), rearranging and ignoring product terms, gives:

It can be shown from an element by element comparison that the above equation may be expressed invector form as:

2 T ime-delay estimation model

To reduce the ship angular flexure measurement errors induced by the time-delay, an error compensation method is devised based on the delay state augmentation and the revised inertial-frame attitude matching equation.

The small angular misalignment termis proportional to the angular turn ratessensed by LGU1. Substituting, and writing,and, Equation (12) may be expressed as:

The time delayδmay be modeled as a random constant (actually it’s a slow-varying bias):

Whereek-1,ek′′-1andek′′′-1are assumed to be white noises, andhis the period of Kalman filtering.

Equation (14), Equation (15) and Equation (16) may be combined to form the augmented Kalman filter model as follows:

Where

3 Simulation results

Numerical simulations are carried out to assess the influences of time synchronization error on ship angular flexure measurement and validate the effectiveness of the proposed time-delay estimation method.

3.1 Simulation conditions

Ship motions and angular flexure are both generated based on the real ship data of the ‘YUAN-WANG’ space instrumentation ship in which the attitude data may be acquired from the central main inertial navigation system and the angular flexure is the output of the ‘Optical Deformation Measurement System’. Fig.1 and Fig.2 show 300s-long real measured ship attitude data and the synchronized angular flexure data.

LGU1’s attitude may be simulated by the real attitude data (shown in Fig.1). The angular misalignment between the two LGUs may be simulated by the real angular data (shown in Fig.2) plus a constant angular misalignment (installation misalignment). The installation misalignment is set to 0.1° along each axis. Based on the simulated LGUs’ attitude data, the gyro data outputs may be calculated, and the two LGUs’ gyro bias difference is set to 0.01(°)/h.

Fig.1 Ship attitude

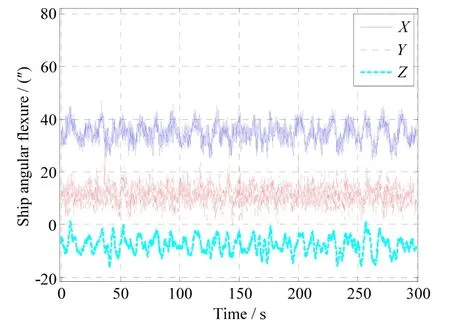
Fig.2 Ship angular flexure

3.2 Effects of the time synchronization error

To strictly assess the influences of the time synchronization error, a group of simulations are carried out where the time delays ranges from -2 ms to 2 ms, as shown in Fig.3. The corresponding root mean square angular flexure estimation errors are illustrated in Fig.4.

Fig.3 Angular flexure errors

Fig.4 Root mean square errors of flexure

From Fig.4, the time synchronization error degrades angular flexure estimation significantly, and the longer time delay may result in the bigger angular flexure error. Additionally, it’s clear that if the time delay is shorter than 0.2 ms, the change of the root mean square flexure error is less than 5″.

3.3 T ime delay estimation

Based on the augmented Kalman filter model provided by Equation (17) and Equation (18), the time delay may be estimated in less than 20 s as illustrated in Fig.5, where the time delay ranges from -10 ms to 10 ms. The corresponding time delay estimation errors are illustrated in Fig.6.

From Fig.6, the time delay estimation error may be less than 0.2 ms, implying that with the time delay compensation, the time synchronization error has little influence on ship angular flexure measurement.

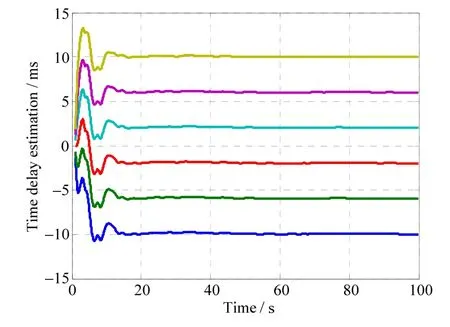
Fig.5 Time-delay estimation results

Fig.6 Time-delay estimation errors

4 Conclusions

The revised inertial-frame attitude matching equation considering the time synchronization error has been strictly derived, from which the influences of the time synchronization error between the two LGUs are assessed analytically. The time synchronization error degrades the angular flexure estimation significantly, and the longer time delay may result in bigger angular flexure error.

To reduce the time synchronization error influences on ship angular flexure measurement, an error compensation method is devised based on the delay state augmentation and the revised inertial-frame attitude matching equation. With the time delay compensation, the time synchronization error has little influence on ship angular flexure measurement.

[1] Mochalov A V, Kazantsev A V. Use of ring laser units for measurement of the moving object deformations[C]// Proceeding of SPIE. 2002, 4680: 85-92.

[2] Schnider A M. Kalman filter formulations for transfer alignment of strapdown inertial units[J]. Navigation, 1983, 30(1): 72-89.

[3] Zheng Jia-xing, Qin Shi-qiao, Wang Xing-shu, et al. Attitude matching method for ship deformation measurement [J]. Journal of Chinese Inertial Technology, 2010, 18(2): 175-180.

[4] Zheng Jia-xing, Qin Shi-qiao, Wang Xing-shu, et al. Ship hull angular deformation measurement taking slow-varying quasi-static component into account[J]. Journal of Chinese Inertial Technology, 2011, 19(1): 6-10.

[5] Yang Yun-tao, Wang Xing-shu, Wu Wei, et al. Optimal estimation of ship angular deformation for autonomous measurement by laser gyro unit[J]. Journal of Chinese Inertial Technology, 2014, 22(3): 284-287.

[6] Day D L, Arruda J. Measuring structural flexure to improve precision tracking[R]. Naval sea systems command, Washington DC, 1999: 1-7.

[7] Zheng Jia-xing, Qin Shi-qiao, Wang Xing-shu, et al. Ship angular flexure measurement considering the slow-varying quasi-static components[C]//18th Saint Petersburg International Conference on Integrated Navigation Systems. 2011: 1-7.

[8] Carlson N A, Kelley R T, Berning S L. Differential inertial filter for dynamic sensor alignment[C]//Proc. Navigating the Earth and Beyond. 1994: 341-351.

[9] Kaiser J, Beck G, Berning S. Vital advanced inertial network[C]//IEEE Position Location & Navigation Symposium. 1998: 61-68.

[10] Kelley R T, Carlson N A, Berning S L. Integrated inertial network[C]//IEEE Position Location & Navigation Symposium. 1994: 439-446.

[11] Joon L, You-Chol L. Transfer alignment considering measurement time delay and ship body flexure[J]. Journal of Mechanical Science and Technology, 2009, 23: 195-203.

[12] Gan Wei-bing, Hu Wen-bin, Zhang Yao, et al. Detection technique for bridge’s micro-deformation based on FOG [J]. Journal of Chinese Inertial Technology, 2016, 24(3): 415-420.

1005-6734(2017)02-0151-05

时间同步误差对船体角形变测量的影响

郑佳兴，吴 伟，戴东凯

（国防科技大学 光电科学与工程学院，长沙 410073）

针对激光陀螺船体角形变测量，分析评估了两组激光陀螺组合体时间同步误差的影响，并提出了一种时间同步误差的在线估计算法。严格推导了考虑了时间同步误差的惯性姿态匹配方程，从方程可见，船体在波浪摇摆条件下时间同步误差将导致额外的 Kalman滤波观测量波动误差，直接影响船体角形变测量精度。另一方面，基于新推导的惯性姿态匹配方程，在滤波状态中增加时间延迟变量，通过Kalman滤波能够在线估计时间延迟大小。基于实测远望船体姿态和角变形数据进行了仿真，仿真测试表明大的时间延迟将导致大的船体角形变测量误差，同时验证了时间延迟在线估计方法的有效性。

船体角形变测量；时间同步；激光陀螺；姿态匹配

U666.1

A

2017-01-16；

2017-03-24

国家自然科学基金（61275002）

郑佳兴（1984—），男，工学博士，讲师，从事惯性技术应用研究。E-mail: 362422833@qq.com

10.13695/j.cnki.12-1222/o3.2017.02.003