基于改进投影寻踪算法的装备保障能力评估

郑显柱， 罗建华， 王树礼， 董玉才， 孙剑桥(． 装甲兵工程学院 科研部， 北京 0007； ． 装甲兵工程学院 兵器工程系， 北京 0007；． 装甲兵工程学院 训练部，北京 0007； ． 装甲兵工程学院 基础部， 北京 0007； ． 装甲兵工程学院 研究生管理大队， 北京 0007)

基于改进投影寻踪算法的装备保障能力评估

针对当前部队装备保障能力评估过程中人为干预引起的误差，深入分析影响装备保障能力的各类要素，构建装备保障能力评估指标体系并进行科学量化，采用改进优化投影寻踪算法对原始装备保障过程中多维数据进行分析，建立装备保障能力综合评估模型，解决了模型中多约束全局寻优的问题。评估实例表明：所提及的算法模型计算效率高、易操作，评估结果客观准确。

装备保障；能力评估；蛙跳算法；投影寻踪模型

装备保障能力建设是部队体系作战能力建设的一个重要组成部分和分支，全面、客观、准确地对部队装备保障能力进行评估,针对装备及其保障系统建设提供合理的改进措施和方法，从而为部队作战、训练提供可靠的装备保障，为首长机关提供决策支撑。而现阶段常用的装备保障能力评估算法中,例如灰色评估法、模糊评估法以及层次分析法等，在评估过程中往往需要专家进行打分或人为确定指标权重，主观因素影响较大，缺乏自适应和自学习能力，容易造成评估结果的随机性和不确定性。因此，建立一套科学完整、行之有效的评估体系和方法对装备保障能力进行科学准确评估，是当前亟待解决的难题。

1 装备保障能力评估概念及指标体系构建

1.1 相关概念及指标体系

当前装备保障能力有多种解释和定义，但总体上可分为2类：

1) 从装备保障内容的角度定义，如，装备保障能力是指为使部队装备保持与恢复作战能力所具备的技术保障、供应保障和调配保障能力[1]；

2) 从装备保障任务的角度定义，如，装备保障能力是指装备保障机构对军队建设、训练、作战和遂行其他军事行动实施装备保障所能达到的程度[2]。

笔者认为，装备保障本质属性是保障性活动，所以，上述关于装备保障能力的2种解释和描述本质上没有区别。基于上述定义，装备保障能力评估就是对装备保障系统完成装备保障任务能力的评价、估量和预测，是装备保障系统内装备管理、装备修理、器材弹药供应保障、设备设施保障、装备保障战备训练、装备保障指挥等因素与特定保障任务的匹配程度和有机结合程度的综合反映。

装备保障能力评估通常需要建立评估指标体系，这也是装备保障能力评估工作的关键。通过对战略、战役、战术各级部队装备保障活动过程和影响装备保障能力的诸多要素分析，可以看出：影响部队装备保障能力的因素分为内部因素和外部因素，所谓内部因素是指与装备保障业务活动相关的要素，外部因素是指装备保障业务活动以外的其他因素(外部因素随着每次作战任务和外部环境的变化而变化，随机性较大，本文不做考虑，仅从装备保障活动本身来展开分析)。内部因素由装备管理、维修保障、器材保障、设备保障、弹药保障、保障人员和保障指挥等7个方面构成，涉及装备保障的“管、修、供、训、战”等相关业务，贯穿于装备保障各项活动。结合近年来对全军部队装备保障基础信息普查、装备保障业务信息系统规划及装备保障能力建设调研情况，遵循完整性、可量化和层次性的评估指标体系建立原则，进一步研究和细化各类保障要素，建立“可量化”和“易量化”的采集指标充分反映影响装备保障能力的影响因素，进而形成装备保障能力评估指标体系。如图1所示，最底层的评估指标都是可进行量化计算的，例如装备管理这个评估要素可通过参评单位保障装备数量、满编率、完好率、配套率以及寿命储备率来进行评估，维修保障可通过参评单位修理机构数量、修理任务完成率和年度修理量来进行评估，器材保障可通过参评单位器材可用数量、紧缺器材数量来衡量，以此类推。

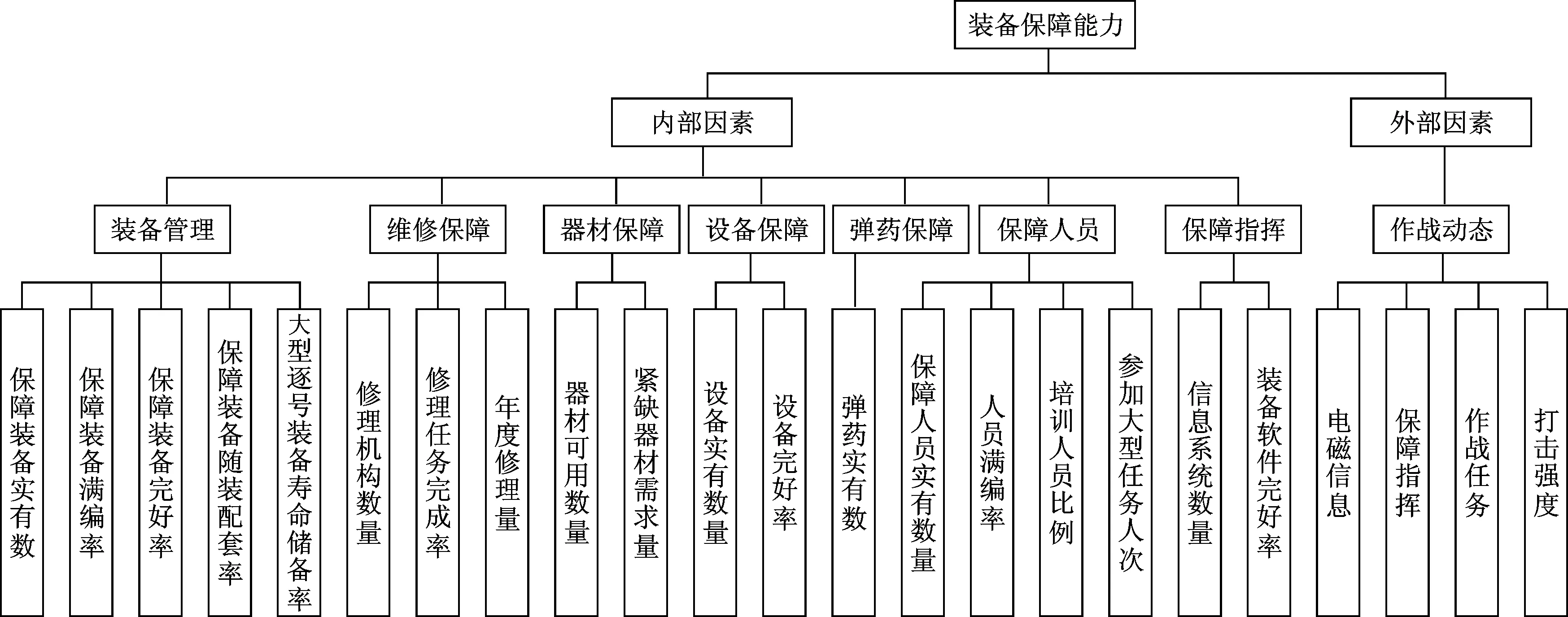
图1 装备保障能力的影响因素和指标

1.2 评估指标量化分析

根据上述对装备保障能力评估指标细化，本节对影响装备保障能力的内部因素进行参数量化分析，量化过程中的数据可从全军装备保障基础信息普查系统、装备保障业务信息系统中获取，尽量减少人为因素的干扰，保持数据的客观真实，为后面模型计算和验证提供支撑。规范和释义如表1所示。

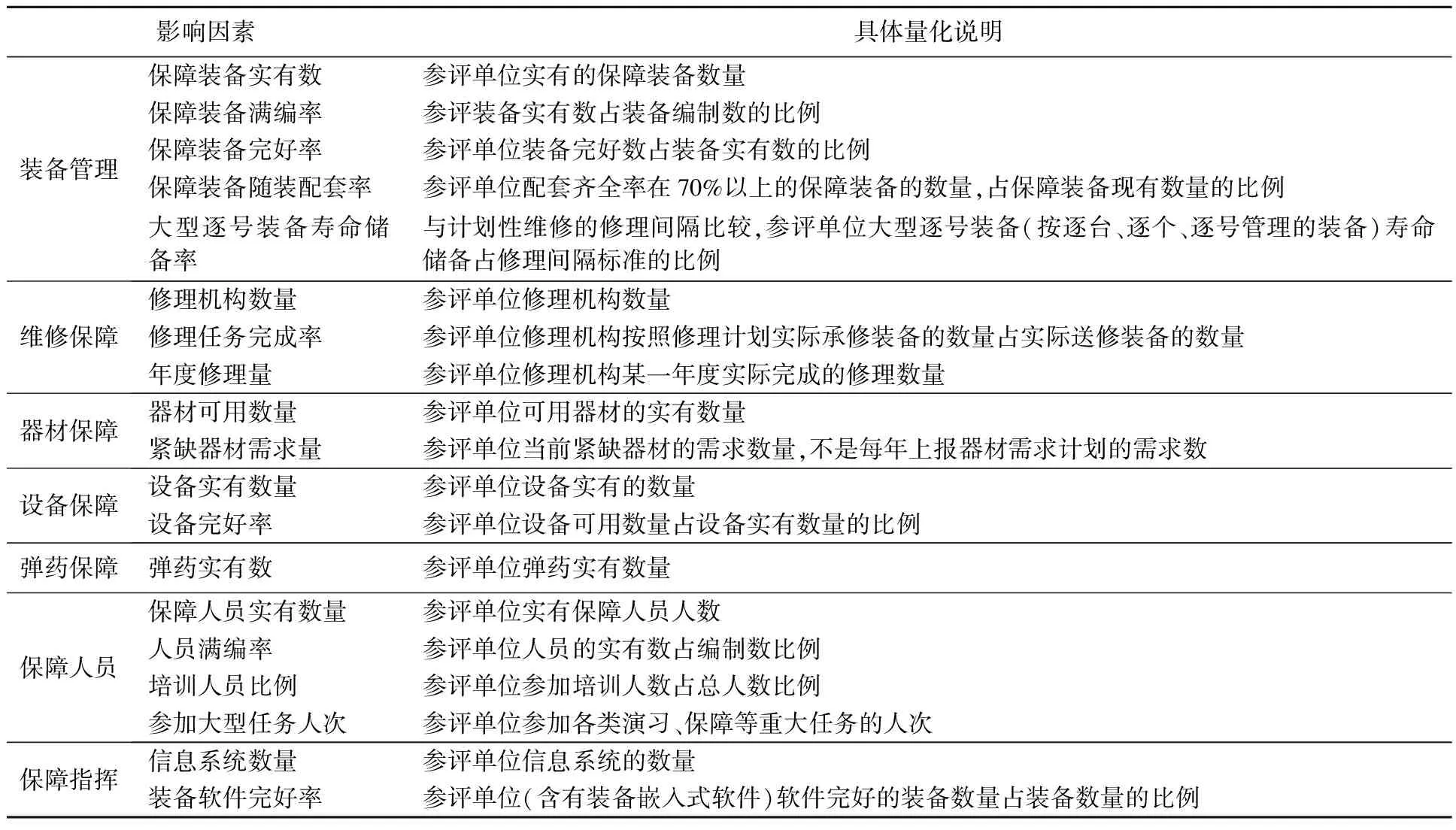
表1 装备保障能力评估指标量化说明

根据上述量化说明和规则，10个指标量化结果可直接通过统计得到，9个指标量化结果需要进行简单计算。需要说明的是大型逐号装备寿命储备率计算的是一个均值，即参评单位所有大型逐号装备寿命储备率的平均值，公式如下：

大型逐号装备寿命储备率=

式中n为大型逐号装备(保障装备)的数量。

2 综合评估算法模型分析

目前，对如何充分利用原始样本数据进行分析，避免人工干预引起的偏差，以及减少人为因素影响的研究还比较缺乏。基于这种考虑，在本文中笔者将蛙跳算法应用于投影指标函数最优化的问题，通过改进投影寻踪算法模型，从而对装备保障能力进行综合评估。

2.1 投影寻踪模型

投影寻踪法是1974年由Friedman和Turkey提出的一种聚类和分类方法[3]，该方法从不同的角度去研究数据，探寻能够最大程度反映待研究数据的特征，并对数据信息进行挖掘，既可作探索性分析，又可作确定性分析。该方法适用于非线性、多变量、非正态等方面问题的研究与分析，得到的评估结果与实际情况结合度高，已经广泛应用于灾情评估、水质评估、企业竞争力评估、工业经济分析等方面的研究中[4-7]。装备保障能力评估属于非线性、多变量、非正态问题，适合该算法模型。

1) 样本评估指标值归一化。样本指标可分为3种类型：越小越好型、越大越好型和区间型。由于各样本指标的量纲和性质各不相同，造成各个指标的不可共度性，需要通过某一效用函数，将不同的指标进行无量纲化处理，并映射到一个有限的区间，称为归一化处理。为了将样本评估指标值转化为闭区间[0,1]上的无量纲指标属性值，采用的计算公式为

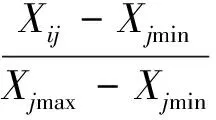
(1)

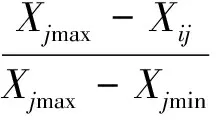
(2)

式中:Xjmin,Xjmax分别为样本集中第j个评估指标的最大值和最小值。对于越大越好型指标，利用式(1)计算；对于越小越好型指标，利用式(2)计算。

2) 构造投影指标函数。设a=(a1,a2,…,am)为单位投影方向向量，将xij进行线性投影，转化为一维投影特征值zi,计算公式为

(3)

式中：i=1,2,…,n;j=1,2,…,m。再根据zi的一维分布图，将样本进行分类。分类原则：样本的局部投影点应该尽量集中，最好的效果是凝聚成若干密集的点团；但在整体上，样本的各个投影点团之间尽可能分散。投影指标函数可用公式表达为

Q=s(a)·d(a)

(4)

式中：s(a)为投影值zi的标准差，称为类间距；d(a)为类密度，表达式分别为

(5)

(6)

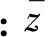
3) 优化投影指标函数。在样本量一定的情况下，投影指标函数Q只跟随投影方向向量a发生变化，最优投影方向a*就是最大可能显示样本某种特征结构的投影方向，因而可以构造投影指标函数最大化问题模型，通过求解模型来估计最佳投影方向，表达式为

maxQ=s(a)·d(a)

(7)

(8)

式(7)、式(8)是一个以aj为变量的多约束优化问题，本文采用蛙跳算法解决该问题，对投影寻踪模型加以改进，提高计算效率。

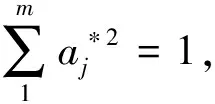
5) 样本投影特征值计算。将优化得到的a*代入到公式：

(9)

即可得投影特征值zi,再根据zi值对各样本进行评估分析。以上计算过程，从样本数据本身出发，没有人工干预

2.2 蛙跳算法

在投影寻踪模型中，投影指标函数最优化问题是m个变量的多约束优化问题，当样本变量较多时，计算量比较大，必须寻找一种合适的方法，对各种投影方向进行计算评估，从而寻找到最佳投影方向，本文拟采用蛙跳算法来解决这个多约束全局寻优的问题。

蛙跳算法是Eusuff和Lansey于2000年模拟青蛙觅食提出的，并于2003年应用于解决最小化问题[8]。该算法结合了粒子群算法和基因进化算法，具有计算速度快、参数少、全局寻优能力强等特点，已得到广泛的应用和验证[9]。

1) 初次分配。设在空间中有P只青蛙构成一个青蛙种群，用第i只青蛙的位置代表该空间的一个解Xi=(xi1,xi2,…,xis),s为维数空间。进行首次分配时，先要计算出每个解的适应值F(Xi),并将P只青蛙按照适应值降序进行排列，而后将整个青蛙种群划分为M个族群(子群)，每个族群中含有N个青蛙。在进行迭代计算过程中，第1个，第2个，…，第M个青蛙依次进入第1,2，…，M个族群;以此类推，第M+1个，M+2个青蛙依次进入到第1个，第2个子群，直到将所有青蛙分配完。

2) 局部搜索。将每个族群中具有最好适应度的解记为Pb,最差适应度的解记为Pw,群体中具有全局最好适应度的解记为Pg。在进行每次迭代计算中，对每个族群的最差适应度Pw的青蛙个体进行更新操作，更新策略为

Dk+1=R*(Pb-Pw)

(10)

(11)

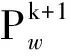
3) 全局信息交换。开展一定次数的局部搜索后，将最初的各个族群青蛙个体进行混合，充分交换青蛙个体之间的信息，按适应值降序重新进行排列和族群划分，而后继续进行上述局部搜索过程，满足收敛条件则停止搜索。

3 评估实例验证

1) 装备保障评估指标体系及样本。应用本文1.2节中对单位装备保障能力评估指标量化分析方法和公式，从全军通用装备保障基础信息普查系统中获取相应的数据，随机取出9个单位的原始数据样本进行指标量化计算，结果如表2所示。

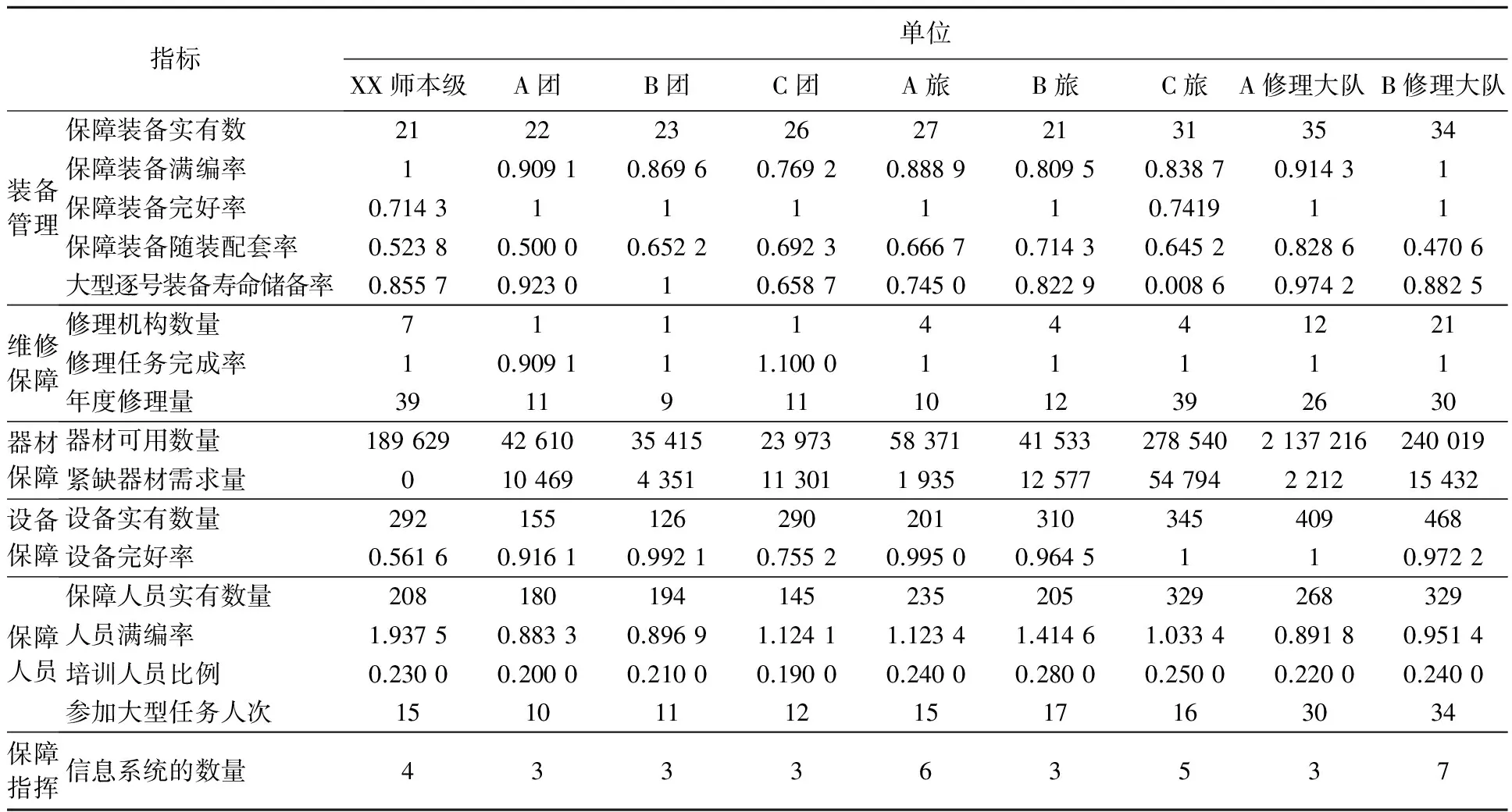
表2 装备保障能力评估指标量化结果

2) 装备保障能力的综合评估。密度阈值取0.1Sz,对装备保障评估样本指标值进行归一化处理，构造投影指标函数，建立投影寻踪模型;利用蛙跳算法，混合迭代次数为500，P=12,M=3，族群内更新次数为4;优化投影指标函数，解决最优化计算中的全局寻优问题，得到各装备保障评估指标的最佳投影方向及权重系数，如表3所示。

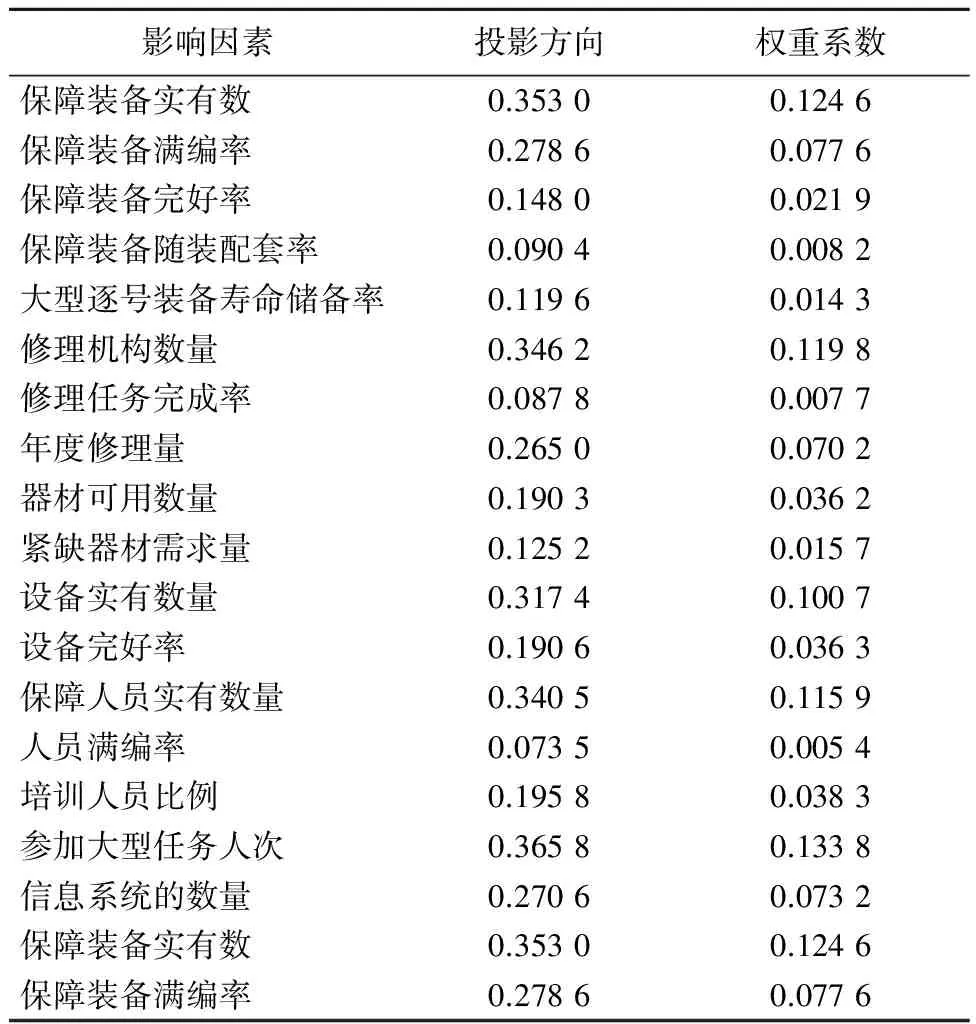
表3 评估指标最佳投影方向及权重系数表

根据式(9)计算得到各单位装备保障能力的投影值，结果及排序如表4所示。

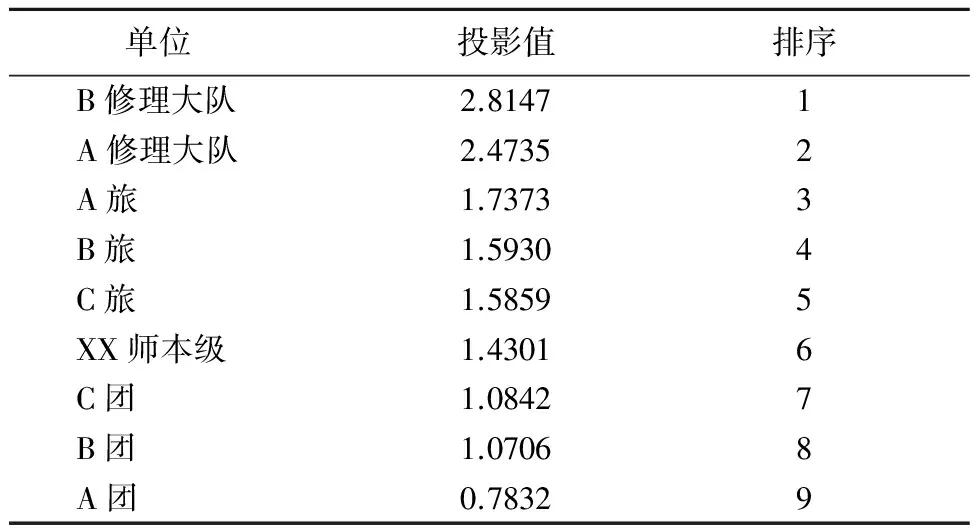
表4 装备保障能力的评估投影值及排序表

通过分析发现：(1) 参评单位中修理大队投影值高于各旅，而各旅高于各团，说明修理大队保障能力明显优于各旅保障能力，而各旅保障能力又明显优于各团保障能力，这与现阶段修理大队、旅、团保障能力的定位是一致的；(2) 参评单位中修理大队、各旅、各团投影值分别在同一档次，说明同一级别、同一类别单位的保障能力的配备处于同一水平，符合实际情况；(3) 可根据本文建立的指标评估体系、模型以及装备保障活动中的各类数据,客观评估各单位的装备保障能力，给出相应的分值和排序。因此，在遂行作战、训练、反恐维稳等一系列军事行动中，可以通过对各单位装备保障能力的综合评估，为指挥员指派、调度、分配任务提供决策依据。

4 结 束 语

装备保障能力评估是装备保障领域的一项重点工作。根据上述思路，将蛙跳算法应用于传统的投影寻踪建模过程中，解决多约束全局寻优问题，避免了专家打分等人为干扰因素，具有较强的客观性、实用性和可操作性。下一步，将重点研究如何在装备保障决策支持系统中嵌入该算法模型，科学高效地对部队装备保障能力进行评估，为首长机关决策提供辅助支持。

)

[1]王汉功，甘茂治．装备全系统全寿命管理[M].北京：国防工业出版社，2003．

[2] 张子丘，王建平．装备技术保障概论[M].北京：军事科学出版社，2001．

[3] FRIEDMAN J H， TUKEY J W.A projection pursuit algorithm for exploratory data analysis[J].IEEE Trans Comput,1974，23(1):881-890.

[4] 胡欣欣.基于投影寻踪的计算机基础实验室绩效评价[J].实验室研究与探索，2013(9)：215-218.

[5] 王会梅，李旭，鲜明，等.网络抗攻击性能的遗传投影寻踪评估模型[J].计算机科学，2010，37(6)：43-45.

[6] 梁彦刚，唐国金，闫野.投影寻踪模型在多属性决策中的应用[J].运筹与管理，2008，17(3)：93-97.

[7] 曹庆璞，董淑福，罗赟骞，等.遗传投影寻踪确定权重的网络仿真评价方法[J].计算机仿真，2010(10)：103-106.

[8] EUSUFF M M，LANSEY K E.Optimization of water distribution network design using shuffled forg leaping algorithm[J].Journal of Water Resources Planning and Management,2003,129(3):210-225.

[9] 郭业才，张苗青.基于混合蛙跳算法的多模盲均衡算法[J].兵工学报，2015，36(7)：1283-1284.

(编辑：李江涛)

Ability Evaluation of the Equipment Support Based on Improved Projection Pursuit Algorithm Model

ZHENG Xianzhu1, LUO Jianhua2, WANG Shuli3, DONG Yucai4, SUN Jianqiao5

(1.Department of Scientific Rearch, Armored Force Engineering, Beijing 100072 , China; 2.Department of Arms Engineering, Armored Force Engineering, Beijing 100072 , China; 3.Department of Training, Armored Force Engineering, Beijing 100072 , China; 4.Department of Basic Course, Armored Force Engineering, Beijing 100072 , China; 5.Department of Graduate Management, Armored Force Engineering, Beijing 100072 , China)

Aiming at the errors caused by the human intervention in the assessment of the current capability of the equipment support in the army, the paper analyzes the various factors influencing the equipment support capability, constructs the evaluation index system of the equipment support capability and scientifically quantifies such capability. The improved and optimized projection pursuit algorithm is used in multi-dimensional data analysis for original equipment support and establishment of comprehensive evaluation on equipment support capacity model so as to solve the problem of multi-constrained global optimization in the model. The evaluation examples show that: the algorithm model mentioned in this paper is computationally efficient and is easy to operate, the evaluation result is objective and accurate.

equipment support; ability evaluation; frog leaping algorithm; projection pursuit model

2016-10-15

部委级资助项目

郑显柱(1982-)，男，助理研究员，博士，主要研究方向为装备保障信息系统工程。zhuzi_zorro@sina.com