基于小生境蝙蝠算法的联合远程打击武器目标分配问题建模与求解
2017-06-05刘双双许瑞明潘俊杰军事科学院军事运筹分析研究所北京00096569部队
刘双双, 许瑞明, 潘俊杰(. 军事科学院 军事运筹分析研究所, 北京 0009; 2. 6569部队)
基于小生境蝙蝠算法的联合远程打击武器目标分配问题建模与求解
刘双双1,2, 许瑞明1, 潘俊杰1
(1. 军事科学院 军事运筹分析研究所, 北京 100091; 2. 61569部队)
针对联合远程打击作战筹划中武器目标分配问题,使用数学建模与仿真分析相结合的方法,研究了联合远程精确打击武器目标分配基本原则,构建了武器目标分配问题的多目标优化数学模型;对目标函数和约束条件进行处理,将该模型转化为单目标优化问题;提出了一种结合小生境淘汰思想的改进蝙蝠算法,用来求解武器目标分配的近似最优解。实验分析表明:该算法能够有效改善蝙蝠算法的收敛特性,适用于联合远程打击作战武器目标分配问题的求解。
武器目标分配;联合远程打击;蝙蝠算法;小生境

联合远程打击作战,是现阶段我军担负的重要使命任务,只有足够重视和强化 “以远制远”的作战能力,才能有效慑止和击溃潜在敌人。在联合远程打击作战筹划中,各军兵种需通过精确规划武器目标分配,确保在有效完成作战任务的前提下,提高武器系统的整体作战效益。武器目标分配(Weapon-target Assignment,WTA)问题的核心,是根据作战目的、作战态势、目标特性和武器性能等因素,把具有不同杀伤力和使用代价的武器,用于打击不同的目标,形成整体优化的分配方案。武器目标分配问题属于NP(Non-deterministic Polynomial,多项式复杂程度的非确定性问题)完全问题[1],该问题的研究主要集中在建模和模型求解算法的设计上。当前,建模研究多是以对目标的毁伤概率最大为目标函数;模型求解主要使用人工免疫算法[2]、粒子群算法[3]、遗传算法[4]98、蚁群算法[5]、模拟退火算法[6]、禁忌搜索算法[7]、NSGA-II[8]等。
蝙蝠算法(Bat Algorithm,BA)由剑桥大学Yang[9]于2010年提出,是一种模拟蝙蝠回声定位捕食原理的启发式群智能搜索算法。蝙蝠算法能以较高概率收敛问题的全局最优解,具有收敛速度快、鲁棒性好的优点[10]。本文将小生境概念引入蝙蝠算法中,研究了小生境蝙蝠算法在武器目标分配中的应用,并通过实例验证了该算法的有效性。
1 联合远程打击武器目标分配建模
1.1 问题描述
文献[11-13]在多种武器攻击多目标的火力分配中,把对目标毁伤概率最大作为优化的目标函数。追求目标毁伤概率最大,可能会导致对某些目标“过度”毁伤,而对另外一些目标打击出现“不足”的情况,从而造成不合理的资源配置。现代战争对于精确火力的运用,更强调使用适当的武器资源达成理想的作战效果,追求整体作战效益最大。可见,该模型已不能很好反映现代战争的制胜机理,与实际作战筹划也不适应。文献[4]98通过设置毁伤阈值,确保对目标的毁伤程度达到预期效果,解决可能出现打击“不足”的问题,但没能解决可能“过度”的问题。
联合远程打击作战中,并非对目标的毁伤越大越好。《日内瓦四公约关于保护非国际性武装冲突受难者的附加协议书》要求控制附带民事损伤,附带损伤可能会使政府陷入政治和舆论上的被动。远程打击作战行动的附带损伤,主要受目标特性、武器精度和火力运用方式等因素影响。在作战筹划阶段,目标特性和武器精度均已确定,但仍可通过合理筹划火力运用以减小附带损伤。文献[14]中的模型通过设置效费比最大准则,虽能使附带损伤受到限制,但仍不能有效控制过度损伤。因此,本文提出附带损伤最小原则,确保在实现打击意图的前提下通过控制火力运用来减少附带损伤。
1.2 武器目标分配原则
武器目标分配问题,要遵循系统的、整体的思想才可能求解出全局最优解。因此,要建立一个适应联合远程打击作战的数学模型,首先要对武器目标分配的基本原则进行分析。一般地,只有对目标的毁伤达到预期效果,才能实现期望的军事效益,如若没有达到预期毁伤效果,作战效能将大打折扣。然而,如果造成附带损伤也会影响作战效益。在以上分析的基础上,建立武器目标分配三原则:
原则1:必要毁伤原则,要求对目标的打击能够满足期望的毁伤概率,确保能够实现指挥员的作战意图。
原则2:附带损伤最小原则,尽量避免出现过度打击,以减小附带损伤带来的政治和舆论影响。
原则3:效费比最大原则,对武器资源进行优化配置,追求武器效能和作战效益的最大化。
1.3 武器目标分配数学建模
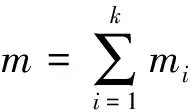
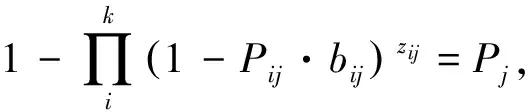
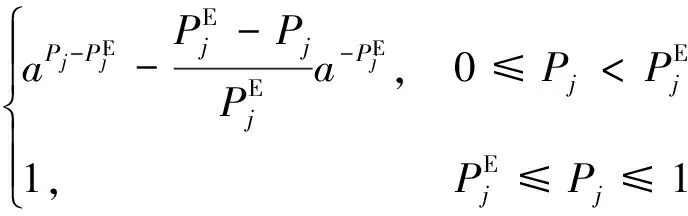
(1)
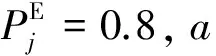
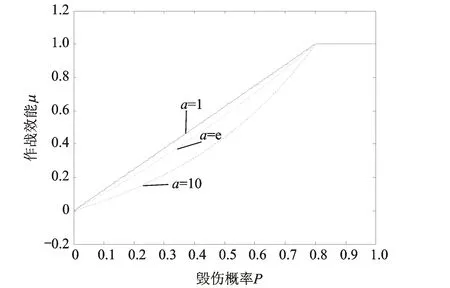
图1 作战效能函数μj曲线示意图
根据“必要毁伤原则”,确保对目标的毁伤达到期望毁伤概率,确定约束条件为
(2)
根据“附带损伤最小原则”,确保尽可能地减小对目标的过度毁伤,构建目标函数为
(3)
联合远程打击作战行动消耗武器资源的总代价为
(4)
联合远程打击毁伤目标带来的总效益为
(5)
根据“效费比最大原则”,确定目标函数为
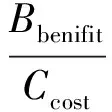
(6)
多种武器打击多个目标问题的优化,要求在确保目标有效毁伤的前提下,使得作战效益最大。该模型求解的输出,是一个或一组能够实现最大效益的分配方案,明确将每一个目标与具体的武器单元建立对应关系。
在既定的战场环境中,相同型号的武器在不同平台上的使用成本和突防概率不同,即便是武器和平台都相同,但配置在不同位置,其突防概率也可能不同。比如,配置在不同海域的同一型号驱逐舰,受战场环境影响,在打击相同目标时的突防概率不同。因此,本文在确定武器种类和数量的时候,与以往仅按型号进行分类不同,即使将型号相同的武器配置在不同的平台或位置也按不同类型武器处理。
2 武器目标分配的小生境蝙蝠算法
2.1 蝙蝠算法
蝙蝠算法中,优化问题的每个解都对应于搜索空间中蝙蝠的位置向量,每个蝙蝠的位置都对应一个由优化问题决定的适应度值。每个蝙蝠通过调整频率、响度、脉冲发射率,追随当前最优蝙蝠在解空间中搜索最优位置[15]。蝙蝠个体是蝙蝠算法的基本单元,蝙蝠群体的运动对应于解空间中的一组解从无序到有序的演化过程。
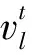
(7)
(8)
(9)
式中:β∈[0,1]为服从标准正态分布的随机变量;x*为d维空间中当前全局最优位置向量;fl为超声波频率。
局部搜索过程中,从当前最优蝙蝠个体中任选一个位置向量xold,那么新的位置向量xnew就在xold附近随机产生,即
xnew=xold+εAt
(10)
式中:ε为一个d维随机向量,向量中所有元素均为[-1,1]上的随机数;At为t时刻蝙蝠群的平均响度。用xnew代替当前位置向量,返回全局搜索继续搜索猎物,避免陷入局部最优。
搜索猎物过程中,最初为了在更广范围搜索,超声波响度A大而脉冲频率r小;发现猎物后,为了进一步精确定位,减小响度A、增大脉冲频率r。响度A和脉冲频率r的更新公式可描述为
(11)
(12)
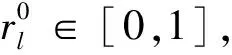
蝙蝠算法的搜索过程分为全局寻优过程和局部寻优过程。其中,公式(7)~(9)用来搜索全局最优位置向量;公式(10)~(12)用来搜索局部最优位置向量。利用蝙蝠算法特有的回波定位特性来避免搜索过程陷入局部最优,是其他智能算法不具有的,使得蝙蝠算法具有其他智能算法不可比拟的优势[16]。
2.2 小生境淘汰机制
生物学中,小生境是指特定的生存环境。生物进化过程中,一般总是与自己相同的物种生活在一起,这就是小生境自然现象。小生境遗传算法(NicheGeneticAlgorithm)是在经典遗传算法的基础上引入小生境技术,基本思想是在经典遗传算法每产生新一代种群时,通过排挤、预选择、适应度共享或者淘汰相似结构等机制使个体能够在解空间中分散开来,更好地维持种群的多样性,从而有效改善经典遗传算法易陷入局部最优解的问题[17]。
基于淘汰相似结构机制的小生境,是通过引入惩罚函数调整个体的适应度值来实现的。淘汰结构相似的个体,使得个体之间存在一定的距离,从而就造成一种小生境的进化环境,维护了种群的多样性,提高了全局搜索能力[18]。本文借鉴了小生境淘汰思想,并将该淘汰机制应用到蝙蝠算法中,以提高蝙蝠算法的全局搜索能力。
2.3 小生境蝙蝠算法设计
为求解联合远程打击作战中武器目标分配问题,设计了小生境蝙蝠算法。以下对该算法的主要操作步骤进行阐述,并给出算法流程。
2.3.1 编 码
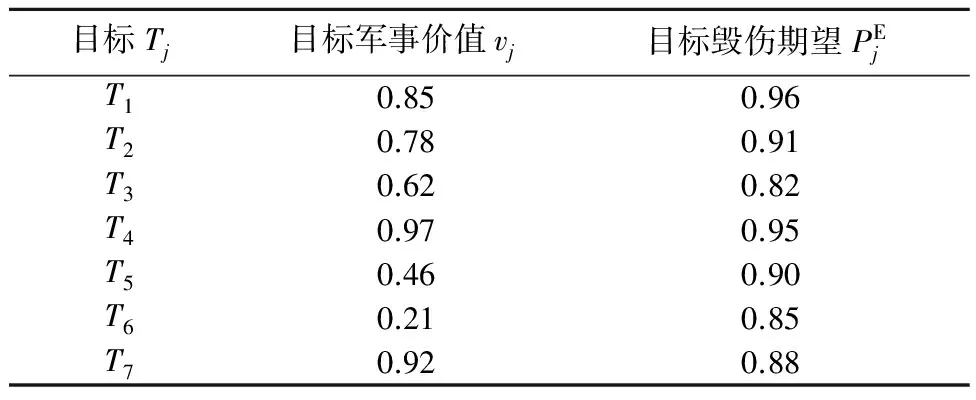
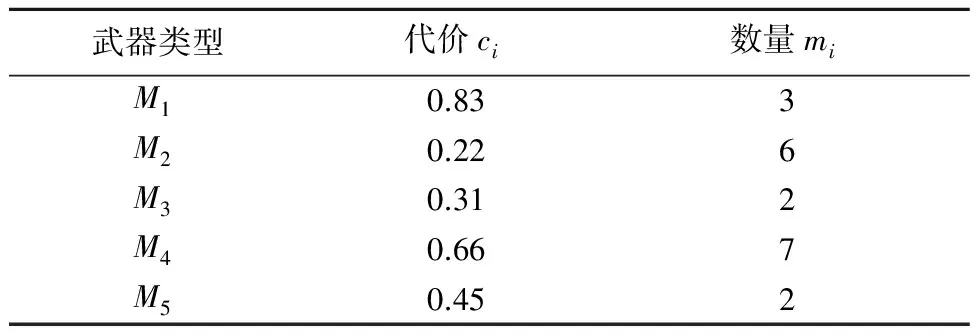
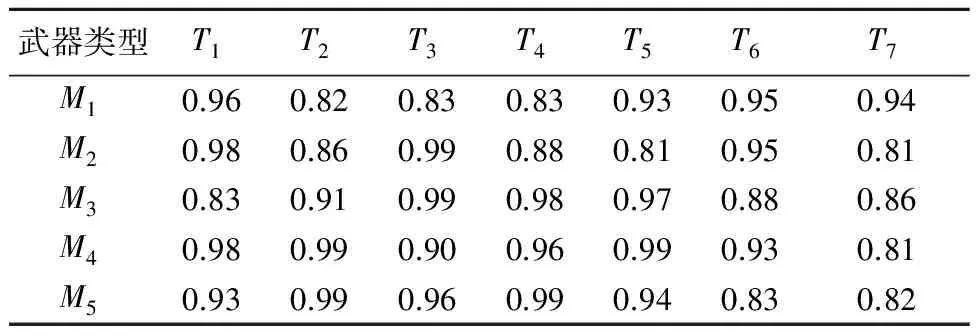
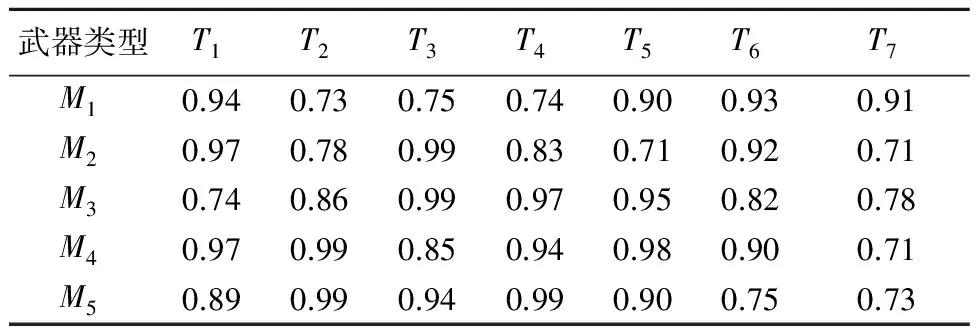
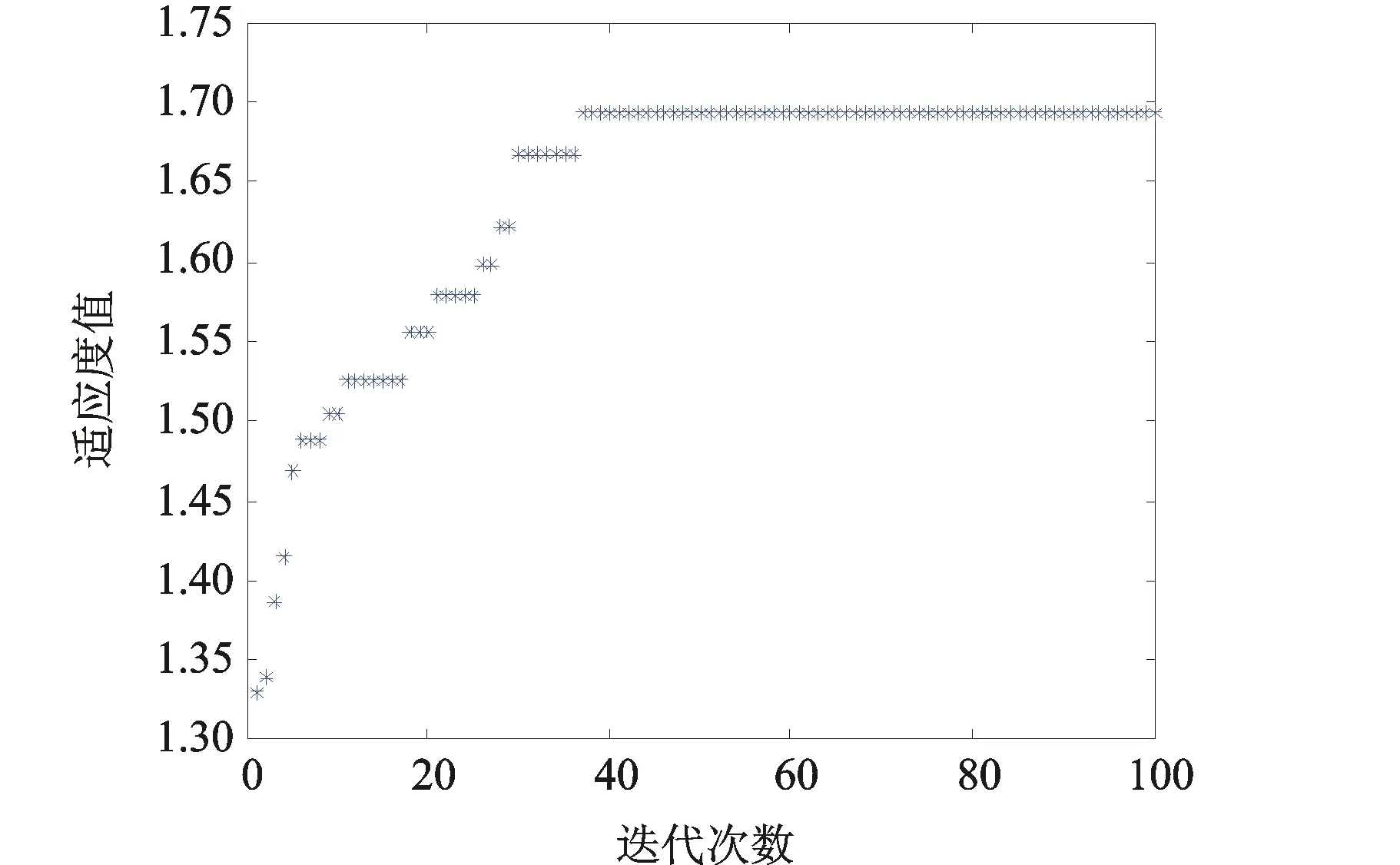
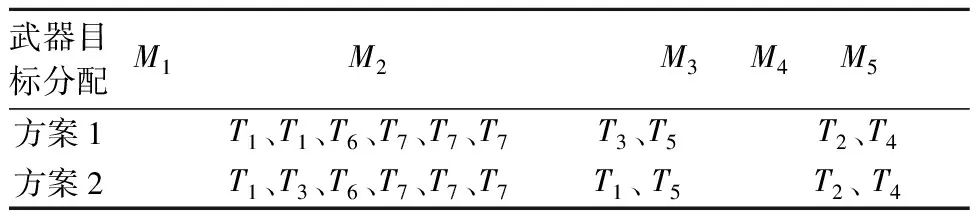
编码方式直接影响算法的搜索效率。武器的类型、数目以及目标数均为整数,本文选用整数编码表示武器与目标的对应关系。整数编码方式,能够描述武器总数m与打击目标总数n的不同情况(m>n,m 编码可以表示为x=[y1,y2,…,yh,…,ym],式中,yh为0~n之间的整数,称为元素。yh=j表示分配第h件武器单元打击第j个目标;yh=0表示第h件武器单元没有参加联合远程打击作战任务。这样就可以将武器目标分配表示为一个整数编码的解向量,也就是蝙蝠算法中蝙蝠个体的位置向量,并且这种对应关系是唯一的。 2.3.2 构造适应度函数 适应度函数,是度量个体适应度的函数,个体适应度表示种群中个体在优化计算中有可能达到或接近最优解的优良程度。 1) 目标函数。公式(3)和公式(6)作为武器目标分配问题优化的2个目标函数,属于多目标优化问题。在实际求解过程中,对附带损伤最小原则进行处理,将问题简化为单目标求解问题。实际上,若目标附带损伤程度越小,则需要消耗的武器资源就越少,相应地也能够提高作战行动的效费比。因此,可以通过限制附带损伤,将附带损伤目标函数转化为求解效费比函数的约束条件,即令 (13) 式中,ω为打击所有目标带来的附带损伤之和,求解过程中设置成常数,以控制附带损伤在可以接受的范围内。 (14) 2) 惩罚函数。根据以上分析,公式(2)和公式(13)作为优化求解的约束条件,计算蝙蝠个体适应度值时,可以通过构造惩罚函数来实现。公式(15)就是对不满足约束条件的解进行惩罚,使其对应的适应度值为负。 (15) (15) 2.3.3 小生境蝙蝠算法流程 设计小生境蝙蝠算法(NicheBatAlgorithm,NBA)的实现流程: 1) 初始化t时刻蝙蝠群的位置(也就是问题的解向量xl(i=1,2,…,n))和速度vl;初始化频率fl、脉冲频率rl和响度Al; 2) 计算种群中所有个体的适应度值,并按照适应度值从大到小对个体排序,记录前N个蝙蝠个体; 3) 根据公式(7)~(9),更新t+1时刻蝙蝠的速度和位置; 4) 产生随机变量rand1,若rand1大于rl,选择最佳位置并在该位置附近随机产生一个位置; 5) 通过随机飞行产生一个新的位置; 6) 产生随机变量rand2,若rand2 7) 小生境淘汰操作,计算每2个蝙蝠之间的欧氏距离,当距离小于预设值时,对其中适应度较小的个体予以惩罚[19]。对popsize+N个蝙蝠按适应度值进行降序排列,保留前popsize个蝙蝠作为下次迭代的初始群; 8)判断是否达到设置的迭代次数,“是”则结束计算,“否”则返回2)。 具体算法操作流程如图2所示。 图2 小生境蝙蝠算法流程 3.1 实验案例 为验证小生境蝙蝠算法求解武器目标分配问题的有效性,设计了一个联合远程打击案例。此案中,使用5种类型的武器打击7个独立目标,武器和目标的相关参数如表1和表2所示。每种类型的武器对目标的毁伤概率和突防概率数据如表3和表4所示。 表1 目标参数 表2 武器参数 表3 武器—目标毁伤概率 表4 武器—目标突防概率 3.2 仿真分析 3.2.1 参数设置 种群popsize=50,保留优秀个体数N=3,迭代次数N_iter=100,初始速度、频率用rand()函数随机产生,响度衰减系数α=0.9,脉冲频率增加系数γ=0.05,频率下限fmin=0,频率上限fmax=2,附带损伤控制量ω=1,作战效能函数的底数a=10。 3.2.2 仿真实验 使用Matlab软件对以上案例进行仿真分析,得出适应度值演化过程如图3所示,在第37次迭代过程搜索出最优解,最大效费比为1.694。 图3 小生境蝙蝠算法迭代100次适应度值演化情况 进行多次独立重复实验,求解的最大适应度值稳定在1.694,认为该适应度值为近似最优解。实验中获得2组满足近似最优解的可行分配方案,其武器目标对应关系如表5所示。 表5 分配方案 为验证本文改进算法的性能,使用传统蝙蝠算法和本文算法分别对上述案例进行100次求解实验,得到近似最优解的次数分别是21次和86次。这表明引入小生境思想的蝙蝠算法,通过控制蝙蝠个体的分布距离,有效改善了算法的全局搜索能力。 针对联合远程打击作战筹划中武器目标分配问题,提出了武器分配的基本原则并构建了数学模型,在模型求解中提出了一种改进蝙蝠算法,通过实例验证得到以下结论: 1) 本文构建的联合远程打击WTA数学模型,更好地反映了现代战争的制胜机理。 2) 引入小生境淘汰思想的改进蝙蝠算法,通过控制蝙蝠个体的分布距离,有效改善了蝙蝠算法的全局搜索能力。 References) [1]LLOYD S P,WITSENHAUSEN H S.Weapon allocation is NP-complete [C]//Proc.1986 Summer Compute Simulation Conference.Reno:[s.n.],1986:1054-1058. [2] 阮晏智,李庆民,刘天华.编队防空火力分配建模及其优化方法研究[J].兵工学报,2010,31(11):1525-1529. [3] 刘晓,刘忠,侯文姝,等.火力分配多目标规划模型的改进MOPSO算法[J].系统工程与电子技术,2013,35(2):326-331. [4] 董朝阳,路遥,王青.改进的遗传算法求解火力分配优化问题[J].兵工学报,2016,37(1):97-102. [5] 崔莉莉.基于蚁群算法的武器—目标分配问题研究[D].上海交通大学,2011:56-59. [6] 吴平,梁青.武器—目标分配问题的模拟退火算法[J].计算机工程与应用,2006(4):87-90. [7] 徐加强,毕义明,汪民乐,等.基于时空约束的常规导弹火力分配建模与实现[J].系统工程与电子技术,2011,33(9):2025-2029. [8] 吴家明,乔氏东,黄金才.基于NSGA-II的防空部署优化方法[J].火力与指挥控制,2011,36(3):57-61. [9] YANG X S.A new metaheuristic bat-inspired a1gorithm[M]//Nature inspired cooperative strategies for optimization (NICSO 2010).Ber1in Heidelberg:Springer,2010:65-74. [10] YANG X S,GANDOMI A H.Bat algorithm: a novel approach for global engineering optimization[J].Engineering Computations,2012,29(5):464-483. [11] 张最良,李长生,赵文志,等.军事运筹学[M].北京:军事科学出版社,1993:408-410. [12] 刘振林,唐苏妍,葛伟.创造性思维粒子群优化的武器目标分配[J].火力与指挥控制,2012,37(3):4-9. [13] 毛艺帆,张多林.改进的人工蜂群算法求解武器目标分配问题[J].军事运筹与系统工程,2015,29(1):30-34. [14] 李平,李长文.武器目标协同火力分配建模及算法[J].指挥控制与仿真,2015,37(2):36-40. [15] YANG X S.Nature-inspired metaheuristic algorithms[M].United Kingdom:Luniver Press,2010:97-104. [16] 郭业才,吴华鹏,王惠.基于DNA遗传蝙蝠算法的分数间隔多模盲均衡算法[J].兵工学报,2015,36(8):1052-1057. [17] 韩维,史玮韦,司维超.多交叉混沌选择反向小生境遗传算法[J].计算机工程,2014,40(6):154-156. [18] 汪民乐.遗传算法的收敛性研究[J].计算技术与自动化,2015,34(1):58-62. [19] 陆文博,刘春生,周青松,等.基于小生境遗传算法的干扰资源优化分配技术[J].电子信息对抗技术,2014,29(3):33-37. (编辑:李江涛) Research on the Modeling and Solving of the Joint Long-range Strike Weapon Target Assignment Problem Based on the Niche Bat Algorithm LIU Shuangshuang1,2, XU Ruiming1, PAN Junjie1 (1. Institute of Military Operational Research and Analysis, Academy of the Military Science, Beijing 100091, China; 2. 61569 Troops, China) Based on the combination of mathematical modeling and simulation analysis, this paper studies the basic principle of weapon target assignment of joint long-range precision strike weapon target assignment and constructs a multi-objective optimization mathematical model to solve the weapon target assignment problem in the operational planning of joint long-range precision strike. This paper processes the objective functions and constraint conditions and transforms the model into a single objective optimization problem. An improved bat algorithm is proposed to solve the approximate optimal solution of weapon target assignment. The experimental results show that the proposed algorithm can effectively improve the convergence characteristics of the bat algorithm and is suitable for solving the problem concerning weapon target assignment of joint long-range strike. weapon target assignment; joint long-range strike; bat algorithm; niche 2016-10-24 部委级资助课题(2015JY546) 刘双双(1985—),男,工程师,博士研究生,主要研究方向为联合作战方案生成与评估。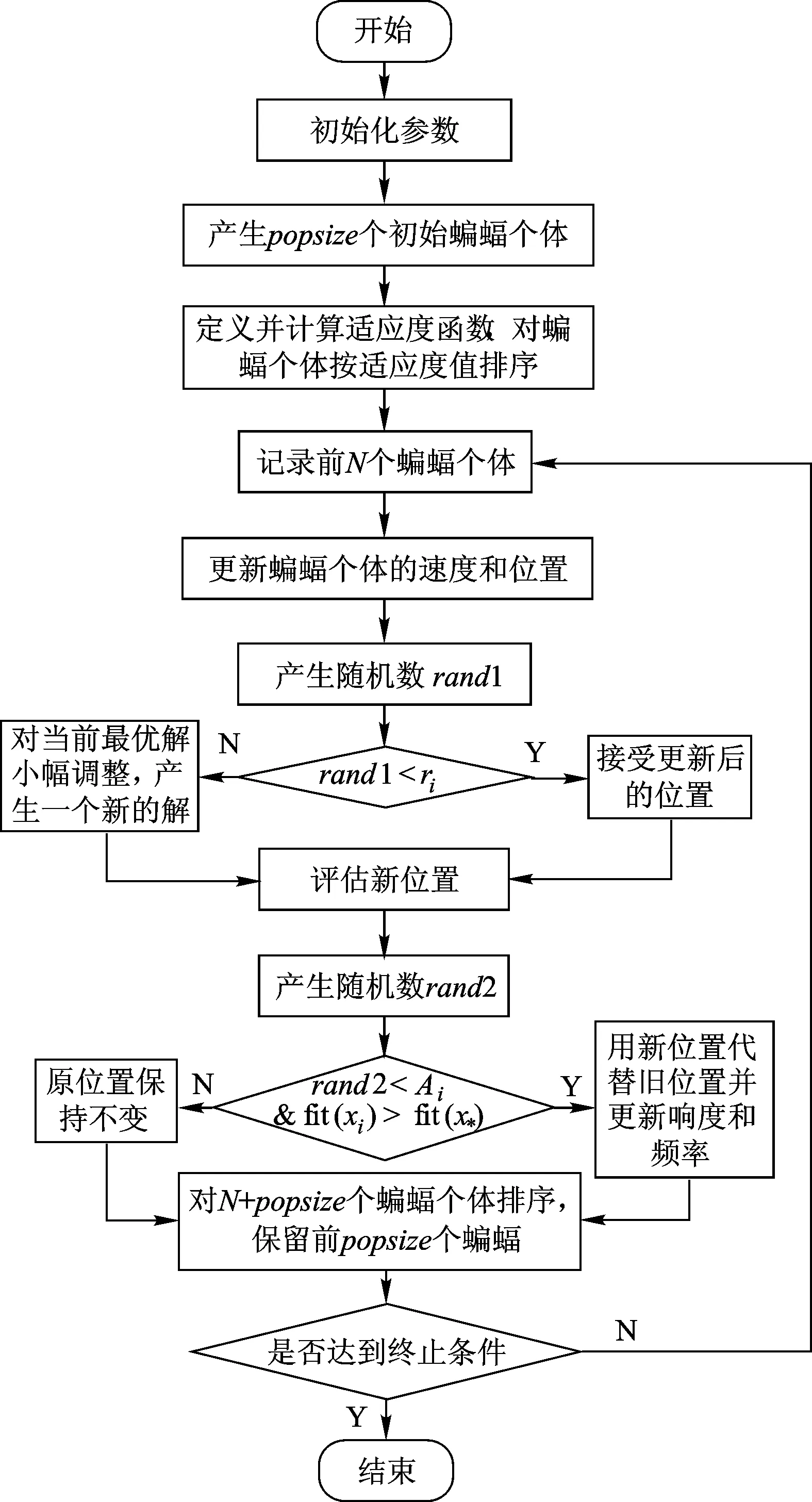
3 实例分析
4 结 论
