复杂电磁环境下北斗干扰源的协同定位技术∗

复杂电磁环境下北斗干扰源的协同定位技术∗

康荣雷

（中国西南电子技术研究所成都610036）

针对于复杂电磁环境下对北斗干扰源的定位需求，提出利用到达时间差TDOA和到达频率差FDOA的协同定位方法，建立干扰源协同定位算法的数学模型，进行迭代求解和结果评估，分析定位算法的克拉美劳下界。仿真结果表明，该方法具有较好的定位精度和算法性能。

协同定位；克拉美劳下界；到达时间差TDOA；到达频率差FDOA

Class NumberTP391

1 引言

自“导航战”概念提出至“反介入/区域拒止”能力在战场对无线电导航信号的限制，卫星导航在战场区域的可用性一直存在疑问，导航对抗也成为近年来科学研究的重点方向。其中，干扰源定位技术是导航对抗中的重要部分，识别和定位干扰源对于提升北斗在战区的使用能力具有重要意义［1～2］。

干扰源定位通常采用无源定位的方式进行，很早的时候对基于到达时间差（TDOA）、到达频率差（FDOA）等的无源定位就开展了大量的研究［3～5］。最近的研究中，将传统声学中定位信号为平稳随机信号的模型拓展到了电子系统中确定性的信号［6］，以及考虑不同协作者之间未知通道增益的场景［7］。另外一方面，考察了实际应用中非理想因素带来的影响，比如协作者位置误差［8～9］，以及存在实际应用场景中的运动干扰源位置的跟踪等［10～11］。

本文研究在复杂电磁环境下，协同平台之间利用数据链与惯导的相对导航，实现精确相对定位和时间同步能力，利用无源定位技术中到达时间差（Time Difference of Arrival，TDOA）和到达频率差（Frequency Difference of Arrival，FDOA）算法建立对北斗干扰源的定位测量模型，给出协同定位对干扰源定位的克拉美劳下界的表达式，分析多机协同的探测范围和定位精度。

2 北斗干扰源定位模型

2.1定位模型

假设在M个测站（协作者）对N个卫导干扰信号进

行侦收，图1是三个站点协同对一个干扰源定位的示意图。

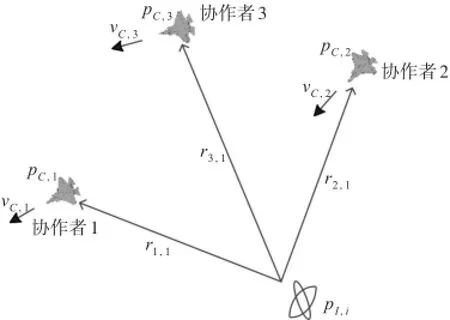
图1 多站协同高精度无源定位示意图

其中：pC,i(t),i=1,…,N表示t时刻第i个测站的位置矢量；pI,i(t),i=1,…,M表示t时刻第i个干扰源的位置矢量；vC,i(t),i=1,…,N表示t时刻第i个测站的速度，vI,i(t),i=1,…,N表示t时刻第i个干扰源的速度。

2.2观测量

在t时刻，第m个协作者与第n干扰源之间的距离rm,n(t)为

干扰信号到达各个测站的时间为距离除以光速：在第m个协作者处观测到第n个干扰源的多普勒频率为

其中fR,mn表示m站收到干扰源n的接收频率，而fT,mn表示干扰源n发出的干扰信号频率。

一般而言，干扰源为非合作目标，干扰信号的传输时间也未知，但可以通过在单个站点的频带内，对干扰信息进行采样，再通过数据链进行数据交换，从而测量到FDOA和TDOA。因此，我们做出如下假设：

假设1：各协作者之间时间同步，可以获知自己在t时刻的位置、速度。

假设2：各协作者对干扰信号进行采样，通过数据链进行数据交换，可以（通过相关、模糊函数、最大似然等方法）测量任意两个协作者在t时刻观察到干扰信号的FDOA和TDOA。

将式（1）代入式（3）可以得到由干扰源位置和速度决定的多普勒频率：

对于第p个协作者和第q个协作者观测到第n个干扰源的到达频率差为

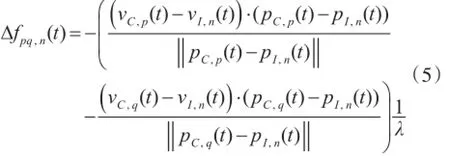
其中1 λ为窄带信号中心频率。对于第p个协作者和第q个协作者观测到第n个干扰源的到达时间差为

在实际中，并不能对FDOA和TDOA进行精确的测量，为了建模测量过程中的噪声，进一步假设：

假设3：到达频率差FDOA的测量式（5）存在噪声nΔf,pqn～N(0,σ2Δf,pqn)，TDOA的测量式（6）存在噪声nτ,pqn～N(0,σ2τ,pqn)。

假设4：FDOA测量噪声和TDOA测量噪声相关，即：

E(nΔf,ijnnτ,pqn)=cnδi,pδj,q,∀i,j,p,q∈{1,…,M},∀n∈{1,…N}。

2.3定位算法

根据上一章节中对TDOA与FDOA的测量描述，设计多站协同对干扰源定位的数学模型分别为

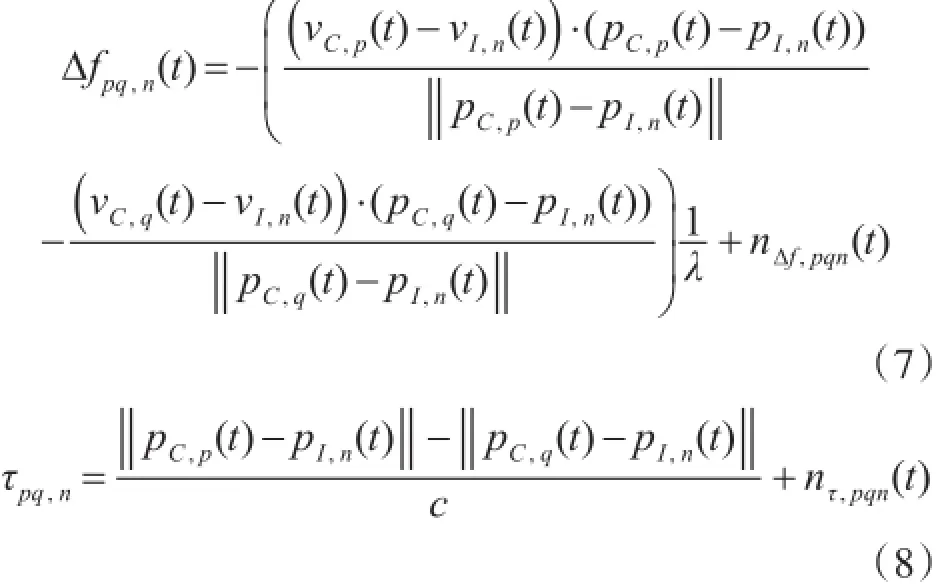
根据式（7）与式（8）求解干扰源的位置和速度，即pI,n(t)和vI,n(t)。

其中，TDOA只与目标位置相关，而FDOA与目标位置和目标速度均相关。当结合TDOA与FDOA对目标进行定位定速的时候，可以先利用TDOA确定目标的位置，然后联合FDOA和TDOA测量，同时计算目标的位置和速度。

2.3.1 定位方程

以4个协作者为例，需要求解如下方程组以获得目标位置：

从几何上看，TDOA约束式（9）：定义了一组双曲面，而干扰源位置位于多组测量定义的多组双曲面的交点；FDOA约束式（10）：定义了一组等频面，而干扰源位置位于多组测量定义的多组等频面的交点。

2.3.2 方程变换

假设M个协作者分别位于pC,i,i=1,…,M，干扰源位置矢量pI，那么根据光速可以表示由TDOA和FDOA导致的距离差与协作者和干扰源之间位置的关系，di和d1i分别表示TDOA和FDOA径向速度差：

以第一个协作者的位置作为坐标原点，建立了一个新的直角坐标参考系，此时第i个协作者的坐标为p′

C,i=pC,i-pC,1，可得：

其中x=pC,1-pI。对上式进行化简，写成关于x的方程，有：

2.3.3 方程解算

将TDOA相关方程（15）写成矩阵的形式：

根据式（17）可以写出该最小二乘估计问题如下：

其中

需要注意的是，这里有N组TDOA测量，可以是来自N个协作者在某一个时刻的测量，也可以少于N个协作者，在多个时刻不同位置处的测量的组合。

基于上述问题描述的估计算法可以分为三类：无约束最小二乘、带约束最小二乘、近似最小二乘。

类似TDOA方程求解过程，构造由式（16）方程残差组成的非线性最小二乘问题：

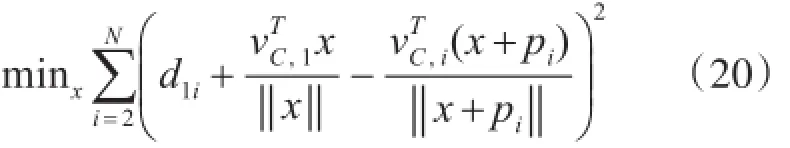
采用高斯牛顿迭代，从一个给定的初始值开始迭代，直至收敛。其中初始值，可以利用辨识性分析中得到的唯一解。

算法流程总结如下：

1）确定一个迭代初值；

2）采用高斯牛顿迭代，计算迭代后的位置值；

3）判断是否收敛，如果不收敛这进入2）；

4）解算结束，输出定位结果。

2.3.4结果评估

假设选择p=1为参考，q=2,…,N共计N-1组独立观测量为

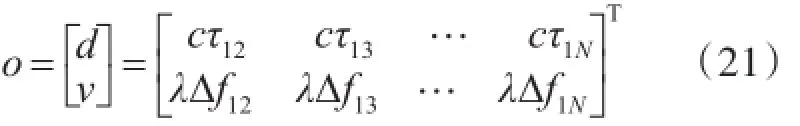
假设观测量o的噪声服从零均值高斯分布，且协方差矩阵记为Q，那么此时观测量的概率分布为：

其中：

3 仿真验证

假设五个协作者的轨迹矩阵如下：

其中第一行表示时间，第二至第四行表示坐标。采样时刻均为0s。单个目标的轨迹矩阵如下：

目标发射信号频率为1575.42MHz。仿真场景如图2所示，其中圆圈位于原点处，代表干扰源目标，黑色轨迹为协作者运行轨迹。

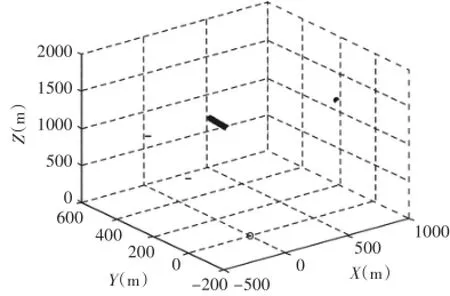
图2 5个协作者TDOA定位仿真场景

3.1干扰源定位

3.1.1 基于TDOA的定位仿真

图3给出TDOA定位算法非迭代的闭合形式的解和带约束的迭代解，从图中可以看出，闭合形式直接求解的精度与带约束直接求解的精度稍差，但差异不大，且随着噪声的加大而逐渐加大。

图3 非迭代算法与带约束迭代算法定位精度随噪声的变化

3.1.2 基于FDOA的定位仿真

图4给出协作者之间利用测量得到的接收频率差进行联合定位的结果精度随噪声的变化情况，从图中可以看出，当噪声标准差为1m的情况下，对目标的定位精度约60m；随着噪声标准差的增大，基于FDOA的定位精度也迅速增大。

图4 无约束优化FDOA定位精度随噪声的变化

其中第一个协作者与其它各个协作者之间的到达频率差分别为-30.6305Hz，-208.9279Hz，-45.7240Hz，-36.0704Hz。从结果中可以看出，如果单独使用FDOA进行定位，在只有5个协作的情况下，对测量精度的要求非常高。

当协作者的速度保持不变，但协作者距离干扰源目标的位置远离10倍的情况下，基于FDOA的定位精度变化如图5所示。从结果可以看出，定位精度也随之降低10倍。

图5 协作者距离干扰源目标距离扩大10倍后的定位精度随噪声变化

3.1.3 基于TDOA和FDOA的定位仿真

对TDOA和FDOA添加比例相等的噪声，即与TDOA测量和FDOA测量值的幅度相当的噪声，基于TDOA、FDOA或者基于TDOA联合FDOA的测量值的干扰源目标定位结果如图6所示。从图中可以看出，基于FDOA的定位结果要差于基于TDOA定位的结果，但是当联合两者进行定位时，可以取得更佳的定位效果。

图6 基于TDOA、FDOA或者联合TDOA和FDOA定位精度随噪声的变化

3.2性能分析

3.2.1 基于TDOA的克拉美劳下界

在TDOA噪声标准差为1m的时候，假设干扰源目标位置在水平面上变化时，采用单站多普勒定位的定位精度的下界如图7所示。其中5个矩形框表示5个协作者在水平面的投影，等高线所示为干扰源目标三个坐标方差之和的对数值。从图中可以看出，存在在该种协作者的状态下无法进行估计的两个点，而在其它位置，对干扰源目标的估计的GDOP值相对较低。

根据CRB工具，可以对目标位置的最优定位精度进行刻画，据此可以用于对协作者的轨迹和速度设计等。

图7 多站TDOA定位CRB

3.2.2 基于FDOA的克拉美劳下界

在FDOA噪声标准差为1Hz的时候，假设干扰源目标位置在水平面上变化时，采用单站多普勒定位的定位精度的下界如图8所示。其中5个矩形框表示5个协作者在水平面的投影，等高线所示为干扰源目标三个坐标方差之和的对数值。从图中可以看出，与TDOA定位相比，FDOA定位相对偏大，同时FDOA与TDOA的定位精度随干扰源位置变化的分布情况具有互补的趋势，根据CRB工具，可以在联合TDOA与FDOA定位时给出具有指导意义的加权组合系数。

图8 多站FDOA定位CRB

4 结语

本文研究在复杂电磁环境下，利用无源定位技术中到达时间差（TDOA）和到达频率差（FDOA）建立对北斗干扰源的定位测量模型，并对该模型的定位精度和算法性能进行仿真验证。

算法的仿真表明，在多站TDOA定位场景下，非迭代的闭合形式解与带约束的迭代算法所得到的定位结果精度相差不大，但是前者具有非常小的计算量，适合实时运算；在多站FDOA定位场景下，协作者数目越多定位精度越高，相同的多普勒测量情况下，协作者与目标之间的距离越大，定位精度越差。实际上TDOA与FDOA测量也存在“此消彼长”的关系，即对TDOA的测量准确的情况下，FDOA的测量精度往往差些，所以最好策略是联合TDOA和FDOA进行定位，仿真表明，联合求解能得到比单独求解更高的定位精度。CRB仿真分析，给出了干扰源位置在水平面变化时，根据已知固定的协作者配置关系，得到的干扰源定位精度的分布情况，与前面的仿真结果相印证，同时CRB分析还可以作为联合TDOA与FDOA定位的最优加权系数的确定。

［1］邢美丽，肖军鹏.复杂电磁环境下协同干扰技术研究［J］.遥测遥控，2010，31（4）：30-35.

XING Meili，XIAO Junpeng.Research on Cooperative Jamming in Complex Electromagnetic Environment.Jour⁃nal of Telemetry［J］.Tracking and Command，2010，31（4）：30-35.

［2］陈霄，徐慨，董蛟，等.卫星干扰源定位系统的研究［J］.信息通信，2015，8：34-36.

CHEN Xiao，XU Kai，DONG Jiao，et al.Research of the Satellite Interference Location System［J］.Information& Communications，2015，8：34-36.

［3］Smith J，J.Abel.The Spherical Interpolation Method of Source Localization［J］.IEEE J.Oceanic Eng，2003，12（1）：246-252.

［4］Chan Y T，K.C.Ho.A Simple and Efficient Estimator for Hyperbolic Location［J］.IEEE Transactions on Signal Pro⁃cessing，1994，42（8）：1905-1915.

［5］Ho K C，Y.T.Chan.Geolocation of a Known Altitude Ob⁃ject From TDOA and FDOA Measurements［J］.IEEE TRansactions on Aerospace and Electronic Systems，1997，33（3）：770-783.

［6］Fowler M L，X.Hu.Signal Models for TDOA/FDOA Esti⁃mation［J］.IEEE TRansactions on Aerospace and Elec⁃tronic Systems，2008，44（4）：1543-1550.

［7］Yeredor A，E.Angel.Joint TDOA and FDOA Estimation：A Conditional Bound and Its Use for Optimally Weighted Localization［J］.IEEE Transactions on Signal Processing，2011，59（4）：1612-1623.

［8］Kovavisaruch L，K.C.Ho.Alternate Source and Receiver Location Estimation Using TDOA with Receiver Position Uncertainties［J］.IEEE Infernation conference on acous⁃tics speech and signal processing，2005，4：1065-1068.

［9］Ho K C，et al.Source Localization Using TDOA and FDOA Measurements in the Presence of Receiver Location Errors：Analysis and Solution［J］.IEEE Transactions on Signal Processing，2007，55（2）：684-696.

［10］Ho K C，W.Xu.An Accurate Algebraic Solution for Mov⁃ing Source Location Using TDOA and FDOA Measure⁃ments［J］.IEEE Transactions on Signal Processing，2004，52（9）：2453-2463.

［11］Sun M，K.C.Ho.An Asymptotically Efficient Estimator for TDOA and FDOA Positioning of Multiple Disjoint Sources in the Presence of Sensor Location Uncertainties［J］.IEEE Transactions on Signal Processing，2011，59（7）：3434-3440.

Cooperative Location Method of Beidou Interference Sources under Complicated Electromagnetic Environment

KANG Ronglei
（Southwest China Institute of Electronic Technology，Chengdu610036）

Under the complicated electromagnetic environment for positioning requirement of beidou interference sources，a co-location method is proposed based on Time Difference Of Arrival（TDOA）and Frequency Difference Of Arrival（FDOA），and the interference sources of collaborative localization algorithm is modeled mathematically，which is solved iteratively.An assess⁃ment on the results is made and Cramer Rao lower bound of the localization algorithm is analyzed.The simulation results demon⁃strate that the method has better precision and algorithm performance.

co-location，Cramer Rao lower bounds，time difference of arrival，frequency difference of arrival

TP391

10.3969/j.issn.1672-9722.2017.05.014

2016年11月12日，

2016年12月13日

康荣雷，男，工程师，研究方向：卫星导航定位。