思考——学习数学的有效途径

◎黄建东

(无锡市八士中学，江苏 无锡 214192)

思考
——学习数学的有效途径

◎黄建东

(无锡市八士中学，江苏 无锡 214192)

数学千变万化，但是基本知识点不变，如何使学生在知识迁移和知识应用上得到发展，离不开教师平时的教学思考，培养学生学习数学的思考.在平时的教学中要培养学生的数学思考、数学分析能力、题目知识点的分解能力，通过教师的引导、示范，让学生参与数学课堂的思考，从而培养学生的思考能力，让学生真正掌握学习数学的有效途径——思考.

数学；思考

数学是一门应用型学科，对于中学数学而言，应用主要体现在知识的迁移和知识的应用上，特别是2016年1月八年级数学学业水平测试，最能体现数学知识的迁移和应用.总分120分的数学试卷，共有26题，10个选择题，8个填空题，8个解答题，整张试卷的编排基本上采用中考模式，难度在0.7左右.其中填空、选择最后一题较难，22、23、24大题需要分类讨论，才能完整解答.25题第二问需要学生转化题目条件，利用已有知识构建桥梁，完成解答，得分率极低.26题需要学生通过数形结合，完成应用问题的函数题，得分率较低，仅为32%左右.分析学生解答试卷情况，主要是学生不会利用知识，对知识的迁移能力不够，缺乏必要的分析和思考，本次考试对今后的数学教学有一定的指导意义.

数学千变万化，但是基本知识点不变，对学生答题情况分析后可以发现，我校学生试卷答题情况呈现的主要是缺少对题目必要的数学思考，数学分析能力、分解能力的不足，对相关知识链接、整合能力不足，导致解题的不完整和错误.

所以，我们数学教师要有敏锐的眼光并积极地思考，平时在教学中要注重分析和启发，引导学生思考，发现有价值的问题，点燃学生思考的火炬，课堂引领学生思考数学，学习数学，领悟数学.

一、理解数学思考的特点

数学思考也就是数学思维的训练，它和学生已有知识、能力以及分析问题的能力有着密不可分的关系.思考是一种个体行为，具有鲜明的个性特征，主要表现为猜想、联想、质疑、反思和推理等.

猜想，是大脑对已有的零散的表象进行合乎逻辑的加工而形成新的思维的过程，特别适合先猜想后证明的数学问题，有助于启迪学生的数学思维，是逻辑推理必要的补充.

联想，是大脑对某些信息进行加工，提取类似或相通问题的一种思维过程，它是数学思考的重要组成部分，也就是我们常说的举一反三或触类旁通.联想有助于信息的对比或借用，能更深入地思考问题的本质，让数学思考具有更大的深度和广度.

质疑，就是提出问题，有人说提出问题比回答问题更重要.数学考试题难，主要就是难在对题目的分析、梳理和整合上，而质疑恰好就是分析为什么的起点，也是数学思考最本质的表象，教师要重视质疑，也要鼓励学生质疑，因为这是思考的起点.

反思，学而不思则罔，现有质疑而后就要努力反思，从表象入手，寻找问题的症结所在，从而完成数学思考，反思有助于更深入地理解问题的本质，加深思考的深度.

推理，是以上思考呈现结果，体现了思考的延展性和逻辑性，能更好地服务于思考.

数学教学中的思考，要充分体现学生的真思考和真实践，教师不能越足更不能矫情地假思考，否则只会是填鸭式的灌输，不利于学生思考的发展和提升.

思考不仅仅属于每一名学生，也应该属于每一位教师，只有师生共同参与的真思考，才能最有效地促进学生的数学思考.

二、营造数学思考的氛围

教师要培养学生的思考能力，首先，要营造思考的氛围，使教师成为思考的促进者、鼓励者和帮助者，以灵活的教学方式来展开对话，引导学生思考，从而培养思考能力.

(一)认识学生的潜能

课堂是学生最重要的创造之地，思考是创造的必由之路，教师要充分认识学生的思考能力是师生共同思考碰撞智慧的前提.学生思考能力是巨大的，教师要相信学生，张扬自己的个性，激发学生思考的强烈欲望，让课堂中充满思考的芬芳.

(二)点燃思考的火炬

每一名学生大脑中都有期待被点燃的火炬，教师要做的就是以自己对教学内容的感悟和见解，寻找教学的切入点，创造时机，撞出思考的火花，点燃学生思考的火炬.

让学生进行思考，要有针对性，对于初一学生而言，应注重感悟和猜想；对于初二学生而言，要注重积累和拓展；对于初三学生而言，要突出理性思维.教师要努力在不同年级逐层、深入地培养独立思考、猜想、联想、质疑、反思、推理的能力，只有这样的思考，才能使学生想得深、悟得透，真正走进数学思考的大门.

(三)升华师生的情感

教与学是一个双向运动的过程，学生潜在能力的激发，必须要有教师的激发，才能达到双向师生情感的升华.以七年级数学上中的“垂直”一课为例，课堂上为了引入垂直的概念，我选取了生活中的人们过人行横道的例子，让学生体会“垂直”的感觉，学生争先恐后地回答自己的思考结果.然后我又通过学生自己动手旋转圆规的两边，使圆规的两边处于“垂直”的状态，让学生体会“实践”的感觉，思考垂直的条件.再通过观看跳水运动员入水姿势判断水花大小的视频，反思如何才算两条直线垂直？通过以上3个片段的师生互动和对话，让学生在交流中加深理解垂直的概念.整个引入过程自然，师生相互感染，课堂氛围活跃，加深了师生的情感.

三、创建数学思考的平台

数学的本质是数学学习的思考源，教师要善于挖掘题目的信息，带领学生进入思考的胜境，品味思考的来源、过程、和感悟.

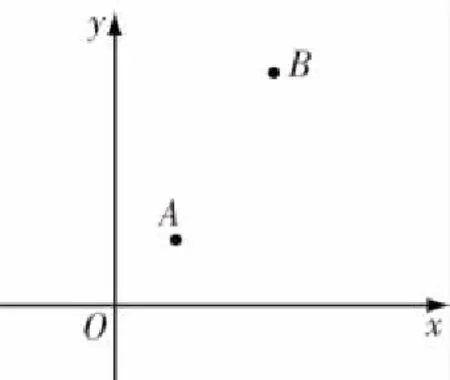
(2016年1月八年级试卷第10题)在平面直角坐标系中，已知A(1，1)，B(3，5)，要在坐标轴上找一点P，使得△PAB的周长最小，则点P的坐标为( ).

A.(0，1) B.(0，2)

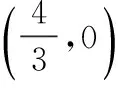
平时对于此类题目的思考就是：首先，要利用对称在x轴，y轴上找到得到点P的方法，然后，需要用待定系数法求出AB直线的解析式，得出点P的坐标，学生大多选择了D，两种解答.忽略了最后还要比较两种方法中的点P哪一种使得△PAB的周长最小，最小中找到最小的答案，得出正确答案.

(2016年1月八年级试卷第26题)如图1，某物流公司恰好位于连接A、B两地的一条公路旁的C处.某一天，该公司同时派出甲、乙两辆货车以各自的速度匀速行驶.其中，甲车从公司出发直达B地；乙车从公司出发开往A地，并在A地用1h配货，然后，掉头按原速度开往B地.图2是甲、乙两车之间的距离s(km)与他们出发后的时间x(h)之间函数关系的部分图像.

(1)由图像可知，甲车速度为________km/h；乙车速度为________km/h.

(2)已知最终乙车比甲车早到B地0.5h，求甲车出发1.5h后直至到达B地的过程中，s与x的函数关系式及x的取值范围，并在图2中补全函数图像.

图1

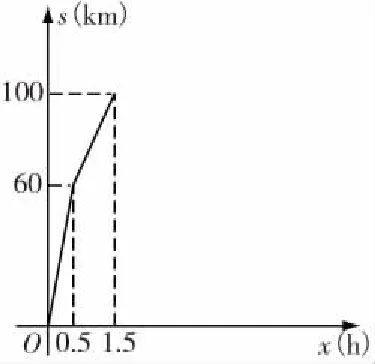
图2

首先，图像中点(0.5，60)表示两车0.5小时路程和，点(1.5，100)表示乙车0.5小时和甲车1.5小时路程和，易得甲车速度为40 km/h；乙车速度为80 km/h.

此时乙车开始追甲车，追击路程为100 km，设追击时间为x小时乙车追上甲车.80x=100+40x，解得x=2.5，乙车追上甲车的坐标为(4，0).

因为最终乙车比甲车早到B地0.5 h，说明追上后，乙车比甲车多跑了0.5×40=20 km.

设乙车追上甲车后y小时到达B地,80y=40(y+0.5)，y=0.5，乙车到达终点B的坐标是(4.5，20)，甲车到的终点坐标(5，0).

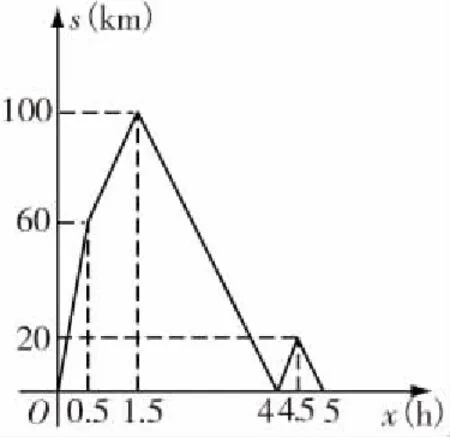
由待定系数法求得解析式，并画出图像.

(2)当1.5≤x≤4时，s=-40x+160;

当4

当4.5

其实本题主要考查的就是数形结合的思想，由已有图形得出两车的速度，利用追击问题求出时间，得出点坐标，求出解析式，画出图像.

在《数学课程标准》中，数学思考成为四维目标之一，数学思考中至关重要的部分就是思维能力，因为这是所有学生认识事物的普遍现象，但是这种能力的培养不是一蹴而就的，需要教师持之以恒的不断努力，在平时的教学中，不断尝试、不断实践.

如果把思考能力展现在数学中发生比喻为“台上三分钟”的话，那么平时的思考能力培养就是“台下十年功”.教师，只有在平时的数学教学中充分挖掘、培养学生的数学思考能力，才能更好地落实在数学课堂.教学中的数学思考，真正让学生在数学思考方面有长足的进步.