事件相互独立和互斥关系的探讨及举例
2017-06-01蔡文丽
◎蔡文丽
(中国矿业大学(北京)理学院,北京 100083)
事件相互独立和互斥关系的探讨及举例
◎蔡文丽
(中国矿业大学(北京)理学院,北京 100083)
本文全面分析两事件相互独立与两事件互斥的关系,并通过典型事例展现二者关系.研究结果对学生学习概率论课程具有重要指导作用.
独立事件;互斥事件;独立和互斥的关系
一、事件相互独立和事件互斥的定义及关系
独立和互斥是概率论中两个非常重要的概念,直观而言,学生极易将这两个概念混淆并认为独立就是互斥.然而,通过理论分析,可以详细说明两者间的关系.下面通过定义、定理、注释和举例逐步揭开两者之间的关系.
盛骤等[1]给出两事件相互独立的如下定义:
定义1 设A,B是两事件,若满足等式P(AB)=P(A)P(B),则称事件A,B相互独立,简称A,B独立.
由这个定义可以证明如下重要结论:
注释1 必然事件和不可能事件与任何事件都相互独立.
证明:设A是任意事件;S和∅分别为必然事件和不可能事件.于是,P(S)=1,P(∅)=0.因此,P(AS)=P(A)=P(A)P(S),P(A∅)=P(∅)=P(A)P(∅).
定理1[1]设A,B是两事件,且P(A)>0,则A,B相互独立⟺P(B|A)=P(B).
这个定理利用条件概率的定义和事件独立性的定义可以比较容易地证明.
注释2 这个定理表明:事件A与B呈现出某种独立性意味着事件A的发生对事件B发生的概率没有影响.
定义2[1]设A,B是两事件,若AB=∅,则称事件A,B互斥(或互不相容).
注释3 两事件互斥意味着两事件不能同时发生.
注释4 不可能事件与任何事件都互斥.
定理2 两事件独立和两事件互斥没有必然关系.
证明:这个定理可以通过一系列反例说明.
(1)不可能事件与任何事件既独立又互斥.
(2)必然事件与除不可能事件外的任何事件都独立但不互斥.一般地,若P(A)>0,P(B)>0,且事件A,B相互独立,则由事件独立的定义可知P(AB)>0,于是AB≠∅,即A,B一定不互斥.这说明事件独立不能推出事件互斥.
(3)当两事件互斥且概率都大于0时,也可由独立和互斥的定义推出这两个事件一定不独立.这说明互斥不能推出独立.
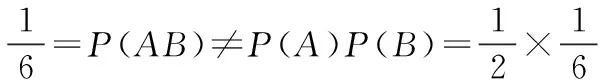
下面通过一个有趣的抽牌试验让大家体会两事件不互斥但可以独立.
二、应用举例
实例1 从一副不含大小王的扑克牌中任意抽取一张,记A={抽到8},B={抽到牌的花色为红色},考察这两个事件的互斥性与相互独立性.
显然AB≠∅,即A,B不互斥.
经计算可知
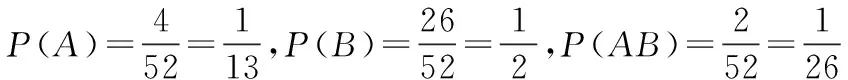
于是P(AB)=P(A)P(B),由定义可知,事件A,B相互独立.
这个简单的实例有助于读者深刻理解不互斥的两事件可以相互独立.
三、结 论
本文对高等教育出版社第四版的《概率论与数理统计》中讲授的事件独立性和互斥性内容进行了深入剖析,得出在无任何假设条件下事件独立性与互斥性没有必然联系的结论.这一结论的证明过程也蕴含着一个常用结论:对概率大于0的两事件,独立一定不互斥,互斥一定不独立,即独立和互斥不能同时成立.这一点与人们的主观认识恰好相反,值得读者注意.
[1]盛骤,谢式千,潘承毅.概率论与数理统计(第四版)[M].北京:高等教育出版社,2008.

国家自然科学基金天元专项基金资助(项目号:11626228).
