三重积分的球坐标计算方法探讨
2017-06-01河南工业职业技术学院余小飞
数学大世界 2017年12期
河南工业职业技术学院 余小飞
三重积分的球坐标计算方法探讨
河南工业职业技术学院 余小飞
在三重积分的计算过程中,有时考虑将直角坐标转化为球坐标求解,本文将研究三重积分的球坐标计算方法。
三重积分;直角坐标;球坐标
一、球坐标计算方法

在球面坐标系中,三组坐标面分别为:
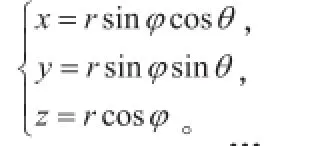
于是,三重积分可化为球坐标系下的三重积分为:


二、例题研究

解:由球坐标变换,积分区域可以表示为:
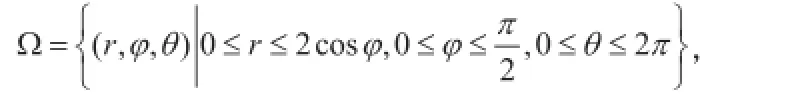


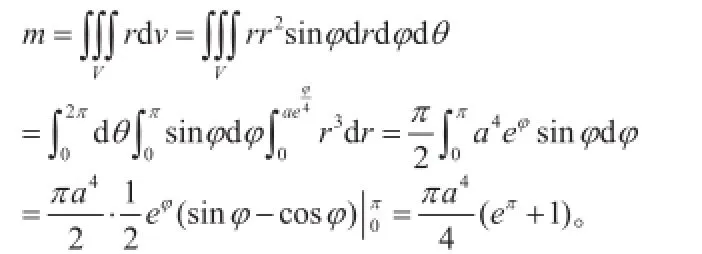
由此例可知,极坐标系下曲线绕极轴旋转一周得到的旋转面所围成的立体上的三重积分,也可以考虑在球坐标系下计算。
总之,重积分的计算,首先要画出积分域,根据积分域及被积函数选取坐标系,当积分域为球面、球面与锥面、球面与球面等围成的区域,而被积函数中含有“”时,我们考虑使用球面坐标变换求该三重积分。
[1]费定辉,周学圣.数学分析习题集题解[M].济南:山东科学技术出版社,2008:368-369.
[2]华东师范大学数学系.数学分析[M].第三版下册.北京:高等教育出版社,2006:247-251.
[3]裴礼文.数学分析中的典型问题与方法[M].北京:高等教育出版社,2004:709 -718.
余小飞,性别:男,籍贯:河南镇平,学历:大学本科,理学硕士学位,职称:讲师,研究方向:基础数学)
