对笔算除法教学难点的思考

孙滨

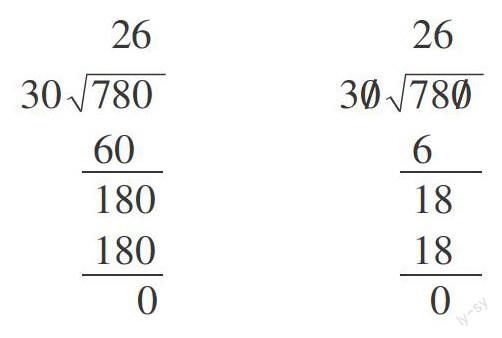
笔算除法在小学阶段是一个重要的学习板块。笔者在教学过程中发现，当过了一个学期或者一段时间后，大部分学生对笔算除法便又停留在模糊记忆的层次。这让笔者不禁产生了疑问，为什么学生这么容易忘记笔算除法？笔算除法到底难在哪里？学生的思维断点到底在哪里？

一、笔算除法难在哪里？

1.书写格式

除法竖式为什么要写成这样的分层形式？为何不写成跟加减乘一样三行的形式？事实上，除法竖式的分层书写是表示除法的过程和结果的需要，它的优势是既能表示出商与除数的积，又让余数有了位置。这两个数即是运算过程的表达，也是理解算理的过程，更是理解有余数除法的关键点。特别是运算多位数除法时，这种优势更是显而易见。

2.负迁移

除法竖式是个全新的知识，容易受加减竖式的负迁移。从学生的学习来看，学生先学表内除法竖式，容易将“商×除数”这一步虚化成抄写被除数。即使教师在教学过程中刻意强调了笔算除法的运算法则，学生依然是一头雾水，只好“照搬硬套”。有人认为，用“有余数除法”引入，可以避免这个非本质的定势和干扰。然而，笔者认为这不符合知识的内在逻辑顺序。

3.方法多变

除法竖式相对其他三种运算来说，变化多端。有时商在最高位上，有时首位不够除，要看前两位；有些“0”要移下来参加计算，有些可以省略计算；有些余数要添0，有些商要添0；试商又是除法运算特有的难点，等等。方法的多变，使学生理解、掌握也变得更难。

二、笔算除法教学策略的探讨

1.科学呈现算理与算法

观摩了俞正强老师的《笔算除法》（三年级）对我有了启发。首先，通过加法、减法、乘法竖式与除法竖式的对比，引发学生强烈的认知冲突，引导学生发现并提出问题：为什么除法竖式长得这么“怪”？从而讨论出除法竖式如果像加法、减法、乘法竖式这么写，余数便没有位置写。继续讨论，三行的竖式形式余数也可以有位置写（直接写在商的后面，中间用省略号隔开），再次引发学生的认知冲突。当学生“山穷水尽”之时，通过简单的分圆片，理解“我的15与你的15有什么不同”“哪个算式更像把45平均分成3份的意思”，使学生直观地感悟竖式代表了除法的意义和过程的记录，从而使学生理解45÷3=15的笔算过程便顺理成章了。通过孩子自己的苦苦思辨，教师的巧妙引导，此时此刻的学生一定有拨云见日、豁然开朗的感觉！

这也让笔者回忆起二年级下册开始教学《笔算除法》时，学生存在这样的疑惑，为什么除法竖式这样写，教师是否正面地回答？是否有采取通俗易懂的形式让学生感悟？俞老师便做到了正视学生学习之惑，引发学生不断地提出质疑，发现问题，寻找缘由，引导孩子回到除法的意义，感悟数学的形式意义。

那么，除法竖式的第一次亮相又该以什么形式出现？怎样教书写的顺序？这是每一位教过本节课教师的困惑。很多教师让学生探究除法竖式怎么写，学生绞尽脑汁创造出了许多写法，最终还是听教师“从头道来”。如此探究，只是课堂上多了一种形式化的探究教学而已。而除法竖式的书写形式是经过了多年的多次完善的结果，让学生去创造显然是不切实际的。所以，笔者认为用有意义的接受性学习方式是比较可取而高效的。

计算教学中算理与算法是一个不可分割的整体，算理是通过算法来表现，算法又能体现出算理，算法的掌握应该和算理的理解统一起来。当学生积累了丰富的感性知识之后，通过对算理与算法的有效联结，充分体验到算理到算法的演变过程，对算理的理解就会更深刻，对算法的掌握更扎实。教师要寻求好算理与算法的平衡点，使教学扎实又不失灵活。

2.准确把握生长点与思考点

笔算除法教学中要注意在学生的各种算法中关注新知识的生长点，在关键处及时追问，促进学生知识的迁移。如教学《除数是整十数的笔算除法》一课。

师：商为什么写在个位上？

生：3在十位上，表示30，30×30=900，已经超过92了。

师：还有谁想说？

师：这里十位上9可不可以除以30，对吗？那你们认为9除以30夠除吗？（不够）所以除数是整十数，我们先看被除数的前几位？

生：前两位。

师：这里我们除到了什么位？

生：个位。

师：那么，就要把商写在……个位的上面。

学生容易从乘法的角度分析讨论，此处教师应势利导，抓准笔算除法的关键点，追问“十位上的9可不可以除以30”，为学生的后续探究提供了思路。

从而，以此为生长点教学后面的178÷30，多把讲台交给学生，引发学生暴露试商的过程，并与30×（ ）<178联系起来，容易分析总结得出：除数是两位数的除法，要看被除数的前两位，前两位不够除，就要看被除数的前三位。不仅使全体学生学会了试商的技巧，还得出了计算法则。其次，笔者还发现部分学生对算法中“除到被除数的哪一位，就在那一位的上面写商”不理解，因此，特别是在起始课中，教师还应抓准知识的生长点多让学生说一说以巩固算法。

教师还可充分利用课堂中的方法多样化、错例等生成资源，引导学生思考探究。

出示：一个三位数除以两位数，要使商是一位数，被除数最高位可以填几？

师：你能找出所有的填法吗？

（鼓励学生思考，留给学生充分的思考时间。）

生1：被除数的最高位可以填1、2、3。

师：你是怎么想的？

生1：比如19除以40，十位上不够商1，填2、3，十位上也不够商1，所以商都是一位数。

师：只要怎么做就能保证商是一位数？

生2：只要被除数的前两位比除数小，就能保证商是一位数。

生3（迫不及待）：老师，我还有方法！

师：哦？说说看！

生3：商的位置上填9。

师（一愣，继续追问）：你是怎么算的？

生3：因为9×40=360，被除数的最高位最大是3，所以可以填1、2、3。

师：你们觉得她的方法怎么样？

生4：我觉得她的方法挺方便的。

师：是呀，多么巧妙的方法啊！而且还根据商最大能填6，算出了被除数的最高位最大只能填3。

学生通过独立思考、推理找到准确答案，不仅提炼出了三位数除以两位数商位数的数字特点，还将乘法与除法进行联系，发散了学生的思维。教师在教学中应努力创设真正适合学生思考的问题，使学生在交流中碰撞出思维的火花，引发学生创造出有价值的问题。

3.合理进行比较总结与拓展提高

针对笔算除法方法的多变，在教学时应该让学生多比较，并加强当堂练习。

（1）比较总结

每学一个新知识，就让学生对新旧知识进行比较，有什么不同点和相同点，关于这些不同点、易混淆点如何区分、理解，这样更有利于学生总结出新知识的特点和笔算方法。如教学“应用商的变化规律”使笔算简便的方法。

师：比较这两种方法有什么相同点？

生1：商都一样。

生2：都没有余数。

生3：计算的结果都是一样的。

师：有什么不同？

生1：一个不划“0”，一个划“0”。

生2：左边的中间的过程和右边的过程不同。

师：能说得更具体详细些吗？

生2：左边的是60，右边的是6，左边的是180，右边的是18。

师：为什么会出现这样的差异？

生3：因为左边的是2乘30等于60，6乘30等于180，右边的是2乘3等于6，6乘3等于18。

师：还有什么不同吗？

生4：商的位置不同。

师：为什么商的位置会不同？

生5（迫不及待）：因为左边的是先算78除以30，商2，写在8的上面；右边的是先算7除以3，商2，应写在7的上面。

师：你的意思是说除到哪一位……（商就写在哪一位的上面）

生6：我还发现了最后那个“0”的位置也不同。

师：哦？这又是怎么回事？

生6：因为左边的是180减180，“0”当然写在“0”的下面，右边的是算18减18，0自然就写在8的下面了。

师：关于这种被除数和除数末尾都有零的笔算方法，你想提醒同學们什么？

生：……

师：那么下面两种方法又有什么不同？（出示学生计算过的840÷50的两种笔算方法）

生：……

学生在比较中对算理和算法有了更全面的认识。

（2）多进行当堂练

运算能力是在不断地运用数学概念、法则、公式，经过一定数量的练习而逐步形成的。本文所阐述的“练”，不是教师出题让学生做的机械练习，而是在学生比较总结出这节课算式的特点后，让他们自己照样子创造同类型的题目，再进行练习。学生在创造中一次又一次总结这些算式的特点，这样的教学更有利于学生对算理及算法的理解和掌握。

笔算除法教学中，教师应坚持“以学定教”，一切从学生的角度看问题，充分暴露学生的原有水平，根据学情有针对性地设计教学，“从学生中来，到学生中去”，呈现给学生利于建构的学习材料，让学生感觉到其实笔算除法离自己很“近”，很“真实”，真正触动学生的内心需求、拨动学生的心弦，这样才能让笔算除法教学做得更加合理、高效。

（作者单位：浙江省乐清市丹霞路小学）