一种去冗余抽样的非平衡数据分类方法

史颖，亓慧

(1.太原师范学院 科研处,山西 晋中 030619;2.太原师范学院 计算机系,山西 晋中 030619)

一种去冗余抽样的非平衡数据分类方法

史颖1，亓慧2

(1.太原师范学院 科研处,山西 晋中 030619;2.太原师范学院 计算机系,山西 晋中 030619)

欠抽样是一类常见的解决非平衡数据分类的技术。传统抽样方法(如Kennard-Stone抽样和密度保持抽样)只考虑保持数据分布。已有欠抽样方法侧重抽取分类边界附近的样本,这样抽取的样本可能改变数据的原始分布特征,从而影响分类效果。提出数据冗余度的概念,即如果一个多数类样本处于多数类的密集区且距离分类边界或少数类样本较远,则样本冗余度较高。去冗余抽样(Redundancy-removed Sampling,RRS)采用传统抽样规则去掉多数类中冗余度相对较高的样本。这样的样本子集尽量包含对分类最有帮助的样本和保持原始数据分布,且两类样本数量相对均衡。实验结果表明,经RRS抽样的分类结果的总体精度高于其他抽样方法,尤其在分类精度较低的数据集上。同时,少数类样本的判别精度也有所提高。

非平衡数据;分类;抽样法;去冗余抽样

0 引言

在实际的模式识别问题中,有很多原始数据是非平衡的,即不同类别下的样本量差别较大,如诈骗网站远少于正常网站,癌症患者远远少于非癌症患者等。通常人们对数据中稀有类别的学习有着更为浓郁的兴趣。然而多数分类算法是针对相对平衡的类分布或相等的误分损失而设计的。当处理非平衡数据时,模型的分类效果不尽人意,尤其是类别之间的误分率通常差别较大[1]。

非平衡数据自提出以来持续受到学者的关注和研究。目前常见的非平衡数据分类方法主要有:抽样方法(Sampling Methods)、代价敏感法(Cost-Sensitive Methods)、集合划分法[2]、基于核的方法[3]以及主动学习[4-5]等。采样方法主要是通过增加少数类样本或减少多数类样本使得样本相对平衡[6-7]。代价敏感法采用不同的误分代价或损失来处理非平衡数据分类问题。本文主要研究非平衡数据的抽样学习方法。

最简单的抽样方法是随机重抽样和欠抽样,即随机复制一些少数类样本或随机删除多数类样本。然而随机复制样本并没有增加样本的信息,甚至有可能导致过拟合[8]。而随机删除样本可能删去一些比较重要的(如类别边界附近)样本。简单集成法(EasyEnsemble)[9]将多数类样本集随机划分为若干个子集,并将这些子集分别与少数类样本集建立若干分类模型,最终将其集成。文献[10]提出了3种欠抽样法,NearMiss-1, NearMiss-2和“most distant”。 NearMiss-1是抽取那些到最近的三个少数类样本距离均值较小的多数类样本;NearMiss-2是抽取那些到最远的三个少数类样本距离均值较小的多数类样本;“most distant”是抽取那些到最近的三个少数类样本距离均值较大的多数类样本。考虑到随机复制样本的不足,文献[11]提出了经典的SMOTE算法,其核心思想是将少数类样本和其近邻进行线性组合从而生成新的少数类样本。后续很多学者将其改进,形成新的方法,如Borderline-SMOTE[12]、SMOTEpTomek[13]、SMOTEBoost[14]。基于聚类的抽样算法可以根据特定的问题对多数类样本进行削减,从而处理非平衡问题。面向非平衡数据的抽样方法通过新增少数类样本或删除多数类样本使得样本趋于平衡,然而在增删的过程中免不了会改变多数类或少数类的样本分布,这样就会对分类边界产生影响,进而干扰部分数据的正确分类。一般多数类误分为少数类的代价要大于少数类误分为多数类的代价[15-16]。

除上述非平衡数据抽样方法外,还有其他常规抽样方法,如Kennard-Stone(KS)抽样、Kohonen(KH)抽样、SPXY(sample set partitioning based on joint x-y distance)和密度保持抽样(Density-preserving sampling,DPS)等[17]。文献[18]在用神经网络做分类的结果表明,采用KS抽样要优于随机抽样、系统抽样和KH抽样。文献[19]中偏最小二乘回归的研究结果表明SPXY抽样效果好于随机抽样和KS抽样。文献[20]经过DPS抽样的多个分类模型的误差估计精度与分层10折交叉验证方法相差不大,但前者稳定性更高。综合上述研究可见,KS和DPS是相对较好的抽样方法。然而这些传统抽样方法并未见用于非平衡数据的抽样及分类,因此将这两种方法引入非平衡数据的欠抽样技术[21]。

本文从欠抽样的角度解决数据非平衡问题。鉴于非平衡抽样的分布可能不稳定,常规抽样没有考虑样本对分类的重要程度,利用所定义的样本冗余度挑选多余的样本,借助常规抽样的规则确保抽样的分布稳定性。这样的去冗余抽样可以兼顾多数类样本分布和分类边界,尽量去除对分类结果影响不大的样本,从而获得满意的分类结果。

1 抽样方法

目前常采用的欠抽样方法主要有以下几种:随机欠抽样(RS)随机删除多数类样本,使得两类样本数平衡;NearMiss-1 method(NM-1)抽取那些到最近的三个少数类样本距离均值较小的多数类样本;NearMiss-2 method(NM-2)抽取那些到最远的三个少数类样本距离均值较小的多数类样本;Most distance method(MD)抽取那些到最近的三个少数类样本距离均值较大的多数类样本;Cluster-Based Sampling(CBS)采用k-means聚类,选取距离类中心最近的样本为各类的代表样本。

非平衡数据容易使得分类边界倾向于少数类,即可能将部分少数类样本错分为多数类样本。欠抽样方法可以解决数据量上的不对等,然而上述欠抽样方法抽取的样本子集可能会改变原始样本的分布特征,进而影响分类效果,图1的实验结果说明了这一问题。

Fig.1 Influence of the data distribution on classification图1 数据分布对分类面的影响

原始数据均匀分布在[0,1]*[0,1]的二维平面内,真实分类面是一个反比例函数(图1中的虚线)。图1中分别包含了146个正类样本和239个负类样本。虽然正负类样本数量相差不大,但正类样本在下方较为稀疏,这样就与原始的均匀分布有所区别。最终导致分类面向正类的稀疏部分产生偏移,即有部分正类样本会误分为负类。因此,抽样子集的分布可能干扰分类边界。在做欠抽样时需要尽量保持数据的分布不变。

为保持样本分布,简要介绍两种欠抽样算法。

KS抽样算法

用于欠抽样的KS方法是对多数类样本进行KS抽样使得两类样本数平衡。

DPS抽样算法

经过DPS抽样后原始集合被划分为两个近似同分布的集合。通过子集再次DPS抽样可以将集合再一次变小,直到达到所需规模。用于欠抽样的DPS-1是采用DPS方法将多数类样本划分为同分布的若干个子集,将与原多数类数据集相似度最大的子集作为新的多数类样本集。用于欠抽样的DPS-2与DPS-1的区别在于它选择与原多数类数据集相似度最小的子集作为新的多数类样本集。

2 去冗余抽样

如果两个多数类样本距离较近且距离少数类样本较远,则认为这两个样本是冗余的,有一个多数类样本可去除。这样的去冗余处理一方面尽量保持了多数类样本的分布,同时将距离边界或少数类样本较远的多数类冗余样本做了缩减,这样就兼顾多数类样本的同分布性质和样本的重要度。

RRS算法

虽然两个距离少数类样本较远且彼此较近的多数类样本是冗余的,但如果将两个样本都去除,则数据的分布很容易产生变化,本文提出的RRS算法是将一个去除,另一个保留,这样就兼顾了样本的冗余程度和数据的整体分布。

3 实验结果及分析

(1)实验数据、抽样比较方法及评价指标

文中使用了6组二分类非平衡数据来检验各种抽样方法的效果。数据来自UCI标准数据集,样本特征数范围是7-34,多数类与少数类的样本比从1.79到11.59(如表1所示)。设多数类和少数类样本量分别为M,m。少数类样本随机分为样本量均为m/2的子集,一组用于训练,一组用于测试;多数类样本随机分为两个子集,一个样本量为m/2的子集用于测试,另一个样本量为M-m/2的子集用于训练。采用各种抽样方法从用于训练的多数类子集中抽取m/2个样本用于训练,将少数类训练集和抽样后的多数类训练集合并为最终训练集,给定模型在此训练集上训练,并在两个样本量相同的测试集上进行测试,得到测试误差。每个实验重复10次,误差取平均值进行统计。

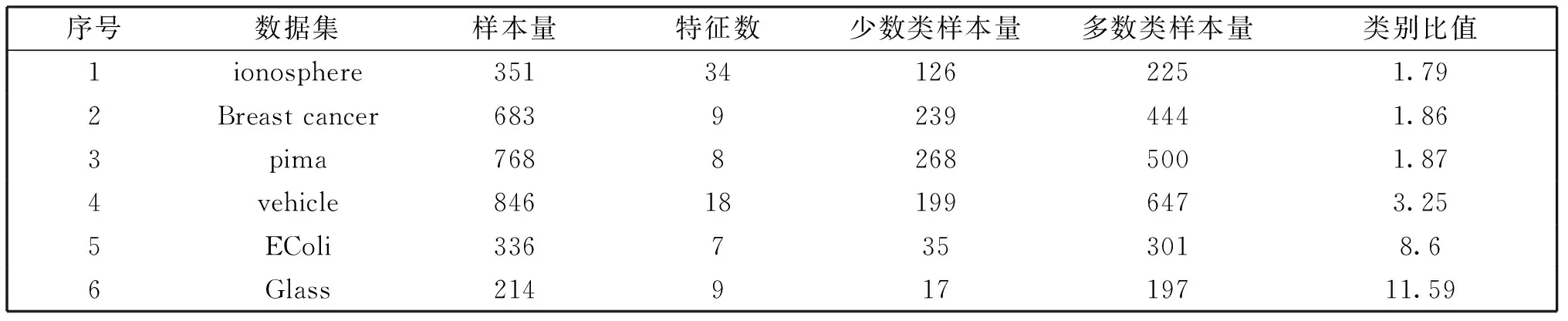
表1 实验用到的数据集

实验将无抽样数据分类结果作为参照,比较了9种抽样方法的效果,包括基本的随机欠抽样(RS)、四种常用的非平衡抽样方法(NM-1、NM-2、MD、CBS)、三种经典的抽样方法(KS、DPS-1、DPS-2)以及本文所提出的RRS方法。分类算法采用Libsvm工具箱,核函数是高斯核。

模型误差度量主要采用灵敏度、特异度、准确度和G-means进行综合评价。

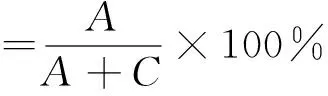
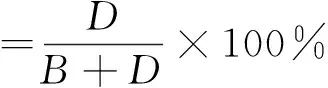
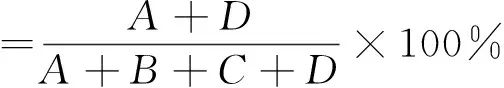
其中,A、B、C、D定义如表2所示。

表2 分类结果标识

(2)结果分析

表3列出了上述10种方法分类后的灵敏度、特异度和准确度比较。从表3可以看出,无抽样分类结果的灵敏度在除第2组数据的其它五组数据上都是最大,表明采用原始数据可以得到较好的分类灵敏度。RRS方法的灵敏度在第2组数据上最大,其他组数据上排名都仅次于无抽样分类方法。而无抽样分类结果的特异度在各组数据上都是最低,充分说明了抽样的必要性。

特异度在几个方法上都可能达到最大,而且RRS方法的特异度在两个数据集上都是最大,在其他四个数据集上与最大值比较接近。

关键的准确度指标的最大值均为RRS方法,其准确度排名均为第一。可见,RRS能够较好地兼顾多数类和少数类的分类准确性。

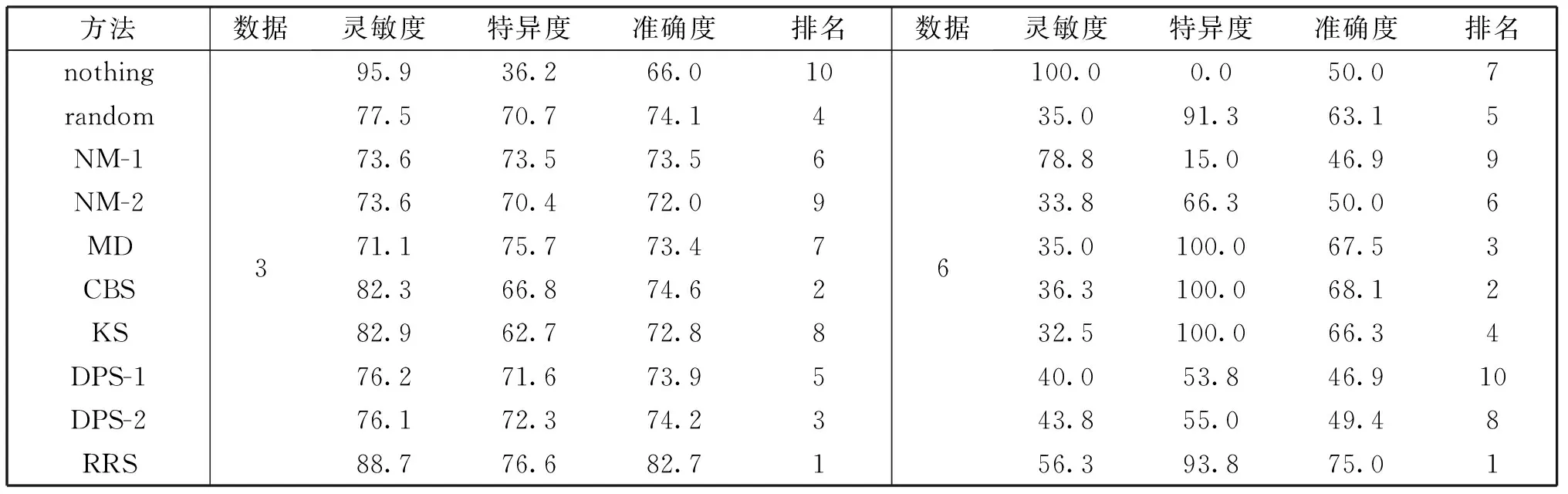
续表3 分类结果比较

图2对比了各种方法的G-means值。从图中可以看出,无抽样方法的G-means值在后五组数据均为最低,其中最后两组数据对应的值为零。可见在分类精度较低的情况下,无抽样的G-means更能体现抽样方法的作用。RRS的G-means在所有数据上均为最大。在前两组数据上模型的分类精度较高,G-means值较大,RRS方法略优于其他方法;在后面四组数据上模型分类效果较差,这时RRS的G-means值相比于其他方法有明显提升。除CBS和KS方法外,其他方法均有G-means值过低的表现。如random、NM-1和NM-2在数据5、6,MD在数据4,DPS-1和DPS-2在数据6。从G-means角度来看,CBS和KS是仅次于RRS的相对稳定的欠抽样方法。

Fig.2 G-means图2 G-means

4 结论

针对非平衡数据分类问题,将KS抽样和DPS方法用于欠抽样。主要提出了去冗余抽样,可以兼顾样本的冗余程度和多数类样本的整体分布,尽量去除对分类结果影响不大的样本,从而有效降低样本的非平衡以及样本分布变化所产生的不利影响。实验结果表明,本文提出的方法对非平衡数据的分类结果明显优于其他方法,有效提高了少数类样本的判别精度。

RRS为多类非平衡数据的抽样提供了有益的参考。另外,在大数据背景下如何利用本文提出的抽样方法实现数据的近似同分布压缩是我们未来的工作。

[1]HeH,GarciaEA.LearningfromImbalancedData[J].IEEETransactionsonKnowledgeandDataEngineering,2009,21(9):1263-1284.DOI:10.1109/TKDE.2008.239.

[2] Chan P K,Stolfo S J.Toward Scalable Learning with Non-Uniform Class and Cost Distributions:A Case Study in Credit Card Fraud Detection[C]∥KDD.1998,98:164-168.

[3] Japkowicz N,Stephen S.The Class Imbalance Problem:A Systematic Study[J].IntelligentDataAnalysis,2002,6(5):429-449.

[4] Abe N.Invited Talk:Sampling Approaches to Learning from Imbalanced Datasets:Active Learning,Cost Sensitive Learning and Beyond[C]∥Proc.of ICML Workshop:Learning from Imbalanced Data Sets，2003,22.

[5] 邢胜,王熙照,王晓兰.基于多类重采样的非平衡数据极速学习机集成学习[J].南京大学学报自然科学,2016,52(1):203-211.

[6] Estabrooks A,Jo T,Japkowicz N.A Multiple Resampling Method for Learning from Imbalanced Data Sets[J].ComputationalIntelligence,2004,20(1):18-36.

[7] Laurikkala J.Improving Identification of Difficult Small Classes by Balancing Class Distribution[C]∥Conference on Artificial Intelligence in Medicine in Europe.Springer Berlin Heidelberg,2001:63-66.

[8] Elkan C.The Foundations of Cost-sensitive Learning[C]∥International Joint Conference on Artificial Intelligence.Lawrence Erlbaum Associates Ltd,2001,17(1):973-978.

[9] Ting K M.An Instance-weighting Method to Induce Cost-sensitive Trees[J].IEEETransactionsonKnowledgeandDataEngineering,2002,14(3):659-665.

[10] Mani I,Zhang I.kNN Approach to Unbalanced Data Distributions:A Case Study Involving Information Extraction[C]∥Proceedings of Workshop on Learning from Imbalanced Datasets，2003.

[11] Chawla N V,Bowyer K W,Hall L O,etal.SMOTE:Synthetic Minority Over-sampling Technique[J].JournalofArtificialIntelligenceResearch,2002,16:321-357.[12] Han H,Wang W Y,Mao B H.Borderline-SMOTE:A New Over-sampling Method in Imbalanced Data Sets Learning[C]∥International Conference on Intelligent Computing.Springer Berlin Heidelberg,2005:878-887.

[13] Batista G E,Prati R C,Monard M C.A Study of the Behavior of Several Methods for Balancing Machine Learning Training Data[J].ACMSigkddExplorationsNewsletter,2004,6(1):20-29.

[14] Chawla N V,Lazarevic A,Hall L O,etal.SMOTEBoost:Improving Prediction of the Minority Class in Boosting[C]∥European Conference on Principles of Data Mining and Knowledge Discovery.Springer Berlin Heidelberg,2003:107-119.

[15] Liu X Y,Wu J,Zhou Z H.Exploratory Undersampling for Class-imbalance Learning[J].IEEE Transactions on Systems,Man,and Cybernetics,Part B (Cybernetics),2009,39(2):539-550.DOI:10.1109/TSMCB.2008.2007853.

[16] 郭虎升,亓慧,王文剑.处理非平衡数据的粒度SVM学习算法[J].计算机工程,2010,36(2):181-183.

[17] Jo T,Japkowicz N.Class Imbalances Versus Small Disjuncts[J].ACMSigkddExplorationsNewsletter,2004,6(1):40-49.

[18] Rajer-Kanducˇ K,Zupan J,Majcen N.Separation of Data on the Training and Test Set for Modelling:A Case Study for Modelling of Five Colour Properties of a White Pigment[J].ChemometricsandIntelligentLaboratorySystems,2003,65(2):221-229.

[19] Galvao R K H,Araujo M C U,Jose G E,etal.A Method for Calibration and Validation Subset Partitioning[J].Talanta,2005,67(4):736-740.

[20] Budka M,Gabrys B.Density-preserving Sampling:Robust and Efficient Alternative to Cross-validation for Error Estimation[J].IEEETransactionsonNeuralNetworksandLearningSystems,2013,24(1):22-34.DOI:10.1109/TNNLS.2012.2222925.[21] Frank A,Asuncion A.UCI Machine Learning Repository,University of California,School of Information and Computer Science,Irvine,CA,2010.http:∥archive.ics.uci.edu/ml/.

An Imbalanced Data Classification Approach Based on Redundancy-removed Sampling

SHI Ying1,QI Hui2

(1.Office of Science and Technology, Taiyuan Normal University, Jinzhong 030619,China;2.Department of Computer, Taiyuan Normal University, Jinzhong 030619,China)

Under-sampling is a common technique for classifying on imbalanced data.Traditional sampling methods (like Kennard-Stonesampling and density-preserving sampling) aim to keep the distribution of dataset. Existing under-sampling methods usually choose samples around the boundary whose distribution may be different with the original distribution，and the results may become worse. We proposed a redundancy about data, i.e., if a sample belonging to majority class lies in the dense area and is far away from the boundary or samples belonging to minority class, it has large redundancy. Redundancy-removed sampling (RRS) deletes samples with large redundancy in the same way with classical sampling methods. The subset obtained by RRS will refain samples which are valuable for classification but with the same distribution. Meanwhile, the amounts of the two class samples become balanced. The experimental results demonstrate that the accuracy by RRS is higher than those by other sampling approaches especially for the datasets with low classification accuracy. In addition,the accuracy of minority class is also improved.

imbalanced data;classification;sampling method;redundancy-removed sampling

10.13451/j.cnki.shanxi.univ(nat.sci.).2017.02.001

2016-10-25；

2016-11-25

山西省青年科学基金(201601D202040)

史颖(1990-),女,山西长治人,硕士,助教,主要从事图像处理,机器学习,三维重建等方面的研究。E-mail:wshsy123@126.com

TP301

A

0253-2395(2017)02-0255-07