电流退火及长度对玻璃包裹丝GMI效应的影响
2017-05-25蒋申骏潘海林赵振杰
蒋申骏,潘海林,赵振杰
(华东师范大学物理与材料科学学院,上海200062)
电流退火及长度对玻璃包裹丝GMI效应的影响
蒋申骏,潘海林,赵振杰
(华东师范大学物理与材料科学学院,上海200062)
采用高频感应加热熔融快淬法制备了Fe73.5Cu1.0Nb3.0Si13.5B9非晶玻璃包裹丝.首先对制备态包裹丝进行电流退火,结果发现电流密度为4.2×107A/m2时,退火得到的玻璃包裹丝性能最佳,原因是此时有合适的纳米晶体积比例.进而研究了长度对其磁性和巨磁阻抗效应的影响.结果表明,随着长度的减小,微丝的各项异性场增大,磁阻抗比减小.采用退磁场模型给予了合理解释.
巨磁阻抗;电流退火;玻璃包裹丝;长度
0 引言
巨磁阻抗(Giant Magneto Impedance,GMI)效应是指铁磁材料的交流阻抗在外加磁场作用下发生显著变化的现象[1].GMI效应温度稳定性好,以其为原理研制的器件具有低功耗、磁滞小、灵敏度高等特点,使得在磁敏传感器等领域有巨大的应用价值[2].GMI效应的大小、曲线形状等特性是外加直流磁场、交变磁化驱动场和铁磁材料本身的磁结构三者共同作用的结果.
采用高频感应熔融拉丝法制备的玻璃包裹微丝,由直径为0.2~100µm金属芯和厚度0.2~20µm的玻璃层组成,这是制作GMI传感器的理想材料之一[3].与传统喷丝法制备的微丝相比,玻璃包裹丝的尺寸要小一个量级,同时具有良好的软磁性能和抗腐蚀性能,适合做小型化敏感元件.在拉丝过程中,微丝经过急冷处理,由于玻璃和金属具有不同的热胀系数,使玻璃包裹丝内存在一定的内应力,影响了微丝的软磁性能[4].可以通过去除玻璃层[5]或者适当的退火[6-7]处理来减少内应力,改善微丝的内部磁结构,从而提高环向磁导率和GMI效应.其中,电流退火操作简单,同时电流感应的磁场可以改善材料的磁结构,进而提高材料的GMI效应,常见于Co基非晶材料退火研究[7].而对于非晶Fe73.5Cu1.0Nb3.0Si13.5B9材料大都采用真空或者保护气氛下退火,在退火温度为480◦C时开始长出α-FeSi纳米晶粒,在退火温度为540~570◦C范围内长出适当体积比例的纳米晶粒,提高了软磁性能和GMI效应[8].仅少量研究工作涉及非晶条带的电流退火[9],鲜有对Fe基玻璃包裹丝的电流退火研究.
另外,软磁材料作为GMI磁敏传感器的敏感元件时,其长度是一个重要的参数,不仅涉及器件的功耗和体积大小,还直接涉及传感器的磁响应特性.
本文对非晶Fe73.5Cu1.0Nb3.0Si13.5B9玻璃包裹丝进行电流退火处理,得到了性能优异的纳米晶玻璃包裹丝,并研究分析了Fe73.5Cu1.0Nb3.0Si13.5B9纳米晶玻璃包裹丝长度对其GMI效应的影响.
1 实验
采用Taylor-Ulitovsky[10]法制备Fe73.5Cu1.0Nb3.0Si13.5B9玻璃包裹丝,总直径为21.50µm,玻璃层厚度为1.65µm的微丝.选取若干根长度为1.0 cm的微丝,用细砂纸去除其两端的玻璃层后夹在自制的夹子上,再用Agilent U3606A型直流电源,向夹子通入电流进行电流退火处理,电流密度范围为2.1×107~7.0×107A/m2,退火时间为180 s.对一根较长的微丝在4.2×107A/m2的电流密度下退火,再将其分成长度为0.5 cm、1.0 cm、2.0 cm、3.0 cm的微丝,利用Agilent4294A型精密阻抗分析仪测量微丝的GMI效应,测试频率范围为1~100 MHz.GMI比值定义为
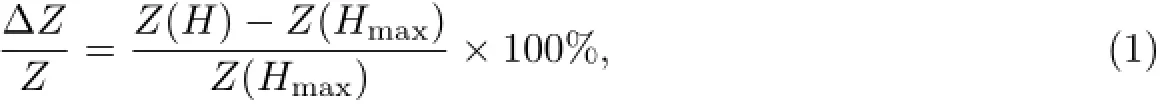
其中,Z(H)是不同外磁场下的阻抗值,外磁场由亥姆赫兹线圈产生,磁场范围为0~7 960 A/m,Z(Hmax)为最大磁场下的阻抗值,测量时外磁场平行于细丝长轴方向且与地磁场垂直以减小地磁场的影响.
2 结果与讨论
图1为不同电流密度退火后Fe73.5Cu1.0Nb3.0Si13.5B9玻璃包裹丝的GMI频谱图.从图中可以发现,随着退火电流密度的增加,磁阻抗先增加后减小.为了更加清楚了解电流退火对玻璃包裹丝巨磁阻抗的影响,图1插图给出了最大磁阻抗比随退火电流密度的关系曲线.从插图中可以看出退火过程分为3部分∶首先,当电流密度较小时,随着退火电流密度的增加,最大阻抗比先缓慢增加,这是因为电流产生焦耳热,有效地释放了部分内应力,提高了GMI效应;随后继续增加电流密度,最大阻抗比迅速增加,这说明微丝的温度进一步上升使得内部开始长出纳米晶[11],降低了磁致伸缩系数λs,同时较大的退火电流产生的环向磁场使得磁矩重新排列,更多的磁矩转到环向,相应的环向磁导率变大,阻抗比也随之变大,当电流密度为4.2×107A/m2时,微丝内部达到合适纳米晶体积比例,阻抗比达到最大,对应的真空退火温度在530~560◦C范围内[9];进一步增加电流密度,温度进一步升高,使得微丝内部开始出现Fe-B硬磁相[12],导致GMI效应急剧降低.

图1 不同电流密度退火后的Fe基玻璃包裹丝的GMI频谱图Fig.1 Frequency dependence of maximum magnetimpedance ratio with different annealing current densities
图2 为不同电流密度退火的玻璃包裹丝在30 MHz频率下的GMI曲线,为了能清楚看出微丝低磁场下的阻抗变化,磁场轴只取到800 A/m.从图中可以看出,退火后微丝的阻抗比都是随着外磁场的增加先增大再减小,表明微丝内部的磁畴结构发生变化,出现了环向磁结构.为了进一步反映微丝阻抗比随外磁场变化的快慢,采用GMI曲线中的斜率,定义巨磁阻抗效应的灵敏度S为

图2中的插图为灵敏度与电流密度的关系,可以发现随着电流密度的增加,微丝的灵敏度增大,当电流密度为4.2×107A/m2时,灵敏度达到最大值,阻抗比随外磁场的变化最明显,表明在电流的焦耳热和环向磁场的共同作用下,微丝内大部分磁矩趋近于环向,此时的磁结构为偏环向.
通过上面的分析,发现电流退火后的铁基玻璃包裹丝的GMI效应与真空退火的结果相当,因此有理由相信经过电流密度为4.2×107A/m2的电流退火后可以得到Fe73.5Cu1.0Nb3.0Si13.5B9纳米晶玻璃包裹丝,并且电流诱导出偏环向的磁结构.
图3为不同长度Fe73.5Cu1.0Nb3.0Si13.5B9纳米晶玻璃包裹丝的GMI频谱图.从图中可以看出,随着玻璃包裹丝长度的减小,最大阻抗比值减小,以及其对应的特征频率Fmax增大.特征频率的变化是由趋肤效应[13]决定的,玻璃包裹丝的趋肤深度δm大小为

其中,ω为交流电流的频率,µφ和σ分别为微丝的动态环向磁导率和电导率.
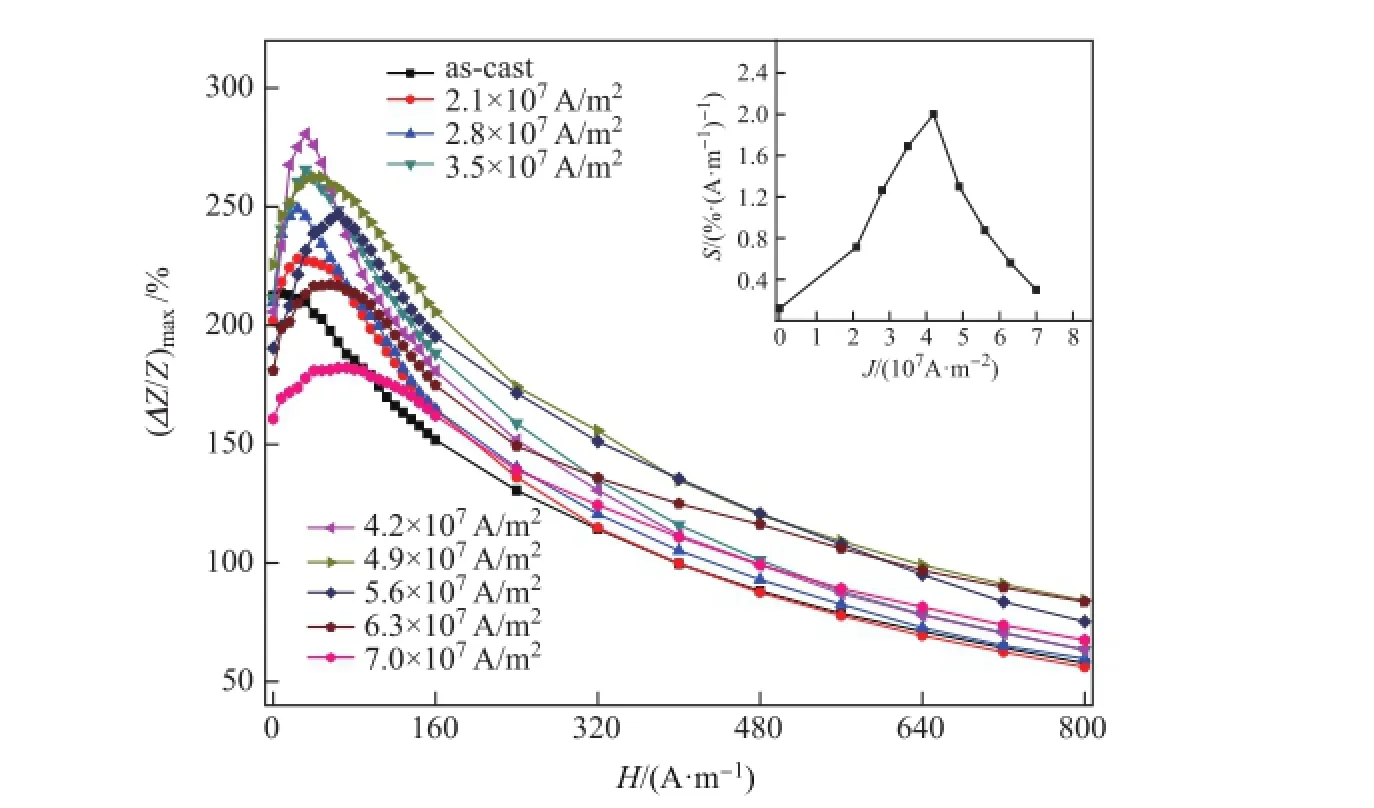
图2 不同电流密度退火的玻璃包裹丝在30 MHz频率下的GMI曲线Fig.2 Field dependence of magnetimpedance ratio with different annealing current densities at 30 MHz

图3 不同长度Fe基玻璃包裹丝的GMI频谱图Fig.3 Frequency dependence of maximum GMI ratio for microwires with different lengths
一般认为,微丝在某一起始频率时出现趋肤效应时,GMI效应开始显现;而在饱和磁场时,还能具有趋肤效应的频率为特征频率,且深度等于玻璃包裹丝的半径α时,可由式(3)得出饱和磁场下的环向磁导率µφ(Hsat)与特征频率fmax的关系,其表达式为

结合图3和关系式(4)可知,随着微丝长度减小,特征频率fmax增加,饱和磁场时的环向磁导率减小.
为了进一步的解释长度对GMI效应的影响,图4所示给出了不同长度玻璃包裹丝在30 MHz频率下的GMI曲线.从图中看出随着长度的减小,玻璃包裹丝的阻抗比减小,各向异性场HP从15.92 A/m增加到79.60 A/m.这可用图5所示的退磁场模型[14]来解释,图中Hk为各向异性场,HD为3 cm长时的退磁场,Hk和HD合成后的矢量和HP是玻璃包裹丝的有效各向异性场.随着长度的减小,退磁场HD增大至H′D,使得矢量和HP增大到H′P,并偏离玻璃包裹丝的环向,转向丝的轴向,使环向磁导率减小,导致GMI效应降低.图4中的插图为30 MHz频率下微丝的灵敏度与其长度的关系,从中可以看出长度越长,灵敏度也越大,表明阻抗比随外磁场的变化越明显,微丝内的磁矩越趋近于环向,这和退磁场模型得出的结果一致.
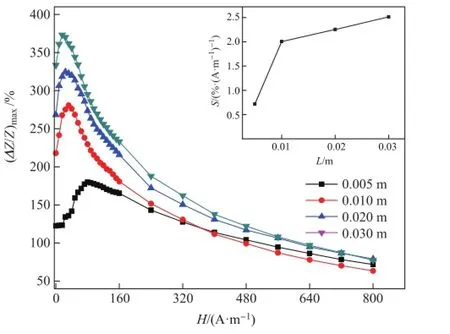
图4 不同长度的玻璃包裹丝在30 MHz频率下的GMI曲线Fig.4 Field dependence of magnetimpedance ratio with different lengths at 30 MHz
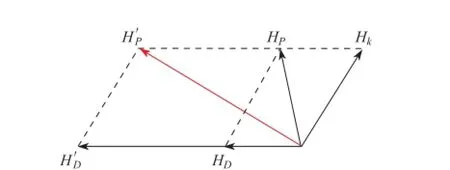
图5 退磁场产生影响的模型Fig.5 The model of demagnetizing field
3 结论
通过对非晶Fe73.5Cu1.0Nb3.0Si13.5B9玻璃包裹丝进行适当的电流退火后,可以释放其中部分内应力和生长出合适体积比例的纳米晶,从而得到性能较好的铁基纳米晶玻璃包裹丝.同时研究了长度对于纳米晶玻璃包裹丝巨磁阻抗效应的影响,发现随着微丝长度变短,各向异性场增大,相应的巨磁阻抗效应变差,通过退磁场模型进行了合理的解释.这对Fe73.5Cu1.0Nb3.0Si13.5B9纳米晶玻璃包裹丝作为传感器的敏感元件在如何选择长度上具有一定的参考价值.
[1]PHAN M H,PENG H X.Giant magnetoimpedance materials:Fundamentals and applications[J].Progress in Materials Science,2008,53(2):323-420.
[2]蒋颜玮,房建成,黄学功,等.巨磁阻抗传感器敏感材料的选择[J].功能材料,2009,40(1):1-6.
[3]CHIRIAC H,´OV´ARI T A.Amorphous glass-covered magnetic wires:preparation,properties,applications[J]. Progress in Materials Science,1996,40(5):333-407.
[4]ZHUKOVA V,LARIN V S,ZHUKOV A.Stress induced magnetic anisotropy and giant magnetoimpedance in Fe-rich glasscoated magnetic microwires[J].Journal of Applied Physics,2003,94(2):1115-1118.
[5]ZHUKAVA V,UMNOV P,MOLOKANOV V,et al.Magnetic properties and giant magneto-impedance ef f ect of ductile amorphous microwires without glass coating[J].Sensor Letters,2012,10(3-4):731-735.
[6]ZHUKOV V,CHURYUKABOVA M,KALOSHKIN S,et al.Ef f ect of annealing on magnetic properties and magnetostriction coefficient of Fe-Ni-based amorphous microwire[J].Journal of Alloys and Compounds,2015, 651(5):718-723.
[7]LIU J S,QIN F X,CHEN D M,et al.Combined current-modulation annealing induced enhancement of giant magnetoimpedance ef f ect of Co-rich amorphous microwires[J].Journal of Applied Physics,2014,115(17):3261-3263.
[8]TLAAT A,ZHUKOVA V,IPATOV M,et al.Optimization of the giant magnetoimpedance ef f ect of f i nemet-type microwires through the nanocrystallization[J].Journal of Applied Physics,2014,115(17):3131-3133.
[9]ZENG L,CHEN G,GONG F F,et al.Magneto-impedance ef f ect in the tensile stress-annealed Fe-based nanocrystalline alloy[J].Journal of Magnetism and Magnetic Materials,2000,208(1-2):74-77.
[10]TAYLOR G F.A method of drawing metallic f i laments and a discussion of their properties and uses[J].Physical Review,1924,23(5):655-660.
[11]严密,彭晓领.磁学基础与磁性材料[M].杭州:浙江大学出版社,2006.
[12]TALAAT A,IPATOV M,ZHUKOVA V,et al.Giant magneto-impedance ef f ect in thin Finemet nanocrystalline microwires[J].Physica Status Solidi C,2014,11(5-6):1120-1124.
[13]PANIN L V,MOHRI K.Magneto-impedance ef f ect in amorphous wires[J].Applied Physics Letters,1994,65(9): 1189-1191.
[14]李欣,张清,阮建中,等.不同长度敏感元件的两种巨磁阻抗传感器传感性能研究[J].传感技术学报,2008,21(7):1147-1150.
(责任编辑:李艺)
Inf l uence of current annealing and length of microwires on GMI ef f ect
JIANG Shen-jun,PAN Hai-lin,ZHAO Zhen-jie
(School of Physics and Materials Science,East China Normal University, Shanghai200062,China)
AmorphousFe73.5Cu1.0Nb3.0Si13.5B9microwiresarepreparedbythe Taylor-Ulitovsky method.Then,the as-prepared microwires are annealed by cuurent annealing.The best performance microwires are obtained at annealing current density of 4.2×107A/m2because of the suitable volume ratio between nanocrystalline and amorphous phases.Inf l uence of length on giant magnetoimpedance ef f ect and magnetic properties for microwires is then investigated.The results show that anisotropy field increases and the GMI ratio descreases with decreased length of the wire.Demagnetizing field model gives a reasonable explanation.
giant magneto impedance(GMI);current annealing;microwires;length
O482.5
:A
10.3969/j.issn.1000-5641.2017.03.013
1000-5641(2017)03-0114-06
2016-04-27
国家自然科学基金(51302085;11574084;51572086)
蒋申骏,男,硕士研究生,研究方向为磁性材料.E-mail:365068180@qq.com.
赵振杰,男,教授,博士生导师,研究方向为磁性材料与器件.
E-mail:zjzhao@phy.ecnu.edu.cn.
