Four kinds of gradient representations of autonomous Birkhoffian systems
2017-05-25CUIJinchaoLIAOCuicuiMEIFengxiang
CUI Jin-chao,LIAO Cui-cui,MEI Feng-xiang
(1.School of Science,Jiangnan University,Wuxi Jiangsu214122,China; 2.School of Aerospace Engineering,Beijing Institute of Technology,Beijing100081,China)
Four kinds of gradient representations of autonomous Birkhoffian systems
CUI Jin-chao1,LIAO Cui-cui1,MEI Feng-xiang2
(1.School of Science,Jiangnan University,Wuxi Jiangsu214122,China; 2.School of Aerospace Engineering,Beijing Institute of Technology,Beijing100081,China)
In order to study the integration and the stability of autonomous Birkhoffian systems,we propose four kinds of gradient systems to represent the autonomous Birkhoffian systems.By analysing the relationship between the gradient systems and the Birkhoffian systems,we obtain the conditions that the Birkhoffian systems can be transformed into a kind of four gradient systems.Then,we use the properties of gradient system to investigate the problems of integration and stability of the Birkhoffian systems.Finally,we give some examples to illustrate the application of the theory.
Birkhoffian systems;gradient system;integration;stability
0 Introduction
In Ref.[1],the author pointed out that it is especially suitable to study the gradient systems by using of Lyapunov functions.More general linear-gradient system has already been put forward in Ref.[2].In addition to usual gradient system,there are three other kinds of gradient systems,i.e.,the skew-gradient system,the symmetric negative def i nite gradientsystem,and the semi-def i nite gradient system.Thus,there are four kinds of gradient systems, which have important values for us to study integral and stability of solution of the system. For the applications of gradient system on mechanical systems,there have been some results already,such as Refs.[3-8].Based on those researches,the paper mainly tries to transform an autonomous Birkhoffian system[9-10]into one of the four kinds of gradient systems with some conditions,and then use the properties of four kinds of gradient system to study the problems of integration and stability of the Birkhoffian systems.
1 Four kinds of gradient systems and Birkhof f’s equations
The differential equations of motion of the general gradient systems are
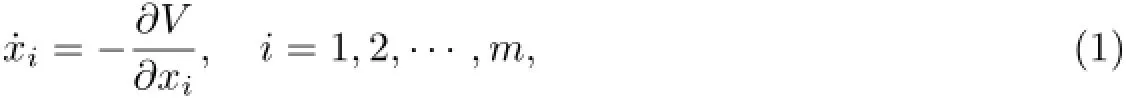
whereV(x)is called potential function andx=(x1,x2,···,xm).The general gradient systems consist of the following importance properties∶
1)The functionVis a Lyapunov function of the system(1)and˙V=0 if and only ifx=(x1,x2,···,xm)is an equilibrium point.
2)For the linear system of the gradient system(1),there are only real characteristic roots at any equilibrium points.
Similarly,the skew-gradient systems can be formula as
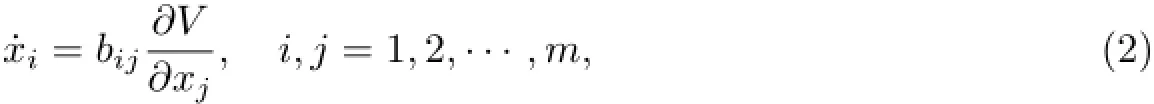
wherebij(x)=-bji(x)and the unified subscript denotes summation convention as well as in the following text.In addition,V=V(x)is called the energy function.The skew-gradient systems have the following importance properties∶
1)The functionV=V(x)is an integration of the system(2).
2)IfVis a Lyapunov function,the solution of the system(2)is stable.
The differential equations of the gradient systems with symmetric negative def i nite matrices are[2]
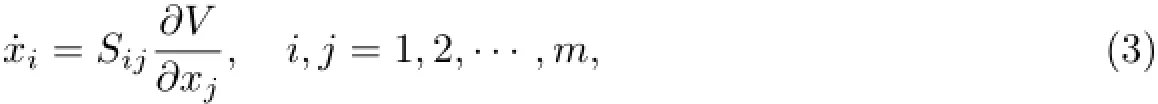
whereSij=Sij(x)is symmetric negative def i nite matrix.This system has the property as follows∶IfVis a Lyapunov function,the solution of the system(3)is stable.
The differential equations of the gradient systems with negative semi-def i nite matrices are[2]

whereaij=aij(x)is symmetric negative semi-def i nite matrix.The property of system(4)as follows∶ifVis a Lyapunov function,the solution of the system(4)is stable.
In order to convenience our statement,the above four kinds of gradient systems are separately called as the first to the fourth class gradient system.
2 The autonomous Birkhof f’s equations
The gradient representations of autonomous Birkhoffian systems have the form
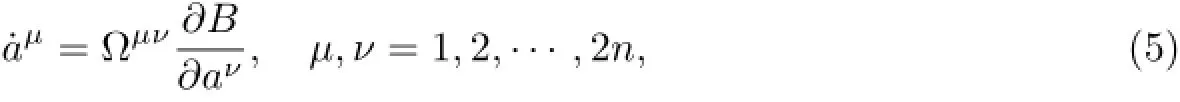
whereB=B(a),a=(a1,a2,···,a2n)and we have
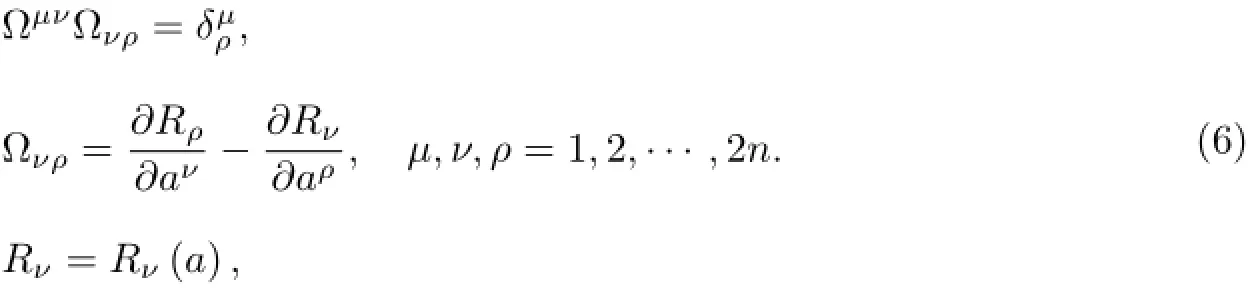
For the system(5),if there exist matrices(bµν(a)),(Sµν(a)),(aµν(a))and a functionV=V(a)satisfying the following conditions
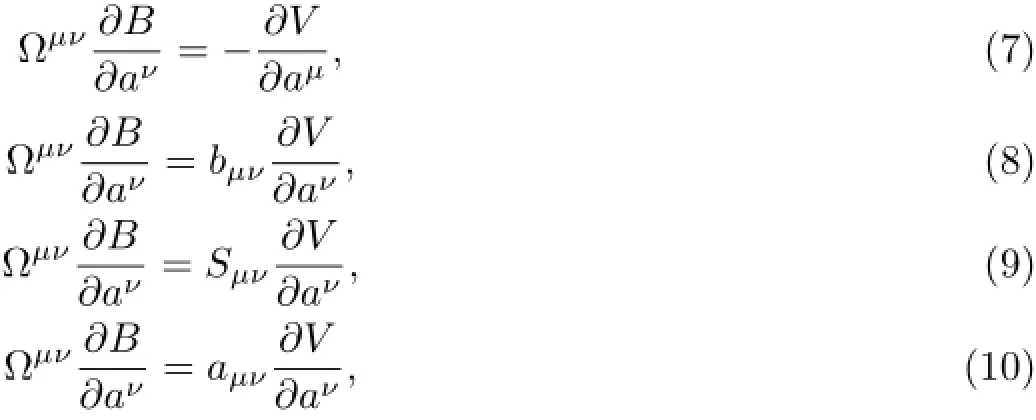
it can be transformed into one of the four kinds of gradient systems which be def i ned at the end of section 2.Clearly,Eq.(8)can be satisfied easily,but not the case of Eqs.(7),(9),and (10).
3 Illustrative examples
Consider a Birkhoffian system with[9]

Try to transform it into a gradient system and study the stability of solution. From the Birkhoffian equation(5),we know that

LetV=B,we have

which is the second kind of gradient system.Vis an integral of the system but cannot be a Lyapunov function.Consider the second and the fourth identities of the above equation and they can be rewritten as

where

which is not only an integral but also a Lyapunov function,therefore the solutionsa2=a4=0 are stable.
Birkhoffian system is
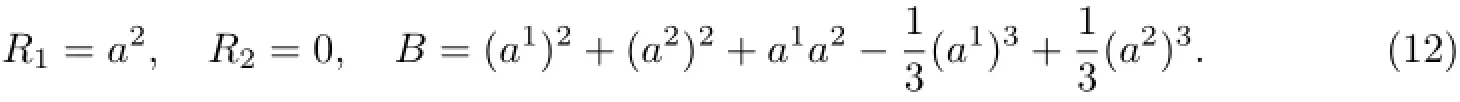
Try to transform it into a gradient system and study stability of solution.
From the Birkhoffian equation(5),we know that
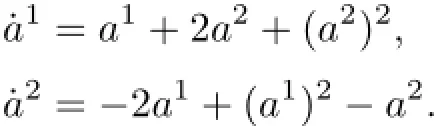
It can be rewritten as

where the matrix is anti-symmetric andVsatisfy
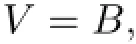
which is the second kind of gradient system.Vis an integral of the system and a Lyapunov function.Therefore,the solutionsa1=a2=0 are stable.
Birkhoffian system is
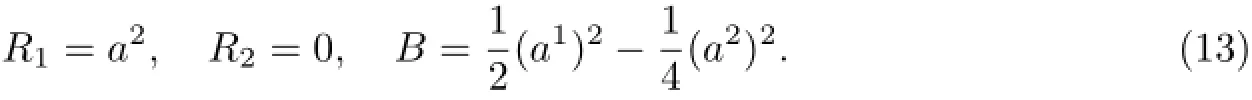
Try to transform it into a gradient system and study stability of solution.
The Birkhoffian equation(5)gives

or
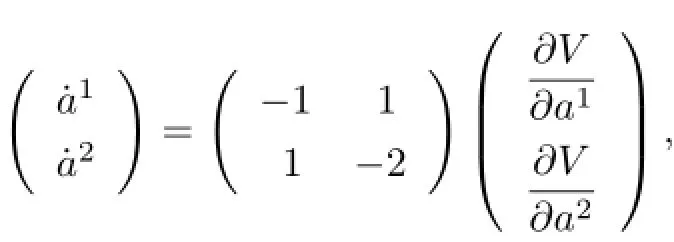
where the matrix is symmetric negative def i nite and V is
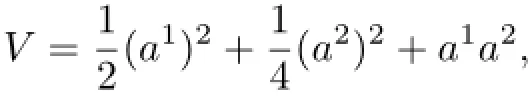
which is the third kind of gradient system.V is not a Lyapunov function.The characteristic equation has positive real roots.Therefore,the solutions a1=a2=0 are not stable.
4 Conclusions
We know that the autonomous Birkhoffian systems consist of the following properties,i.e., Birkhoffian function B is integral of the system,and if B can also be a Lyapunov function,the solutions of the system are stable,which is obtained in view of gradient system in this paper.It is easy to see that the autonomous Birkhoffian system is the second kind system naturally,but it is difficult to become three other kinds of gradient systems.Even through an autonomous Birkhoffian system can be transformed into three other kinds of gradient systems,V is also very difficult to become the Lyapunov function.In this case,the first-order approximation theory can be used if we want to study the stability of solution.
[1]HIRSCH M W,SMALE S,DEVANEY R L.differential Equations,Dynamical Systems,and an Introduction to Chaos[M].3rd ed.Waltham:Academic Press,2012.
[2]MCLACHLAN R I,QUISPEL G R W,ROBIDOUX N.Geometric integration using discrete gradients[J].Philosophical Transactions of the Royal Society of London:Series A,1999,357:1021-1045.
[3]LOU Z M,MEI F X.A second order gradient representation of mechanics system[J].Acta Physica Sinica,2012, 61:337-340.
[4]MEI F X.On the gradient system[J].Mechanics in Engineering,2012,34:89-90.
[5]MEI F X,WU H B.A gradient representation for generalized Birkhoffian system[J].Dynamics and Control, 2012,10:289-292.
[6]MEI F X,WU H B.Generalized Hamilton system and gradient system[J].Science China Physics,Mechanics and Astronomy,2013,43:538-540.
[7]MEI F X,CUI J C,WU H B.A gradient representation and a fractional gradient representation of Birkhof f system[J].Transactions of Beijing Institute of Technology,2012,32:1298-1300.
[8]MEI F X.Analytical MechanicsⅡ[M].Beijing:Beijing Institute of Technology Press,2013.
[9]GUO Y X,LIU C,LIU S X.Generalized Birkhoffian realization of nonholonomic systems[J].Communications in Mathematics,2010,18:21-35.
[10]SANTILLI R M.Foundations of Theoretical MechanicsⅡ[M].New York:Springer,1983.
(责任编辑:李艺)
自治Birkhoff系统的四类梯度表示
崔金超1,廖翠萃1,梅凤翔2
(1.江南大学理学院,江苏无锡214122;2.北京理工大学宇航学院,北京100081)
提出四类梯度系统,并研究自治Birkhof f系统的梯度表示.给出系统成为梯度表示和分数维梯度的条件,利用梯度系统的性质来研究Birkhof f系统的积分和解的稳定性,举例说明结果的应用.
Birkhof f系统;梯度系统;积分;稳定性
2016-04-19
国家自然科学基金(11272050,11401259);江南大学自主科研资助项目(JUSRP11530)
崔金超,男,讲师,研究方向为约束力学系统的稳定性.E-mail:cjcwx@163.com.
O316
A
10.3969/j.issn.1000-5641.2017.03.010
1000-5641(2017)03-0094-05
