微扰力系统一阶近似守恒量与对称性研究
2017-05-25楼智美
楼智美
(绍兴文理学院物理系,浙江绍兴312000)
微扰力系统一阶近似守恒量与对称性研究
楼智美
(绍兴文理学院物理系,浙江绍兴312000)
提出了用泊松括号求一阶近似守恒量的方法,将微扰力学系统的Hamilton函数看成是未受微扰作用系统的Hamilton函数和微扰项两部分组成.先根据未受微扰作用力学系统的特点选择一种合适的方法求得其精确守恒量,再利用泊松括号和偏微分方程的性质求得守恒量的一阶微扰项,最后根据Noether对称性、Lie对称性和Mei对称性性质,求得与一阶近似守恒量相应的一阶近似Noether对称性、近似Lie对称性和近似Mei对称性.研究了受微扰作用的二维各向同性谐振子的一阶近似守恒量和近似对称性,得到了系统的3个一阶近似守恒量及它们相应的一阶近似对称性.结果表明,与3个一阶近似守恒量相应的一阶近似对称性既是近似Noether对称性,又是近似Lie对称性,也是近似Mei对称性.
两自由度微扰力学系统;一阶近似守恒量;泊松括号法;一阶近似对称性
0 引言
许多力学系统因受微扰作用,使其Hamilton函数中含有微扰项,从而导致力学系统的力学性质发生变化,如守恒量中出会出现微扰项、一些精确守恒量不再存在、对称性出现破损、轨道稳定性受到影响等等.众所周知,力学系统的对称性与守恒量之间存在着密切的联系,同样地,微扰力学系统的近似对称性和近似守恒量间也存在着必然的联系,研究微扰力学系统的近似对称性和近似守恒量对于研究力学系统的特性以及得到方程的近似解十分重要.近年来关于微扰力学系统近似对称性和近似守恒量的研究已取得许多成果[1-13],文献[1-9]比较注重近似对称性理论的研究,而文献[10-12]则比较注重对称性理论的实际应用.目前,求近似守恒量的方法主要有3种∶方法一为近似Lie对称性法[1],其主要思路是引进近似的群无限小变换,微分方程在此变换下近似保持不变则为近似Lie对称性,所得的守恒量为近似Lie对称性守恒量.方法二为近似Noether对称性法[2],哈密顿作用量在此变换下近似保持不变则为近似Noether对称性,所得的守恒量为近似Noether对称性守恒量.近似Lie对称性法和近似Noether对称性统称为近似对称性理论法,在求近似守恒量中均要用到近似的群无限小变换,并需要解出近似的无限小生成元和规范函数,理论性强且计算过程比较繁复.方法三为直接积分法[13],这种方法是把微扰力学系统的运动微分方程视为未受微扰力学系统与微扰项的迭加,先根据未受微扰力学系统的特点选择较合适的方法求得未受微扰力学系统的精确守恒量,再考虑微扰项对精确守恒量的影响,最后根据近似守恒量的性质直接求得近似守恒量.本文提出了一种用泊松括号求一阶近似守恒量的方法,将微扰力学系统的Hamilton函数看成是两部分组成,即H=H0+εH1,其中,H0为未受微扰作用系统的Hamilton函数,εH1为Hamilton函数的一阶微扰项,先根据H0的形式选择合适的方法求得未受微扰作用的力学系统的精确守恒量,再利用泊松括号和偏微分方程的性质求得守恒量的一阶微扰项,最后根据Noether对称性、Lie对称性和Mei对称性性质,求得与一阶近似守恒量相应的一阶近似Noether对称性、近似Lie对称性和近似Mei对称性.本文以受微扰作用的二维各向同性谐振子为例,得到了3个一阶近似守恒量,并研究了其相应的一阶近似对称性.结果表明,与3个一阶近似守恒量相应的一阶近似对称性既是近似Noether对称性,又是近似Lie对称性,也是近似Mei对称性.
1 用泊松括号求一阶近似守恒量的基本理论
设二自由度微扰力学系统的Hamilton函数为
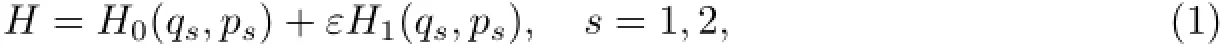
其中,ε≪1为微扰系数,H0为未受微扰作用的力学系统的Hamilton函数,H1为Hamilton函数的一阶微扰项系数.与系统(1)相应的Hamilton正则方程为

系统(1)的一阶近似守恒量可表示成

一阶近似守恒量的性质用泊松括号可表示成
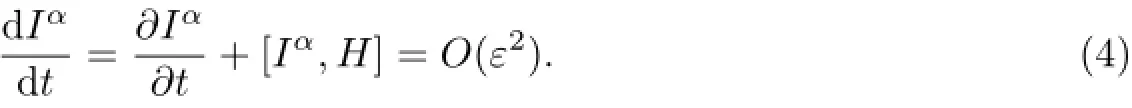
将式(1)、式(3)代入式(4),并利用精确守恒量的性质

忽略ε2项,可得应满足的条件为

展开式(6)得
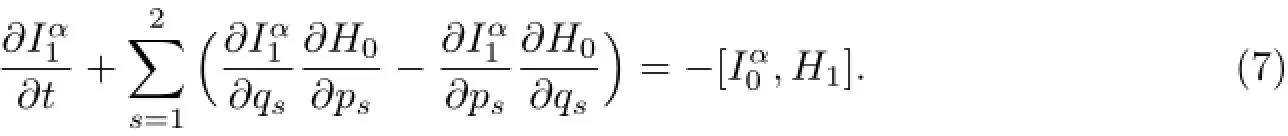
对于给定的微扰力学系统,H0(qs,ps),H1(qs,ps)是已知的,可以选择合适的方法求得,即式(7)中的偏微分方程.根据偏微分方程的特征方程

为讨论方便,本文假设微扰力学系统的Hamilton函数只含一阶微扰项,守恒量也只计算到一阶近似项,因此忽略了式(4)中的二阶近似项事实上,二阶近似不一定为0,只有当Hamilton函数的微扰项εH1和守恒量的微扰项都仅仅是广义坐标qs的函数或仅仅是广义动量ps的函数时,
2 一阶近似守恒量的3种近似对称性
与一阶近似守恒量相应的近似对称性可有3种,即近似Noether对称性、近似Lie对称性和近似Mei对称性.根据近似对称性理论[1-2],引进近似的群无限小变换

其中,δ为无限小参数,为与第α个一阶近似守恒量相对应的无限小变换生成元.式(9)的无限小生成元向量为
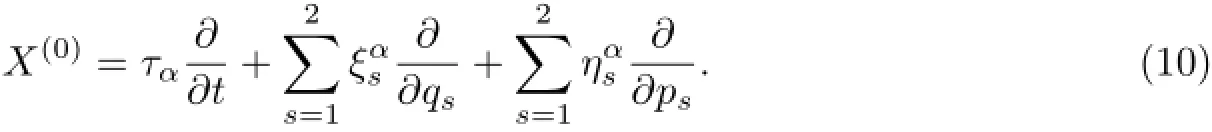
式(10)的一次扩展为

式(9)—式(11)中,
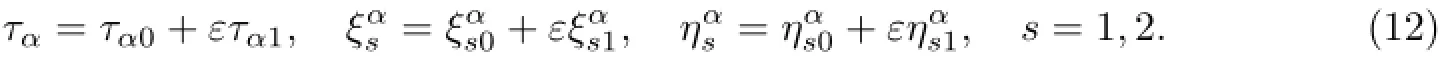
根据Hamilton系统的Noether逆定理[14],可以得到如下结论∶如果已知Hamilton系统的守恒量Iα,那么可由守恒量Iα找到相应的生成元使无限小变换(9)为系统的一阶近似Noether对称变换(或一阶近似Noether准对称变换),则系统具有一阶近似Noether对称性(或系统具有一阶近似Noether准对称性).
如果已知Hamilton系统的守恒量Iα和Hamilton函数,由

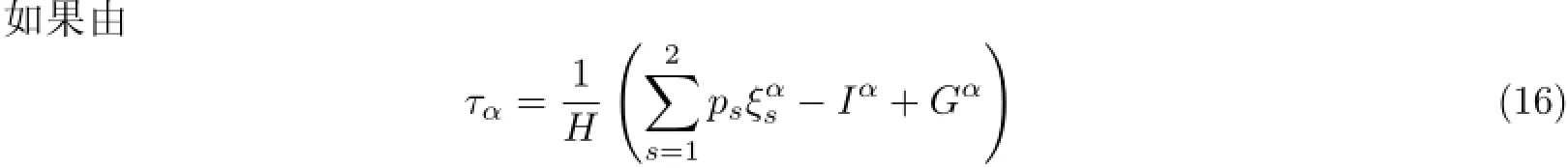
确定τα,其中为规范函数,且满足Noether恒等式
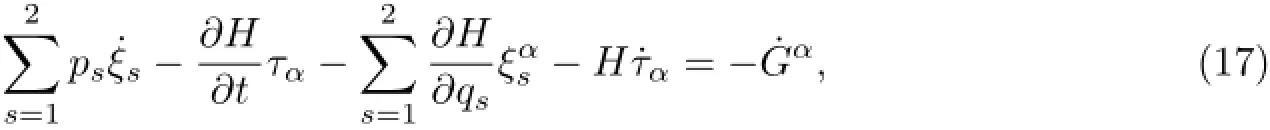
则由式(14)—式(16)确定的生成元τα,使无限小变换(9)为系统的一阶近似Noether准对称变换,则说明系统具有一阶近似Noether准对称性.
根据近似Lie对称性理论[1],可以得到如下结论∶如果由式(13)—式(15)或式(14)—式(16)确定的生成元τα,满足Lie对称性确定方程

其中gs,hs由式(2)确定,则与守恒量Iα相应的无限小变换(9)是一阶近似Lie对称变换,说明系统具有一阶近似Lie对称性.
根据Mei对称性理论[15],可以得到如下结论∶如果由式(13)—式(15)或式(14)—式(16)确定的生成元τα,满足Mei对称性判据方程

则与守恒量Iα相应的无限小变换(9)是一阶近似Mei对称变换,系统具有一阶近似Mei对称性.
3 应用举例
设二自由度微扰力学系统的Hamilton函数为
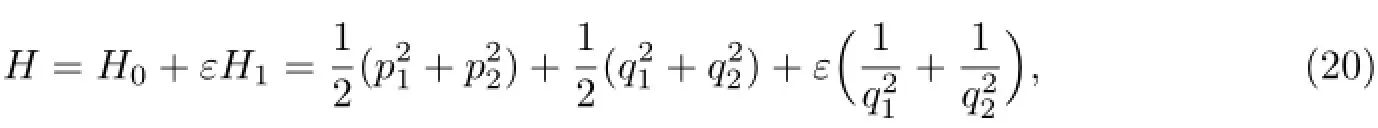
其中未受微扰作用力学系统的Hamilton函数为

Hamilton函数的一阶微扰项为

H0表示二维各向同性谐振子的Hamilton函数,可用多种方法求得其精确守恒量.文献[16]用Noether定理求得了二维各向同性谐振子系统的3个独立的守恒量

与式(20)相应的Hamilton正则方程为

将式(21)—式(23)代入式(7)得
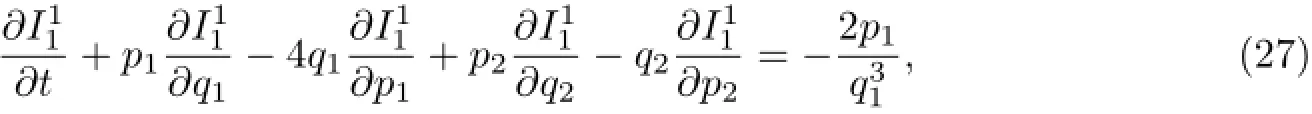
其特征方程为
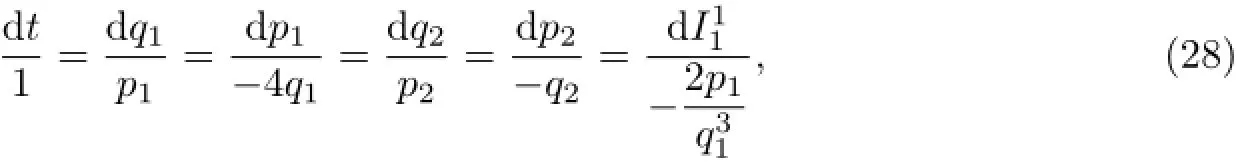
由其中的一个等式
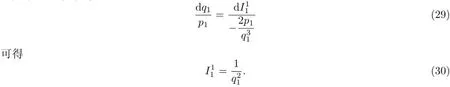
将式(21)—式(22)和式(24)代入式(7)得
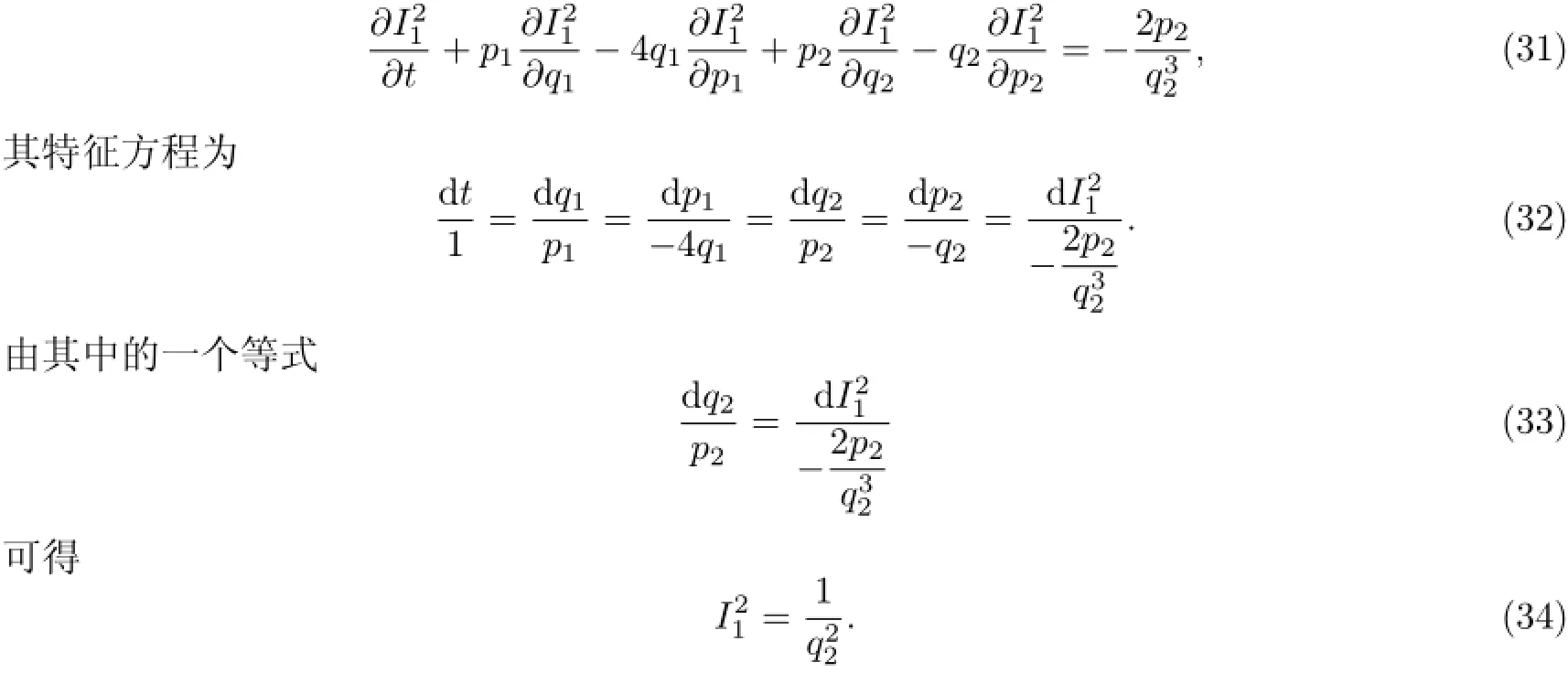
将式(21)—式(22)和式(25)代入式(7)得
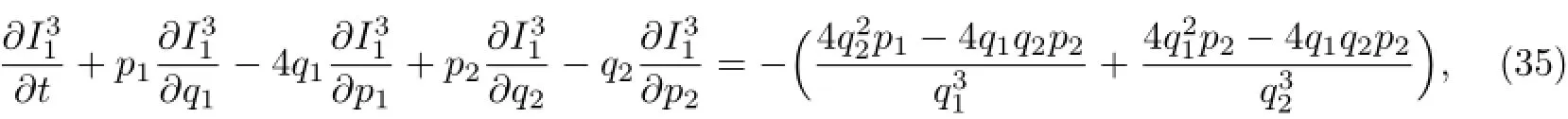
其特征方程为
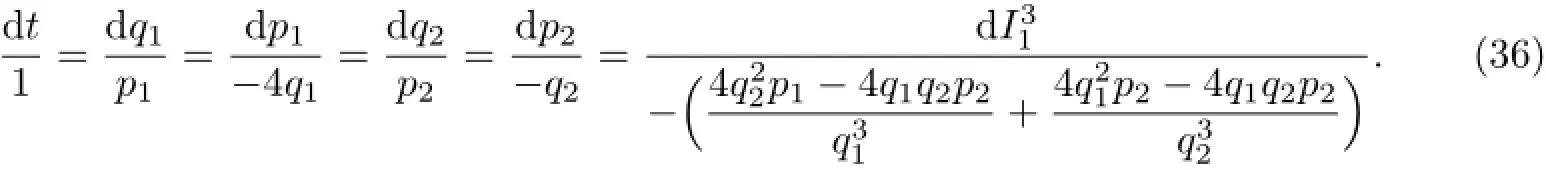
由其中的一个等式

可得

联合式(23)—式(25)和式(30)、式(34)、式(38),可得系统的3个一阶近似守恒量

很明显,由式(20)表示的Hamilton函数是可以分离变量的,可分离成I1,I2两部分,且满足I1+I2=H,这两部分均是守恒的.
下面讨论与一阶近似守恒量相对应的对称性.将式(39)—式(41)式依次代入式(13)—式(15),并考虑式(20),得不到τα的解析解,说明系统(20)不存在一阶近似Noether对称性.
将式(39)—式(41)依次代入式(14)—式(16),并考虑式(17)和式(20),可得到如下3组与一阶近似守恒量I1,I2,I3相对应的解,分别为
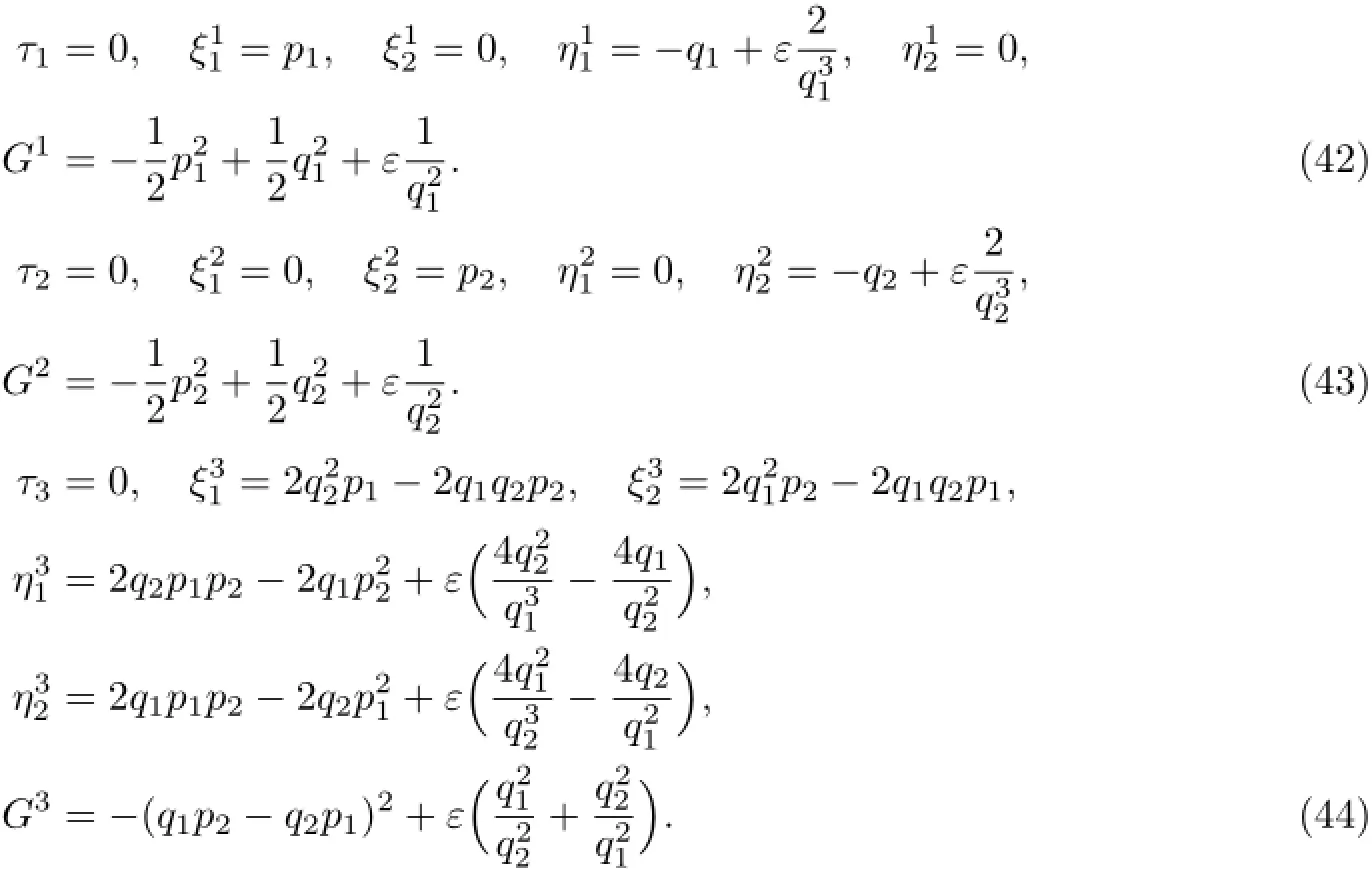
因此,由式(42)—式(44)表示的生成元τα,使无限小变换(9)为系统的一阶近似Noether准对称变换,系统具有一阶近似Noether准对称性.
下面讨论一阶近似守恒量的Lie对称性.经验证,由式(42)—式(44)表示的生成元τα,均满足Lie对称性确定方程式(18),说明由式(42)—式(44)表示的生成元τα,小变换(9)为系统的一阶近似Lie对称变换,系统具有一阶近似Lie对称性.
下面讨论一阶近似守恒量的Mei对称性.将式(42)—式(44)中的生成元及式(20)代入式(10)和Mei对称性判据方程式(19),可得

说明由式(42)—式(44)表示的生成元τα,使无限小变换(9)为系统的一阶近似Mei对称变换,系统具有一阶近似Mei对称性.
4 结论
本文提出了一种用泊松括号求一阶近似守恒量的方法,此方法的主要思路是将微扰力学系统的Hamilton函数看成是两部分组成,即H=H0+εH1,先选择合适的方法求得未受微扰作用系统(Hamilton函数为H0)的精确守恒量再用泊松括号和偏微分方程的性质求得守恒量的一阶微扰项,最后根据Noether对称性、Lie对称性和Mei对称性性质,求得与一阶近似守恒量相应的一阶近似Noether对称性、近似Lie对称性和近似Mei对称性.文中用上述方法求得了受微扰作用的二维各向同性谐振子的3个一阶近似守恒量,并得到与它们相应的一阶近似对称性,结果表明,与3个一阶近似守恒量相应的一阶近似对称性既是近似Noether对称性,又是近似Lie对称性,也是近似Mei对称性.用泊松括号法求近似守恒量方法思路清晰,物理意义明确,数学计算较近似对称性法简单,并易推广应用于求高阶微扰力学系统的高阶近似守恒量,这方面内容将在另文研究.
[1]LEACH P G L,MOYO S,COTSAKIS S,et al.Symmetry,singularities and integrability in complex dynamicsⅢ:Approximate symmetries and invariants[J].Journal of Nonlinear Mathematical Physics,2001,8(1):139-156.
[2]GOVINDER K S,HEIL T G,UZER T.Approximate Noether symmetries[J].Physics Letters A,1998,240(3): 127-131.
[3]NAEEM I,MAHOMED F M.Approximate first integrals for a system of two coupled van der Pol oscillators with linear dif f usive coupling[J].Mathematical and Computational Applications,2010,15(4):720-731.
[4]UNAL G.Approximate generalized symmetries,normal forms and approximate first integrals[J].Physics Letters A,2000,266(2):106-122.
[5]DOLAPIC I T,PAKDEMIRLI M.Approximate symmetries of creeping flow equations of a second grade f l uid [J].International Journal of Non-linear Mechanics,2004,39(10):1603-1619.
[6]KARA A H,MAHOMED F M,QADIR A.Approximate symmetries and conservation laws of the geodesic equations for the Schwarzschild metric[J].Nonlinear Dynamics,2008,51(1/2):183-188.
[7]GREBENEV V N,OBERLACK M.Approximate Lie symmetries of the Navier-Stokes equations[J].Journal of Non-linear Mathematical Physics,2007,14(2):157-163.
[8]JOHNPILLAI A G,KARA A H,MAHOMED F M.Approximate Noether-typesymmetries and conservation laws via partial Lagrangians for PDEs with a small parameter[J].Journal of Computational and Applied Mathematics, 2009,223(1):508-518.
[9]ZHANG Z Y,YONG X L,CHEN Y F.A new method to obtain approximate symmetry of nonlinear evolution equation form perturbations[J].Chinese Physics B,2009,18(7):2629-2633.
[10]楼智美.两自由度弱非线性耦合系统的一阶近似Lie对称性与近似守恒量[J].物理学报,2013,62(22):220202.
[11]楼智美,梅凤翔,陈子栋.弱非线性耦合二维各向异性谐振子的一阶近似Lie对称性与近似守恒量[J].物理学报,2012,61(11): 110204.
[12]楼智美.微扰Kepler系统轨道微分方程的近似Lie对称性与近似不变量[J].物理学报,2010,59(10):6764-6769.
[13]楼智美.含非线性微扰项的二阶动力学系统的一阶近似守恒量的一种新求法[J].物理学报,2014,63(6):060202.
[14]梅凤翔.李群和李代数对约束力学系统的应用[M].北京:科学出版社,1999:120-126.
[15]梅凤翔.约束力学系统的对称性与守恒量[M].北京:北京理工大学出版社,2004:10-14.
[16]楼智美.用Noether定理确定各向同性谐振子的守恒量[J].力学与实践2003,25(1):72-73.
(责任编辑:李艺)
The study of the first order approximate conserved quantities and approximate symmetries of perturbed mechanical system
LOU Zhi-mei
(Department of Physics,Shaoxing University,Shaoxing Zhejiang312000,China)
A Poisson bracket method to obtain the fi rst order approximate conserved quantities of two-dimensional perturbed mechanical system is proposed.We consider the perturbed Hamiltonian function as the combination of Hamiltonian function of unperturbed system and the perturbed term.First,according to the peculiarity of unperturbed system, we select a suitable method to obtain the exact conserved quantities of unperturbed system.Second,we calculate the fi rst order perturbed terms of conserved quantities by using Poisson bracket and the character of partial di ff erential equations.Finally,according to the characters of Noether symmetries,Lie symmetries and Mei symmetries,the fi rst order approximate Noether symmetries,approximate Lie symmetries and approximate Mei symmetries of the fi rst order approximate conserved quantities can be obtained.A perturbed two-dimensional isotropic harmonic oscillator is studied in this paper,and three fi rst order approximate conserved quantities are obtained by using Poisson bracket method, and the fi rst order approximate symmetries of three fi rst order approximate conservedquantities are either approximate Noether symmetries or approximate Lie symmetries and Mei symmetries.
two-dimensional perturbed mechanical system;first order approximate conserved quantities;Poisson bracket method;first order approximate symmetries
O316
A
10.3969/j.issn.1000-5641.2017.03.011
1000-5641(2017)03-0099-08
2016-04-01
国家自然科学基金(11472177)
楼智美,女,教授,主要从事分析力学研究.E-mail:louzhimei@usx.edu.cn.
