基于HJC模型的钢筋混凝土侵彻仿真失效准则与参数
2017-05-25徐建军杨晋伟张海良
林 琛,徐建军,杨晋伟,张海良
(1.中北大学机电工程学院,山西 太原 030051;2.淮海工业集团有限公司,山西 长治046000)
基于HJC模型的钢筋混凝土侵彻仿真失效准则与参数
林 琛1,徐建军1,杨晋伟2,张海良2
(1.中北大学机电工程学院,山西 太原 030051;2.淮海工业集团有限公司,山西 长治046000)
针对侵彻钢筋混凝土各种本构模型失效定义不够完善的问题,提出了基于HJC材料模型的钢筋混凝土侵彻仿真失效准则与参数的方法。该方法是基于HJC本构模型自带的失效准则定义,运用LSDYNA算法修正HJC材料模型中的失效控制参数FS,采用上述模型自带的失效准则与参数并联合其他三种辅助失效准则来弥补HJC材料模型在失效定义方面的不足。侵彻试验结果表明,该数值模拟方法产生的侵彻贯穿现象与试验结果基本相同,因此该数值模拟方法具有一定的工程价值。
HJC材料模型;侵彻;钢筋混凝土;数值模拟;单元失效准则
0 引言
钢筋混凝土的侵彻和贯穿问题涉及到弹靶的几何尺寸与结构、材料强度、应力波的传播、摩擦效应等诸多因素[1-2]。由于通过理论分析去获取解析解有相当程度的复杂性而实际靶场试验的成本高昂,且打靶测试的数据适用范围较窄,故而针对此类问题目前广泛运用数值模拟的方法。
数值模拟结果的准确性与钢筋混凝土的建模方法、混凝土材料动态本构模型及失效准则与参数等因素密切相关[3]。由于钢筋作为传统金属材料,其本构关系与损伤较为明确。近年来国内外对于数值模拟侵彻钢筋混凝土的失效准则与参数问题研究主要集中在混凝土材料动态本构模型关于失效的定义。文献[4]提出了TCK模型;文献[5]提出了RHT模型;文献[6]提出了HJC模型;文献[7]考虑了洛德角的影响得到改进MHJC模型;而马爱娥等[8]以TCK模型和HJC模型为基础,自定义了混合型损伤模型作为混凝土的本构模型。
虽然随着混凝土材料的动态本构模型不断改进,失效的定义得到不断的发展。但是由于钢筋混凝土在侵彻加载条件下的损伤具有高度的复杂性。上述各种本构模型失效定义仍无法模拟侵彻混凝土材料的全部失效形式。尤其是侵彻钢筋混凝土材料时需要特别考虑混凝土的骨料、孔洞等在结构中的随机性分布而造成对钢筋材料在冲击载荷作用下变形破坏。在这一方面HJC材料本构模型考虑得较为全面。
LSDYNA中的关键字*MAT_ADD_ERROSION提供了8种辅助单元失效准则,加上HJC模型中自带的失效准则与参数。故而HJC模型有更为丰富的失效准则可供选择。对于完善侵彻作用下钢筋混凝土关于失效的定义,究竟采用哪种辅助失效准则最为合适,目前没有定论。文献[9-10]采用最大静水压和最大剪应变失效准则综合控制, 模拟的结果在漏斗坑形成方面不明显。而文献[11-12]分别采用单一失效准则控制,其侵彻工况与现实试验工况偏差太远。且综合国内外已有的众多相关研究中鲜有关于其最后一个关键字参数FS的理论性的研究。
本文针对上述侵彻钢筋混凝土各种本构模型失效定义不够完善的问题,提出了基于HJC材料模型的钢筋混凝土侵彻仿真失效准则与参数的方法。
1 HJC本构模型
HJC材料模型,是由金属材料中广泛应用的JC(Johnson_Cook)模型发展而来,其特点是能够反映混凝土等脆性材料在大应变、高应变速率和高围压下及材料损伤失效的动态响应。
HJC本构模型主要包括三方面:状态方程、屈服面方程以及损伤演化方程,下面分别对各部分作简要介绍和分析。
1.1 状态方程
材料所受压力P与相应的应变μ的关系曲线如图1所示。

图1 HJC材料状态方程Fig.1 State equation of HJC
1.1.1 拉伸状态方程
1)线弹性阶段
P=Kμ
(1)

2)裂缝贯通断裂阶段
P=T(1-D)
(2)
式(2)中,T是材料最大拉伸截止静水压力,D是材料的损伤程度。
从图1可知即使此时拉应力不再变化然而应变却依旧缓慢增大,即可以看出该本构模型在拉伸失效描述与现实混凝土拉伸失效相比过于简单。
1.1.2 压缩状态方程
在该材料本构模型的压缩阶段又分为:线弹性阶段、过渡阶段和压实阶段。
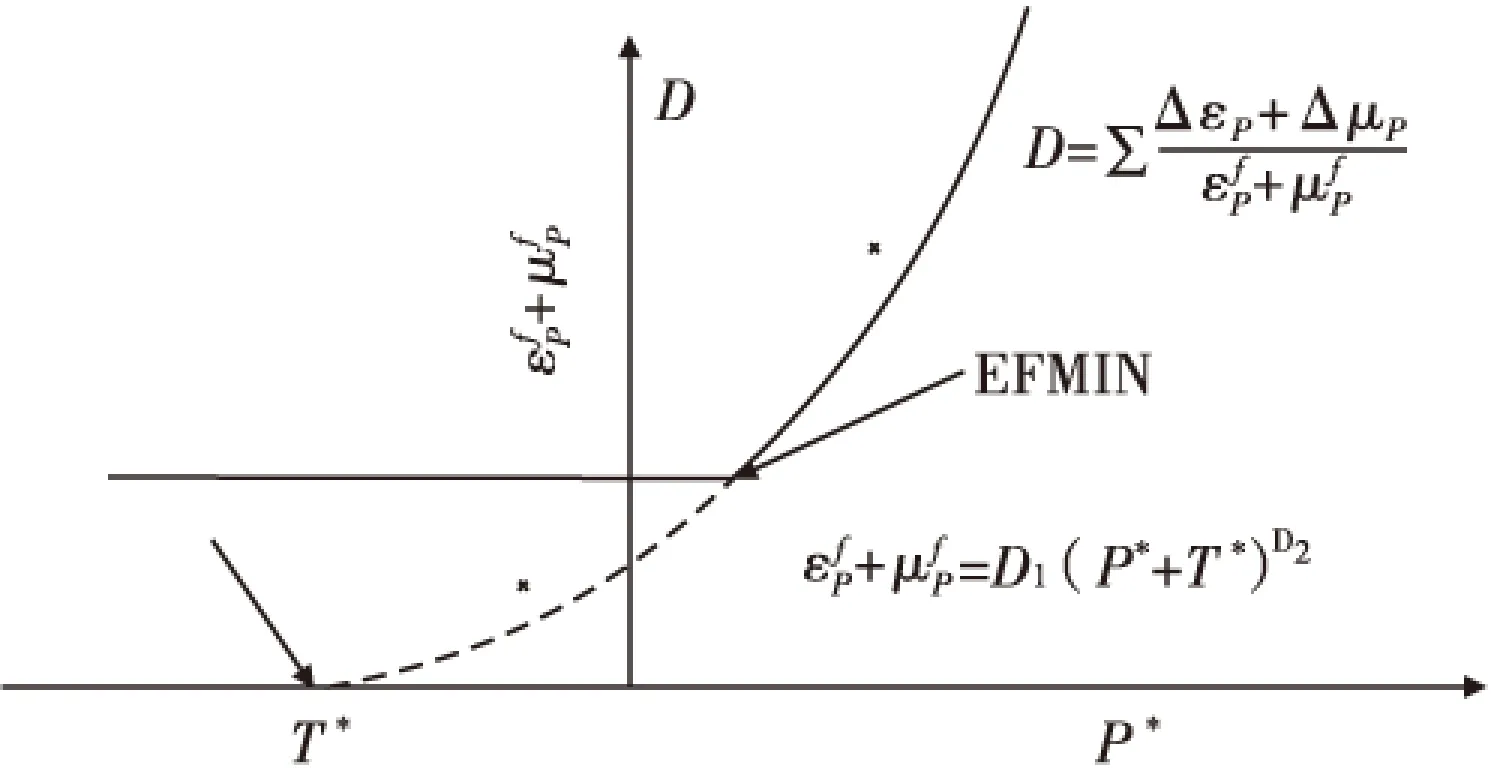
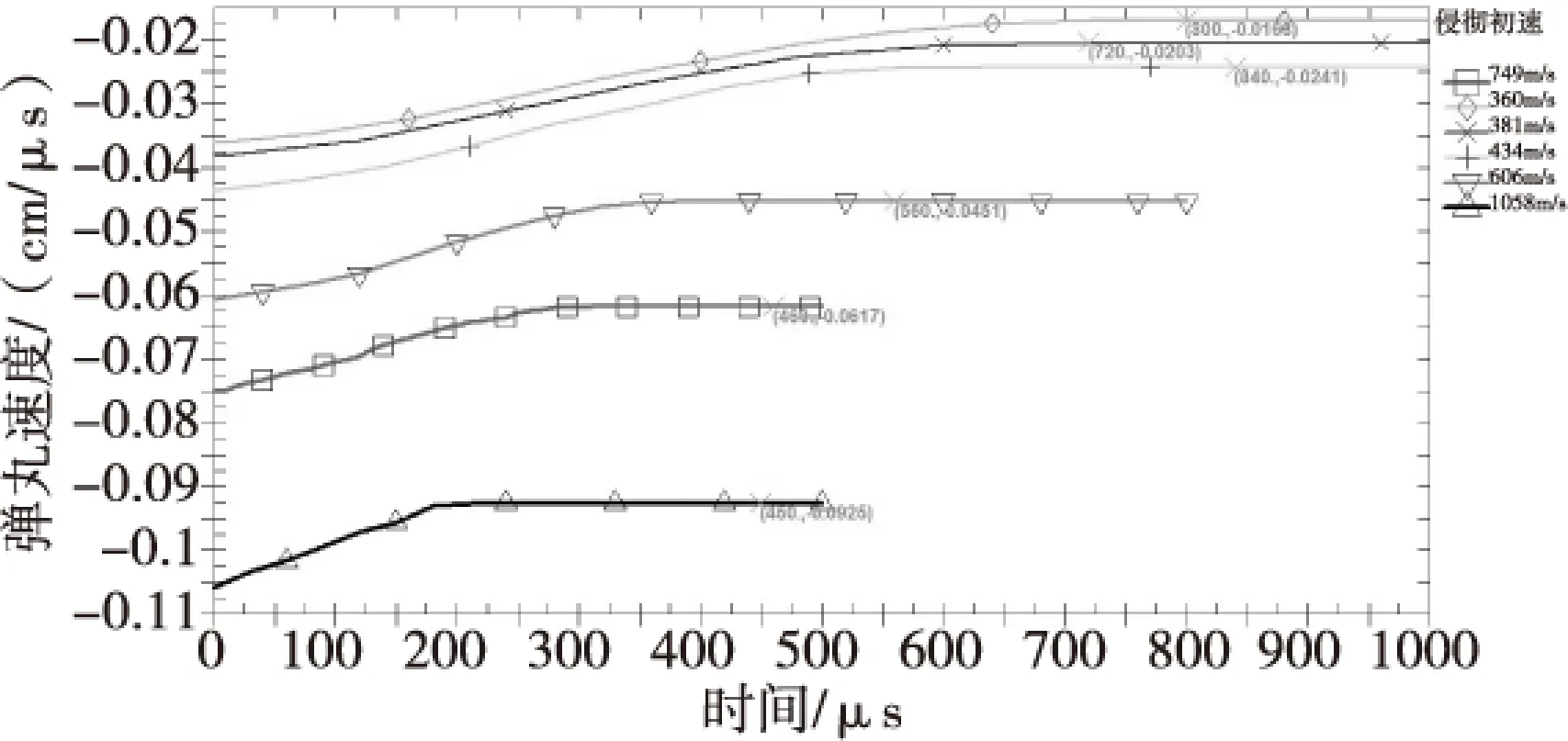
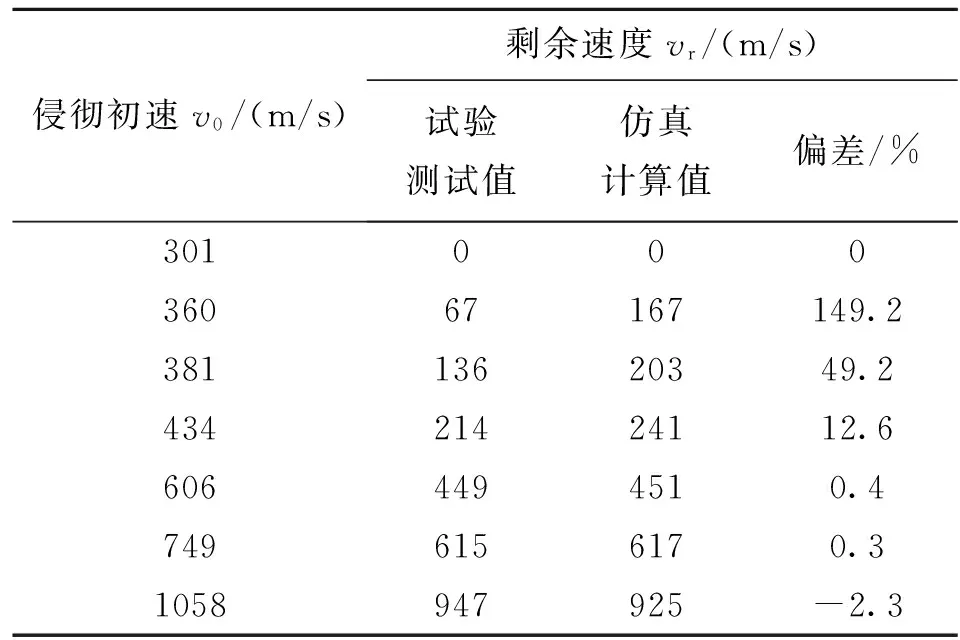
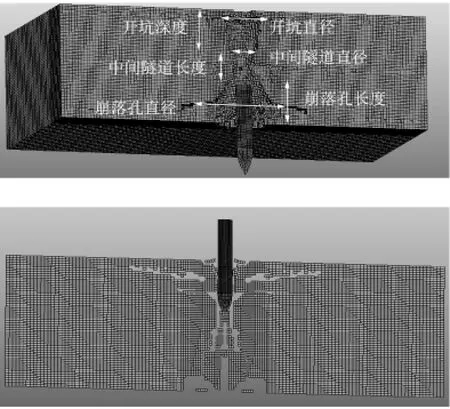
1)线弹性阶段(0 2)过渡阶段(Pcrush≤P≤Plock)时,这一阶段是指混凝土内部的气泡开始破裂,混凝土结构受到损伤,并开始产生破碎性裂纹,但混凝土结构还没有完全破碎。 P=Pcrush+Kcrush(μ-μcrush) (3) 式(3)中,Kcrush=(Plock-Pcrush)/(μlock-μcrush),Plock为材料空隙全部闭合时的临界压力,μlock为对应的体积应变。 3)压实阶段(P>Plock)时,当压力达到Plock,混凝土内部气孔被完全压碎。关系式常用三次多项式表示: (4) 1.2 屈服面方程 HJC模型的屈服面可表述为: (5) 1.3 损伤演化方程 HJC损伤模型如图2所示。模型损伤由塑性应变累积而成,其中塑性应变包括了等效塑性应变和塑性体积应变。其损伤演化方程为: (6) (7) (8) 式中,ΔεP和ΔμP分别为当前积分步下的等效塑形应变增量和塑性体积应变增量,P是实际的压力,EFMIN是材料最小破碎应变,T*=T/fc为无量纲最大静水压力。f(P)为常压P作用下材料发生断裂时的塑性应变。 图2 HJC材料损伤模型Fig.2 Damage model of HJC 2.1HJC自带失效准则与参数(FS)分析 HJC材料模型材料单元破坏的双门开关是等效塑性应变ε和损伤度D。而手册中HJC材料模型关键字文件里提到“FS>0时,当单元的有效塑性应变>FS失效”[12]。基于此可以很初步推得如下假设:FS是HJC材料模型在压力P作用下材料发生断裂与否的塑形应变的阈值。即可用下式表示为: FS=f(P)max=D1(Pmax*+T*)D2 (9) 结合式(7)和式(9)得到FS实际的意义如下:1)当设定FS>0时,表示选择了材料受压失效模式,FS的值是材料等效塑性应变失效控制的下限阈值;2)当设定FS=0时,由式(9)可知P*+T*=0即P*=-T*,即压力为无量纲最大静水压力的负值(实际为拉应力),表示材料选择了拉伸损伤失效模式,FS的值是无量纲静水拉力的阈值,当拉应力-P*>T*材料失效;3)当设定FS<0时,结合式(7)和式(9)可得D<0表示材料选择了损伤程度D控制失效模式,当材料累积损伤程度D<0时材料宣告失效。 由上述该材料的本构模型可以看出P随体应变μ的增大而增大,而混凝土材料模型在压实阶段存在一个压实密度ρcom,当混凝土介质受到高速高压冲击时其密度会迅速地由初始密度ρ0达到压实密度ρcom,进入压实密度以后材料继续受压其密度变化十分微小,从而可以合理假设:当材料受压的压力成倍地增长而相应的密度变化却小于1%时,可认为混凝土材料已经达到其极限密度ρmax,即:ρmax=(1+0.01)ρcom。相应此时的体应变达到最大值μmax,混凝土承受最大静水压Pmax。而从文献中可以查阅到压实密度的数据ρcom=2.68 g/cm3。 从而由上述假设可以得到材料的压缩极限密度ρmax,结合压实阶段状态方程(4)以求出μmax和Pmax。并将求出的Pmax带入式(9),从而可以量化计算出FS的数值为1.3。 2.2LSDYNA提供的多种单元失效准则 LSDYNA通过关键字*MAT_ADD_ERROSION提供了多种辅助单元失效准则。常用的失效准则有:最大静水拉(压)应力失效准则(拉为正,压为负)、最大主应力失效准则、最大等效应力失效准则、最大主应变失效准则、最大剪应变失效准则、等效塑性应变失效准则等。 2.3 侵彻钢筋混凝土目标的失效准则的选择 一方面由于侵彻钢筋混凝土目标涉及到靶板正面开坑、贯穿孔径、漏斗坑以及靶板背面的层裂与崩落现象。其中用最大单元剪应变失效准则控制可以有效地模拟出靶板的正面开坑现象;且单就HJC材料本构模型而言,该本构模型在模拟混凝土的压缩失效方面具有较为理想的效果(剩余速度和侵彻深度方面),故而采用HJC自带失效准则的压缩失效模式(控制参数FS=1.3)并联合剪应变失效准则共同控制单元压缩失效。 另一方面由于HJC本构模型在拉伸失效方面的描述不足,无法模拟出侵彻混凝土目标时的靶背崩落、层裂以及漏斗坑现象,故而还需要添加最大静水拉应力失效准则与最大拉伸主应力失效准则共同模拟钢筋混凝土材料受到侵彻时所受的拉伸失效。 参考S.J.Hanchak等试验的动能弹侵彻钢筋混凝土所用的弹靶尺寸。用分离式方法建立钢筋混凝土靶板的有限元模型,并采用上述方法所确定的单元失效准则与参数,对弹丸侵彻钢筋混凝土靶板的动态响应过程进行数值模拟。关注点侧重于数值模拟获取的侵彻过载信号与侵彻靶板的贯穿孔通道以及钢筋网络破坏情况和整体靶板的破坏工况。 3.1 剩余速度与减加速度分析 在数值模拟中同样采用靶场试验所用的相同的一系列弹丸入射速度来模拟,并将数值模拟结果所得的剩余速度与靶场试验所得的数据进行比对。以各种不同入射速度侵彻的数值模拟剩余速度结果如图3所示。 而关于侵彻过载的另外一个重要信号:弹丸减加速度信号,图4中清晰地表现了弹丸侵彻靶板时三层钢筋网对于弹丸速度的扰动影响,并且由此可以合理的推论出高配筋率的钢筋网对于防护侵彻能有极为正面的作用[13]。 图3 各种不同初速侵彻时弹体速度变化曲线Fig.3 Chart of projectile’s velocity in various initial velocities’ penetration projectile’s 图4 749 m/s初速侵彻的加速度过载曲线Fig.4 Chart of acceleration in duration of penetration by 749 m/s impact 最后进一步将数值模拟的剩余速度与前人若干侵彻试验所测得的剩余速度做更为直观的统计,如表1所示。 表1 剩余速度统计对比表 从表1可以看出,该数值模拟方法在侵彻初速大于600m/s以上时误差较小,获得的侵彻过载信号在速度和加速度方面都与试验数据接近,偏差不大。 侵彻过程中弹尖对周围的靶体材料产生挤压,当挤压过程产生的侧向应力大于靶体材料的抗剪强度(剪切失效应变控制)时,靶体材料就产生了剥落,应力越大,产生的剥落块就越大,即正面开坑。本文单就剪切失效应变阈值而言设置略微偏大,导致在靶体侧向损耗弹丸动能方面模拟略为不足,尤为明显地表现在当着靶速度低于600m/s时,侧向应力不足以让剪切失效发挥作用,开坑剥落比实际小许多,从而弹丸动能损耗偏小,影响的结果是剩余速度失真且数值偏大。因本文是验证不同着靶速度以相同的失效准则与参数控制下的侵彻结果,所以没有按照着靶速度等不同初始条件去调整失效准则的控制参数,且统一对照组里如果将剪切失效阈值调低,中高速侵彻剩余速度会失真,偏小。现实模拟时,可按照侵彻初始条件不同相应地去合理调整失效准则的控制参数以达到理想的模拟结果。 3.2 混凝土靶板贯穿破坏工况分析 图5和图6分别为弹体以749m/s初速侵彻钢筋混凝土时靶板的正面和背面损伤图。可以看出正面靶板的破坏损伤主要显现的是压缩破坏损伤,由靶板侵彻通道的开坑口向靶板边缘有相对较长的径向裂纹,且在开坑口附近有环形的小裂纹。从数值模拟与试验实际情形的对比图可以看出,靶板的正面开坑破坏情形除了开坑略浅,其他与试验结果比较吻合。而靶板背面破坏区域有较长较大的径向裂纹和环向裂纹,拉伸破坏现象较为明显。 图5 靶板正面损伤试验与数值模拟情况的对比Fig.5 Damage of target’s front face compare between experiment and simulation 图6 靶板背面损伤与数值模拟情况的对比Fig.6 Damage of target’s back face compare between experiment and simulation 自由面反射形成的拉伸波在靶板内形成裂纹并扩散从而导致了层裂现象出现,弹体在侵彻过程中在靶板的正面和背面都产生了一个圆锥体的漏斗形的弹坑。与Hanchak等人的试验进行比对,并从数值模拟的侵彻贯穿通道情况图7和图8可以看出,数值模拟的结果与试验结果情形吻合得较为良好。而靶板背面的崩落现象产生的原因是由于自由面附近应力的叠加合成产生拉伸损伤[14],如图8所示。 从图7和图8可以看出,本文采取的失效控制参数能有效地模拟出开坑、层裂、崩落、漏斗坑等侵彻混凝土目标时产生的各类靶板破坏形态。随着弹体速度的增大,侵彻开坑直径、中间隧道的直径、崩落孔的直径和崩落的长度也随之增大,而中间隧道的长度随之略微减小。其中单就749m/s初速侵彻工况来看,其数值模拟的工况为:侵彻开坑直径约为弹体直径的2倍(而试验约为2~2.5倍),崩落孔直径约为弹体的4.5倍大小(试验的大小约为5倍),中间隧道长度与靶板前后面的漏斗形坑长度近乎各占1/3,这也与文献[15]所述相符。 图7 360 m/s和434 m/s初速侵彻条件下数值模拟的侵彻贯穿通道情况Fig.7 Simulation of 360 m/s and 434 m/s impact target’s penetration path 图8 数值模拟749 m/s初速的侵彻贯穿通道与崩落的剖面示意Fig.8 Simulation of 749 m/s impact target’s penetration path and its collapse 3.3 钢筋网变形与破坏工况分析 图9 三层钢筋网的破坏与变形情况Fig.9 Destruction and deformation condition of 3 layers reinforced steel 弹丸侵彻钢筋混凝土靶板时,弹丸侵彻完靶板正面保护层水泥撞击到第一层钢筋网,弹丸撞击靶板使得靶板在径向受到冲击压力,进而使得钢筋网眼的变形在铺层面上沿径向变化。具体变形情况和破坏情况从上面两图可以看出:第一层钢筋网的挠度变形与侵彻冲击的方向相反;而第二层钢筋网的变形破坏仅有些微的层面外胀;第三层钢筋网的挠度变形则与侵彻冲击方向相同。同等直径大小的钢筋,弹丸的速度或者质量越大,钢筋变形越大,破坏越显著。类似的计算现象在文献[15]中也曾出现并被提及过。 本文提出了基于HJC材料模型的钢筋混凝土侵彻仿真失效准则与参数的方法,该方法是基于HJC材料模型自带的失效准则定义,运用LSDYNA算法修正HJC材料模型中的失效控制参数FS,采用上述模型自带的失效准则与参数并联合其他三种辅助失效准则来弥补HJC材料模型在失效定义方面的不足。实际侵彻试验结果表明,该数值模拟方法产生的侵彻贯穿现象与试验结果基本相同,因此该数值模拟方法具有一定的工程价值。 [1]聂明飞,李玉龙.卵形头部弹侵彻单多层混凝土靶板有限元仿真[J].探测与控制学报,2009,31(4):78-83. [2]周宁,任辉启,沈兆武,等.侵彻钢筋混凝土过程中弹丸过载特性的实验研究[J].实验力学,2006,21(5):572-578. [3]李猛深,李宏,冯淑芳.弹体侵彻钢筋混凝土的数值计算方法研究综述[C]//第四届全国工程安全与防护学术会议论文集.洛阳:中国岩石力学与工程学会,2014: 659-662. [4]TaylorLM,ChenEP,KuszmaulJS.Micro-crackinduceddamageaccumulationinbrittlerockunderdynamicloading[J].ComputerMethodsinAppliedMechanicsandEngineering,1986,55:301-320 [5]RiedelW,ThomaK,HiermaierS,etal.PenetrationofreinforcedconcretebyBETA2B2500numericalanalysisusinganewmacroscopicconcretemodelforhydrocodes[C]//9thInternationalSymposium,InteractionoftheEffectsofMunitionswithStructures.Berlin-Strausherg:I13MAC,1999:315-322. [6]HolmquistTJ,JohnsonGR.Acomputationalconstitutivemodelforconcretesubjectedtolargestrains,highstrainratesandhighpressures[C]// 14thInternationalSymposiumonBallistics,Canada,1993:591-600. [7]JavierLMalvar,CrawfordJohnE,WesevichJamesW,etal.AplasticityconcretematerialmodelforDYNA3D[J].InternationalJournalofImpactEngineering,1997,19(9):847-873. [8]马爱娥,黄风雷,李金柱,等.钢筋混凝土抗贯穿数值模拟[J].北京理工大学学报,2007,27(2):103-107. [9]王建刚.子弹侵彻钢筋混凝土的数值模拟研宄[D].北京:国防科学技术大学,2011. [10] 胡怀春.侵彻混凝土目标贯穿特性分析及靶后炸点精度控制研究[D].南京:南京理工大学,2014. [11]林华令,丁育青,文辉.混凝土侵彻数值模拟的影响因素[J].爆炸与冲击,2013,33(4):425-429. [12]姜华,王君杰.弹体侵彻混凝土数值模拟失效指标[J].振动与冲击,2009,28(8):30-34. [13]LS-DYNAkeywordsusre'smanual(version971/Rev5)[M].California:LivermoreSofewareTechnologyCorporation,2010. [13]楼建锋,王政,朱建士,等.含筋率和弹着点对钢筋混凝土抗侵彻性能的影响[J].爆炸与冲击, 2010, 30(2): 178-182. [14]武海军, 黄凤雷 ,金乾坤,等.弹体贯穿钢筋混凝土数值模拟[J].爆炸与冲击, 2003, 23(6): 545-550. [15]庞洪鑫.高速侵彻钢筋混凝土靶板的数值模拟研究[D].北京:北京理工大学,2015. The Failure Criterions and Parameters of HJC Model Based Perforation Simulation LIN Chen1,XU Jianjun1, YANG Jinwei2,ZHANG Hailiang2 ( 1. College of Mechanic and Electronic Engineering,North University of China,Taiyuan 030051,China; 2. HuaiHai Industrial Group.,Ltd, Changzhi 046000,China ) Aiming at the inadequate descriptions in definitions of elements’ failure for the various constitutive models of reinforced concrete, a new approach by rectifying the parameter FS of HJC material model ,base on LSDYNA’s algorithms was presented. By adopting the combinations of criterions of element’s failure, which was offered by FS and LSDYNA, the numerical simulation of projectile’s penetration into reinforced concrete was carried out. It was proved that this method had a certain value in engineering by contrasting with the counterpart practical experiments. HJC; perforation; reinforced concrete; numerical simulation; failure criterions 2016-10-22 林琛(1989—),男,江西上饶人,硕士研究生,研究方向:机电控制系统。E-mail:814035759@qq.com。 TJ430.6;TM89 A 1008-1194(2017)02-0100-06
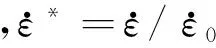
2 单元失效准则与参数
3 数值模拟与试验的对比验证





4 结论
