离心力驱动引信水平转子质心优化方法
2017-05-25王雨时张志彪
刘 宣,闻 泉,王雨时,张志彪
(南京理工大学机械工程学院,江苏 南京 210094)
离心力驱动引信水平转子质心优化方法
刘 宣,闻 泉,王雨时,张志彪
(南京理工大学机械工程学院,江苏 南京 210094)
针对引信离心力驱动水平转子转动可靠性难以保证的问题,提出了离心力驱动引信水平转子质心优化方法。该方法是通过建立引信水平转子转正过程动力学方程,得到其质心回转半径与初始方位角的最优解关系式。仿真验证表明,初始方位角取值不同对引信水平转子动态运动特性影响较大,优化得到的最优质心回转半径及质心初始方位角能使得水平转子转动过程中的净驱动力矩值始终较大,从而有助于提高旋转弹引信水平转子转正正确性。
引信;转子隔爆机构;解除保险可靠性;优化设计;动力学仿真
0 引言
离心力矩驱动的引信水平转子均为有轴转子,其质心偏离转轴且回转平面垂直于弹轴,广泛用于旋转弹引信特别是中大口径旋转弹引信隔爆机构,具有占用轴向尺寸小、充分利用径向空间、隔爆距离容易满足、无内贮能用作解除保险动力的特点。文献[1-3]分析了离心力驱动水平转子受力,建立水平转子动力学模型且对转子转正到位所需的时间作了概略分析。文献[4]针对隔爆部件在钟表机构轮系失效时可能引起的炮口炸问题,提出一种通过调整回转体部件质心来消除此种危险的结构设计思想。文献[5-7]运用Adams软件对水平转子驱动的无返回力矩钟表机构进行仿真分析,介绍了仿真分析方法,探究了机构动态运动特性。
但上述文献均未涉及离心力驱动引信水平转子质心优化设计问题。由于水平转子的主动力和摩擦力及其力矩主要与弹丸转速有关,所以水平转子在弹道上能否可靠转正主要取决于其质心相对于转轴和弹轴的位置。当转子转轴与弹轴的位置关系确定后,转子质心与转轴的距离及其方位角是影响转子转正可靠性的关键因素。无延滞效应的纯水平转子转动起来之后,靠惯性作用,转子仍有可能越过略微靠近的某些不利的方位。而有无返回力矩钟表等机构延滞效应的水平转子,其转动速度较慢,惯性作用影响很弱,在接近某些不利的方位时,就有可能会停止转动。本文针对离心力驱动水平转子转正可靠性难以保证的问题,提出了离心力驱动引信水平转子质心优化方法。
1 引信水平转子基本结构
美国中大口径榴弹弹头起爆引信M739A1采用离心力驱动的水平转子作为隔爆件,如图1所示。

图1 M739A1弹头起爆引信Fig.1 M739A1-nose detonate fuze
水平转子式隔爆机构解除保险(即解除隔离)转角γ较大。其中,榴-5引信为153°,前苏联4MP引信为175°,海甲-1引信为125°,美M20A2传爆装置为105°[1-2]。离心力驱动的水平转子式隔爆机构典型结构[2]如图2所示。

图2 离心力驱动的水平转子隔爆机构Fig.2 Horizontal rotor of explosion-proof structure drived by centrifugal force
回转体上的雷管与导爆药错开一个角度以保证引信平时的安全性。发射后,旋转弹丸围绕其弹轴暨引信轴线旋转,水平转子在离心力的驱动下绕其转轴并朝着雷管与导爆药可对正的方向转动,加重子用于调节水平转子的质心位置,确保转正可靠。当转子转正到位时,雷管与导爆药柱对正,水平转子解除保险。
2 引信水平转子质心位置优化方法
2.1 旋转弹引信水平转子转正过程受力分析
引信水平转子在转正到位的过程中,其质偏既产生驱动力矩,也产生摩擦力矩。为保证离心力驱动的引信水平转子转正的可靠性,驱动力矩必须始终大于诸摩擦力矩之和,即应有净驱动力矩M大于0。

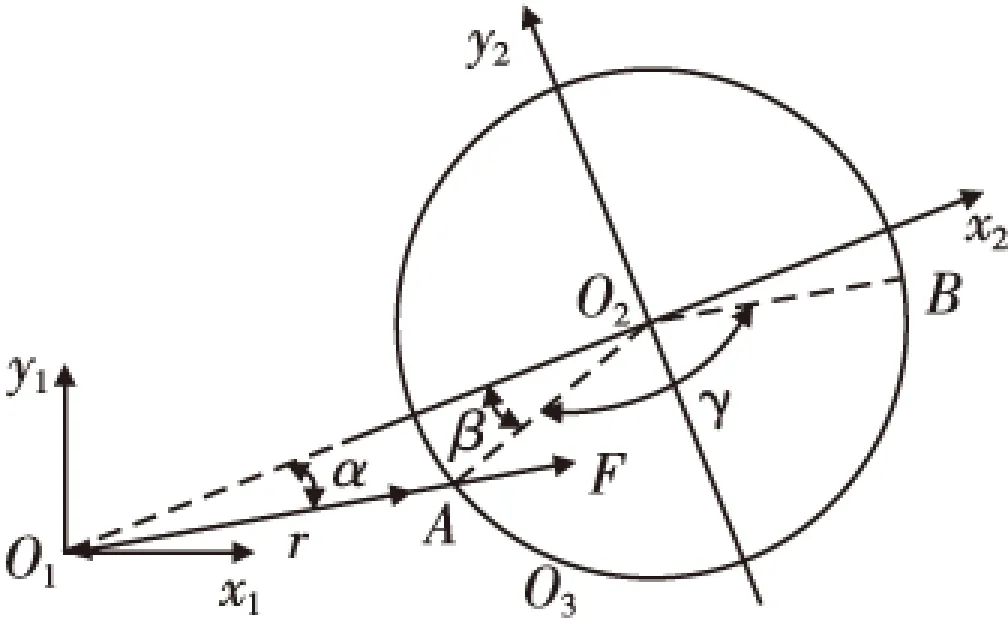
图3 水平转子简化模型Fig.3 Simplified model of horizontal rotor
本文研究的是离心力驱动引信水平转子,通常都配有延期解除保险机构,水平转子在弹丸出炮口后才开始运动。在此阶段,水平转子还受章动力、爬行力和切线惯性力的作用。章动力系周期性力,章动力和爬行力对于水平转子的转正运动只是通过轴向约束反力产生的摩擦力矩起作用,并不影响水平转子质偏位置的优选问题。相对于质偏产生的转正力矩而言,章动力和爬行力所产生的摩擦力矩较小,因而可以忽略不计。在外弹道阶段,切线惯性力很小,也可以忽略不计。当然上述简化会使整个分析结果偏于冒进,设计时适当留出解除保险主动力矩裕量即可。
水平转子在转动过程中,主要受离心力产生的主动力矩Mo,离心力产生的转子轴上的摩擦力矩Mof,后坐惯性力产生的转子下平面上的摩擦力矩Msf的作用,其净驱动力矩为:
M=Mo-Mof-Msf
由图3所示的水平转子简化模型及其受力特性可知:
(1)
式(1)中,m为水平转子质量,ω为弹丸旋转角速度,f为转子与转子轴或转子与转子座或转子轴与转子座之间的摩擦系数,d为转子轴直径,V为弹丸运动速度,R1为水平转子与转子座摩擦接触圆环面小圆半径,R2为水平转子与转子座摩擦接触圆环面大圆半径,由于转子的质心位置由质心旋转半径l及方位角β决定,故将上式进一步简化得:
(2)
针对R1=0的普遍情形,式(2)可进一步化简为:
(3)
由式(3)以及解除隔离转角γ值可知,一般情况下水平转子初始方位角β0<90°。欲使水平转子从初始方位角β0开始转动,净驱动力矩M应大于0。按式(3)给出的表达式,M会随β的增大而呈先增大后减小的变化趋势。
令βM为转子整个运动周期内净驱动力矩M取得最大值时的方位角,βT=β0+γ为机构终止位置方位角。βM可通过迭代算法由下式得出:
(4)
净驱动力矩M在[β0,βM]单调递增,在[βM,βT]单调递减,且净驱动力矩最小值将在初始方位角β0或终止位置方位角βT处取得。
水平转子β0的不同取值会使机构有不同的驱动状态,对应的净输出力矩值变化过程也会存在差异。如果水平转子满足条件:
1)弹轴O1、转子轴O2和质心轴O3三者不共线,且夹角β0≤180°-γ;
2)质心装配位置A点的净驱动力矩MA>0;
3)质心最终位置B点的净驱动力矩MB接近于质心装配位置A点的净驱动力矩MA,即MB≈MA,

由式(5)和式(6)可得离心力驱动的水平转子能够满足转动条件的质心旋转半径l及初始方位角β0的范围,式(7)给出了质心旋转半径l与初始方位角β0之间的关系。
2.2 算例分析
为形象地描述水平转子质心位置对引信水平转子转正正确性的影响,以某旋转弹引信水平转子为仿真研究对象,利用Matlab软件对机构运动特性进行数值分析。表1给出了引信旋转环境参数和水平转子初步设计参数。

表1 引信旋转环境参数和水平转子初步设计参数

表2 初始方位角β0计算数值
取质心旋转半径l=5 mm、初始方位角β0=13°,得到水平转子主动力矩、摩擦力矩、净驱动力矩随转角β的变化曲线如图4所示。将上述数据代入式(4),经迭代计算,可得βM=88.204°。

图4 l=5 mm、β0=13°力矩随转角β变化曲线Fig.4 l=5 mm、β0=13°curve of torque-angle of rotation
由图4可知,在水平转子整个转动周期内,摩擦力矩一直在增加,主动力矩和净驱动力矩均是先增大后减小;当质心旋转半径l=5 mm时,在满足可靠转动条件(0.92°≤β0≤30°)下,取离心力驱动的引信水平转子初始质心位置方位角β0=13°,初始质心位置净驱动力矩接近于最终位置值,则整个运动周期净驱动力矩值的最小值将达到最大。
3 仿真验证
为进一步研究引信水平转子质心旋转半径l及初始方位角β0(装配位置)对机构在整个运动周期内的影响,验证理论分析的正确性,针对上述某旋转弹引信水平转子,运用ADAMS软件进行仿真。模型如图5所示,该模型主要由水平转子部件组成,且由上、下盖板支撑限位。

图5 仿真模型Fig.5 Simulation model
将三维模型导入ADAMS软件中,并赋予零部件质量属性,将仿真模型中转子、转子轴、齿弧、雷管、加重子通过布尔运算组成转子部件,定义上夹板与下夹板间的固定约束副,定义下夹板的旋转副,使其绕旋转中心以ω=245 r/s匀速转动,定义转子部件与上夹板、下夹板之间的接触,并定义接触之间的摩擦系数f=0.20。
调节水平转子初始质心位置,使其满足转子质心旋转半径l=5 mm、初始方位角β0取5°,7°,9°,11°,13°,15°,17°,19°,21°,23°,研究引信水平转子初始质心方位角β0对机构整个运动周期净驱动力矩M的影响。由理论分析和仿真计算得到水平转子在整个运动周期内净驱动力矩M最小值,如表3所列。

表3 β0取不同值对应净驱动力矩M最小值
由表3可得,β0取不同值得到的净驱动力矩Mmin仿真结果与理论结果相近,误差不超过 17%,其误差可能是由于仿真过程中水平转子的上下攒动以及转动过程中接触产生的摩擦被过渡简化。水平转子初始质心位置β0不同,得到的净驱动力矩Mmin也不同,且β0≈13°时,净驱动力矩Mmin取得最大值(理论值18.24×10-3,仿真值21.11×10-3)。对离心力驱动的引信水平转子质心位置进行优化分析,得到初始方位角β0的最优解,使得机构运动过程中净驱动力矩Mmin值增大,有助于提高转子转正的可靠性。
离心力驱动的水平转子往往要与具有计时功能的机构如钟表机构共同作用以满足引信延期解除保险性能。因此,对一系列的l、β0最优解具体选择还要结合结构设计可能性和其他机构的动态特性。一种小口径榴弹发射器引信离心力驱动的水平转子以及具有延滞效应的无返回力矩钟表机构,实物如图6所示,水平转子如图7所示。
通过对比两次靶场射击试验结果可知:引信水平转子质心旋转半径l与初始方位角β0的选择对水平转子转正可靠性有较大影响。第一次靶场射击试验中水平转子存在未能转正到位的现象,调整质心旋转半径l与初始方位角β0使其尽可能满足上述理论分析条件之后,第二次靶场射击试验水平转子能保证可靠转正。

图6 一种小口径榴弹发射器引信安全和解除保险装置Fig.6 Safe and arming device of a small-caliber grenade launchers

图7 水平转子模型图Fig.7 Model diagram of horizontal rotor
4 结论
本文提出了离心力驱动引信水平转子质心优化方法。该方法是通过建立引信水平转子转正过程动力学方程,得到其质心回转半径与初始方位角的最优解关系式。仿真验证表明,初始方位角β0的不同取值对引信水平转子动态运动特性影响较大,优化得到最优质心旋转半径l及质心初始方位角β0使得机构运动过程中净驱动力矩Mmin值增大,有助于提高旋转弹引信水平转子转正可靠性。
[1] 孔华,王雨时,嵇振涛,等.引信离心力驱动垂直转子起动特性[J].探测与控制学报,2015,37(3):53-56.
[2] 孔华,王雨时,嵇振涛,等.引信离心力驱动垂直转学动力学模型[J].探测与控制学报,2015,37(1):36-40.
[3]宋荣昌,申跃跃,许恩德,等.引信安全系统动态特性及膛内安全性研究[J].北京理工大学学报,2015,35 (8):796-799.
[4] 王立新.引信无返回力矩钟表机构虚拟样机技术研究[D].南京: 南京理工大学,2004.
[5] 裴晓辉.无返回力矩擒纵机构振动周期研究及仿真分析 [D].沈阳: 沈阳理工大学,2008.
[6] 刘刚,陆静,姚智勇,等.基于虚拟样机的无返回力矩钟表机构仿真分析[J].计算机仿真,2013,30(2):388-391.
Centrifugal Fuze Horizontal Rotor Centroid Position Optimization
LIU Xuan,WEN Quan,WANG Yushi,ZHANG Zhibiao
( Mechanical Engineering school, NUST, Nanjing 210094, China)
For the problem that the centrifugal fuze horizontal rotor failled to rotate correcttly, an optimal design on centroid position of horizontal rotor was put forward. This method set up kinetic equations of rotating of horizontal rotor to get the optimal relational expression of radius of gyration and initial azimuth.Simulation results showed that the value of initial azimuth had a greater impact on dynamic motion characteristics of horizontal rotor. And the optimal radius of gyration and initial azimuth could make the value of net driving torque comparatively larger during the rotation of horizontal rotor. which improved the rotating correctness of fuze horizontal rotor.
fuze;rotor interrupter device;arming reliability;design optimization;dynamics simulation
2016-10-20
刘宣(1989—),男,山东济宁人,硕士研究生,研究方向:引信系统分析和机构动力学。E-mail:15564864028@163.com。
TJ431.3
A
1008-1194(2017)02-0024-05
