大型风电机组的比例-积分-谐振独立变桨距控制策略

杨文韬 ，耿 华 ，肖 帅 ，杨 耕

（1.清华大学 自动化系，北京 100084；2.北京控制工程研究所，北京 100190）

0 引言

随着现代大型风电机组单机容量的不断增大，风电机组机械零部件的尺寸和重量也在不断增加，使得风电机组的制造成本升高［1］。风轮直径和扫掠面积的增大，会导致机组承受的载荷更大、更复杂，从而降低了风电机组的使用寿命［2-3］。通过变桨距调节进行主动载荷控制，可以降低机组所承受的载荷，提高系统的可靠性以及延长机组的使用寿命，从而有效地提高风电机组的经济效益［4］。

风电机组运行的过程中，湍流、风的剪切效应、塔影效应以及偏航误差等因素会造成风轮各面受力不均，从而使得风轮承受不平衡载荷。随着风轮半径的增大，这种不平衡载荷的存在变得愈发明显。风轮所承受的不平衡载荷会对变桨轴承、轮毂、主轴、偏航轴承及塔架等部件造成很大的疲劳载荷［5］。传统的统一变桨距控制方式，各桨叶变桨机构是同步变化的，因此无法抑制不平衡载荷。独立变桨距控制可以对各桨叶变桨机构独立进行调节，因此可以有效降低风轮的不平衡载荷［6-7］。现代大型风电机组大多都安装了独立变桨距执行机构以及载荷传感器，为独立变桨距控制的实现提供了所需条件。

对于独立变桨距控制策略的研究，基本都是针对工作在第3工作区的风机，目前国内外已经有一些研究成果。文献［8］提出了一种独立变桨距控制策略，根据每个桨叶处的风速测量信息，通过调节每个桨叶的桨距角，使得各桨叶的攻角相同，从而降低风轮所承受的不平衡载荷。但是该方法在实际中实现较困难，且其本质是一种前馈控制，当测量不准确时，反而会增大桨叶所承受的不平衡载荷。文献［9］基于风机的线性周期时变模型，根据时变控制理论设计了独立变桨距控制器，但是这种时变控制器的设计比较复杂。现在采用较多的方法是基于MBC（Multi-Blade Coordinate）坐标变换［10］，将风机的线性周期时变模型变换为线性时不变模型，然后采用线性时不变控制理论的知识进行控制器设计。文献［5，11-12］建立了基于MBC变换后风电机组气动载荷计算的线性化模型，忽略控制环路之间的耦合，将控制器设计简化为SISO（Single-Input Single-Output）问题，然后采用PI控制器对不平衡载荷进行控制。该方法简单有效，且易于实现，但PI控制器只能抑制旋转部分不平衡载荷的低频分量（1p，p为风轮旋转频率的倍数），无法抑制高频分量（2p、4p等）。在此基础之上，文献［13］对基本的MBC变换进行扩展，提出了可以抑制旋转部分不平衡载荷高频分量的独立变桨距控制策略，但是该控制算法需要进行多次MBC坐标变换，设计整定多个PI控制器，实现较为复杂。文献［14］提出一种基于串联校正的高次载荷控制策略，该算法中控制参数的整定需要采用数值优化方法，设计也较为复杂。

本文提出一种基于MBC坐标变换的比例-积分-谐振（PI-R）独立变桨距控制策略，其中PI部分用于抑制旋转部分不平衡载荷的低频分量（1p），R部分用于抑制高频分量（2p、4p）。该控制算法可以有效抑制不平衡载荷的低频以及高频分量，且控制简单，物理意义直观，易于工程实现。

1 气动载荷简化计算模型

桨叶所受气动载荷的模型为复杂的非线性模型。为了简化分析，将桨叶视为刚性叶片，并对气动载荷非线性模型在稳态工作点附近进行线性化。

1.1 气动载荷计算线性化模型

根据叶素动量（BEM）理论，忽略尾流效应以及不稳定空气动力学特性，可以得到风电机组的气动载荷线性化模型［13］，其中桨叶根部挥舞方向的弯矩变化量可以表示为：

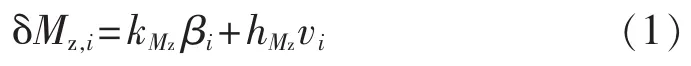
其中，δMz，i为第i个桨叶根部的挥舞方向的弯矩变化量；βi为第i个桨叶的桨距角；vi为第i个桨叶处挥舞方向有效风速；kMz、hMz分别为弯矩在工作点处对桨距角和相对风速的偏导数，可以表示为式（2）。

叶片处挥舞方向有效风速是由绝对风速u和塔架轴向振动引起的相对风速合成的，可以表示为［13］：

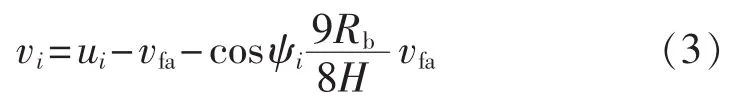
其中，vfa为塔架顶部轴向速度；ui为第i个桨叶的绝对风速；ψi为第i个桨叶的空间位置角，桨叶竖直向上时为0°；Rb为桨叶半径；H为塔架高度。式中等号右侧第二项表示了塔架轴向位移对有效风速的影响，第三项表示了塔架俯仰转动的影响。风轮所承受的不平衡载荷主要包括俯仰弯矩Mtilt和偏航弯矩 Myaw，可以表示为［13］：

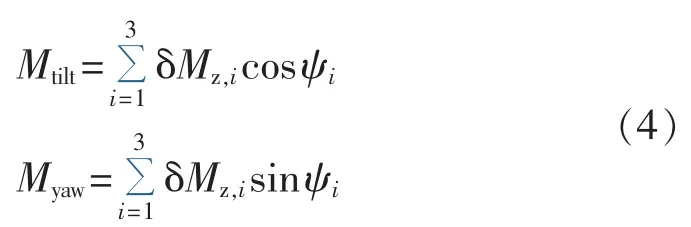
将式（1）和式（3）代入式（4），可得：

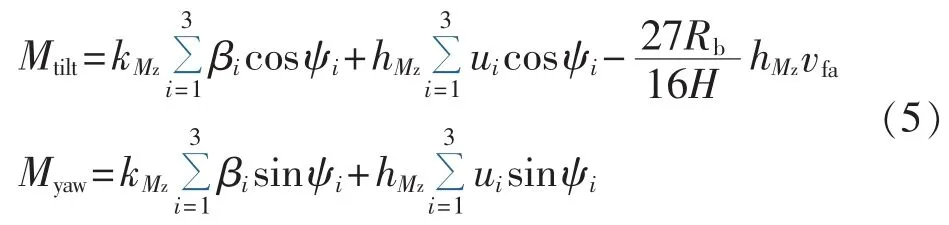
1.2 MBC坐标变换

式（5）给出了基于线性化模型得到的俯仰弯矩和偏航弯矩的载荷计算表达式，但是由于式中存在周期性时变的系数，无法采用传统的线性定常控制理论进行控制器设计。MBC坐标变换可以将风电机组在混合坐标系下表示的线性周期时变模型变换为在静止坐标系下表示的线性时不变模型。基于MBC变换后的风电机组线性时不变模型，可直接采用发展成熟的线性时不变控制理论进行独立变桨距控制设计［10］。

MBC坐标变换也称Coleman坐标变换，最早应用于直升机控制领域。对于含有稳速旋转部件的系统而言，该变换能够很好地描述系统旋转部件和固定部件之间的关系，并甄选出特定频率的旋转分量。基于MBC变换将风电机组线性模型中在桨叶旋转坐标系下表示的物理量变换到在轮毂静止坐标系下表示的物理量，则变换后模型的所有物理量均是在静止坐标系下的，且模型的周期性变得很弱。对在不同桨叶转角下进行MBC变换得到的风电机组模型进行平均，就可以得到风电机组的线性时不变模型。在进行独立变桨距控制器设计时，只关心桨叶挥舞振动的不平衡分量，因此提取MBC变换后风电机组模型的不平衡分量，则可以得到用于独立变桨距控制器设计的风电机组线性化模型。对于三桨叶水平轴风机，其基本形式可以表示为：

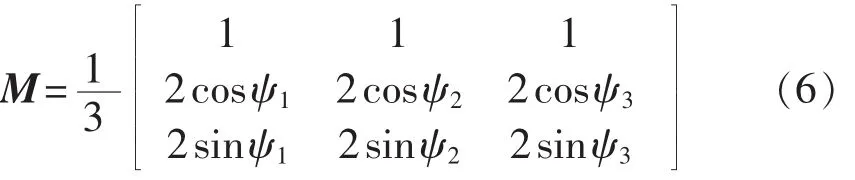
其逆变换可以表示为：

各桨叶的挥舞弯矩Mz，i、有效风速vi以及桨距角βi经过MBC变换后，表示为：

其中，下标0表示统一分量，下标c表示余弦分量，下标s表示正弦分量；M0表示平均弯矩，为平衡载荷；Mc、Ms分别表示俯仰方向和偏航方向弯矩，为不平衡载荷。Mc、Ms与俯仰弯矩和偏航弯矩之间的关系可以表示为：

将式（8）代入式（5），可以得到经过MBC坐标变换后的俯仰弯矩和偏航弯矩的表达式为：

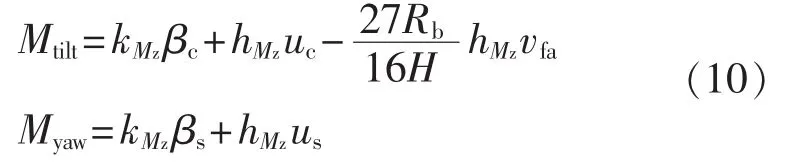
可见，经过MBC坐标变换后俯仰弯矩和偏航弯矩的载荷计算表达式为线性定常的，且两者之间是相互独立的，因此可以看作2个独立的SISO系统进行控制器设计。

2 PI-R独立变桨距控制策略

2.1 不平衡载荷频率分析

风电机组运行的过程中，由于对风电场的旋转采样、塔影效应、风的剪切效应以及偏航误差等，会导致桨叶处的有效风速vi含有风轮旋转频率的整数倍（np，n为整数）次频率分量。由式（1）可知，桨叶根部挥舞弯矩也将同样含有np次频率分量［15］。但是桨叶旋转坐标系下的挥舞弯矩频率分量，在轮毂固定坐标系下会发生变化，使得俯仰弯矩和偏航弯矩只含有3np次频率分量。下面对轮毂固定坐标系下载荷的频率进行分析。

假设桨叶根部挥舞弯矩含有mp（m为整数）次频率分量，此时桨叶根部挥舞弯矩的mp次频率分量可以表示为：

其中，Am为载荷mp次频率分量的幅值；ψ为桨叶1的空间位置角。根据m的取值不同，可以分为3种情况进行讨论，即 m=3k-1，3k，3k+1。

当 m=3k-1（k 为自然数）时，将式（11）和式（8）代入式（9），可以得到轮毂固定坐标系下的俯仰弯矩和偏航弯矩的表达式为：

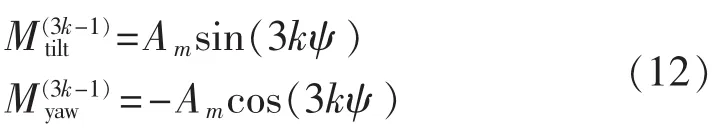
当m=3k时，有：

当m=3k+1时，有：

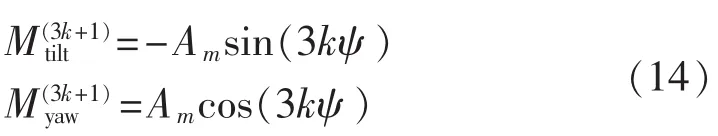
由上述表达式可知，桨叶旋转坐标系下Mz的（3k-1）p和（3k+1）p次频率分量在轮毂静止坐标系下会变成Mtilt和Myaw的3kp次频率分量，而桨叶旋转坐标系下Mz的3kp次频率分量在轮毂旋转坐标系下会相互抵消，不产生Mtilt和Myaw。具体地，旋转坐标系下Mz的1p次频率分量会变成Mtilt和Myaw的0 p次频率分量，旋转坐标系下Mz的2p和4p次频率分量会变成Mtilt和Myaw的3p次频率分量，旋转坐标系下Mz的5p和7p次频率分量会变成Mtilt和Myaw的6p次频率分量，依此类推。考虑到变桨距执行结构变桨速率有限，当Mtilt和Myaw的频率太高时，无法通过独立变桨距进行控制，反而会增加变桨距执行机构的疲劳，因此，一般只考虑抑制Mtilt和Myaw的0p和3p次频率分量。

2.2 PI-R独立变桨控制设计

由式（10）可知，独立变桨距控制器设计可以简化地看作是2个独立的SISO控制问题。采用传统的PI独立变桨控制算法可以有效抑制不平衡载荷的低频分量，但是对于高频分量（3p等）则无能为力，甚至会增大3p次频率分量。因此往往需要设计低通滤波器，将3p次频率分量滤除［14］。本文提出了一种PI-R独立变桨距控制算法，其中PI控制器用于抑制不平衡载荷的低频分量，而R控制器用于抑制不平衡载荷的3p次频率分量，从而进一步降低风轮所承受的不平衡载荷。

本文采用的控制系统的控制框图如图1所示。控制系统分为两部分：转速/功率控制器通过统一变桨距以及发电机电磁转矩控制，对风轮转速Ω和电磁转矩Te进行调节；独立变桨距控制器则通过调节各桨叶桨距角，降低风轮所承受的不平衡载荷。2个控制器输出的桨距角指令信号相叠加作为整个控制系统的桨距角控制指令值。

图1 独立变桨系统控制框图Fig.1 Block diagram of individual pitch control system

由图1可见，独立变桨距控制器基于各桨叶根部挥舞弯矩测量值，经过MBC变换后得到俯仰弯矩和偏航弯矩，然后以0作为给定值，采用PI-R控制器分别对俯仰弯矩和偏航弯矩进行控制，PI-R控制器输出的指令值再经过MBC反变换后得到独立变桨距控制器输出的各桨叶角指令值。其中PI-R控制器由两部分并联组成：一部分经过低通滤波器后，由PI控制器对低频分量进行控制；另一部分由R控制器对3p次频率分量进行控制。对于风电机组而言，桨叶主要疲劳载荷的频率分量均为低频分量。对于高频分量的抑制，不但不会有效降低桨叶疲劳载荷，还会大幅提升变桨距执行机构的动作速率，对执行机构自身造成不必要的疲劳载荷，因此需要在PI控制器前端串联低通滤波器。R控制器本身对输入信号特定频率的分量有很大的控制增益，对于输入的其他频率分量的增益则非常小（参见图2），所以在其前端不需要串联滤波器。R控制器的传递函数可以表示为：

图2 谐振控制器的幅频特性Fig.2 Amplitude-frequency characteristic of resonator controller

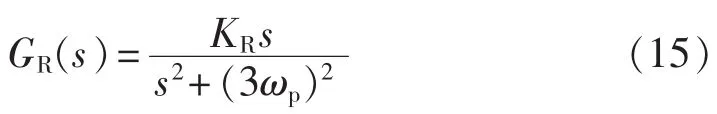
其中，KR为R控制器增益；ωp为风轮旋转频率。该控制器在频率为3ωp处的增益为无穷大，其幅频特性如图2所示。图2中频率的单位为rad/s，幅值的单位为dB。对3p分量而言，R控制器相当于是一个积分器，可对其进行幅值积分，进而实现无静差控制，有效抑制3p分量。

在实际系统中，在特定频率增益过大可能会带来系统稳定性问题，同时轮毂载荷在3p次频率附近的部分也不能忽略，因此采用非理想R控制器：

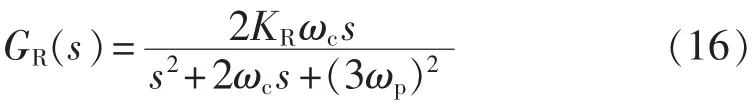
其中，比例增益KR与峰值处增益呈正比；旋转频率ωp与风机额定转速相关；剪切频率ωc对应带宽可近似为ωc/π，剪切频率越大，谐振峰越宽，谐振频率处增益越小。在本文的仿真实验中，取非理想R控制器参数为：KR=-2×10-5，3ωp=3.8 Hz，在设计带宽为0.4 Hz时，可得 ωc=1.26 Hz。

3 仿真结果

本文采用美国国家能源实验室NREL（National Renewable Energy Laboratory）开发的FAST软件对所提出的控制算法进行仿真验证。所采用的风机模型是1.5 MW的三桨叶水平轴风机，其主要参数如下：额定转子转速为20 r/min，额定功率为1.5 MW，切入风速为3 m/s，额定风速为12 m/s，切出风速为25 m/s，桨叶半径为35 m，塔架高度为82.39 m，转子转动惯量为2 962.44×103kg·m2，发电机转动惯量为53.036 kg·m2，齿轮箱变比为87.965。变桨距执行机构建模为一阶惯性环节，时间常数为0.25 s，桨距角最大变化速率为15°/s。风速模型由NREL开发的TurbSim软件生成，仿真中采用IEC61400-1标准，Kaimal功率谱模型，平均风速为14 m/s，风剪切系数为0.2。

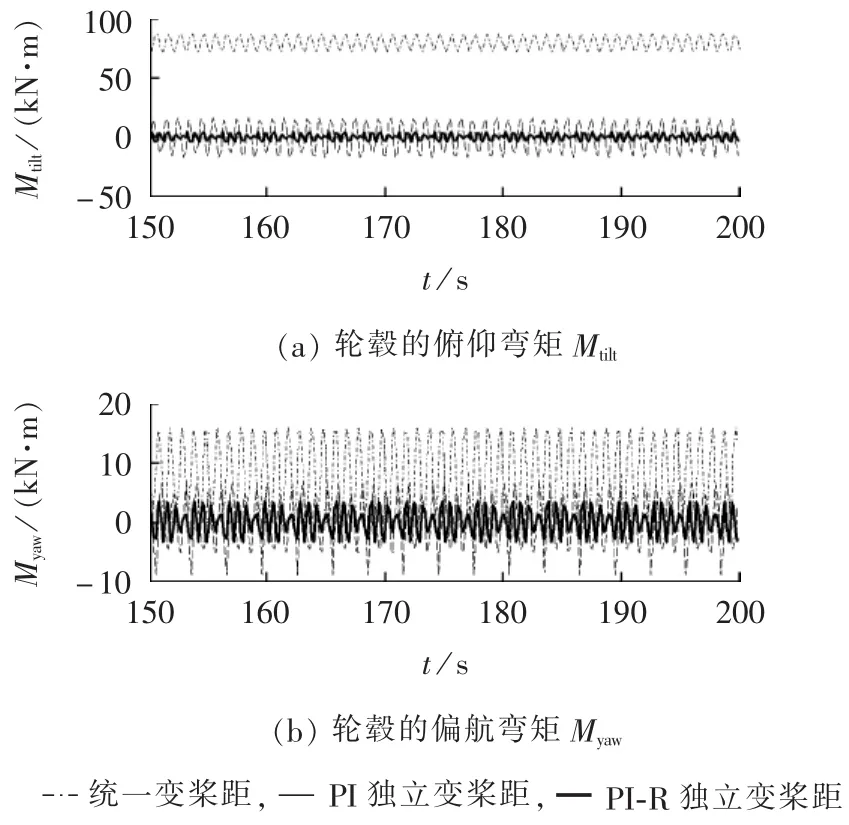
图3 稳态风速下不同控制算法的仿真结果Fig.3 Simulative results of different control algorithms under steady wind speed

图4 稳态风速下轮毂俯仰弯矩和偏航弯矩的FFT分析Fig.4 FFT analysis of tilt and yaw moments for hub under steady wind speed

稳态风速下不同控制算法的时域仿真波形如图3所示，其对应的频域分析如图4所示。其中风轮的额定转速为 20 r/min，则风轮旋转频率为 1/3 Hz。由仿真结果可见，在稳态风速下，只采用统一变桨距对转速或功率进行控制时，轮毂俯仰弯矩和偏航弯矩主要含有较大的0p和3p分量，其他频率分量非常小。由于风速在垂直方向上剪切效应明显，因此轮毂承受的俯仰弯矩要大于偏航弯矩。采用传统的PI独立变桨距控制可以有效降低0p分量，但是对3p分量没有作用。而采用本文提出的PI-R独立变桨距控制，可以同时抑制0p和3p分量。

10%湍流风速下不同控制算法的时域仿真波形如图5所示，其对应的频域分析如图6所示，加入了采用线性二次高斯LQG（Linear Quadratic Gaussian）独立变桨控制［6］的仿真结果。在湍流风速作用下，轮毂俯仰弯矩和偏航弯矩除含有较大的0p和3p分量外，还含有较多的其他随机频率的分量。与稳态风速的仿真结果相似，PI与LQG控制算法只能抑制低频分量，而PI-R控制算法不仅可以抑制低频分量，而且可以抑制3p分量。但是受其他随机频率分量的干扰，PI-R控制算法对3p分量的控制效果比稳态风速下的控制效果要差。这些随机频率的分量主要是由随机的风况造成的。因此对于随机分量的抑制，需要基于更加准确的风速测量技术。篇幅所限，这一部分内容不在本文的讨论范畴中，具体请参见文献［16］。

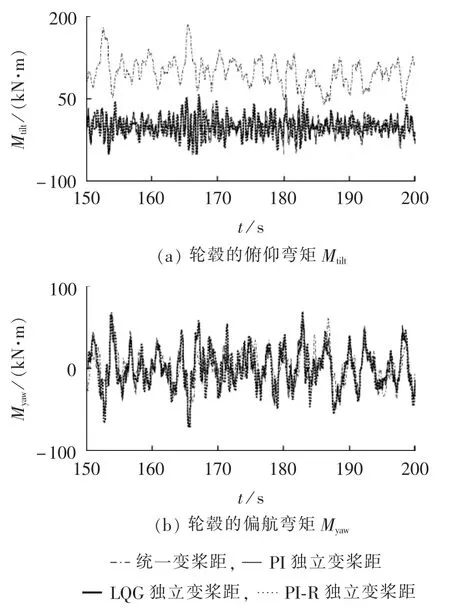
图5 10%湍流风速下不同控制算法的仿真波形Fig.5 Simulative results of different control algorithms under 10%turbulent wind speed

图6 10%湍流风速下轮毂俯仰弯矩和偏航弯矩的FFT分析Fig.6 FFT analysis of tilt and yaw moments for hub under 10%turbulent wind speed

4 结论

本文基于对风轮所承受的不平衡载荷频率特性的分析，提出了一种用于降低风轮所承受不平衡载荷的PI-R独立变桨距控制算法，其中PI控制器用于抑制不平衡载荷的低频分量，而R控制器用于抑制高频分量。采用FAST软件进行时域仿真，并对仿真结果进行频域分析，验证了控制策略的有效性。仿真结果表明，所提控制算法在传统PI控制算法的基础上，进一步降低了风轮所承受的不平衡载荷，从而有助于提高风电机组设备的可靠性，延长其使用寿命。

［1］刘桦.风电机组系统动力学模型及关键零部件优化研究［D］.重庆：重庆大学，2009.LIU Hua.Study on systematic dynamic model and key part optimization analysis for wind turbine［D］.Chongqing：Chongqing University，2009.

［2］接勐.风力发电机组载荷控制的研究［D］.乌鲁木齐：新疆农业大学，2006.JIE Meng.The research of load control in wind turbine ［D］.Urumchi：Xinjiang Agricultural University，2006.

［3］王晓东.大型双馈风电机组动态载荷控制策略研究［D］.沈阳：沈阳工业大学，2011.WANG Xiaodong.Research on dynamic load control strategy of large scale double feed wind turbine ［D］.Shenyang：Shenyang University of Technology，2011.

［4］BOSSANYI E A.Wind turbine control for load reduction ［J］.Wind Energy，2003，6（3）：229-244.

［5］李辉，杨超，胡姚刚，等.抑制风力机疲劳载荷的直接比例谐振独立变桨控制策略［J］.电力自动化设备，2016，36（3）：79-85.LI Hui，YANG Chao，HU Yaogang，et al.Direct PR individual pitch control for wind turbine fatigue load mitigation［J］.Electric Power Automation Equipment，2016，36（3）：79-85.

［6］BOSSANYI E A.Individual blade pitch control for load reduction［J］.Wind Energy，2003，6（2）：119-128.

［7］林勇刚，李伟，陈晓波，等.大型风力发电机组独立桨叶控制系统［J］.太阳能学报，2005，26（6）：780-786.LIN Yonggang，LI Wei，CHEN Xiaobo，et al.The research on large scale wind turbine individual blade pitch control system［J］.Acta Energiae Solaris Sinica，2005，26（6）：780-786.

［8］LARSEN T J，MADSEN H A，THOMSEN K.Active load reduction using individual pitch，based on local blade flow measurements［J］.Wind Energy，2005，8（1）：67-80.

［9］STOL K A，ZHAO W，WRIGHT A D.Individual blade pitch control for the Controls Advanced Research Turbine（CART）［J］.Journal of Solar Energy Engineering，2006，128（4）：498-505.

［10］BIR G.Multi-blade coordinate transformation and its application to wind turbine analysis［R］.Reno，Nevada，USA：NREL，2008.

［11］ENGELEN T G V，HOOFT E L V D.Individual pitch control inventory［R］.［S.l.］：ECN，2005.

［12］龚文明，胡书举，许洪华.一种适用于大型风电场实时仿真的双馈风力发电机响应模型［J］.电力自动化设备，2014，34（4）：114-119.GONG Wenming，HU Shuju，XU Honghua.Response model of DFIG for real-time simulation of large-scale wind farms［J］.Electric Power Automation Equipment，2014，34（4）：114-119.

［13］ENGELEN T G V.Design model and load reduction assessment for multi-rotational mode individual pitch control（higher harmonics control）［R］.Athens，Greece：ECN，2006.

［14］BOSSANYI E A.Further load reductions with individual pitch control［J］.Wind Energy，2005，8（4）：481-485.

［15］KANEV S K，ENGELEN T G V.Exploring the limits in individual pitch control［R］.Marseille，France：ECN，2009.

［16］BURTON T，SHARPE D，JENKINS N，et al.Wind energy handbook［M］.［S.l.］：John Wiley & Sons，2001：385-416.