适用于多端柔性互联的交直流配电网潮流计算方法

彭 克，张新慧，陈 羽

（山东理工大学 电气与电子工程学院，山东 淄博 255000）

0 引言

目前我国配电网主要采用交流电网作为供电载体，交流配电网运行技术成熟，控制和保护机理相对清晰。但随着交流电网规模的扩大、电压等级的提高，复杂交流互联电网的短路容量不断增大，其运行控制过程愈发复杂，系统的安全稳定问题影响越来越严重。同时，随着电动汽车、分布式电源（如光伏）和LED照明等直流设备的大规模接入，交流电网由于电能变换环节多，供配电的效率受到影响。

近年来的研究成果表明［1-2］，基于柔性直流技术的交直流混合配电网更适合现代城市配电网的发展。交直流混合配电网可更好地接纳分布式电源和直流负荷，缓解城市电网站点走廊有限与负荷密度高的矛盾，同时在负荷中心提供动态无功支持，提高系统安全稳定水平并降低损耗。交直流混合配电网是配电网的一个重要发展趋势，可以有效提升城市配电系统的电能质量、可靠性与运行效率。

目前，交直流配电网的研究还存在大量的理论与技术问题有待解决［3-6］。在潮流控制方面，大多采用与柔性直流输电系统相似的控制策略［7-9］，文献［10］借鉴了柔性直流输电技术的控制策略并提出了直流配电网的4种控制模式，即直流稳压控制、直流有功控制、交流稳压控制及交流频率控制；文献［11］采用多端柔性直流输电技术的电压控制方式对直流配电网的多个换流器进行控制，并基于负荷与发电平衡的基本原理，提出了一种新的电压控制策略，取得了良好的效果。为达到多电源参与功率调节的目的，下垂控制被应用到换流器的控制系统中，用以协调多个换流器的功率输出［12-15］。

计及上述控制策略的潮流计算，在高压直流电网中开展较多，如文献［16-18］针对传统换流站在不同控制方式下的潮流计算展开了研究，但基于全控型电力电子器件的多端柔性直流系统是未来的发展趋势，因此传统换流站的潮流模型及算法不再适用于现代交直流配电网；文献［19］给出了多端VSC-HVDC的潮流计算模型，并基于定电压控制策略给出了交直流解耦的简化计算方法，但当采用下垂控制时，直流电压不再按照固定指令输出，交直流之间有较密切的耦合关系，因而该方法不适用于采用下垂控制的多端互联系统；文献［20］在多端直流输电系统中计及了电压-功率（U-P）以及电压-电流（U-I）不同的下垂特性，并采用牛顿法进行统一迭代计算，但牛顿法对初值较为敏感，如果初值选取不合适算法会出现不收敛的情况，此外，配电系统中由于R/X比值较大，将牛顿法直接应用于配电系统中容易形成病态方程，导致算法难以收敛；文献［21］针对配电网的辐射状特征采用了前推回代算法，但该算法对环网及多分布式电源的处理能力较弱；文献［22］采用Zbus高斯算法对交直流微电网的潮流计算展开研究，对三相不平衡的配电网具有较好的适应性，但该算法需要将平衡节点与其他节点分离计算，当采用下垂控制时，如果功率波动较大，很容易造成平衡节点的电压波动过大，导致潮流计算不收敛。

针对上述问题，本文提出了一种改进的Zbus高斯算法，通过预先给定的下垂控制曲线分步实现换流器的功率及直流电压更新，解决了常规高斯算法由于平衡节点与其他节点分离计算导致的算法不收敛问题。首先根据下垂曲线给定的直流电压参考值求解一次交直流潮流，确定功率稳态计算点；然后根据功率稳态点按照下垂曲线更新直流电压，采用新的直流电压稳定态计算点求解交直流潮流直至收敛；在改进的IEEE 123节点算例上对算法进行测试，验证本文算法的有效性和正确性。

1 交直流配电网潮流控制方法

从网络接线方式而言，柔性直流配电网的基本拓扑结构主要有放射状、两端配电及环状多端配电等，放射状网络相对环状及两端配电网络供电可靠性较低［1］。图1为多端环状直流配电网典型结构。直流配电网更利于直流型分布式电源的接入，可为直流负荷就地提供功率支撑，储能装置可以实现功率的就地平衡，但受制于容量及造价，很难作为交直流配电网潮流控制的主要手段，更多地还是由交流配电网提供功率支撑，通过换流器柔性互联的方式对潮流进行控制，可同时实现交流潮流及直流潮流的控制，其关键取决于换流器的控制，交直流配电网换流器一般具有如表1所示的典型控制方式［21］。

图1 多端环状直流配电网拓扑Fig.1 Topology of multi-terminal ringlike DC distribution network

表1 换流器控制类型Table1 Types of converter control

直流电压的稳定是潮流控制的根本目的，图1中给出了2种不同的电压控制方式：曲线①为恒压控制，维持功率输出的同时保持电压恒定，相当于直流系统的平衡节点，但各换流器之间无法协调控制；曲线②为下垂控制，根据有功功率与直流电压的线性关系，通过下垂系数协调不同换流器的功率输出，典型的下垂曲线可由式（1）表述［17］。

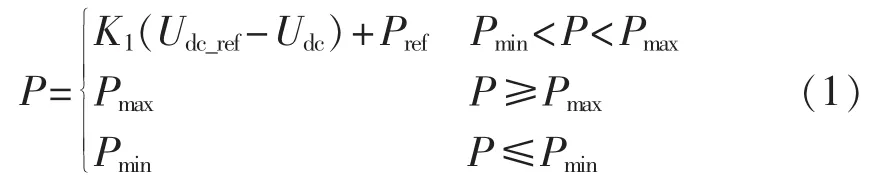
其中，Pref为功率参考值；Udc_ref为直流电压参考值；P与Udc分别为待求功率与直流电压；K1为下垂系数；Pmax与Pmin分别为整流器与逆变器的最大输出功率，正功率表示换流器工作于整流状态，负功率表示换流器工作于逆变状态。在下垂系数、功率参考值及直流电压参考值确定后，下垂曲线即可确定，直流电压即可按照该曲线受控，进而可以求取输出功率。

对式（1）进行变换，记 K=1/K1，则图 1 所示下垂曲线可化为：

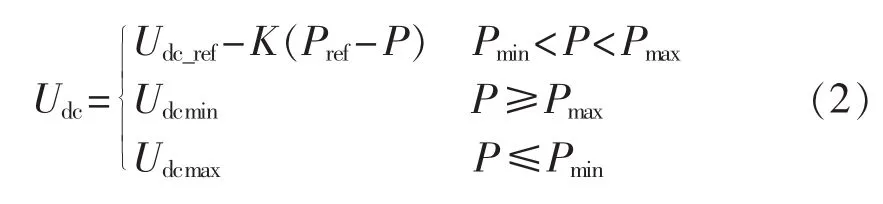
2 算法设计

交流配电网的潮流计算方法有牛顿法、Zbus高斯算法、前推回代法等。其中Zbus高斯算法是以系统节点导纳矩阵为基础的一种潮流算法，原理比较简单，要求的内存量也比较小，相比前推回代法对环状网络的求解具有较大的优势，虽然是一阶收敛的算法，但具有接近牛顿法的收敛速度和收敛特性，对于一般的配电系统具有较好的适应性。

采用Zbus高斯算法时，配电系统节点电压方程可以写成如下形式：

其中，I为节点电流注入向量；U为节点电压向量；Y为节点导纳矩阵。如果将配电系统的平衡节点和其他节点分离，则可以将系统方程写为：

其中，I1、U1分别为平衡节点的电流和电压向量；I2、U2分别为其他节点的电流和电压向量。

对配电系统而言，一般平衡节点电压U1是给定的，如果系统负荷节点注入电流I2是已知的恒定电流，则可求出系统中除平衡节点外其他节点的电压，如下式所示：

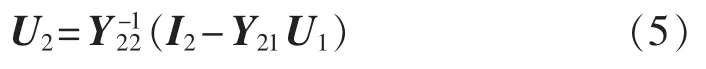
若系统负荷节点的负荷包含恒定功率成分，可以用估计电压下的等值电流注入来代替，节点电流注入向量I2成为节点电压向量U2的函数。因而有：

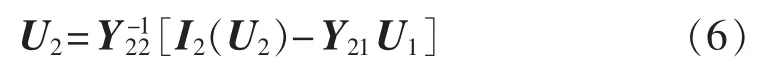
2.1 算法流程

由式（6）可以看出，采用Zbus高斯算法求解潮流时，需要将平衡节点与其他节点分离计算，采用下垂控制时，如果功率波动较大，很容易造成平衡节点电压波动过大，导致潮流迭代计算不收敛，为此本文提出一种改进的Zbus高斯算法，采用如图2所示的分步更新功率与直流电压的方法，其具体流程如下。

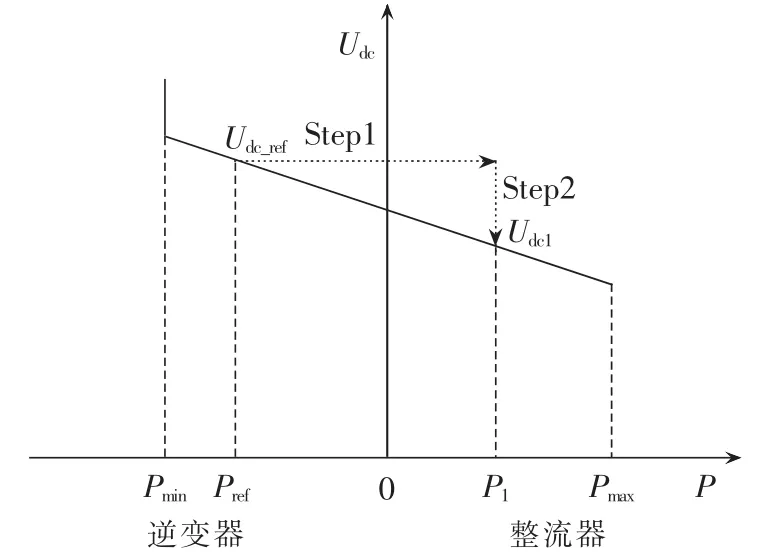
图2 换流器下垂控制处理方法Fig.2 Processing steps of converter droop control

（1）由输入数据 Pref、Udc_ref、K 得到下垂曲线。

（2）考虑到直流系统中无功功率为0，先将换流器视作（Udc_ref，Q）节点计算一次直流潮流，其中Q=0，即经过图2中Step1得到潮流收敛后的有功功率P1。

（3）将P1代入下垂曲线，更新该功率对应的直流电压Udc1，即图2所示Step2。

（4）将换流器视作（Udc1，Q）节点进行交直流求解，直至潮流收敛。

以第k+1次迭代过程为例给出具体计算步骤。

a.取换流器电压利用第 k 次的注入电流求解第k+1次直流系统的节点电压［18］：

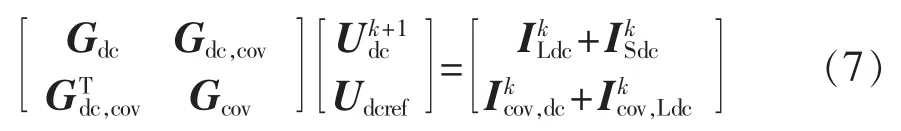
其中，Gdc为非换流器节点的电导；Gdc，cov为直流系统与换流器耦合部分的电导；Gcov为换流器电导为第k+1次迭代过程中的直流系统电压为第k次迭代过程中的直流负荷电流；为第k次迭代过程中的直流电源电流；为第k次迭代过程中的换流器电流为第k次迭代过程中的换流器所载负荷电流。

b.计算换流器的直流电流

c.求解换流器直流功率

d.更新换流器直流电压，若功率不越限，则=否则功率取极大值或极小值。

e.取换流器更新后的直流电压重新求解下式：

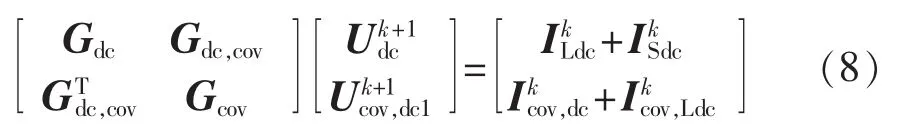
f.计算换流器直流功率

g.忽略换流器损耗，取换流器交流功率

h.由换流器交流功率计算交流电流

i.求解交流节点电压方程：

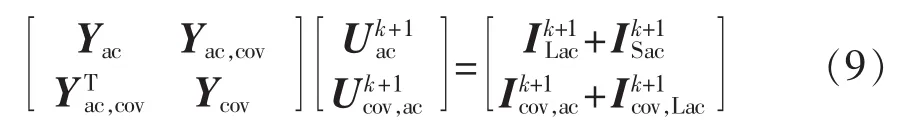
j.判断直流系统及交流系统是否收敛，即：

其中，ε为给定的潮流迭代误差。若收敛则退出计算，否则返回步骤（1）继续计算。

2.2 算法收敛性分析

常规高斯算法中平衡节点与其他节点分离计算，由式（6）可知，对直流网络求解时具有如下迭代格式：

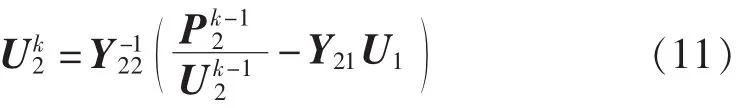
其中为第k-1次迭代的非平衡节点的有功功率；为第k-1次迭代的非平衡节点的电压。

该迭代格式在求解未采用下垂控制的配电网潮流时（包括交直流配电网的迭代）具有较好的收敛性，前期已有大量研究，本文不再做详细讨论，下面主要分析采用下垂控制时的收敛性。

换流器采用下垂控制时U1需参与迭代计算：

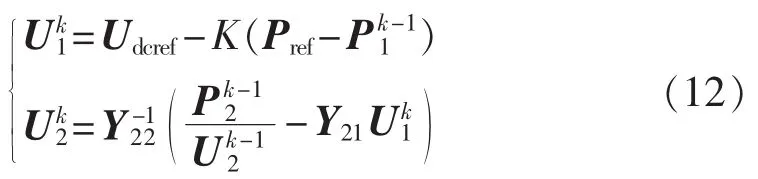
其中，为第k-1次迭代的平衡节点的有功功率。

若迭代收敛则需满足：

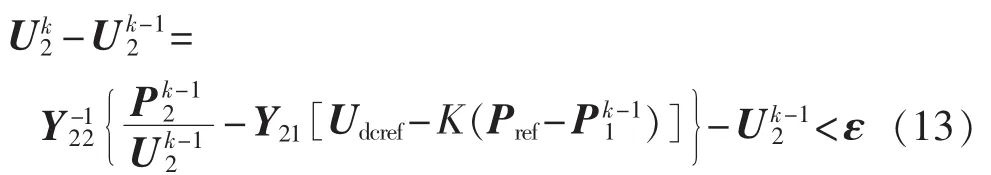
比较式（13）与式（11）可知，假设式（11）收敛，则式（13）需多满足如下收敛条件才会收敛。

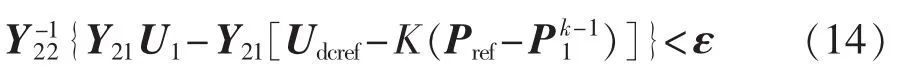
即：

由式（15）可以看出，要保证其收敛性，有功功率波动是有上限值的（这也同上文所述“如果功率波动较大，很容易造成平衡节点电压波动过大，导致潮流迭代计算不收敛”是一致的），主要与下垂系数、直流电压参考值以及初始值等相关（ε取很小的数值时可忽略的值）。

而本文算法对采用下垂控制的平衡节点采用分步计算，即先将换流器视作（Udc_ref，Q）节点进行一次求解，用所求得的功率直接根据下垂曲线更新U1，因而平衡节点并不直接参与迭代，在中间计算过程中是一个常值，整个计算过程仍然以式（11）的迭代格式计算，其收敛性不受式（15）条件限制，收敛性与未采用下垂控制的高斯算法一致，保证了采用下垂控制时算法的良好收敛性。

此外，由于双向换流器潮流方向并不固定，在潮流计算过程中下垂曲线设计的不同可能导致功率流向的不同，因此在计算过程中需要判断换流器的工作状态，以切换换流器的工作模式。本文所设计算法流程如图3所示。

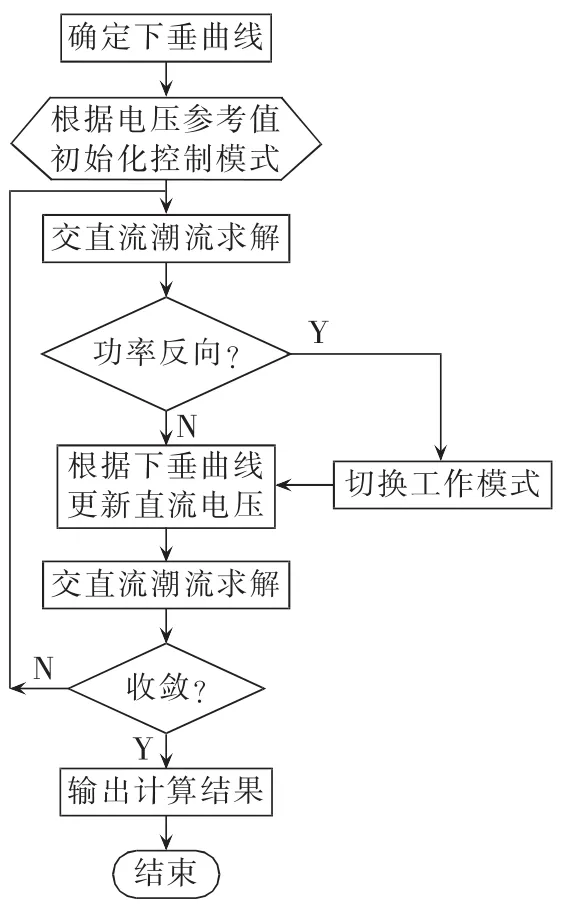
图3 算法流程Fig.3 Flowchart of algorithm

3 算例测试

本文在文献［23］改进的IEEE 123节点算例上对所提混合潮流计算方法进行测试与分析，该算例包含2个直流配电网络，其中直流配电网2基于三端直流拓扑实现，即通过3个换流器向直流配电网供电，同时网络中含有丰富的分布式电源及直流负荷，算例详细参数见文献［23］。本文算法基于天津大学所开发的PFDG（Power Flow for Distributed Generation）软件实现。同时为验证本文算法的正确性，在DIgSILENT仿真软件中搭建该算例进行结果校验。

3.1 场景1：恒压控制

直流配电网2中3个换流器均采用恒压控制，直流电压目标值设定为1.0 p.u.，潮流计算结果如表2所示，且与DIgSILENT计算结果基本一致。

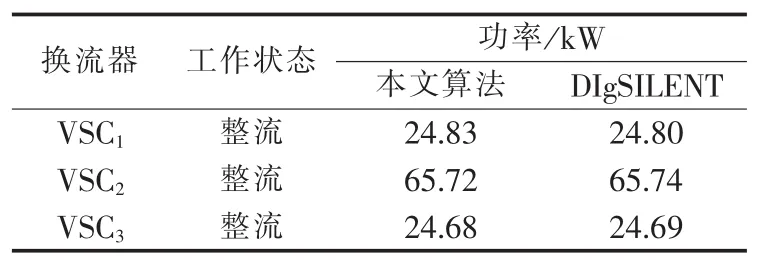
表2 恒压控制潮流计算结果Table2 Results of power flow calculation for constant voltage control

3.2 场景2：下垂控制

直流配电网2中3个换流器均采用下垂控制，下垂系数及潮流计算结果见表3，且与DIgSILENT计算结果基本一致。

表3 下垂控制潮流计算结果Table3 Results of power flow calculation for droop control

3.3 场景3：换流器工作模式转换

将VSC2换流器下垂系数继续减小至2%，此时VSC2工作模式转换至逆变状态，潮流计算结果如表4所示，且与DIgSILENT计算结果基本一致。

表4 换流器工作模式转换潮流计算结果Table4 Results of power flow calculation for converter operating mode changeover

通过比较表2与表3结果可知，3个换流器均工作于整流状态向直流配电网输送功率，总共传输有功功率115.23 kW，采用下垂控制时，3个换流器可根据给定的下垂曲线实现直流电压受控，进而控制换流器功率输出，实现换流器的负荷均摊。由此可以看出，相对于恒压控制，采用下垂控制时，换流器的功率输出更为灵活。而表4所示结果表明，换流器可根据下垂系数的改变切换工作模式，当转换至逆变工作状态时，可向区外供电，运行方式也更为灵活。

3.4 算法收敛性分析

为验证本文算法的有效性，在场景2计算条件下表5给出了其与常规高斯算法的收敛性能比较。由于算例中包含PV节点，因而存在两层迭代计算。当采用恒压控制时，本文算法与常规高斯算法收敛性能一致；当采用下垂控制时，常规高斯算法不收敛，而本文算法由于分步更新功率与直流电压，保证了算法的收敛性。

表5 算法收敛性比较Table5 Comparison of algorithm convergency among algorithms

通过以上结果可以看出，本文算法较好地计及了下垂控制特性，实现了换流器对负荷的均摊；对换流器工作状态的切换也具有较好的适应性，可根据下垂系数自适应转换工作模式；在收敛性上也优于常规高斯算法，但需要指出的是，由于本文算法分步更新功率与直流电压，导致内循环迭代次数较多，这也是后续研究需要解决的问题。

4 结论

本文提出一种适用于采用下垂控制的多端互联交直流配电系统的潮流计算方法，通过预先给定的下垂控制曲线计算换流器的功率及直流电压，实现换流器的负荷均摊，在改进的IEEE 123节点算例上对本文算法进行测试，验证本文算法的有效性和正确性。本文算法是基于高斯算法对下垂曲线进行分步处理，后续将深入研究，考虑高斯与牛顿算法的混合求解进行统一迭代，进一步加强算法的收敛性能。

［1］宋强，赵彪，刘文华.智能直流配电网研究综述［J］.中国电机工程学报，2013，33（25）：9-19.SONG Qiang，ZHAO Biao，LIU Wenhua.An overview of research on smart DC distribution power network［J］.Proceedings of the CSEE，2013，33（25）：9-19.

［2］雍静，徐欣，曾礼强，等.低压直流供电系统研究综述［J］.中国电机工程学报，2013，33（7）：42-52.YONG Jing，XU Xin，ZENG Liqiang，et al.A review of low voltage DC power distribution system ［J］.Proceedings of the CSEE，2013，33（7）：42-52.

［3］江道灼，郑欢.直流配电网研究现状与展望［J］.电力系统自动化，2012，36（8）：98-104.JIANG Daozhuo，ZHENG Huan.Research status and developing prospect of DC distribution network［J］.Automation of Electric Power Systems，2012，36（8）：98-104.

［4］王丹，毛承雄，陆继明，等.直流配电系统技术分析及设计构想［J］.电力系统自动化，2013，37（8）：82-88.WANG Dan，MAO Chengxiong，LU Jiming，et al.Technical analysis and design concept of DC distribution system［J］.Automation of Electric Power Systems，2013，37（8）：82-88.

［5］康青，马晓春，叶卫华.直流配电网关键技术及展望［J］.电气自动化，2014，36（1）：5-7，23.KANG Qing，MA Xiaochun，YE Weihua.Key technology of DC distribution network and its prospect［J］.Electrical Automation，2014，36（1）：5-7，23.

［6］PARK J S，CHOI J H，GU B G，et al.Feasibility study of DC electrical distribution system［C］∥Proceedings of the 8th International Conference on Power Electronics and ECCE Asia，2011.Jeju，Korea：［s.n.］，2011：2935-2938.

［7］NAKAJIMA T，IROKAWA S.A control system for HVDC transmission by voltage sourced converters［C］∥IEEE PES Summer Meeting.Edmonton，Alberta，Canada：［s.n.］，1999：1113-1119.

［8］DIERCKXSENS C，SRIVASTAVA K，REZA M，et al.A distributed DC voltage control method for VSC MTDC systems［J］.Electric Power Systems Research，2012，82：54-58.

［9］BEERTEN J，COLE S，BELMANS R.Generalized steady-state VSC MTDC model for sequential AC/DC power flow algorithms［J］.IEEE Transactions on Power Systems，2012，27（2）：821-829.

［10］LI Guangkai，LI Gengyin，ZHAO Chengyong，et al.Research on voltage source converter based DC distribution network ［C］∥Second IEEE Conference on Industrial Electronics and Applications，2007.Harbin，China：［s.n.］，2007：1927-1932.

［11］MAHMOODI M，GHAREHPETIAN G B，ABEDI M，et al.A suitable control strategy for source converters and a novel loadgeneration voltage control scheme for DC voltage determination in DC distribution systems［C］∥First International Power and Energy Conference，2006.Putrajaya，Malaysia：［s.n.］，2006：363-367.

［12］马骏超，江全元，余鹏，等.直流配电网能量优化控制技术综述，电力系统自动化，2013，37（24）：89-96.MA Junchao，JIANG Quanyuan，YU Peng，et al.Survey on energy optimized control technology in DC distribution network ［J］.Automation of Electric Power Systems，2013，37（24）：89-96.

［13］杨文博，宋强，朱喆，等.基于直流内电势控制的MMC多端直流输电系统最优下垂控制［J］.电力自动化设备，2016，36（10）：51-59.YANG Wenbo，SONG Qiang，ZHU Zhe，et al.Optimal droop control based on direct DC internal potential control for MMCMTDC system［J］.Electric Power Automation Equipment，2016，36（10）：51-59.

［14］杜翼，江道灼，尹瑞，等.直流配电网拓扑结构及控制策略［J］.电力自动化设备，2015，35（1）：139-145.DU Yi，JIANG Daozhuo，YIN Rui，et al.Topological structure and control strategy of DC distribution network［J］.Electric Power Automation Equipment，2015，35（1）：139-145.

［15］GOMIS-BELLMUNT O，LIANG J，EKANAYAKE J，et al.Voltagecurrent characteristics of multiterminal HVDC-VSC for offshore wind farms［J］.Electric Power Systems Research，2011，81：440-450.

［16］陆进军，黄家裕.电力系统多端直流（MTDC）潮流算法改进［J］.电力系统及其自动化学报，2000，12（5）：4-6，18.LU Jinjun，HUANG Jiayu.An improved multi-terminal HVDC power flow method［J］.Proceedings of the CSU-EPSA，2000，12（5）：4-6，18.

［17］刘崇茹，张伯明，孙宏斌，等.多种控制方式下交直流系统潮流算法改进［J］.电力系统自动化，2005，29（21）：25-31.LIU Chongru，ZHANG Boming，SUN Hongbin，et al.Advanced AC-DC power flow algorithm considering various controls ［J］.Automation of Electric Power Systems，2005，29（21）：25-31.

［18］邱革非，束洪春，于继来.一种交直流电力系统潮流计算实用新算法［J］.中国电机工程学报，2008，18（5）：53-57.QIU Gefei，SHU Hongchun，YU Jilai.New practicable algorithm dealing with AC/DC power flow calculation［J］.Proceedings of the CSEE，2008，18（5）：53-57.

［19］陈谦，唐国庆，王浔.多端VSC-HVDC系统交直流潮流计算［J］.电力自动化设备，2005，25（6）：1-6.CHEN Qian，TANG Guoqing，WANG Xun.AC-DC power flow algrithom for multi-terminal VSC-HVDC systems［J］.Electric Power Automation Equipment，2005，25（6）：1-6.

［20］WANG Wenyuan，BARNES M.Power flow algorithms for multiterminal VSC-HVDC with droop control［J］.IEEE Transactions on Power Systems，2014，29（4）：1721-1730.

［21］王守相，江兴月，王成山.含风力发电机组的配电网潮流计算［J］.电网技术，2006，30（21）：38-42.WANG Shouxiang，JIANG Xingyue，WANG Chengshan.Powerflow analysis of distribution network containing win d power generators［J］.Power System Technology，2006，30（21）：38-42.

［22］王成山，孙充勃，彭克，等.微电网交直流混合潮流算法研究［J］.中国电机工程学报，2013，33（4）：8-15.WANG Chengshan，SUN Chongbo，PENG Ke，et al.Study on ACDC hybrid power flow algorithm for microgrid［J］.Proceedings of the CSEE，2013，33（4）：8-15.

［23］孙充勃.含多种直流环节的智能配电网快速仿真与模拟关键技术研究［D］.天津：天津大学，2015.SUN Chongbo.Study on key technologies of fast simulation and modeling for smart distribution grid with multi-DC components［D］.Tianjin：Tianjin University，2015.学出版社，2007：12-14..