基于属性约简的应用服务器优化算法改进

李佳泽， 王长忠

(1.中国核科技信息与经济研究院, 北京 100048; 2.渤海大学,辽宁 锦州 121000)

基于属性约简的应用服务器优化算法改进

李佳泽1， 王长忠2

(1.中国核科技信息与经济研究院, 北京 100048; 2.渤海大学,辽宁 锦州 121000)

优化参数配置是优化应用服务器性能的重要方面;基于传统参数调节的优化策略耗时耗力缺乏系统性和规律性;利用模块化思想针对目标决策函数对应用服务器参数进行分类，可构建条件属性约简模型;基于属性约简的应用服务器优化算法，可去除对于目标决策函数相对不重要的参数，并获得相对重要的参数，从而达到锁定目标重点调节，快速提高系统性能的目的;现有的约简模型优化算法多基于经典粗糙集理论，在等价关系的基础上构造分类，容易造成大量的信息破坏和流失;文章通过拓展等价关系到一般二元关系，利用广义粗糙集理论改良了基于模块化思想和属性约简模型的应用服务器优化算法，通过定义辨识函数对条件属性进行约简，再结合依赖度计算，得到最终目标参数。

服务器优化；参数模块；一般二元关系；属性约简

0 引言

信息化背景下，企业应用系统性能的好坏关系着企业信息化水平的高低。性能良好的应用系统，可在服务器高负载的情况下保持较高的吞吐量。而实现此目标，要求应用服务器能保持较高的可用性。但随着企业应用系统的增加、应用范围的扩大以及应用数据和服务时间的增长，应用系统性能会有所下降，系统维护人员需要根据具体情况对应用系统进行适当的优化。传统的优化方法主要分为两种。一种是通过对应用程序进行分析，根据程序运行结果分析应用系统性能下降的原因，其方法体现为代码模式的改进[1-2]。此方法要求维护人员必须充分了解代码。然而企业应用系统的维护通常并非由开发人员负责，维护人员往往是应用部门的普通人员，不具备相应的专业水平。所以，基于应用程序调节的优化方法比较适用于应用系统的部署和测试阶段。另一种优化方法是针对系统硬件，即对服务器进行调节，要么基于对服务器的技术文档分析，从而对服务器和系统应用平台进行参数调节[3-4]，要么利用成熟的优化工具分析系统性能然后调节[5]。这些优化方法成功与否，很大程度上取决于运行维护人员的经验，缺乏系统性和规律性。刘岩、王正方等人根据经典的J2EE模型架构分析，利用参数模块化思想，针对应用服务器的相关参数，提出了一种ARBPMTAS(attributes reduction basingon parameters modulein tuning application server)优化算法[6]，但此算法的约简模型是建立在等价关系的基础上，在实际计算会带来一定的信息破坏和流失。

本文通过将等价关系计算拓展到一般二元关系计算，构造广义粗糙集理论下的决策系统和条件属性约简模型，通过定义可辨识域、辨识矩阵和辨识函数对条件属性集进行约简，再结合决策属性对条件属性的依赖度计算，提出了一种改良的基于模块化思想和属性约简模型的应用服务器优化算法，即基于一般二元关系决策系统属性约简模型的应用服务器优化算法。文章最后，用改良后的算法对文献[6]的实例进行了重新计算，得到了更为精确的计算结果。

1 相关知识

1.1 一般二元关系

二元关系(binary relation)用于讨论两个数学对象的联系。设R是集合A上的一个二元关系，若R满足以下特殊性质，

自反性：∀a∈A,=>(a,a)∈R

对称性：(a,b)∈R∧a≠b=>(b,a)∈R

传递性：(a,b)∈R,(b,c)∈R=>(a,c)∈R

则称R是定义在A上的一个等价关系；若R只满足只自反性和传递性，则等价关系拓展为优势关系。此外，还有偏序关系、相融关系等，这些都是具有一定数学特性的特殊二元关系。如果R没有任何数学特性的约束，此时的R被称为一般二元关系。一般二元关系是所有特殊二元关系的拓展。

1.2 一般二元关系下的属性约简模型[7]

设U为参数域，R⊆U×U是U上的二元关系，这时，序对(U,R)称为广义近似空间；Rs:U→2U为集值函数。对于参数x∈U，称集Rs(x)={y∈U:(x,y)∈R}为参数x关于关系R的后继邻域。对于U上的一簇二元关系R={R1,R2,...,Rn}，引入决策等价关系D，称U/D={[x]D:x∈U}是参数域U上相对于关系R的决策划分，这时，我们就构造了一种决策系统，记为(U,R,D)。

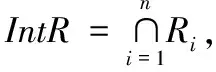
对于任意的参数集X⊆U，P⊆R，X关于R的下近似可定义为：

⊆X

且(IntR)s(x)≠φ}

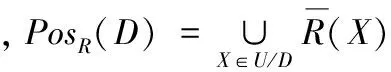
在决策系统(U,R,D)中，对于Ri∈R，当且仅当PosR(D)=Pos{R-{Ri}}(D)且NulR(D)=Nul{R-{Ri}}(D)时，Ri相对于D是R中不必要的。对于设P⊆R，如果P中每一个元素相对于D都是P中必要的。

称P相对于D是R的一个约简。当:

Α={(x,y)|x∈NulR(D),y∈U}∪

{(x,y)|x∈PosR(D),y∈U且d((IntR)s(x))≠d(y)}

称Α为D关于R的可辨识域。(U,R,D)的辨识矩阵记为(cij)，对∀xi,xj∈U

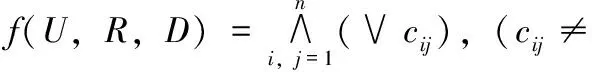
对于P⊆R，如果P是满足P∩cij≠φ(cij≠φ;i,j≤n)的最小子集，则认为P相对于D是R的一个约简。

以上描述的属性约简模型用于机器故障分析效果良好，通过计算可以约简掉相对于决策属性不必要的条件属性，达到故障排除的目的，也可以通过得到必要属性，达到锁定重点目标的目的。下面我们再引入属性间依赖程度的概念，进一步描述属性间的关系。

对于属性集R⊆CP⊆D，称:

为P对R的依赖程度[8]。

2 基于属性约简的应用服务器优化改进算法的设计

ARBPMTAS算法选用WebLogic作为WEB容器，结合参数模块化思想，将每个参数模块看作条件属性集R，用户并发访问系统时系统的相应时间作为决策系统D，针对目标决策函数对应用服务器的参数进行等价分类，构建了条件属性集的约简模型，通过计算决策属性对每个条件属性的依赖性，直到正域相等结束计算，得到了属性约简集。这种基于属性约简的计算方法有效去除了对于目标决策函数相对不重要的参数，并获得了相对重要的参数，然后锁定目标参数重点调节，在快速提高系统性能方面得到了良好的实践效果。但是，由于这种约简模型建立在等价关系的基础上，在现实中获取到的实值连续型数据样本中，关系的计算只能被离散化描述，会带来信息破坏和流失，影响计算效果。

把建立在等价关系这种特殊二元关系的计算拓展到一般二元关系定义相应的计算，使计算过程得到了更贴近实际的描述，可以有效减少计算过程中的信息流失。属性约简主要通过研究条件属性与决策属性的关系，按照一定规则约简掉相对决策属性不必要的条件属性。如1.2介绍的属性约简模型是基于一般二元关系的粗糙集理论(也称广义粗糙集理论)构建的，首先在传统粗糙集理论上下近似的概念基础上引入正域、后继邻域等概念，进而描述出什么样的条件属性相对于决策属性是可辨识的，根据辨识性规则实现属性约简，杜晓昕、徐慧等人通过定义决策属性对条件属性的依赖度，根据依赖度大小来判断属性的必要性[8]。

本文以定义的广义粗糙集理论下的属性约简模型[7]作为计算基础，结合文献[6]的计算思路，提出改进的基于模块化思想和属性约简模型的应用服务器优化算法如下：

(1)描述样本数据在条件属性下的关系，对∀xi,xj∈U，xj与xi有关系，记为(xi,xj)；

(3)对于可辨识域A，若(xi,xj)∉A，结束计算，重复第2步；若(xi,xj)∈A，则记Rs为辨识矩阵cij的第(i,j)元；

(4)若cij=φ;i,j≤n结束计算,重复第3步;若cij≠φ;i,j≤n计算P∩cij≠φ的最小子集P即是R的一个约简；

(5)计算P对R的依赖度γR(P)取最大值，此时的P为目标参数。

3 实例分析

选取文献[6]的样本数据(见表1)，用第2节的优化算法重新计算。

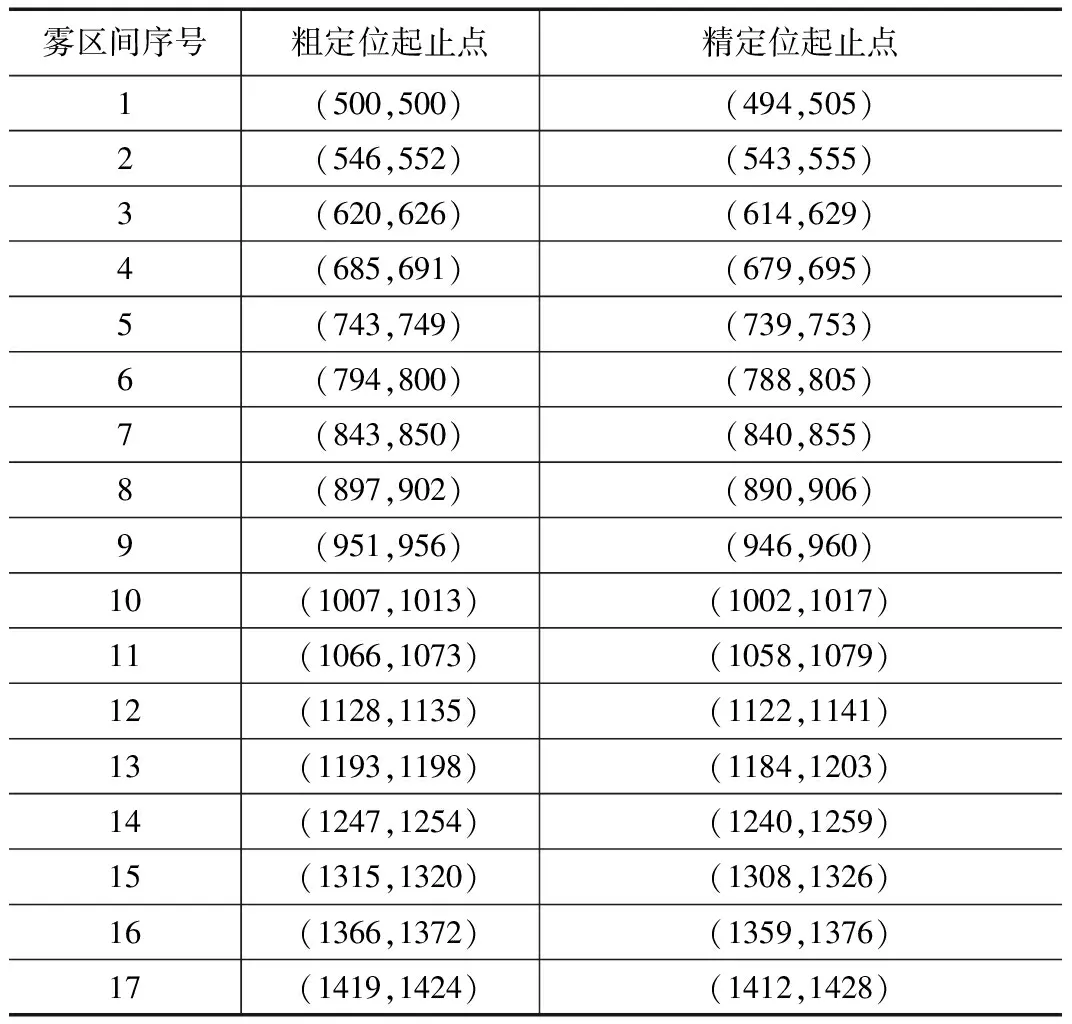
表1 自运行端参数决策系统[6]

注：系统状态表示据系统响应时间判断是否满足要求，是Y否N

可见，该数据样本除了存在等价关系，还存在优势关系、偏序关系等二元关系，用以一般二元关系为基础的计算方法能更好的挖掘数据信息。下面我们用本文提出的基于模块化思想和属性约简模型的应用服务器优化改进算法进行计算：

记U={x1,x2,x3,x4,x5,x6,x7,x8,x9,x10}，D={Y,N}系统状态可描述为:

U/D={X1={x1,x4,x5,x8,x10}(满足要求)

X2={x2,x3,x6,x7,x9}(不满足要求)}

记关系属性集R={R1,R2,R3,R4,R5}，对∀xi,xj∈U，当xi≠xj记作(xi,xj)

可整理二元关系属性集如下：

R1={(x1,x2),(x1,x3),(x1,x4),(x1,x6),(x1,x7),

(x1,x8),(x1,x9),(x2,x1),(x2,x3),(x2,x5),(x2,x7),

(x2,x10),(x3,x1),(x3,x2),(x3,x4),(x3,x5),(x3,x6),

(x3,x8),(x3,x9),(x3,x10),(x4,x1),(x4,x3),(x4,x5),

(x4,x7),(x4,x10),(x5,x2),(x5,x3),(x5,x4),(x5,x6),

(x5,x7),(x5,x8),(x5,x9),(x6,x1),(x6,x3),(x6,x5),

(x6,x7),(x6,x10),(x7,x1),(x7,x2),(x7,x4),(x7,x5),

(x7,x6),(x7,x8),(x7,x9),(x7,x10),(x8,x1),(x8,x3),

(x8,x5),(x8,x7),(x8,x10),(x9,x1),(x9,x3),(x9,x5),

(x9,x7),(x9,x10),(x10,x2),(x10,x3),(x10,x4),

(x10,x6),(x10,x7),(x10,x8),(x10,x9)}R2={(x1,x4),(x1,x5),(x1,x8),(x2,x4),(x2,x5),

(x2,x8),(x3,x4),(x3,x5),(x3,x8),(x4,x1),(x4,x2),

(x4,x3),(x4,x5),(x4,x6),(x4,x7),(x4,x9),(x4,x10),

(x5,x1),(x5,x2),(x5,x3),(x5,x4),(x5,x6),(x5,x7),

(x5,x8),(x5,x9),(x5,x10),(x6,x4),(x6,x5),(x6,x8),

(x7,x4),(x7,x5),(x7,x8),(x8,x1),(x8,x2),(x8,x3),

(x8,x5),(x8,x6),(x8,x7),(x8,x9),(x8,x10),(x9,x4),

(x9,x5),(x9,x8),(x10,x4),(x10,x5),(x10,x8)}R3={(x1,x2),(x1,x4),(x1,x6),(x1,x7),(x2,x1),

(x2,x3),(x2,x4),(x2,x5),(x2,x6),(x2,x7),(x2,x9),

(x2,x10),(x3,x2),(x3,x4),(x3,x6),(x3,x7),(x4,x1),

(x4,x2),(x4,x3),(x4,x5),(x4,x6),(x4,x8),(x4,x9),

(x4,x10),(x5,x2),(x5,x4),(x5,x6),(x5,x7),(x6,x1),

(x6,x3),(x6,x4),(x6,x5),(x6,x7),(x6,x8),(x6,x9),

(x6,x10),(x7,x1),(x7,x2)(x7,x3),(x7,x5),(x7,x6),

(x7,x8),(x7,x9),(x7,x10),(x8,x2),(x8,x4),(x8,x6),

(x8,x7),(x9,x2),(x9,x4),(x9,x6),(x9,x7),(x10,x2),

(x10,x4),(x10,x6),(x10,x7)}R4={(x1,x2),(x1,x4),(x1,x6),(x1,x8),(x1,x9),

(x2,x1),(x2,x3),(x2,x4),(x2,x5),(x2,x7),(x2,x8),

(x2,x10),(x3,x2),(x3,x4),(x3,x6),(x3,x8),(x3,x9),

(x4,x1),(x4,x2),(x4,x3),(x4,x5),(x4,x6),(x4,x7),

(x4,x9),(x4,x10),(x5,x2),(x5,x4),(x5,x6),(x5,x8),

(x5,x9),(x6,x1),(x6,x3),(x6,x4),(x6,x5),(x6,x7),

(x6,x8),(x6,x10),(x7,x2)(x7,x4),(x7,x6),(x7,x8),

(x7,x9),(x8,x1),(x8,x2),(x8,x3),(x8,x5),(x8,x6),

(x8,x7),(x8,x9),(x8,x10),(x9,x1),(x9,x3),(x9,x4),

(x9,x5),(x9,x7),(x9,x8),(x9,x10),(x10,x2),(x10,x4),

(x10,x6),(x10,x8),(x10,x9)}R5={(x1,x2),(x1,x6),(x1,x9),(x1,x10),(x2,x1),

(x2,x3),(x2,x4),(x2,x5),(x2,x7),(x2,x8),(x2,x9),

(x3,x2),(x3,x6),(x3,x9),(x3,x10),(x4,x2),(x4,x6),

(x4,x9),(x4,x10),(x5,x2),(x5,x6),(x5,x9),(x5,x10),

(x6,x1),(x6,x3),(x6,x4),(x6,x5),(x6,x7),(x6,x8),

(x6,x9),(x7,x2),(x7,x6),(x7,x9),(x7,x10),(x8,x2),

(x8,x6),(x8,x9),(x8,x10),(x9,x1),(x9,x2),(x9,x3),

(x9,x4),(x9,x5),(x9,x6),(x9,x7),(x9,x8),(x9,x10),

(x10,x1),(x10,x3),(x10,x4),(x10,x5),(x10,x7),

(x10,x8)(x10,x9)}得IntR={(x2,x5),(x4,x10),(x5,x2),

(x5,x6),(x6,x5),(x10,x4)}

其中: (IntR)s(x1)=(IntR)s(x3)=(IntR)s(x7)=

(IntR)s(x8)=(IntR)s(x9)=φ

(IntR)s(x2)={x5}，(IntR)s(x4)={x10}，(IntR)s(x5)={x2,x6}，(IntR)s(x6)={x5}，

(IntR)s(x10)={x4}，则:

PosR(D)={x2,x4,x5,x6,x10}

NulR(D)={x1,x3,x7,x8,x9}

故(U,R,D)的辨识矩阵为：

辨识函数为：

f(U,R,D)=R2∧(R2∨R3∨R4∨R5)∧(R2∨R5)

∧(R1∨R3∨R4∨R5)∧(R2∨R4∨R5)∧(R3∨R5)

∧(R2∨R3)∧(R1∨R2∨R4)∧R5∧(R3∨R4∨R5)

∧(R1∨R2∨R4∨R5)∧(R2∨R3∨R4)∧R1

∧(R1∨R3∨R4)∧(R4∨R5)∧(R4∨R5)∧(R2∨R4)

∧(R1∨R4∨R5)∧(R1∨R3)∧R3∧R

=R1∨R2∨R3∨R5

可见R1R2R3R5分别是R的一个约简，R4是不必要属性在参数调节中可忽略。再计算依赖度如下：

可见，该应用系统当前状态下，决策属性D(系统响应时间)对R1(套接口读取器)的依赖程度最大，R1为重要参数，在应用服务器优化时可着重调节。此计算结果较比文献[6]更加精准的锁定了影响应用系统响应时间的服务器参数，在应用服务器优化调节中增提高了工作效率。

4 结束语

基于一般二元关系决策系统属性约简模型的应用服务器优化算法改进了已有优化方法缺乏系统性、规律性和易信息流失等弊端，通过属性约简挖掘出重点参数，达到有效优化应用服务器的目的。然而在本算法中，决策关系依然是等价关系，且属性集与决策集的从属关系也都是分明的，对于实际系统架构各模块间的参数，还存在更为复杂的关联，需要通过进一步在拓展特殊关系为一般关系、分明关系为模糊关系的基础上挖掘数据信息。

[1]VictorSafronov,ManishParashar.OptimizingWebServersUsingPageRankPrefetchingforClusteredAccesses[J].WorldWideWeb, 2002, 5(1), 25-40.

[2]ArtigesM.BEAweblogicserver8.1unleashed[M].Beijing:ChinaMachinePress, 2005.

[3]NybergG,PatrickR.MasteringBEAwebLogicserver[M].Beijing:PublishingHouseofElectronicsIndustry, 2004.

[4]OkkyungChoi,SangYongHan.PersonalizationofRule-basedWebServices[J].Sensors, 2008, 8(4).

[5]JiangGuo,LiaoYuehong,BehzadP.AsurveyofJ2EEapplicationperformancemanagementsystems[A].IEEEComputerSocietyProceedingsoftheIEEEInternationalConferenceonUniversity[C].2005, 30(3): 2-54.

[6] 刘 岩，王正方，朱云龙.参数模块和属性约简的应用服务器优化方法[J].小型微型计算机系统，2010(3)：441-445.

[7] 李佳泽，包文颖，王长忠.一般二元关系下的关系决策系统属性约简[J].模糊系统与数学，2012,26(6)：153-158.

[8] 杜晓昕, 徐 慧, 任长伟.基于粗糙集的属性约简在数据挖掘中的作用[DB/OL].中国科技论文在线, 2006.

Improved Algorithm in Tuning Application Server Based on Attribute Reduction

Li Jiaze1, Wang Changzhong2

(1.China Institute of Nuclear Information and Economy, Beijing 100048，China; 2.Bohai University, Jinzhou 121000，China)

Optimizing parameter configuration is an important way to optimize the performance of application server. The optimization strategy based on the traditional parameter adjustment is time-consuming and lacks of systematic and regularity. Based on the modular idea, the model of conditional attribute reduction can be constructed by using the target decision function to classify the parameters of the application server. The application server optimization algorithm based on attribute reduction, can remove parameters which are less important for the target decision function, and obtain the parameters of relative importance, so as to achieve the target focus adjustment, rapidly improve the performance of the system. Based on classical rough set theory, the existing reduction model optimization algorithm is constructed on the basis of equivalence relation, which is easy to cause a lot of damage and loss of information. This article through the expansion of equivalence relation to general two elements, using the generalized rough set theory to improve the application server optimization algorithm of modularization and attribute reduction model based on discernibility function are defined by the reduction of condition attributes, combined with the dependence of the calculation, obtain the final target parameters.

server optimization; parameter module; two element relation; attribute reduction

2016-12-27；

2016-12-30。

李佳泽(1986-)，女，辽宁人，硕士研究生，工程师，主要从事应用数学,软件开发系统测评等方向的研究。

1671-4598(2017)05-0255-03DOI：10.16526/j.cnki.11-4762/tp

TP

A