基于模型参考自适应PID的高压釜温度控制

王玉华,郑骁健

(中国计量大学 机电工程学院，杭州 310018)

基于模型参考自适应PID的高压釜温度控制

王玉华,郑骁健

(中国计量大学 机电工程学院，杭州 310018)

通过对某厂生产复合玻璃关键步骤“合片抽真空”的研究，发现在此过程中应用的温度控制方法简单，控制效果不理想，会产生超调、震荡等现象;为了解决在温度控制过程中出现的这些现象，提出了一种基于模型参考自适应PID的高压釜温度控制方式;首先，通过实验对高压釜釜内温度进行温度建模;然后，以此温度模型为理论依据，通过模型参考自适应控制方式对PID参数进行在线调整，即利用了PID控制使用方便、原理简单的特点，又弥补PID参数不能在线整定的缺点;通过仿真实验证明，该控制方案能够有效减少超调量，改善动态特性。

数学建模；PID控制；模型参考自适应控制；参数在线调整

0 引言

在复合玻璃的生产过程中，“合片抽真空”是其生产过程的关键步骤[1]，通常使用高压釜进行生产。在生产时，最为重要的是精确控制合片过程中压力与温度的值。本文所研究的生产工艺，是以远红外线高压釜作为生产设备[2-4]，其在复合玻璃的合片加压、加热、抽真空过程中，提供生产所需要的高温高压。

在“合片抽真空”过程中，胶片的含水率是一个重要因素，胶片与玻璃的粘结力与胶片含水率成反比，即含水率越高，胶片与玻璃的粘结力越小[5]。通过加热，既可以使胶片软化，使玻璃与胶片可以更好的粘合，又可以蒸发出胶片中的水分，增加胶片的粘结力；通过加压、抽真空，则可以抽出被蒸发的水分以及玻璃与胶片之间的空气，使胶片与玻璃通过压力更好的粘结在一起。因此，压力与温度成为影响复合玻璃质量好坏的关键因素。

通过实际调研，在“合片抽真空”过程中，通常高压釜的压力参数长时间保持不变，对玻璃合片的性能影响较小。而由于温度为非线性、大延迟的动态稳定过程，所以温度对玻璃合片的性能影响则较为显著。如果温度过低，则会造成复合玻璃的起泡、开胶、抽真空效果不理想等；如果温度过高则易使胶片老化，影响合片效果。

本文所研究的远红外线高压釜的温度控制系统，目前是由传感器、控制器、继电器和远红外线加热管组成的。具体控制过程为：传感器采集温度信号，送入控制器；当温度低于设定值时，控制器发出指令，继电器吸合，使红外线加热器接电导通，对胶片进行加热；当温度达到预设值后，控制器向继电器发出断开指令，继电器断开，停止加热。这种断开闭合过程循环往复，形成一种温度的动态平衡，从而保持釜内温度稳定在设定值附近。

由于温度的大延迟、非线性的特点，目前这种以继电器控制加热器的控制方式在恒温阶段的效果不理想，使得釜内温度在恒温阶段会伴有超调、震荡等现象，会使复合玻璃的废品率提高。

目前应用的控制方式，控制效果不理想，控制方式简单，归根结底是没有建立可以作为理论依据的相对精确的数学模型，因此不能通过更为有效的控制方法对温度进行控制。本文对高压釜釜内温度进行温度建模，然后再设计一种控制方式，与温度数学模型相结合后，达到对温度精确控制的目的。

1 高压釜理论模型与建模

1.1 高压釜温度模型机理分析

本文所研究的加热系统主要有多组远红外线加热器组成，对于不同的温度阶段，开启不同组数的远红外线加热器。相比于高压釜采取导热油的加热方式，应用远红外线加热方式具有能量传递迅速的优点。远红外线加热方式，其能量传递的过程首先是电能转化为远红外线的辐射能，然后辐射能转化为热能对胶片进行加热。由于釜内所发生的变化仅仅是胶片吸热蒸发水分并使胶片变软的过程，所以不存在化学反应，即不存在明显的放热过程，由于釜内有大功率风机，可以使釜内空气形成环流，又由于釜内容积相对较小，风机相对较大，因此可以将釜内各处温度视为均匀分布。

设整个系统的能量为W，其中一部分被胶片吸收，使得胶片软化，设其吸收的热量为W吸；另一部分热量为高压釜冷却水带走的热量，玻璃吸收的热量以及釜体散发的热量，并设这部分热量为W散。根据能量守恒定律有：

W=W吸+W散

(1)

由热力学定律可知：

(2)

其中:C表示胶的比热容；T表示高压釜设定温度；k表示高压釜内热量损耗系数；W代表高压釜远红外线加热器输出热量。

对上式等号左边与右边同时求拉普拉斯变化，得：

CsT(s)+kT(s)=W(s)

(3)

移项可得：

(4)

通过对合胶过程高压釜内物理机理的分析，可以得出如式(4)所示类型的温度模型。但由于传热过程涉及热辐射、热对流等热力学过程，热传递是一个较为复杂的过程，通过机理分析以及生活经验得知热传递中存在着较大的时间延迟，即控制效果的滞后性，因此考虑其传递函数时，应该考虑纯时滞过程。

所以，高压釜内的温度模型应该表示为：

(5)

如式(5)所示，通过机理建模，得到了高压釜内的温度模型，是一个一节惯性加延迟的环节。

1.2 高压釜温度建模

通过机理建模，得到式(5)的高压釜模型，为了求模型的未知参数，我们再应用实验建模方式进行未知参数的确定。工程上最常用的是飞升曲线法，即阶跃响应建模法。

其方法为，在对象的输入端加入一个合适的阶跃信号，由信号采集器采集阶跃信号发生以后系统的输出响应，根据阶跃信号发生后对应响应值与时间的关系，计算各个参数。采用飞升曲线测量方法，测出高压釜温度模型的飞升曲线，即可得到控制对象的数学模型。

图1为高压釜在工作状态下的飞升曲线(阶跃电压为380V，且所有加远红外线加热器工作)。

图1 飞升曲线

在获得飞升曲线后，采用Cohn-Coon公式求对象参数[6]。

Conh-Coon公式如下：

(6)

T=1.5(t0.632-t0.28)

(7)

(8)

式中,K为对象的放大系数；T为对象的时间常数；τ为对象的纯滞后常数；t0.28为对象的飞升曲线为0.28y时的时间；t0.632为对象的飞升曲线为0.632y时的时间。

在初始状态，炉内温度稳定在y(0)=30 ℃，然后通以380V的电压，经过3768秒后系统再次达到稳定，此时y(∞)=80 ℃，从记录的数据中，得出t0.632=1 547s，t0.28=788 s。

由公式(6)(7)(8)得出模型参数分别为：K=0.13,T=1 139,τ=409。所以高压釜的温度模型近似为：

(9)

2 控制方法

2.1PID参数整定

通过对高压釜温度控制方式、玻璃合胶过程的特点研究，首先确定PID控制方案是可以应用到玻璃合片的生产过程之中的，PID控制是最典型的控制方法，它结构简单、可靠性强，容易实现，并且可以消除稳态误差，在大多数情况下能够满足性能要求[7]。

在PID控制中，最为关键便是P、I、D三个参数设定。PID参数整定的方法在这里我们应用的是Ziegler-Nichols(齐格勒-尼柯尔斯)参数整定法。

它是在实验阶跃响应的基础上，根据临界稳定性中的Kp值建立起来的。当被控对象的传递函数可以近似为带延迟的一节系统时，齐格勒-尼柯尔斯给出了表1中公式确定Kp、Td、Ti的值的方法。

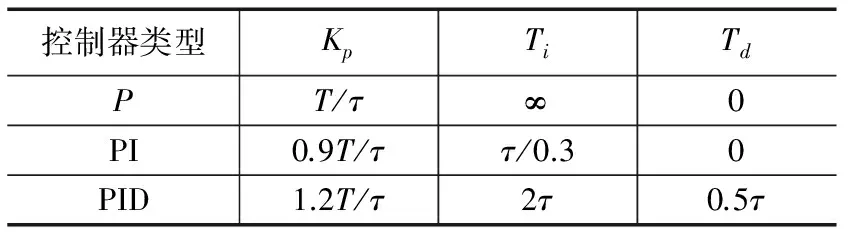
表1 参数表

用齐格勒-尼柯尔斯法则调整PID控制器，给出下列公式：

(10)

由传递函数(9)得：

K=0.13,T=1 139,τ=409

则得到PID参数为：

Kp=3.34,Ki=0.004,Kd=683

2.2 模型参考自适应控制

2.2.1 模型参考自适应控制原理

对高压釜温度模型的建模，是通过绘制飞升曲线，应用“Cohn-Coon公式”进行未知参数的求解，而PID参数整定又是通过温度模型进行求解的，在这个过程中，不可避免的产生了误差，而且单独使用PID控制器，在PID参数确定后并不能在线调整，这样就有可能对最终的控制效果产生一定的影响。因此，本文结合模型参考自适应控制，对PID控制进行辅助控制，从而达到提高PID控制适应性与精度目的。

在自适应控制系统中，模型参考自适应控制系统是其中一类重要的控制系统。其典型结构图如图2所示。在图中，参考模型是自适应机构的辅助系统，它的输出用于表示在该种输入条件下，理想的系统输出是何种类型。可调系统就是被控对象与控制器，它与参考模型在同一个输入信号的作用下同时输出，可调系统输出实际信号，参考模型输出参考信号，它们之间的误差构成了广义误差信号，而自适应机构根据事先设定好的某一准则与广义误差信号，调整可调系统中控制器的参数或施加一个辅助控制信号，以使广义误差趋向于零或使其某个泛函趋向于极小值。这样自适应机构通过参考模型与自适应准则，使得可调系统的输出特性逐渐逼近参考模型的输出特性。

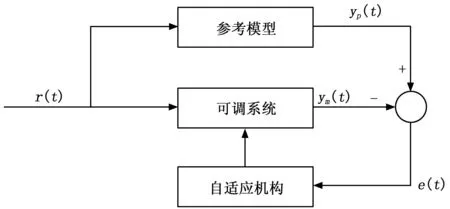
图2 模型参考自适应控制典型结构图

对于本文所研究的温度控制系统，参考模型即所求得的温度模型理想化后的传递函数，可调系统是由PID控制与控制对象组成。

对于模型参考自适应控制来说，其控制的关键是自适应机构的设计，根据被控对象的要求，计算升温过程中的PID参数，通过某一准则不断调整PID参数，使得实际输出不断逼近参考模型输出。

2.2.2 自适应控制律设计方法

自适应律的设计方法[8]有：局部最优化设计方法(MIT律)，用Lyapunov稳定理论设计方法和基于超稳定理论的设计方法。

基于局部参数最优化方法设计是早期提出的一种自适应控制系统的设计方法。它常用的优化方法有牛顿法、梯度法、共轭梯度法等，这些方法易于实现，但是其缺点是没有考虑自适应控制系统的稳定性等问题。因此MIT律在实际的控制系统中很少应用，但它的设计思路还有一定的借鉴作用。

用Lyapunov稳定理论设计方法，针对基于局部参数最优化理论设计的缺陷，人们提出Lyapunov稳定性理论来设计自适应控制系统，这种方法不但可以保证系统的全局渐进稳定性，而且可适用于系统参数大范围变化的情形。

但是基于Lyapunov稳定性理论设计自适应系统，其自适应控制律与所选取的V函数有关[9]，不同的V函数将导致不同的自适应律，这些自适应律的优劣，主要取决于设计者的经验和技巧。

所以基于超稳定性理论的自适应系统设计较好地解决了自适应律的设计问题，自适应系统的参数调整较快。这种设计方式具有一套比较规范的做法，可得到一族自适应系统的设计方案，器设计过程易于被掌握。

2.2.3 自适应律设计

模型参考自适应控制由参考模型、可调系统及自适应机构组成，其结构如图2所示。

考虑系统：

(11)

式中：s=d/dt为微分算子；yp为系统输出；n,m为模型的相对阶次；a,b为模型的系数。

取参考模型为：

(12)

式中,Gm(s)为稳定的HURWITZ多项式；ym为参考模型的输出；g,d为参考模型的系数；l,q为参考模型的相对阶次。

由系统及参考模型得到广义误差信号:

e(t)=ym(t)-yp(t)

(13)

引入自适应误差信号:

δ(t)=-Gm(s)e(t)

(14)

则控制律取为[10]:

(15)

式中,K(t),Ki(t)(i=0,1,...,l)为可调参数。

式中,γ,α为自适应增益系数。

本发明中，控制器采用PID控制器，则可调系统模型为:

(16)

设误差自适应信号δ(t)依旧采用PID控制器的结构形式，根据式(15)分别可得到模型参考自适应PID控制器的控制策略：

(17)

式中,Kp*,Ki*,Kd*为可调PID参数的初值；系数γ>0，α1>0，α2>0，α3>0。

由式(17)解得:

(18)

将(18)带入(16)中，就构成了自适应控制机构。

在本发明中，参考模型为已求得的温度模型式(9)的优化形式。

则由(9)可得参考模型为:

(19)

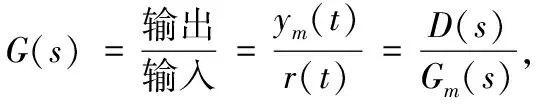
本控制系统的结构图如图3所示。

图3 控制结构图

3 仿真试验与分析

由2.1节得到PID的参数为:

Kp=3.34,Ki=0.004,Kd=683

PID仿真图如图4所示。

图4 PID控制仿真图

仿真结果如图5所示。

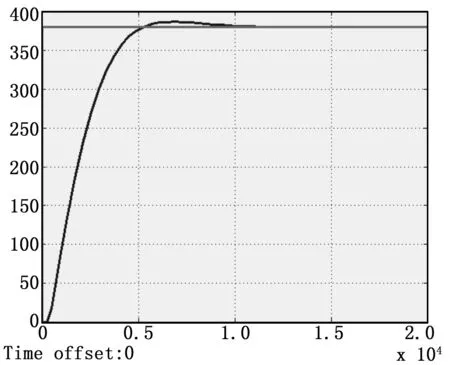
图5 PID仿真曲线

由图5可知，达到峰值的时间为650s，进入稳态时间约为1 000s，超调量为7 ℃。

由2.2.3节可知自适应律设计规则，采用如图6的仿真图。

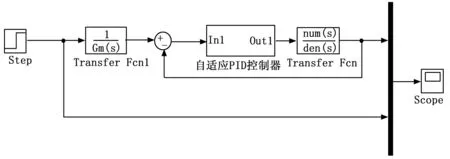
图6 模型参考自适应PID控制仿真图

其中自适应PID控制器结构如图7所示。

图7 自适应PID控制器内部结构

模型参考自适应PID的Simulink仿真曲线如图8所示。

图8 模型参考自适应PID控制仿真曲线

由图8可知，达到峰值的时间为360s，进入稳态时间约为700s，超调量为2.5 ℃。

由实验结果分析得，采用模型参考自适应PID控制的控制效果，达到峰值所需的时间为只采用PID控制所需时间的55.38%，计入稳态所需的时间是只采用PID控制所需时间的70%，超调量约减少了64%。采用模型参考自适应PID控制的控制效果明显优于只采用PID控制的控制效果，其响应速度、响应时间、超调量都明显得到了优化，模型参考自适应PID控制器能够明显改善控制效果，达到理想的控制要求。

4 结论

本文针对复合玻璃“合片抽真空”过程，高压釜温度建模进行了机理分析，通过分析，得出了高压釜温度模型，并利用实测数据绘制成飞升曲线，用两点法求解出了温度模型各个参数的值，给出了高压釜温度模型的数学表达式。

利用数学表达式，运用参数整定公式，得出了PID参数，应用模型参考自适应控制控制与PID控制相结合的控制方式，替换了原来玻璃“合片抽真空”过程中高压釜温度简单的闭环控制方式。运用matlab的simulink仿真，对各项参数进行了调整，而且对PID控制与模型参考自适应PID控制的控制效果进行了对比，从仿真结果可以看出，基于模型参考自适应的PID控制应用于复合玻璃合片抽真空过程，比原本的简单闭环控制与常规的PID控制具有更快的调节速度，调节精度更高，提高了温度控制系统的动态品质和稳态精度。

[1] 李 超,高 鹏.玻璃复合及组件技术[M].北京：化学工业出版社，2014.

[2] 唐 辉,张晓春,方瑞萍.夹层玻璃的制造工艺及其生产和能源效率[J].玻璃与搪瓷,2014,42(3):33-38.

[3] 刘志海.夹层玻璃的发展现状及趋势[J].中国建材，2003,9:64-66.

[4] 首诺公司.PVB在高级夹层玻璃中的有效加工[J].上海建材，2011,3:30-32.

[5] 孟兴蛟.夹层玻璃关键生产工艺探讨[J].建材发展导向，2015,13(4):42-45GB/T16159-1996.

[6] 孙 健.基于神经单元PID的电阻炉智能温度控制系统[D].大连:大连理工大学，2008.

[7] 陶永华.新型PID控制及其应用[M].北京：机械工业出版社，2002.

[8] 刘小河,管 萍,刘丽华.自适应控制理论级应用[M]. 北京：科学出版社，2011.

[9] 刘小河.非线性系统分析与控制引论[M].北京：国防工业出版社，1995.

[10] Andrievsky B,Fradkov A.Implicit model reference adaptive controller based on feedback Kalman-Yakubovich lemma[A].The Proceedings of the IEEE Conference on Control Applications[C].Scotland UK,1994.1171-1174.

Temperature Control of Autoclave Based on Model Reference Adaptive System and PID Control

Wang Yuhua, Zheng Xiaojian

(China Jiliang University, Hangzhou 310018, China)

Based on investigation of glass laminating and vacuumizing, it shows that the temperature control method which is in use is too simple to get a better result. This method causes overshoot, shock and so on. So design a more accurate method called temperature control of autoclave based on model reference adaptive system and PID control to deal with those problems above. Frist, it will model the temperature of autoclave with the experimental datas. And then set the parameters of PID control by the temperature models. Next the parameters can be adjusted on line based on the model reference adaptive system(MRAS). That makes up deficiency of classical PID control and use the advantages of PID. From the simulation, it shows that the method can reduce the overshoot and improve dynamical property.

mathematical modeling; PID control; MRAS; parameters self-adjustment

2016-11-29；

2016-12-23。

王玉华(1964-)，女，吉林通化人，教授，硕士研究生导师，主要从事开关电源、控制方向的研究。

1671-4598(2017)05-0105-04DOI：10.16526/j.cnki.11-4762/tp

TP

A