基于帕累托纳什均衡博弈的电网/多元家庭用户互动多目标优化算法

王德志，张孝顺，余 涛，刘前进，潘振宁

（华南理工大学 电力学院，广东 广州 510641）

0 引言

近年来，随着分布式电源和电动汽车的大量普及和发展，国内外较多学者已展开对主动配电网技术各方面的研究［1-3］，不少单位也开始开展相应的示范工程应用［4］。主动配电网技术通过采取科学的措施，引导用户进行有效用电，优化资源配置，实现电力服务成本最小的智能用电管理［5］。其中，如何对主动配电网下的多元家庭用户进行高效的互动便是一个值得探讨的问题。

在需求侧用户中，家庭用户户数占比最大，不同用户用电习惯差异性也较大，因此，多元家庭用户存在较大的互动调度优化潜力。对于主动配电网调度中心而言，调度人员可以通过与多元家庭用户的能量管理系统进行互动，利用最优调度和智能控制方法来达到节能、减少碳排放的目的，从而满足用户满意度和主动配电网需求响应要求。家庭能量管理系统 HEMS（Home Energy Management System）是以智能电网和智能家居为基础，依托于电网和家庭之间的通信，结合分时电价或实时电价、天气条件、需求响应等，将家庭中的分布式电源、用电设备、储能设备等有机结合在一起的智能控制系统。因此，HEMS是电网与多元家庭用户互动的纽带，电网侧根据需求及某种激励手段制定家庭用电计划，并发布给HEMS，用户即可选择是否接纳该用电计划并实施。

在制定能量管理策略方面，文献［6］提出一种基于功率预测与反馈的能量管理策略来平抑储能波动。文献［7］将用户侧负荷按其特性与运行特征进行了分类考虑来分别进行优化。文献［8］考虑了用户需求及家庭用户的多元特性，针对不同的优化目标搭建了最优调度模型。文献［9］提出了综合考虑新能源、蓄电池、电动汽车和能量优化的HEMS，阐述了HEMS的当前现状及未来趋势，但缺少深入的理论研究，不能直接指导HEMS模型的具体搭建。在满足必须运行且不参与调度的电器、新能源发电及电网需求响应要求前提下，文献［10］提出了基于动态电价的家庭用电管理模型，但其优化模型只追求用户电费达到最低，而忽略了用户的实际用电舒适度。为此，文献［11］将用户舒适度转化为用电成本，引入了一种有效的电池充放电管理策略。此外，文献［12］还详细给出了室温、水温调节模型以及不同类型用电设备的处理方法。文献［13］在处理目标函数时，通过将用户的用电行为量化为利益指标，综合考虑了用户电费及用户用电满意度的优化目标。

目前，对于HEMS的研究大多数是针对单个家庭用户优化，而缺少电网侧与多元家庭用户的互动多目标优化。与单个家庭用户优化相比，多元家庭用户优化具有负荷总量大、家庭设备多样、用电习惯不同等特点，可调度的空间会更大，然而随着用户数量的增加，优化变量将剧增，从而导致“维数灾”，因此对优化算法的搜索性能要求更高。多元用户的相互作用主要体现在其参与电网负荷曲线优化上，电网通过采集不同用户的用电、需求等信息，从而制定出多元用户协同出力的用电计划，这与单用户优化的区别在于，单用户总体用电量少，对于电网影响较小，而多元用户所拥有的发/用电设备更多，其对于整个配电网的影响较大，因此通过多元用户间的相互协同作用能够实现电网侧优化负荷曲线的目标。随着电力市场的迅速发展，受发/用电收益的驱使，用户与电网互动的主动性和积极性将随之增加，这也利于电网的安全经济运行，因此，“电网/用户互动”将是未来电力市场的发展方向之一。同时，主动配电网的快速发展促使更多的分布式电源及电动汽车接入家庭，增加了HEMS的复杂性。为此，基于单个家庭用户模型，本文搭建了主动配电网下的电网/多元家庭用户互动多目标优化模型。首先，对用电设备相似的家庭用户进行分类，以减少优化变量个数，避免“维数灾”。然后，提出了基于帕累托（Pareto）纳什（Nash）均衡博弈的非支配邻域免疫 NNIA（Nondominated Neighbor Immune Algorithm）［14］多目标优化算法对其进行求解。仿真算例还引入了其他2种常用的多目标优化算法进行对比分析，以验证本文所提算法的有效性。

1 多元家庭用户分类及系统模型

1.1 多元家庭用户分类

本文所提的多元家庭用户是指拥有不同发/用电设备、不同用电习惯的家庭用户群。首先将多元家庭用户划分为不同类型，其划分标准主要是考虑光伏、电动汽车以及家庭可控用电设备等的不同。为了方便进行统一管理，降低优化变量个数，多元用户家庭可划分为以下3类。

a.Ⅰ类家庭：有光伏有电动汽车储能。

b.Ⅱ类家庭：无光伏有电动汽车储能。

c.Ⅲ类家庭：无光伏无电动汽车储能。

在单个家庭中，家庭设备分为可控系统及不可控系统两大部分，其中家庭可控系统主要包括储能系统、室温调节系统、水温调节系统及光伏发电系统，不可控系统主要包括家庭基本负荷，如照明、冰箱、厨房电器等。本文电网/多元家庭用户互动框架如图1所示。

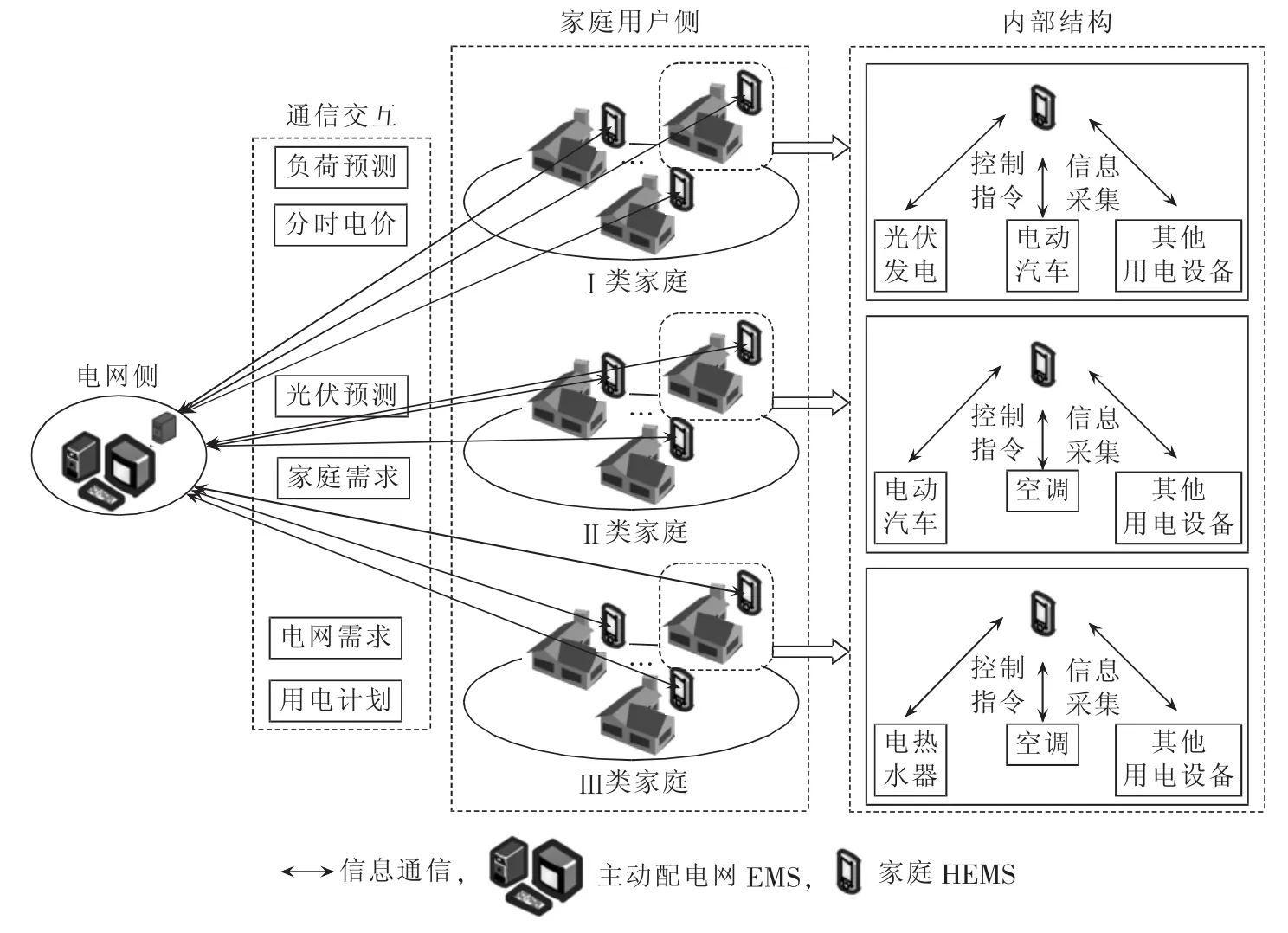
图1 电网/多元家庭用户互动框架Fig.1 Frame of interaction between power grid and multi-home user

1.2 系统模型

在多元家庭用户框架中，不同组件之间通过互相配合来达到互动的目的。而不同类型的家庭比例会影响优化效果，尤其是储能系统比例的减少会降低对负荷的移峰填谷作用。而家庭中的光伏及储能设备则会影响家庭的用电量、电费支出等。对于光伏发电系统，受时间、天气等限制，每日出力不一致，对于一个家庭，不仅控制难度大，并且如果直接接入家庭使用或者直接并网发电，会造成消纳不足和电网不稳定等问题。通过与储能系统的配合，使得用户可以利用蓄电池来进行光伏电能的转移，从而实现光伏发电的自发自用，将经济利益最大化［15］。光伏电源的输出功率与太阳辐照度和温度有关，通过日前对辐照度曲线和温度等信息的预测以及历史发电数据的提炼，即可获得第二天各个家庭用户的光伏出力预测曲线，便于日前的调度优化。家庭当中的可控负荷则通过智能算法求解出能够合理调度使其工作在满足用户生活舒适度需求的最优点。

1.2.1 储能系统模型

电动汽车接入家庭为家庭提供了可调度的储能系统［16］，主要通过对电动汽车的充放电计划进行优化，从而实现光伏消纳及负荷转移。另外本文所提到的电动汽车都属于V2G类型。目前，电动汽车的储能蓄电池主流是锂电池，其充放电过程以恒功率进行［17］。为了简化计算，将充放电分时段进行离散化处理，主要考虑蓄电池充放电过程中的剩余容量。

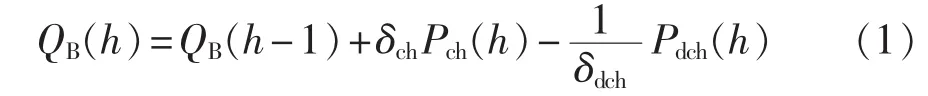
其中，QB（h）为h 时刻蓄电池剩余容量；Pch（h）、Pdch（h）分别为h 时刻充、放电功率；δch、δdch分别为充、放电效率。

此外，蓄电池不在工作状态时会产生静态损耗。

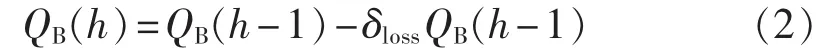
其中，δloss为静态损耗百分比。

本文主要通过对电动汽车的充放电计划进行优化，从而实现光伏消纳及负荷转移。

1.2.2 储能与光伏调度模型

以I类家庭为例，蓄电池及光伏电源的调度操作［18］如下。

（1）当前有光伏发电，则电动汽车蓄电池利用光伏发电进行充电：

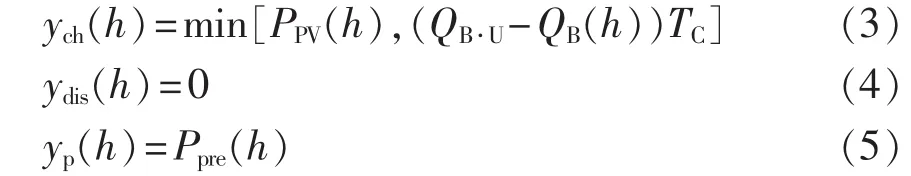
其中，ych（h）为蓄电池优化后的充电功率；PPV（h）为光伏出力；QB·U为蓄电池容量上限；TC为电动汽车蓄电池每小时可充电的最大百分比；ydis（h）为蓄电池优化后的放电功率；yp（h）为用户与电网的交换功率；Ppre（h）为预测负荷。

（2）当前无光伏发电，则有如下情况。

a.当前电价为低电价且电动汽车蓄电池可充电。

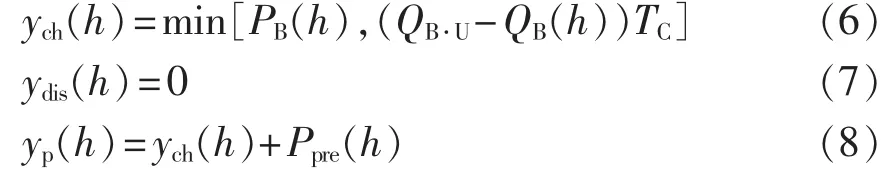
其中，PB（h）为蓄电池优化前的充放电功率。

b.当前电价为高电价、电动汽车蓄电池可放电且预测负荷高于预测日平均负荷值。

其中，QB·L为蓄电池容量下限；TD为电动汽车蓄电池每小时可放电的最大百分比。

c.其他情况。

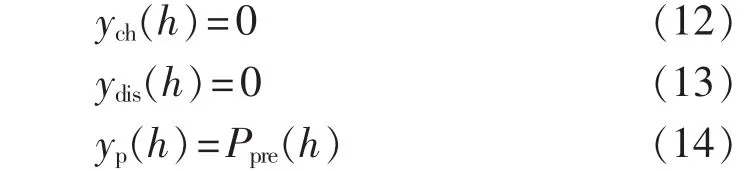
其中，ych（h）为蓄电池充电功率；ydis（h）为蓄电池放电功率；yp（h）为用户与电网的交换功率；TC和 TD分别为电动汽车蓄电池每小时可充放电的最大百分比；Ppre（h）为预测负荷。

对于Ⅱ类家庭，其储能调度模型可参见Ⅰ类家庭的无光伏发电情况。而对于Ⅲ类家庭，既不包含光伏，又不包含储能，因此调度模型可参见Ⅰ类家庭在无光伏发电下的情况c。

1.2.3 室温调节系统模型

室温调节负荷主要为空调，从而主要控制空调功率以调节室温。本文采用分时段离散处理，根据室内外温度及房间参数，由热量平衡原理建立其热力学模型［19-20］。

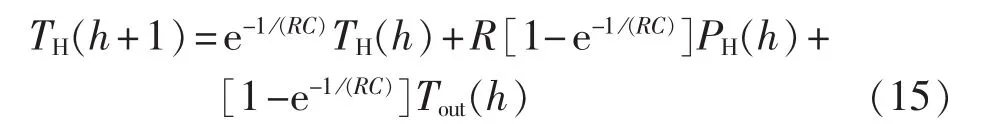
其中，R为房间热阻；C为房间热容量；Tout（h）为h时刻室外温度；PH（h）为h时刻室温调节功率。

1.2.4 水温调节系统模型

水温调节负荷主要为电热水器，控制电热水器的开关调节水温。根据能量守恒原理，水温调节的离散数学模型可描述如下［19］：

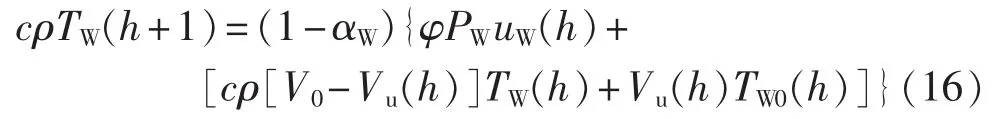
其中，αW为水箱能量散失系数；φ为电能与热能交换系数；V0为水箱体积；Vu（h）为h 时刻用水量；TW0（h）为h时刻自来水温度；PW为热水器加热功率；uW（h）为热水器开关；c和ρ分别为水的比热容和密度。

2 电网/多元家庭用户互动多目标优化模型

2.1 目标函数

2.1.1 家庭侧目标函数

典型的家庭电器中，与人体舒适度相关的主要有空调及热水器，通过改变室温以及水温来调节人体舒适度，虽然湿度等因素对于人体舒适度也有影响，但在普通家庭当中，其影响因子相对较小，故在本文建模仿真当中主要考虑室温与水温。

对于家庭用户，舒适度目标是使实际室温和水温与期望值偏差最小，以家庭的室温和水温与期望值的和方差来表示，同时满足家庭舒适度约束条件：

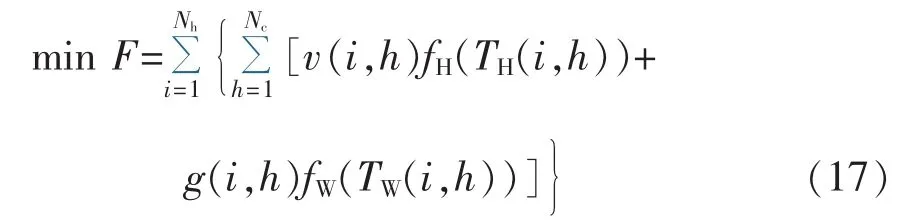
其中，F为舒适度目标函数；Nh为系统家庭个数；Nc为一天的仿真点数；TH（i，h）为h时刻 i家庭室内温度；TW（i，h）为h 时刻 i家庭水温；v（i，h）和 g（i，h）分别为h时刻i家庭室温和水温目标的权重系数；fH和fW分别为室温、水温与其需求值偏差的平方，具体可表示如下：

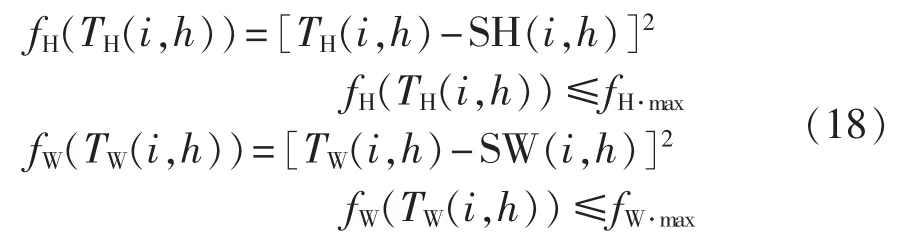
其中，SH（i，h）和 SW（i，h）分别为h 时刻 i家庭室温和水温的期望值；fH·max和fW·max为用户舒适度目标可接受的上限。

为考虑用户舒适度具有一定可适应的变化范围，本文假设室温偏差为±2℃，水温偏差为±5℃，其可表达成如下所示的约束条件。

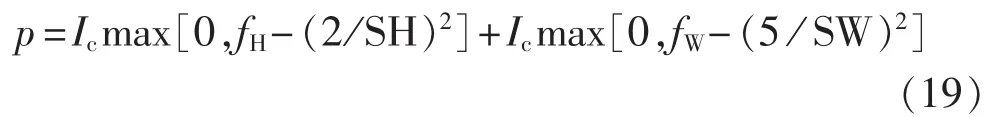
其中，Ic为一个足够大的常数。

2.1.2 电网侧目标函数

对于电网侧，家庭负荷曲线波动程度越小越好，采用负荷曲线标准差最小的负荷曲线优化目标。其中，负荷曲线优化目标是以一天Nc个点的负荷曲线的标准差来评估，具体可表示如下：

其中，σ 为负荷曲线标准差；Pgrid（i，h）为h 时刻 i家庭与电网的交换功率；μ为一天所有家庭负荷的平均值。

2.2 模型约束条件

a.有功功率平衡约束。

电网和家庭间的能量交换须满足能量守恒定律：

其中，PBatt（h）为h 时刻蓄电池的功率；Po（h）为基本负荷；PPV（h）为光伏出力。

b.储能系统约束。

蓄电池约束除了满足最大充、放电功率外，考虑蓄电池寿命，最低使用容量不得低于30%。

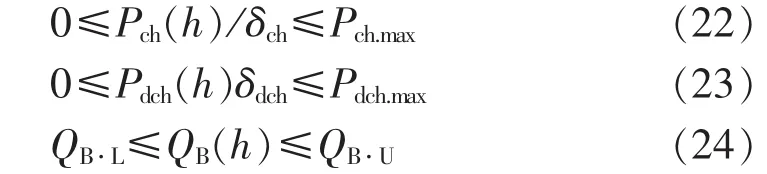
其中，Pch.max和Pdch.max分别为蓄电池充、放电最大功率；QB·U和 QB·L分别为蓄电池容量上、下限。

c.室温调节和水温调节系统约束。

空调出力须满足功率上限，热水器是开关型负荷，且室温及水温加热须满足上限。

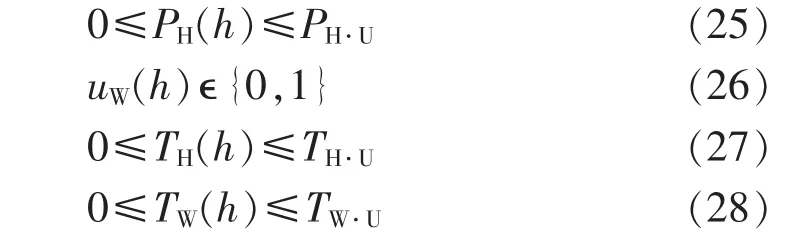
其中，PH·U为室温调节功率上限；TH·U和 TW·U分别为室温和水温上限。

3 电网/多元家庭用户互动多目标优化求解算法

3.1 Pareto优化理论及NNIA

基于Pareto理论的多目标优化问题MOP（Multiobjective Optimization Problem）可用数学描述如下：

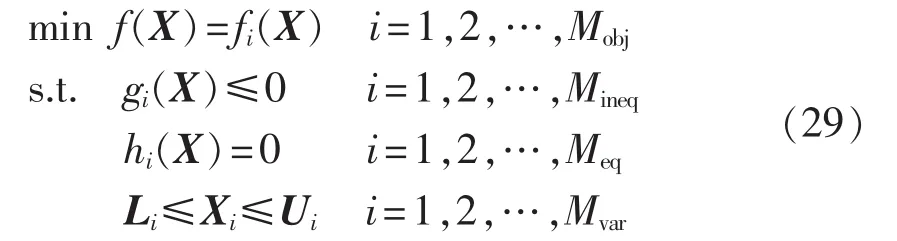
其中，fi为第i个目标函数；X 为决策变量；Mobj、Mineq、Meq、Mvar分别为目标函数、不等式约束、等式约束和决策变量的个数；Ui和Li分别为决策变量的上、下边界。

满足式（29）中所示约束条件的向量称作可行解，即解向量。假设XA、XB是式（29）所示的MOP的2个解向量，当且仅当满足式（30），则称与XB相比，XA是支配XB。对于每个解向量，若不存在一个比该解的各个目标函数值都优的更优解，则称之为非劣解，即Pareto最优解。整个可行空间内的Pareto最优解即为Pareto最优解集，其对应的目标矢量组成的曲面称之为Pareto前沿。

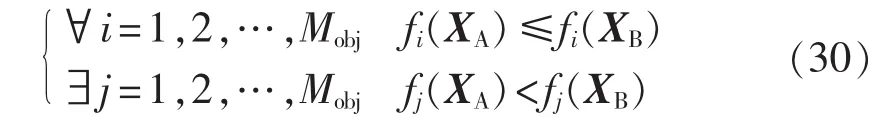
对于本文提出的电网/多元家庭用户互动多目标优化模型，其目标函数主要分为家庭用电舒适度式（17）和负荷曲线优化式（20），其中舒适度目标综合考虑了水温和室温2个指标。此外，本文的等式约束及不等式约束条件可详见式（21）—（28）。

本文采用基于人工免疫系统的多目标优化算法NNIA来求上文所提多目标优化模型。该算法具有寻优效果好、收敛速度快等优点。NNIA受人工免疫系统中多样性抗体共生、少数抗体激活的现象启发，采用基于非支配的邻域个体选择机制，仅选取少数相对孤立的非支配个体作为活性抗体，然后根据这些少数的活性抗体的拥挤程度按一定的比例进行克隆复制，对克隆后的抗体群采用不同于普通遗传算法的重组和变异操作，进而加强对Pareto前沿中比较稀疏部分区域的搜索，从而达到寻求最优非劣解的目的。NNIA流程图如图2所示。

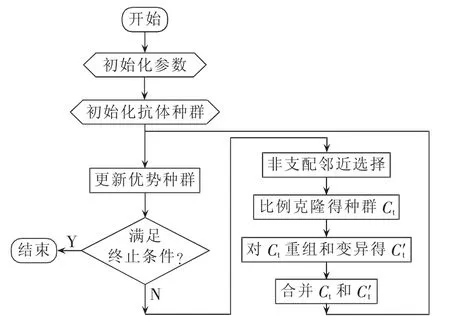
图2 NNIA流程图Fig.2 Flowchart of NNIA

3.2 基于Nash均衡博弈的多目标决策

获得最终Pareto前沿后还需从该组解中选择一个最优折中解作为最终决策。本文的多目标决策问题可转化为一个Nash均衡对策问题，根据非合作博弈论可知，不同个体组成不同层次的联合体，通过共同努力争取从而使得各自联合体利益达到最大化，2个相互冲突的优化目标可认为是非合作决策参与者。因此，本文利用基于Nash均衡点的多目标决策模型［21］对最优折中解进行求解，以获得对应最佳用电策略。该多目标非合作均衡决策模型包含一个求解前沿解集空间中联合概率分布的优化问题［22］，其数学描述如下：

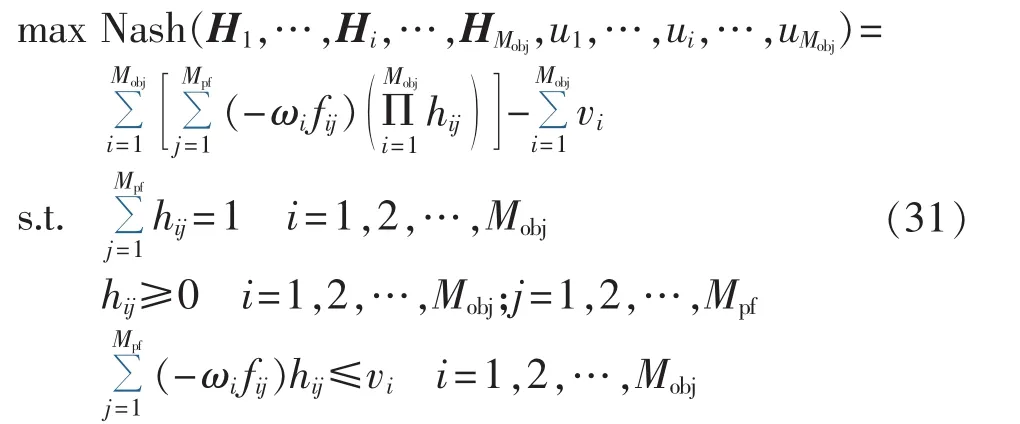
其中，Hi= ［hi1， …，hij，…，hiMpf］为第i个目标的均衡解，代表着Pareto最优解集对该目标上的概率分布；hij为第j个Pareto最优解对应于第i个目标的均衡值；fij为第j个Pareto最优解第i个目标的归一化适应值；ui为第i个目标参与者期望适应值的上限；Mpf为Pareto最优解的个数；Mobj为目标个数；权重系数ωi代表第i个目标函数的相对重要性。优化问题式（31）是一个典型的带约束非线性规划问题，可易于由贯序二次规划求解［23］，从而可为各参与者提供一系列均衡值。而具备如式（32）所示的最佳联合均衡值的Pareto最优解即为最优折中解。

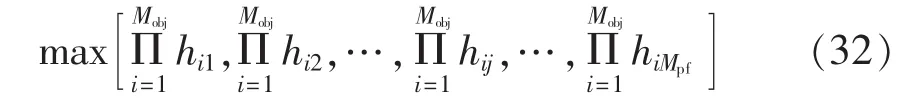
4 仿真算例

4.1 仿真算例配置

本文的多元家庭用户算例规模为100户；家庭采用典型工作日用电行为，并假设每个家庭能完全响应电网需求；优化时间尺度为Δt=1 h，仿真时间为24 h。此外，蓄电池、光伏发电、室温调节及水温调节等参数如表1所示，其他仿真算例数据曲线如图3所示。

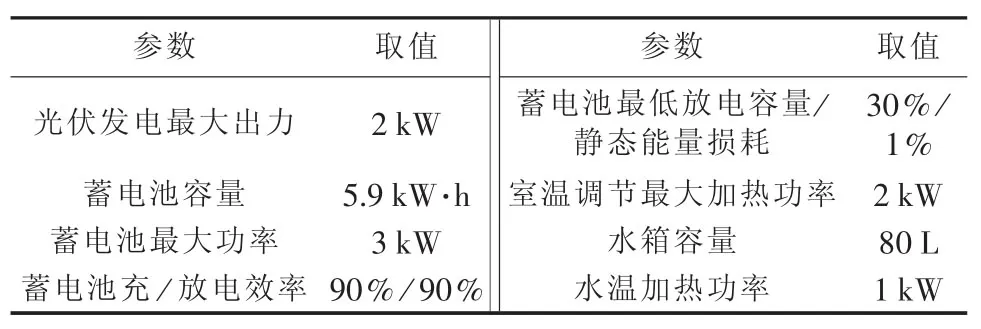
表1 参数设置Table 1 Parameter settings

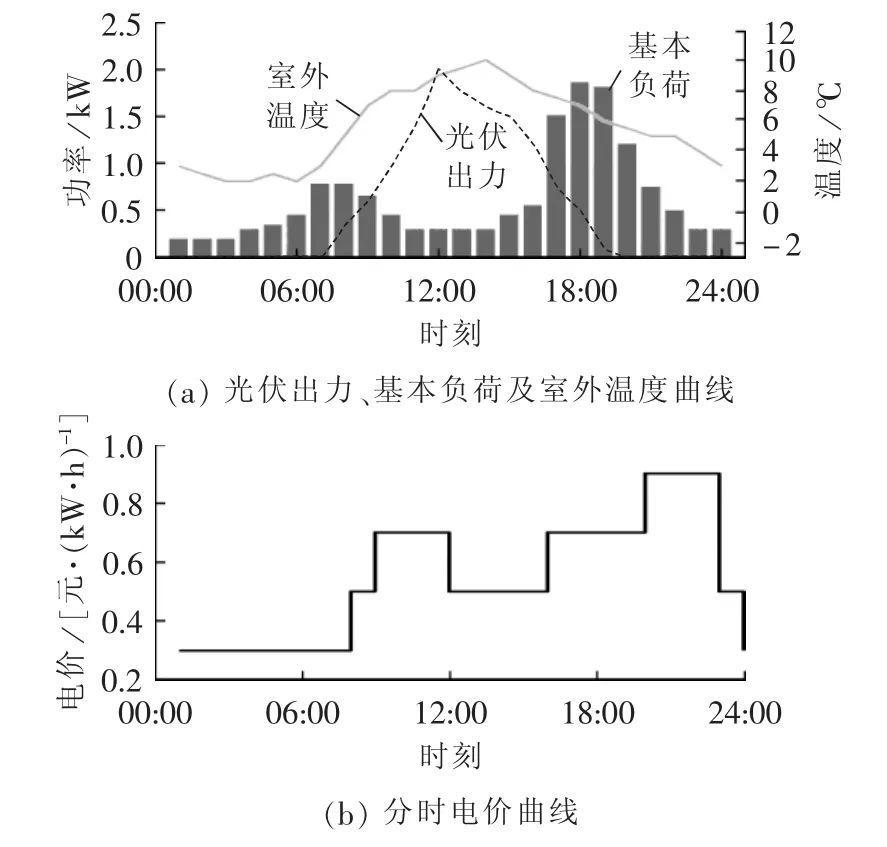
图3 其他仿真算例数据曲线Fig.3 Other data curves for case simulation

4.2 仿真结果比较分析

4.2.1 3类家庭负荷曲线特性仿真分析

取100个家庭用户进行仿真实验，比较各类型家庭对改善负荷曲线的作用，其中Ⅲ类家庭为普通家庭，对负荷曲线无改善效果，可视为基本负荷曲线，仿真结果如图4所示。从图中基本负荷曲线可知，普通家庭的负荷曲线波动较大，在上午和下午的上班时间为用电低谷，而19:00—22:00为用电高峰期。

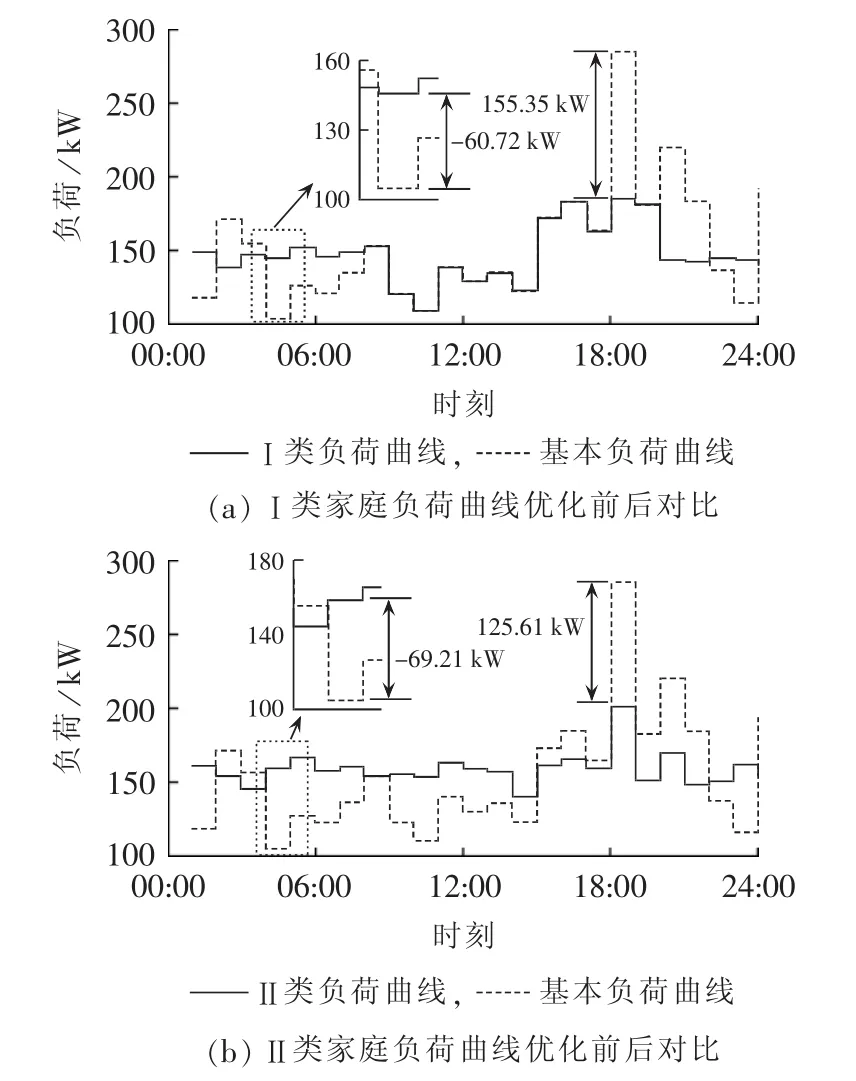
图4 各类家庭负荷曲线仿真结果Fig.4 Simulative household load curve for different home types

当引入蓄电池后，如Ⅱ类家庭，由图4（b）可知，削峰填谷效果及抑制负荷曲线波动效果十分明显，其峰值降低了155.35kW，而谷值相应提高了60.72kW。接入光伏是提高家庭经济性的重要措施，在有光伏发电期间，储能系统优先储存光伏电量并在用电高峰期及高电价时段使用。从图4（a）可以看出，Ⅰ类家庭在光伏发电期间能够有效消纳光伏电量，而在用电高峰期优先使用蓄电池供电，这不仅有助于削峰填谷，且由于蓄电池消纳了更多的光伏电量，减少了电网供电比例，能使用户的电费支出显著降低。

4.2.2 不同类型家庭比例仿真结果分析

为研究不同家庭用户类型比例对仿真结果的影响，本文将100个家庭用户划分成不同类型比例分别进行仿真分析，具体分为3种情况，如表2所示。

表2 不同类型家庭比例设置Table 2 Proportions of different home types

a.Nash均衡决策。

在每种情况下，算法都会求解得到一组最优解集，即Pareto前沿，如前文所述，本文采用Nash均衡博弈决策从中选取出最优折中解作为多元家庭用户互动调度多目标优化的最终决策解，具体可参考图5给出的Case 1下的示例。

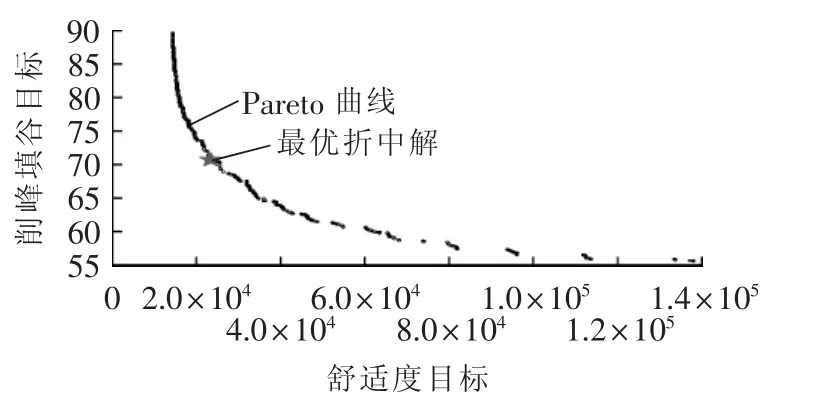
图5 Pateto曲线及最优折中解Fig.5 Pareto curves and optimal compromise solution

b.家庭舒适度仿真结果分析。

从图6—8给出的不同情况下100个家庭室温及水温的盒须图可以看出：在满足式（19）中用户舒适度约束条件下，室温及水温能够基本分布在用户期望附近，并且其偏差范围基本符合式（19）要求。针对不同情况下的结果，仍然可以看出，家庭类型比例的变化对于用户舒适度影响较小，即其室温与水温基本能够满足用户需求，这也进一步说明了本文模型对满足用户舒适性目标的有效性。

c.负荷曲线优化效果仿真结果分析。

图9是3种情况在优化前后的负荷曲线对比图，从图中可以明显看出，3种情况对于抑制负荷曲线波动及削峰填谷均发挥了作用，而Case 1和Case 2因储能设备更多，对于负荷转移发挥了更大的作用。表3中列出了优化前后3种情况的负荷曲线标准差（σ）、峰谷差率（ΔPp-p）以及节省电费的对比数据。从表3中3种情况相关的仿真结果可以看出，经过优化，3种情况下100个家庭的负荷曲线标准差平均降低了59.3661 kW，并且峰谷差率平均减少了21.17%。在经济目标上，3种情况下用户平均节省电费88.65元。由此可以看出本文所提模型在优化负荷曲线以及帮助用户提高经济性方面具有良好的效果。

表3还列出了3种不同算法的仿真结果比较，从表中数据可以看出，NNIA在3种参数中具有一定的优势，而SPEA-Ⅱ也有着较良好的表现，但从仿真过程中看，NNIA在收敛速度上明显优于另外2种算法，而SPEA-Ⅱ对于用户舒适度效果较差且收敛速度慢；而从数据中明显可以看出NSGA-Ⅱ远不如其他2种算法的表现。由此可以看出本文所提算法具有明显的优势。

图6 Case 1家庭室温及水温盒须图Fig.6 Box-and-whisker plots of water temperature and room temperature for Case 1

图7 Case 2家庭室温及水温盒须图Fig.7 Box-and-whisker plots of water temperature and room temperature for Case 2

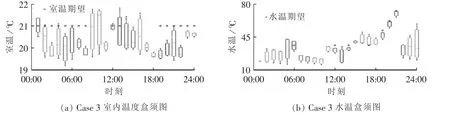
图8 Case 3家庭室温及水温盒须图Fig.8 Box-and-whisker plots of water temperature and room temperature for Case 3

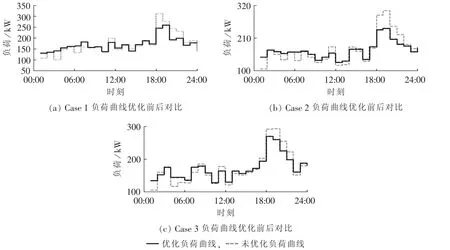
图9 不同家庭类型家庭负荷曲线仿真结果Fig.9 Simulative household load curve for different cases

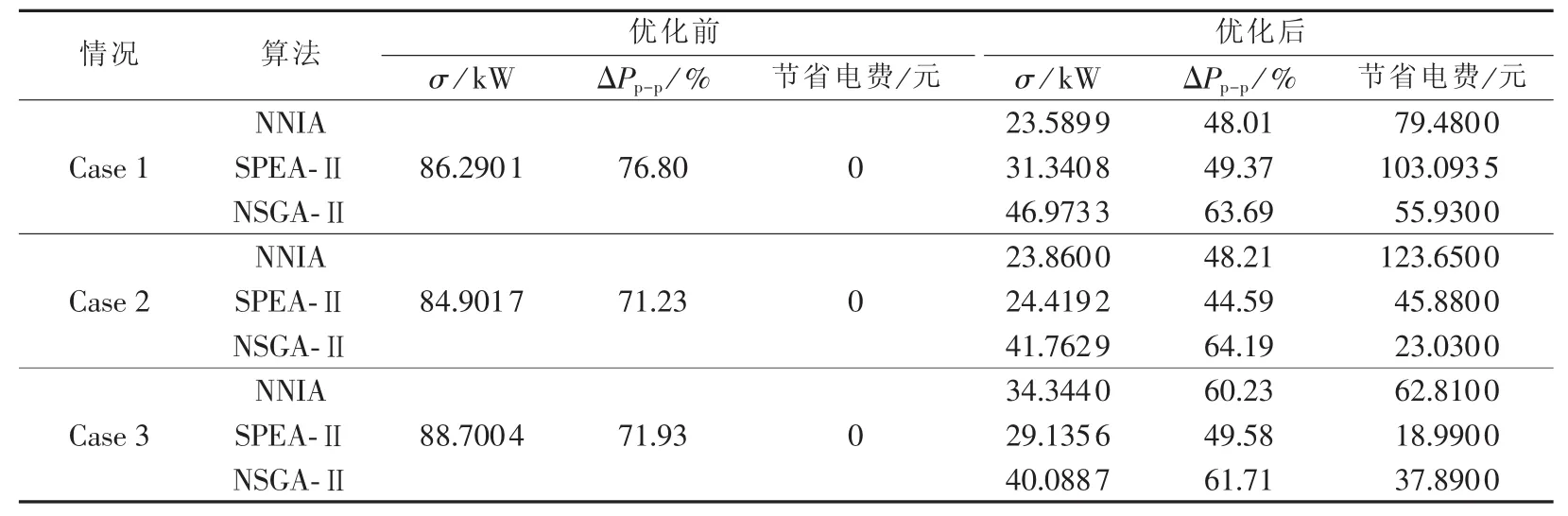
表3 各家庭类型仿真结果Table 3 Simulative data for different cases

5 结论

本文提出的基于Pareto Nash均衡博弈的电网/多元家庭用户互动多目标优化算法，通过家庭与电网的互动，实现利用光伏发电、电动汽车接入和家庭负荷协同调度来满足用户用电舒适度、经济性以及优化电网侧负荷曲线。采用了NNIA来求解Pareto前沿，并利用Nash均衡博弈决策求取最优折中解。相比于只考虑单用户家庭经济性或家庭舒适性的优化，本文所提模型在满足用户用电舒适度的同时，增加光伏发电的自发自用，并引入电动汽车作为家庭储能设备，从而解决电网侧负荷曲线优化以及用户的经济性。通过仿真算例表明，本文所建立电网/多元家庭用户互动多目标优化算法能够满足用户舒适度以及经济性，也同时能够满足电网侧负荷曲线优化问题。

目前，本文尚未涉及对电网侧分时电价的制定策略及用户的用电费用进行优化，因此，笔者在今后研究工作中将引入多个维度的互动博弈，求解出电网侧电价和用户侧用电计划的最优Nash均衡点。

参考文献：

［1］SAMUELSSON O，REPO S，JESSLER R，et al.Active distribution network-demonstration project ADINE ［C］∥Proceedings of the 2010 IEEE PES Innovative Smart Grid Technologies Conference Europe.2010.Gothenburg，Sweden：［s.n.］，2010：1-8.

［2］尤毅，刘东，于文鹏，等.主动配电网技术及其进展［J］.电力系统自动化，2012，36（18）：10-16.YOU Yi，LIU Dong，YU Wenpeng，etal.Technologyand its trends of active distribution network［J］.Automation of Electric Power Systems，2012，36（18）：10-16.

［3］赵波，王财胜，周金辉，等.主动配电网现状与未来发展［J］.电力系统自动化，2014，38（18）：125-135.ZHAO Bo，WANG Caisheng，ZHOU Jinhui，et al.Present and future development trend of active distribution network［J］.Automation of Electric Power Systems，2014，38（18）：125-135.

［4］刘东，陈云辉，黄玉辉，等.主动配电网的分层能量管理与协调控制［J］.中国电机工程学报，2014，34（31）：5500-5506.LIU Dong，CHEN Yunhui，HUANG Yuhui，etal.Hierarchical energy management and coordinary control of active distribution network［J］.Proceedings of the CSEE，2014，34（31）：5500-5506.

［5］王伟，何光宇，万钧力，等.用户侧能量管理系统初探［J］.电力系统自动化，2012，36（3）：10-15.WANG Wei，HE Guangyu，WAN Junli，et al.Preliminary investigation on user energy management system［J］.Automation of Electric Power Systems，2012，36（3）：10-15.

［6］田军，刘征宇，舒军，等.适用于工业园区的微电网系统能量管理［J］.电力自动化设备，2016，36（11）：45-50.TIAN Jun，LIU Zhengyu，SHU Jun，et al.Energy management for micrigrid system of industrial park［J］.Electric Power Automation Equipment，2016，36（11）：45-50.

［7］童小娇，尹昆，刘亚娟，等.包含可控负荷的微电网经济调度［J］.电力自动化设备，2015，35（10）：21-28.TONG Xiaojiao，YIN Kun，LIU Yajuan，et al.Economic dispatch for microgrid with controllable loads［J］.Electric Power Automation Equipment，2015，35（10）：21-28.

［8］刘经浩，贺蓉，李仁发，等.一种基于实时电价的HEMS家电最优调度方法［J］.计算机应用研究，2015，32（1）：132-137.LIU Jinghao，HE Rong，LI Renfa，et al.Optimal scheduling model for home energy management system based on real-time electricity pricing［J］.Application Research of Computers，2015，32（1）：132-137.

［9］项胜，何怡刚，王金平.家庭智能用电系统的实现方法［J］.电力科学与技术学报，2014，29（3）：40-44.XIANG Sheng，HE Yigang，WANG Jinping.The implementation of domestic intelligent energy system［J］.Journal of Electric Power Science and Technology，2014，29（3）：40-44.

［10］KUMARAGURUPARAN N，SIVARAMAKRISHNAN H，SAPATNEKAR S S.Residential task scheduling under dynamic pricing using the multiple knapsack method［C］∥Proceedings of the 2012 IEEE PES Innovative Smart Grid Technologies Conference Europe.2012.Gothenburg，Sweden：［s.n.］，2012：1-6.

［11］IWAFUNE Y，IKEGAMI T，FONSECA J G D S，et al.Cooperative home energy management using batteries for a photovoltaic system considering the diversity of households［J］.Energy Conversion&Management，2015，96：322-329.

［12］HUANG Y，TIAN H，WANG L.Demand response for home energy management system［J］.International Journal of Electrical Power&Energy Systems，2015，73：448-455.

［13］PEDRASA M A A，SPOONER T D，MACGILL I F.Coordinated scheduling of residential distributed energy resources to optimize smart home energy services［J］.IEEE Transactions on Smart Grid，2010，1（2）：134-143.

［14］GONG M，JIAO L，DU H，et al.Multiobjective immune algorithm with nondominated neighbor-based selection［J］.Evolutionary Computation，2008，16（2）：225-55.

［15］王守相，孙智卿，刘喆.面向智能用电的家庭能量协同调度策略［J］.电力系统自动化，2015，39（17）：108-113.WANG Shouxiang，SUN Zhiqing，LIU Zhe.Co-scheduling strategy of home energy for smart power utilization［J］.Automation of Electric Power Systems，2015，39（17）：108-113.

［16］YOKOYAMA R，YOSHIMI K，KONDOU H，et al.Contribution of electric vehicles for energy management in smart houses with uncertain power generation［J］.Automation of Electric Power Systems，2011，35（22）：18-24.

［17］王锡凡，邵成成，王秀丽，等.电动汽车充电负荷与调度控制策略综述［J］.中国电机工程学报，2013，33（1）：1-10.WANG Xifan，SHAO Chengcheng，WANG Xiuli，et al.Survey of electric vehicle charging load and dispatch control strategies［J］.Proceedings of the CSEE，2013，33（1）：1-10.

［18］石庆均，江全元.包含蓄电池储能的微网实时能量优化调度［J］.电力自动化设备，2013，33（5）：76-82.SHI Qingjun，JIANG Quanyuan.Real-time optimal energy dispatch for microgrid with battery storage［J］.Electric Power Automation Equipment，2013，33（5）：76-82.

［19］SHAO S，PIPATTANASOMPORN M，RAHMAN S.Development ofphysical-based demand response-enabled residentialload models［J］.IEEE Transactions on Power Systems，2013，28（2）：607-614.

［20］DONLAN P S，NEHRIR M H，GEREZ V.Development of a Monte Carlo based aggregate model for residential electric water heater loads［J］.Electric Power Systems Research，1996，36（1）：29-35.

［21］谢政.对策论导论［M］.北京：科学出版社，2010：168-189.

［22］周斌，宋艳，李金茗，等.基于多群组均衡协同搜索的多目标优化发电调度［J］.电工技术学报，2015，30（22）：181-189.ZHOU Bin，SONG Yan，LI Jinming，et al.Multiobjective optimal generation dispatch using equilibria-based multi-group synergistic searching algorithm［J］.Transactions of China Electrotechnical Society，2015，30（22）：181-189.

［23］NOCEDAL J，WRIGHT S J.Numerical optimization［M］.New York，USA：Springer，2006：529-561.