概率粗糙集模型在推荐算法中的应用

陈功平,王 红

六安职业技术学院 信息与电子工程学院,安徽 六安 237158

概率粗糙集模型在推荐算法中的应用

陈功平,王 红

六安职业技术学院 信息与电子工程学院,安徽 六安 237158

推荐算法能够挖掘用户的潜在兴趣将项目自动地推荐给客户，是解决信息过载的智能手段之一。由于网络中的用户数和项目数较多，评分矩阵的稀疏性严重影响了推荐效果，推荐的先验知识缺失严重。粗糙集是一种可以使用不完备的知识实施推理的有效方法，使用概率粗糙集的α、β阈值合理划分边界域，生成推荐策略，降低评分矩阵稀疏性对推荐结果的影响。实验结果表明：概率粗糙集模型能够有效提高在评分矩阵非常稀疏的情况下的推荐准确率，其在Movie Lens数据集上的推荐准确率最高达到92.80%，覆盖率最高达100%。

概率粗糙集;推荐算法;参数学习

网络的普及应用让人们习惯于从网络上获取信息，而随着网络资源的爆炸式增长，使得用户耗费在无用信息上的时间和精力越来越多。推荐系统[1]能够从用户的历史行为中挖掘用户兴趣，将和用户兴趣相关的项目主动的推荐给用户，减少检索时间。近年推荐算法得到了学者的广泛关注和研究，其应用也得到各大网站的支持。

基于内容的推荐[2]（Content-Based Recommendation）、基于知识的推荐[3]（Knowledge-Based recommendation）、基于协同过滤的推荐[4]（Collaborative Filtering-Based Recommendation）等是常用的推荐算法，协同过滤推荐算法是一种简单且常用的算法，能够很好的与其他算法融合，是亚马逊等商业网站推荐系统的核心算法。协同过滤推荐算法从用户的历史行为中学习规律，挖掘用户喜好，然后预测用户对未关联的项目的喜好程度，将用户最喜爱的Top-n项目生成推荐列表提供给用户。

用户对项目的评分能很好的反映用户对项目的感兴趣程度，由于网络中的用户和项目数量非常多，导致评分矩阵十分稀疏，降低推荐效果。粗糙集[5]是一种可以利用不完备知识实施推理的有效方法，将稀疏的评分矩阵作为粗糙集的属性库，使用粗糙集思想合理划分等价类，从评分矩阵中挖掘规则实施推荐，提高推荐的效果。

实验表明，推荐模型在100 k Movie Lens数据集上的准确率和覆盖率最高达到92.80%和100%，比Pawlak粗糙集模型的性能更优。

1 概率粗糙集模型

概率粗糙集模型是Pawlak粗糙集模型的扩展，使用α、β参数细化Pawlak粗糙集模型的正域、负域和边界区域而得到的一种粗糙集模型[6]。

1.1 Pawlak粗糙集模型

Pawlak模型定义了上、下近似集合，设U表示论域，R是U的一个等价关系，即将U划分为多个不相交的R子集，可表示为U/R=｛R1,R2,…,Rn｝，现有X集合为U的子集，即，X⊆U，使用等价关系R来近似X，X的上近似和下近似[7]被定义如公式（1）～（2）。

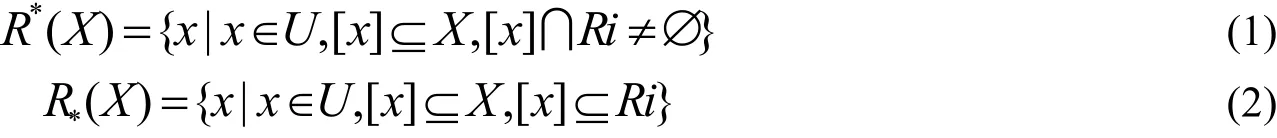
其中，[x]是X的一个划分，Ri是R集合中的一个子集，即，Ri⊆R。X集合下近似与上近似的比值称为集合X的粗糙程度。

显然0≤P(X|R)≤1，当P(X|R)=1时，集合X相对于等价关系R是精确的，当P(X|R)＜1时，集合X相对于等价关系R是粗糙的。

根据X的上下近似，可以将U划分为不相交的正域、负域和边界域，定义公式[8]见（4）～（6）。

正域、负域和边界域的关系如图1所示。整个区域表示论域U，圆表示要近似的集合X，矩形表示等价关系R，粗线实心矩形区域是X的下近似，即正域，虚线区域（去掉正域）是X的边界域，虚线外的区域是X的负域。

图1 正、负和边界区域的关系Fig.1 The relation of positive、negative and boundary regions

1.2 概率粗糙集模型

从图1可以看出，正域、负域是相互独立的，而边界域中，有的相交部分多，有的相交部分少，定义P(X/Ri)表示集合X与Ri等价关系的重叠程度[9]。

因此，可以使用P(X/Ri)来进一步细化X的上下近似以及正域、负域和边界域，设置两个参数α、β作为细化指标，定义[10]如公式（8）～（12）所示。

当参数α=1，β=0时，概率粗糙集等价于Pawlak粗糙集，当α＜1、β＞0时，Pawlak粗糙集的部分边界域将划分到正域和负域中，当参数α=β时，边界域将全部划分到正域或负域中。

2 基于粗糙集的推荐模型

基于粗糙集的推理需要从信息表中学习推理策略，表1可以看成一个基于评价矩阵的信息表，这里将评价1～3作为条件属性，总体评价作为决策属性，即，通过分析评价1、评价2、评价3和总体评价之间的关系，预测新用户对总体评价的结果。

表1 满意度调查表Table 1 Table of satisfaction survey

2.1 构造等价类

将表1条件属性（评价1～3）取值相同的用户归类到同一个关系（等价类），等价类结果如表2的第1列所示，R1～R4表示等价类的名称，花括号中的阿拉伯数字表示用户编号。

表2 基于表1的等价类构造及条件概率计算Table 2 Equivalence class construction and conditional probability calculation on Table 1

2.2 计算决策概率

从表1～2可以得到，R1等价类的总体评价均为+，按照粗糙集推理策略，若有新用户划分到R1类，新用户总体评价为+的概率为100%；R2类中，总体评价全部为-，因此R2类总体评价为+的概率为0；R3类中3、7、9用户的总体评价为+，10用户的总体评价为-，所以R3类的总体评价为+的概率为3/4=75%。以“总体评价”为+作为条件，每个等价类决策属性为+的概率值结果见表2的第2列。

经过等价类构造和决策概率计算，总体评价属性的决策表如表3所示。

表3 总体评价的决策表Table 3 Decision of overall assessment

2.3 评价指标

推荐时，找不到等价类的样本，即无先验知识的样本无法完成推荐；概率粗糙集推荐模型中的边界域样本虽然能够找到等价类，但因位于边界域所以也无法完成推荐。使用准确率Precision、覆盖率Coverage和二者的F-Score值作为推荐效果的评价指标，三个评价指标的计算公式如（13）～（15）所示。

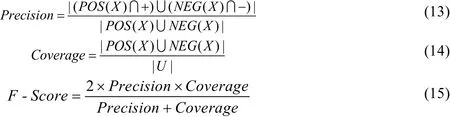
Precision是正域样本推荐为+、负域样本推荐为-的数量之和与正域、负域样本总数量的比值，即推荐正确样本数和能够完成推荐的样本数的比值；Coverage是正域、负域样本数之和与总样本数的比值，即能够完成推荐的样本数与参加推荐的总样本数的比值；通常情况下这两个比值是互相制约的，因此使用F-Score值考察推荐结果的优劣。

按照粗糙集推理规则，将划分到正域中的等价类的总体评价预测为+，划分到负域中的等价类的总体评价预测为-，当α=1，β=0时，由表3的决策表可得到概率粗糙集的三个区域分别为：POS1,0(X)=R1，NEG1,0(X)=R2，BND1,0(X)=R3∪R4，边界域无法预测，即可以为R1和R2等价类预测，无法为R3和R4等价类预测，R1类预测为+、R2类预测为-，所以预测的准确率Precision=100%，但只能为1、2、4、6号共4个用户预测，预测的覆盖率Coverage=4/10=40%，F-Score=57.1%。

当α=0.6，β=0时，三个区域分别为：POS0.6,0(X)=R1∪R3，NEG0.6,0(X)=R2，BND0.6,0(X)=R4，此时预测的准确率Precision=7/8=87.5%，覆盖率Coverage=8/10=80%，牺牲了12.5%的准确率，提高了40%的覆盖率，F-Score=83.6%。

若α、β都取0.5，则边界域为空，即Coverage=100%，Precision=8/10=80%，F-Score=88.9%。在实际应用中，α、β参数通过学习获得具体取值。第3节介绍概率粗糙集模型中决策表训练和参数学习算法。

3 决策表构造和参数学习算法

将评分矩阵中的积极评分（+）标记为1，消极评分（-）标记为-1，无关项标记为0，将Precision、Coverage作为评价标准，使用训练数据集Train构造基于概率粗糙集推荐模型的决策表、学习最优的参数α、β，然后通过测试数据集Test验证推荐模型的推荐效果。

3.1 属性约简

定义U={ui|i=1,…n}表示用户集，I={ij|j=1,…m}表示项目集，项目可以是商品、电影、新闻等，评分矩阵R={rij|i=1,…n,j=1,…m}表示用户与项目之间的历史行为。为了使得算法能够适用于全数据集的推荐，因此要为所有的项目都构造出一份有用的决策表，当学习项目ij的决策表时，项目ij的有效评分作为决策属性，项目ij以外的项目评分作为条件属性，由于评分矩阵中的项目数量多，因此初始时条件属性有m-1个，条件属性数量过多不利于等价类的构造和测试时的匹配搜索，因此要减少条件属性的数量，即属性约简。

将初始的m-1个条件属性中有效评分最多的前N项属性作为条件属性，对于不同的数据集，N的取值不同，需要通过训练学习得到。

3.2 决策表构造和参数学习

基于全数据集的决策表构造和参数学习算法见算法1所示。

算法1决策表构造和参数学习

输入：训练集评分矩阵Train，N，α'，β'

输出：等价类Equi_Class及对应参数α、β

1.从Train中提取项目i的非0评价矩阵Train(i)

2.从Train(i)中提取除项目i外、有效评价数量最多的前N个项目的评价数据及项目i的评价数据，存入Info_Table(i)

3.从Info_Table(i)中提取项目i的等价类表Equi_Class(i)

4.α（i）=1，β（i）=0

5.α（i）-=0.01，直到α（i）＜α'或Precision(i)＜88%和Coverage(i)＜88%

6.β（i）+=0.01，直到β（i）＞β'或Precision(i)＜88%和Coverage(i)＜88%

4 实验结果分析

使用100 k的Movie Lens[11,12]数据集验证文中提出的推荐算法，数据集中存储电影评分记录10万条，每条记录由用户id、电影id和评分值三项构成，评分值为1～5的整数，评分记录情况如表4。

表4 评分表简介Table 4 Introduction of rating

将100 k的数据按照8:2的比例划分为训练集Train和测试集Test，因部分电影的评分记录较少，所以有些电影只出现在Train或Test中。

4.1 N值的训练

以Train中有效评分较多的1号和50号电影为例，表5列出的是当N值分别设置为5、8、10、15时，得到的等价类数量与条件属性N值的关系。

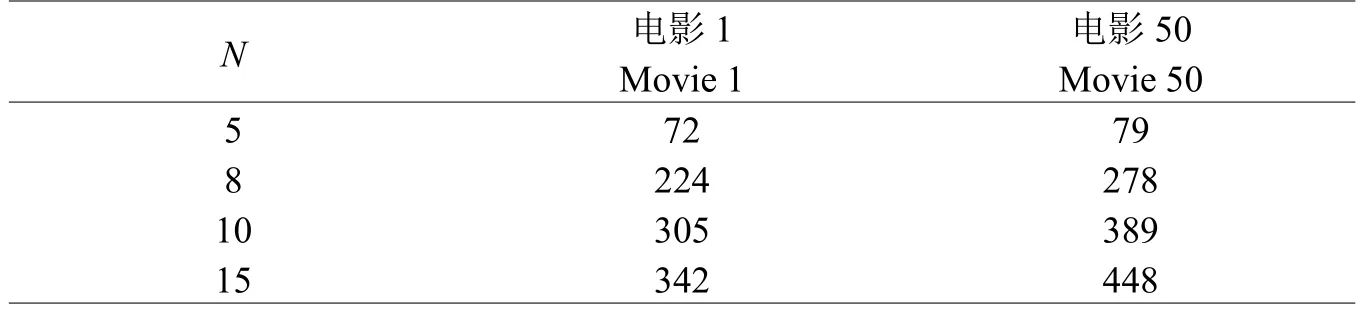
表5 N与等价类数量的关系Table 5 Relationship between N and the number of equivalent classes

N=15时，等价类个数与Train(i)的行数差值很小，即能够被划分到同一等价类的用户量非常少，则划分的集合粗糙度小，失去粗糙集推荐的意义；N=10，等价类个数降低不明显；N=5，等价类数量减少迅速，用来划分集合，粗糙度相对较高；若N值再降低，将导致粗糙程度加大，不利于推荐，因此N可设置为5到10之间的整数。

4.2 参数学习结果

评分表中的实际评分值为1～5的整数，为了适应粗糙集推荐模型，将5级评分简化为2级评分，设置划分值γ，γ=1，表示评分值1标记为-1，其余有效评分值标记为1；γ=2，表示1、2分标记为-1，其余有效评分值标记为1，以此类推。

当α'=β'=0.5（后文无特别说明，α'、β'均设置为0.5）、γ=2时，参数学习后，α、β、准确率、覆盖率、F-Score的平均值如表6所示。

表6 训练集训练指标Table 6 Training index of Train

从表6可见，训练集的平均准确率和覆盖率指标都在90%以上。

4.3 测试结果与分析

4.3.1 测试结果分析 表7是划分值为1时概率粗糙集模型的推荐效果。

表7 N=1时的推荐效果Table 7 Recommended effect of N=1

表中Precision=CCI/(CCI+ECI)，Coverage=(CCI+ECI)/(NF+CCI+BI+ECI)。由表7可见，N值越大，找不到等价类的记录越多，当N=5时，Test集合的总体评价值最优，经验证，对其他划分值N取5时评价值都是最优，后文无特别说明N值取5。

图2是划分值分别取1、2、3、4，Test集合推荐效果比较，当划分值取1时效果最优，取3时效果最差，准确率只有58.77%，整个模型的覆盖率指标都非常高，为了提高推荐精确度，可以牺牲一定数量的覆盖率指标值。

图2 不同N的推荐效果比较Fig.2 Recommended effect comparison of different N

4.3.2 与Pawlak粗糙集推荐模型的比较 Pawlak粗糙集模型可以使训练集的推荐准确率达到100%，表8是Test和Train集合划分值分别取1、2、3、4时的三项指标值。

表8 Pawlak粗糙集模型与概率粗糙集模型性能比较Table 8 Recommended effect comparison between Pawlak and probabilistic rough set

Model列中A表示“Pawlak粗糙集模型”，B表示“概率粗糙集模型”，由数据可见，在划分值相同时，准确率差值较小，Test集合的最大差值不到3%，覆盖率差值较大，Test集合的最大差值达到35%，可见，概率粗糙集模型和综合指标优于Pawlak粗糙集模型。

图3是Test集合不同划分值的各项指标比较。

图3 Test集合不同N的评价指标比较Fig.3RecommendedeffectcomparisonofTestunderdifferentN

图4 Train集合不同N值的评价指标比较Fig.4RecommendedeffectcomparisonofTrainunderdifferentN

P1、C1、F1和P2、C2、F2分别表示Pawlak模型和概率粗糙集模型下Precision、Coverage、F-Score指标的值。Train集合不同划分值的各项指标比较(图4)。

4.3.3 α'和β'对结果的影响 为了提高推荐准确率，应提高参数α的值，从表8可以看出，整个推荐的覆盖率指标较好，即参数β可以不调整。将α'和β'的值平滑变化，经实验验证，即使将β'的值设置较高，实际得到的β都不会超过0.5，而α'的值对α影响较大，最后得到的α与α'接近。

划分值取2，Test集合的预测结果如表9所示。

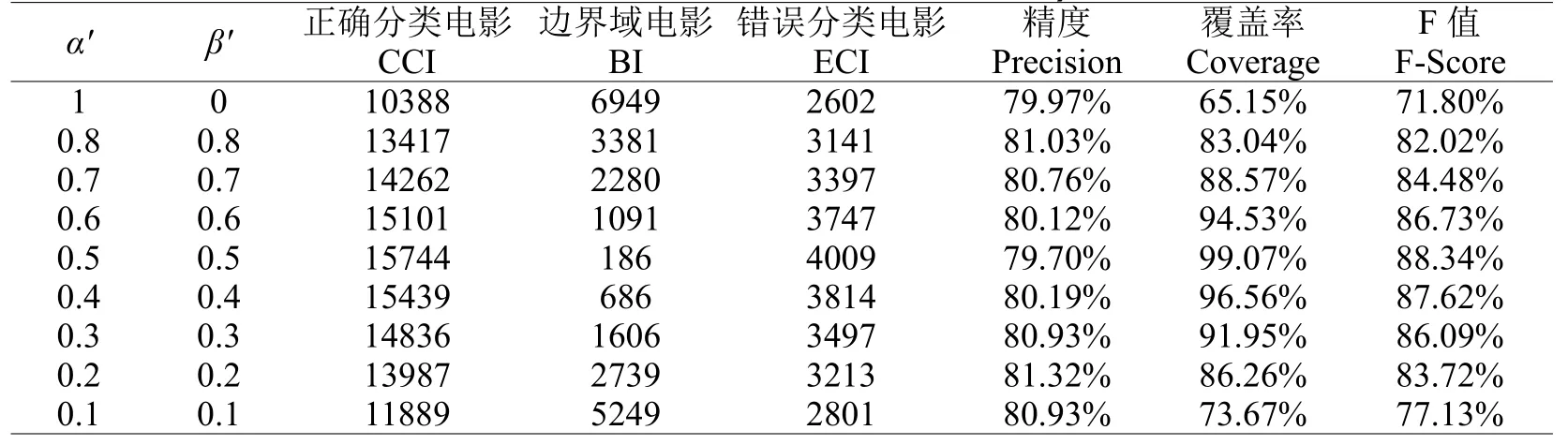
表9 α'和β'对结果的影响Table 9 Recommended effect of α'and β'

当α'取1、β'取0时，边界域的数量最多；α'和β'都取0.5时，边界域数量最少，所以推荐的覆盖率指标较高。

5 结语

使用概率粗糙集理论中的α、β参数将粗糙集中的边界域分配到正域和负域中，可以降低评分矩阵稀疏性对推荐精度的影响，采用α、β参数逐步逼近、保证推荐准确率和覆盖率指标的参数学习算法，有效的提高了推荐效果，比Pawlak粗糙集模型的性能更优。粗糙集推荐模型的边界域是无法实施推荐的，可以结合其他推荐算法，进一步提高推荐效果。

[1]Guan Y,Cai SM,Shang MS.Recommendation algorithm based on item quality and user rating preferences[J].Frontiers of Computer Science,2014,8(2):289-297

[2]Lops P,Gemmis MD,Semeraro G,et al.Content-based and collaborative techniques for tag recommendation:an empirical evaluation[J].Journal of Intelligent Information Systems,2013,40(1):41-61

[3]Liu XC,Zhou JC.Research on Knowledge-based Personalized Recommendation Service System Retrieval Service[J]. Energy Procedia,2011,13(4):10103-10108

[4]孙光福,吴 乐,刘 淇,等.基于时序行为的协同过滤推荐算法[J].软件学报,2013,24(11):2721-2733

[5]Liu D,Li TR,Zhang JB.Incremental updating approximations in probabilistic rough sets under the variation of attributes[J].Knowledge-Based Systems,2015,73(1):81-96

[6]Ma XA,Wang GY,Yu H,et al.Decision region distribution preservation reduction in decision-theoretic rough set model[J].Information Sciences,2014,278(10):614-640

[7]Azam N,Yao JT.Game-theoretic rough sets for recommender systems[J].Knowledge-Based Systems,2014,72(1):96-107

[8]陈 昊,杨俊安,庄镇泉.变精度粗糙集的属性核和最小属性约简算法[J].计算机学报,2012,35(5):1011-1017

[9]徐久成,李晓艳,孙林.一种基于概率粗糙集模型的图像语义检索方法[J].南京大学学报:自然科学版,2011,47(4):438-445

[10]王兆浩,舒 兰,丁修勇.几种粗糙集模型的推广研究[J].计算机工程与应用,2011,47(36):68-72

[11]袁汉宁,周 彤,韩言妮,等.基于MI聚类的协同推荐算法[J].武汉大学学报:信息科学版,2015,40(2):253-257

[12]田谦益,王小北.基于Memetic框架混合群智能算法的NARMAX模型参数辨识[J].山东科技大学学报:自然科学版,2013,32(1):88-94

Application of Probabilistic Rough Set Model in Recommendation Algorithm

CHEN Gong-ping,WANG Hong
College of information and Electronic Engineering/Lu’an Vocation Technology College,Lu’an 237158,China

Recommendation algorithm can dig into the potential interest of users and then automatically recommends the project to the users.It is one of the intellectual approaches solving the information overload.As the number of users and number of items are more,the sparseness of rating matrix has a strong impact on the effect of recommendation.The priori knowledge of recommendation is missing seriously.Rough set is an effective method which can adopt an incomplete knowledge to carry out ratiocination.It proposes dividing the boundary region by using probabilistic rough set threshold α and β,creating recommendation strategy and reducing the effect of the sparseness of score matrix to the recommendation result.The experimental results indicated that the model of probabilistic rough set could improve the recommendation accuracy rate under the circumstance of the high sparseness of score matrix.The recommendation accuracy rate could be up to 92.80%in the Movie Lens data sets and the highest fraction of coverage could be up to 100%.

Probabilistic Rough Set;recommendation algorithm;parameter learning

TP301

:A

:1000-2324(2017)02-0192-07

10.3969/j.issn.1000-2324.2017.02.006

2015-05-22

:2015-11-20

2015年度安徽高校自然科学研究重点项目(KJ2015A435);安徽省2016年高校优秀青年人才支持计划重点项目(gxyqZD2016570);安徽省2014年高校优秀青年人才支持计划

陈功平(1980-),男,硕士研究生,讲师.研究方向:个性化推荐，网络技术.E-mail:chgp06@126.com

*通讯作者:Author for correspondence.E-mail:wh0115140@126.com