基于正交非负矩阵分解的高光谱遥感图像混合像元分解

孙 莉,赵庚星

1.山东农业大学 信息科学与工程学院,山东 泰安 271018

2.山东农业大学 农业资源与环境博士后科研流动站,山东 泰安 271018

基于正交非负矩阵分解的高光谱遥感图像混合像元分解

孙 莉1,2,赵庚星2

1.山东农业大学 信息科学与工程学院,山东 泰安 271018

2.山东农业大学 农业资源与环境博士后科研流动站,山东 泰安 271018

像元分解是遥感图像信息挖掘的重要手段，非负矩阵分解模型应用于高光谱遥感图像混合像元分解时，分解的效果与算法所获局部最优解密切相关。本文将带正交性约束的非负矩阵分解用于光谱解混，保证了分解矩阵列向量的线性无关性，进而使分解所得端元光谱具有较大的独立性。通过试验分析，利用正交非负矩阵分解，实现了对1997年机载可见光及红外成像光谱仪(AVIRIS)高光谱图像的混合像元分解，结果表明，增加约束条件后的正交非负矩阵分解，能成功分离出6种端元光谱，解混出的端元光谱与参考光谱的光谱角距离更小，与真实地物的丰度谱图吻合度增强。

非负矩阵分解;高光谱遥感图像;混合像元分解

高光谱遥感图像由航天、航空载体上的高光谱成像仪获得，它具有高光谱分辨力的特点，可在几百、上千个连续光谱波段获取目标图像。高光谱遥感图像的主要优势是它的图像数据可视为三维图像，即二维图像加一维光谱信息。二维图像描述地表被测物空间信息特征，一维光谱信息揭示每一像元的光谱曲线特征。由于遥感图像空间分辨率的限制以及地物的复杂多样性，一个像元内往往会包含多种地物类型(混合像元)，为了提高光谱遥感图像对真实地表覆盖的描述准确性，需要对图像进行混合像元分解。

近年来，非负矩阵分解(Nonnegative Matrix Factorization,NMF)被逐渐引入混合像元分解中，为基于线性光谱混合模型的混合像元分解提供了新的途径。若仅满足线性光谱模型的非负性限制条件，NMF的求解不具有唯一性，这是由NMF所转化的目标函数的非凸性所导致的，一般优化算法只能找到其局部最优解。文献[1,2]将没有附加任何条件的NMF直接应用于光谱解混，并针对模拟数据进行实验取得了一定的结果，由于局部最优解的限制，真正用于高光谱数据时效果不佳。针对NMF在高光谱混合像元分解的具体应用，已有学者尝试通过增加有效的约束条件，改进上述局限性。Jia S.等[3]在NMF模型中增加了稀疏性和分段平滑性约束，Miao L.提出了最小体积约束的NMF[4]，吴波等[5]以端元光谱之间的差距为约束条件，问题模型综合了图像的分解误差和端元光谱的影响。赵春晖等[6]提出了以最小估计丰度协方差和单形体各顶点到中心点均方距离总和最小约束的NMF，杨秀

坤等[7]引入端元光谱数学期望的四阶累积量和负熵约束，在问题模型中加入了端元独立性约束。研究结果表明，增加特定约束条件后，对高光谱图像进行解混，可取得较好的分类效果。

在非负矩阵分解模型中加入正交性约束，称之为正交非负矩阵分解(Orthogonal Nonnegative Matrix Factorization,ONMF)。本文将ONMF应用于高光谱混合像元分解，从数据处理的角度解释了增加正交性约束的优势，即保证分解所得端元光谱的独立性。同时，利用NMF、ONMF与K-均值和球形K-均值的等价关系，分析了四种方法进行特征提取的优缺点。数值结果表明，利用ONMF可成功完成对机载可见光及红外成像光谱仪(AVIRIS)采集的Urban区域高光谱图像的混合像元分解。ONMF解混出的端元光谱与USGS谱库的真实光谱间的光谱角更小，同时，与真实地物的丰度谱图吻合度较之NMF明显增强。

1 非负矩阵分解与光谱解混

1.1 非负矩阵分解

Lee D.D.和Seung H.S.提出非负矩阵分解的思想，对于现有的大规模矩阵Wn×m，NMF算法旨在寻找非负矩阵Un×r和Vr×m，使得W≈UV，其中W,U,V均为非负矩阵，最终通过两个低秩矩阵U和V近似W。NMF在处理大规模数据时所体现出的优势是其它传统矩阵分解算法所无法比拟的。事实上，NMF模型可以转化为如下具有非负界约束的优化问题，

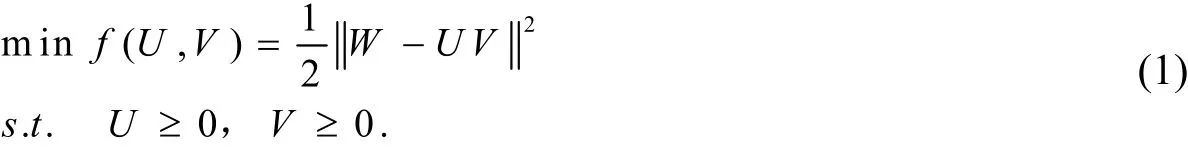
其中，ǁ·ǁ代表Frobenius范数，U≧0，V≧0表示矩阵U和V所有元素均为非负数。

1.2 光谱解混中的非负矩阵分解

高光谱图像可以看成是三维数据构成的立方体，它的X和Y维表现的是地球表面的坐标，第三维是波段，它由光波的频率所决定，实际的数据是地球上的特定位置在某一波长下的强度。立方体的顶层对应长的波长数据，底层数据对应短的波长数据。例如，将一幅AVIRIS图像读取为s×t×m的矩阵，其中m对应波段数，s×t对应图像的宽度和高度，不妨设图像的像素点有n=s×t个。将上述矩阵重新排列后，可得到n×m的矩阵W。

利用NMF实现W的分解后，得到的矩阵Un×r为丰度矩阵，这里r对应光谱图像中端元的个数，U的列向量分别对应某个端元的空间分布。Vr×m则为端元矩阵，它的行向量为某个端元的光谱向量。

2 正交非负矩阵分解

2.1 问题模型

Ding[8]首先提出了ONMF，已有学者证明ONMF与K-均值聚类等价，研究表明对V增加正交性约束后，ONMF等价于对W按列聚类[9]。ONMF的问题模型可描述如下，

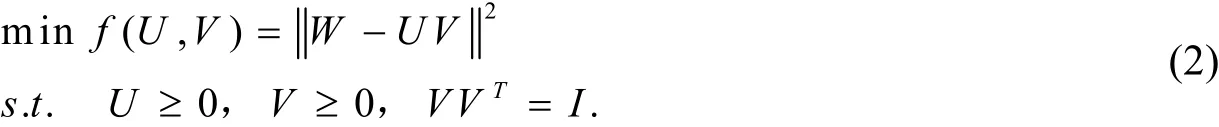
这里I表示r×r的单位矩阵。ONMF可视为增加正交性约束后的NMF问题，V增加正交性约束后，在高光谱数据处理中具有更好的优势。

2.2 正交约束在光谱解混中的优势

ONMF问题模型(2)中，正交约束条件VVT=I一旦满足，V的行向量便保持了正交关系，易推知V的行向量是线性无关的。由于V的行向量对应端元光谱，正交约束的满足保证了端元光谱具有较大的独立性。

文献[10]，证明了ONMF问题(2)与球形K-均值问题等价。事实上，利用K-均值和球形K-均值可实现光谱解混的第一步工作——端元提取。K-均值聚类算法采用均值作为某类的代表点，当类间的大小差别较大时，通过分割以达到极小化目标函数的目的，这会导致错误的聚类结果。球形K-均值以最大化相同类中数据点的相似度为目标，可以很好的克服上述K-均值的缺陷。NMF和ONMF与K-均值和球形K-均值相比，优势在于前两个方法可以同时完成端元提取和混合像元分解的工作，而后者在获知端元光谱后，需要与其它方法结合，进一步求解描述端元分布的丰度矩阵。

3 试验分析

3.1 遥感数据

文中数据取自1997年机载可见光及红外成像光谱仪(AVIRIS)采集到的Urban高光谱图像（307×307像素），有210个波段。该地区包含了屋顶、草地、树木、道路等多种地物的混合，适用于检验算法对于高混合度数据的适应能力。去除信噪比低和水蒸气吸收波段(1～4,76,87,101～111, 136～153以及 198～210)，余下162个有效波段。图1为第53,35,10波段图像合成的伪彩色图像。

图1 Urban区域的AVIRIS数据伪彩色图Fig.1 AVIRIS data pseudo-color image of Urban Area

3.2 结果分析

首先设置端元数目为6，即r=6，分别采用正交非负矩阵分解(ONMF)和非负矩阵分解(NMF)，对Urban数据进行高光谱混合像元分解。利用文献[11]给出的有效集型算法求解NMF问题模型，ONMF则采用文献[12]给出的乘性迭代公式进行矩阵更新。图2中，第1行的6个图像反映了Urban区域的真实丰度谱图，第1-6列分别对应路面，草地，树木，屋顶，金属以及裸地。ONMF解混结果显示在第2行，第3行则是NMF实现的解混结果。从图中可以看出，ONMF有效分离了草地，树木，屋顶，金属以及裸地的丰度谱图，路面的丰度谱图不理想。采用NMF实现的解混结果，其中仅能有效提取树木，屋顶，裸地三者的丰度谱图，路面、草地、金属的分离效果不明显。

图2 Urban区域的AVIRIS数据解混后丰度谱图对比Fig.2 Comparison of the abundance map obtained by NMF and ONMF

另一方面，取定类别数为6，即k=6，利用K-均值和球形K-均值算法对上述相同的162个波段的高光谱数据进行处理，可获得6个聚类中心(特征光谱信息)。

我们将美国地质调查局(USGS)库中的对应光谱作为参考光谱，计算ONMF、NMF、K-均值、球形K-均值分离出的特征光谱与真实地物光谱之间的光谱角距离(Spectral Angel Distance,SAD)。通过SAD计算出的角度越小代表特征提取出的端元光谱与参考光谱越匹配。光谱角的计算公式为，其中 Va, Vb表示不同端元的光谱向量。

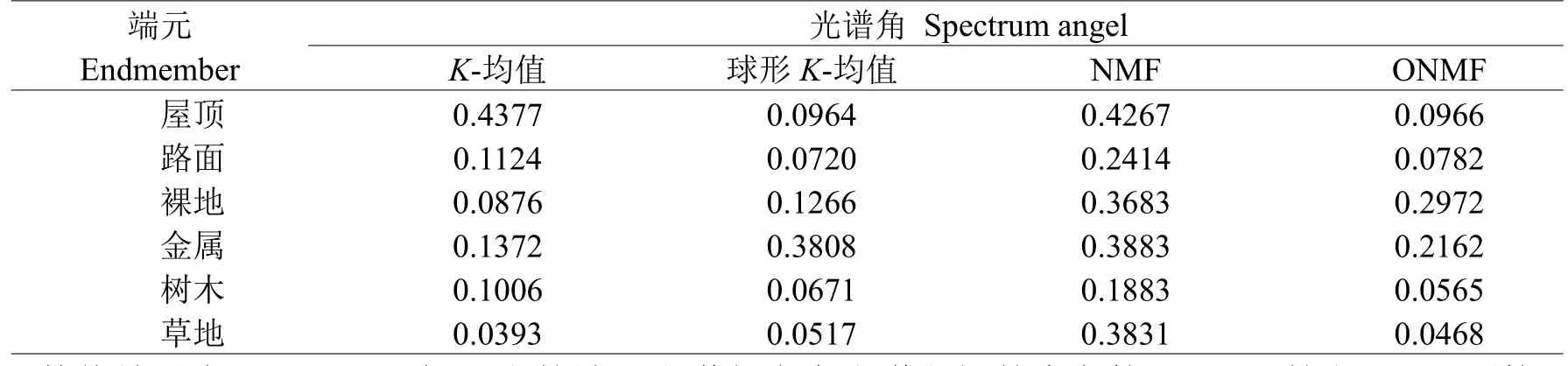
表3 AVIRIS数据USGS谱库的真实光谱和估计的端元光谱的SAD比较Table 3 SAD comparison for the real AVIRIS data in USGS and estimated endmember spectrum

数值结果表明，ONMF提取出的端元光谱与参考光谱之间的夹角接近于0，较之NMF更接近真实端元光谱。通过ONMF进行端元提取的精度与球形K-均值相当，较之K-均值和NMF实现的端元提取，精度明显提高。

4 结语

非负矩阵分解和基于线性光谱混合模型的混合像元分解相符合，通过NMF分解所得的U和V分别对应丰度矩阵和端元矩阵。利用NMF处理高光谱数据，可同时实现端元提取和混合像元分解工作。由于局部最优解的限制，NMF应用于高光谱数据时效果不佳。通过对NMF问题模型增加特定的约束条件，在一定程度上可以提高分解结果的有效性。

在非负矩阵分解模型中加入正交性约束，称之为正交非负矩阵分解。从高光谱数据处理的角度看，正交性约束保证了分解矩阵中端元光谱的独立性。数值结果表明，ONMF与球形K-均值实现的端元提取精度相当，比通过NMF和K-均值提取的端元光谱更接近真实端元光谱。同时，与球形K-均值相比，ONMF分解获得的矩阵U同时给出了每个端元的空间分布。本文方法较好改善了NMF的处理效果，为高光谱混合像元分解提供了有效手段。

数值测试过程中，求解NMF的有效集型算法较之其它求解算法，数值结果更好，我们将进一步研究有效集指标与光谱解混相关指标的对应关系，并设计求解ONMF问题的有效集型算法。

[1]Sajda P,Du S,Parra L.Recovery of constituent spectra using non-negative matrix factorization[C].Proc.SPI E:The International Society for Optical Engineering,2003,5207:321-331

[2]Pauca VP,Piper J,Plemmons RJ.Nonnegative matrix factorization for spectral data analysis[J].Linear Algebra Appl., 2006,416(1):29-47

[3]Jia S,Qian Y.Constrained nonnegative matrix factorization for hyperspectral unmixing[J].IEEE Trans.Geosci.Remote Sens.,2009,47(1):161-173

[4]Miao L,Qi H.Endmember extraction from highly mixed data using minimum volume constrained nonnegative matrix factorization[J].IEEE Geosci.Remote Sens.,2007,45(3):765-777

[5]吴 波,赵银娣,周小成.端元约束下的高光谱混合像元非负矩阵分解[J].计算机工程,2008,34(22):229-230,233

[6]赵春晖,成宝芝,杨伟超.利用约束非负矩阵分解的高光谱解混算法[J].哈尔滨工程大学学报,2012,33(3):377-382

[7]杨秀坤,王东辉.利用独立性约束非负矩阵分解的高光谱解混算法[J].哈尔滨工程大学学报,2014,35(5):637-641

[8]Ding C,Li T,Peng W,et al.Orthogonal nonnegative matrix t-factorizations for clustering[C].In:KDD’06:Proc.12thACM SIGKDD Internet.Conf.on Knowledge Discovery and Data Mining.ACM,2006:126-135

[9]YangZ,OjaE.Linearandnonlinearprojectivenonnegativematrixfactorization[J].Trans.Neural Netw.,2010(21):734-749

[10]Pompili F,Nicolas G,Absil P,et al.Two algorithms for orthogonal nonnegative matrix factorization with application to clustering[J].Neurocomputing,2014(141):15-25

[11]Kim J,Park H.Fast nonnegative matrix factorization:an active-set-like method and comparsions[J].SIAM Journal on Scientific Computing,2011,33(6):3261-3281

[12]LiZ,WuXD,PengH.Nonnegativematrixfactorizationonorthogonalsubspace[J].PatternRecognitionLetters,2010(31):905-911

Decomposition of Mixed Pixels of Hyperspectral Remote Sensing Images Based on Orthogonal Non-negative Matrix Factorization

SUN Li1,2,ZHAO Geng-xing2
1.College of Information Science and Engineering/Shandong Agricultural University,Tai’an 271018,China
2.The Post-doctorate Research Station of Agricultural Resources and Environment/Shandong Agricultural University,Tai’an 271018,China

Hyperspectral unmixing is a powerful tool for the remote sensing image mining.Nonnegative matrix factorization (NMF)has been adopted to deal with this issue,while the precision of unmixing is closely related with the local minimizer of NMF.Orthogonal NMF which imposes orthogonality constraints on the factor matrices can improve the clustering performance,since it ensures the independent of the endmember spactra.In the experimental test,ONMF was used to unmix the Urban scene which was captured by airborne visible/infrared imaging spectrometer(AVIRIS)in 1997,numerical results showed that ONMF could extract the endmember signature and accurately estimate abundance maps.

Nonnegative matrix factorization;hyperspectral remote sensing image;decomposition of mixed pixels

O221;TP751.1

:A

:1000-2324(2017)02-0264-04

10.3969/j.issn.1000-2324.2017.02.021

2016-01-09

:2016-02-23

国家自然科学基金(41271235,10901094,11301307);“十二五”国家科技支撑计划(2013BAD05B06-5);山东省优秀中青年科学家科研奖励基金(BF2011SF024,BF2012SF025);山东省高等学校科技计划项目(J16LI16)

孙 莉(1980-),女,博士,讲师,研究方向为最优化算法与理论.E-mail:sunli@sdau.edu.cn

*通讯作者:Author for correspondence.E-mail:zgx@sadu.edu.cn