汽车非线性悬架系统的稳定性分析
2017-05-22成洁
成 洁
(武警后勤学院,天津 300309)
汽车悬架系统是典型的非线性系统,非线性振系中可有不止一个平衡点(定点,奇点),其中有些可能是稳定的,另一些则可能是不稳定的。对于悬架系统,选取不同的系统参数会使系统具有不同的稳定性,因此有必要研究非线性悬架系统在周期外力扰动下的稳定性。
1 力学模型及运动微分方程
以研究垂直振动为目的建立汽车的动力学模型,本文采用1/4车体模型分析车辆特性。这里只考虑悬架弹簧的非线性刚度特性。变刚度弹簧的回复力-位移关系可表示为[1]:

式中:Fs为弹簧回复力,k为弹簧刚度,x为弹簧位移,ε为一表示弹簧非线性程度的小参数,ε=0时,该弹簧为线性。其力-位移关系曲线如图1所示,虚线代表线性弹簧的回复力-位移曲线,实线代表非线性弹簧的回复力-位移曲线。
图 2为悬架系统的力学模型。其中 m2为簧载质量,m1为非簧载质量,k1为轮胎刚度,c2为减振器粘性阻尼系数,z2为簧载质心垂直位移,z1为非簧载质心垂直位移,z0为路面不平激励,F(z2- z1)为非线性弹性力。

图1 变刚度弹簧力—位移曲线

图2 两自由度悬架振动模型
系统的运动微分方程为:
式中:——簧载质心的速度和加速度;——非簧载质心的速度和加速度。
选取下述状态变量:

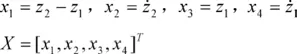
有下列方程:

选取车身加速度,车轮动位移,悬架动扰度三个性能指标作为输出变量。

,乘以 k1后为车轮动载荷,x1= z2- z1为悬架动扰度。
2 悬架系统的稳定性分析
所谓解的稳定性[2],是指系统在扰动下能够自动返回原来的运动状态的性能。根据线性稳定性定理:如果非线性方程的线性化方程的定点是渐进稳定的,则参考点(态)xi0是非线性方程的渐进稳定解;如果线性化方程的定点是不稳定的,则参考态是非线性方程的不稳定解。
当状态变量的个数n>2时,系统在定态xi0邻域的的线性化方程可写成适量形式:

式中: 是n列(1×n)矢量,系数矩阵A取下面的形式:

方程(7)的基本解为:

代入方程(7),得:

齐次代数方程有非平凡解的条件是:
可写为如下形式:
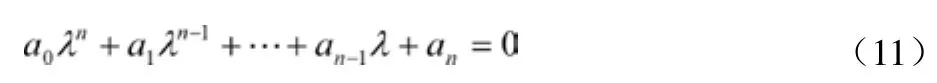
当方程(11)的所有特征值λi的实部Reλi都取负值时,解的每一项才收敛,这时定态才是渐进稳定的;反之,只要有一个特征值λi的实部取正值,定态就是不稳定的。

令,平衡点为(0,0,0,0),(0,0,±3.162i,0)(舍去)。对于平衡点(0,0,0,0)

所以在平衡点(0,0,0,0)处的特征方程为:
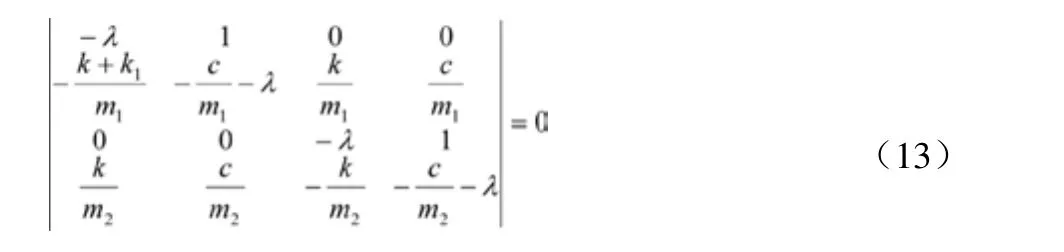

根据罗斯—霍维兹判据[3],△1>0,△2=0,所以平衡点是稳定的,但不是渐进稳定的。
在系统没有受到外界激励时,车身相轨线和车轮相轨线如图(3),(4)所示,分别由初始状态呈螺旋状回到平衡态。

图3 相平面上的轨线

图4 相平面上的轨线
当系统受到外界周期扰动激励时,令F=Asin(wt),ε=0.1(硬特性弹簧),悬架的结构参数为:m2=1091.49kg,m1=162.51kg,c=3235Ns/m,k=94835N/m,k1=1164593N/m。固定 A=0.5m,初始条件为x1=0,x2=0,让w在本文研究的时间频率范围内(0.5-30Hz)变化。
当w分别为9rad/s、30rad/s、85rad/s时,车身和车轮相轨迹分别如图5—10所示。可以看到,车身和车轮的相轨迹都分别从初始状态经暂态后绕定点(原点)旋转,成为一封闭的圆环。说明车身和车轮都在做稳定的周期震荡。

图5 相平面上的轨线

图6 相平面上的轨线
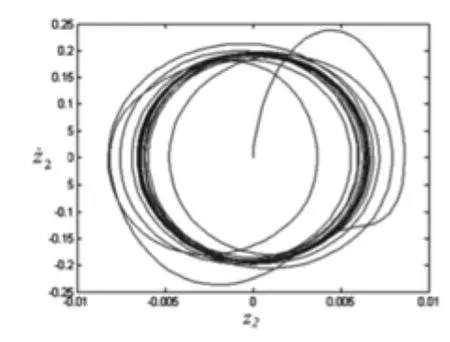
图7 相平面上的轨线

图8 相平面上的轨线

图9 相平面上的轨线

图10 相平面上的轨线
3 结论
汽车悬架系统的稳定性在分析汽车振动特性中至关重要,它是关于悬架特性一切研究的基础。本文结合实例分别对单自由度悬架系统和两自由度系统的稳定性作出分析,可以看到:在本文所研究的时间频率范围内(0.5Hz—30Hz,它能够覆盖汽车系统的车身、座位和车轮的固有频率范围),具有弱非线性的悬架系统是稳定的。
参考文献
[1] 张慧鹏.车辆非线性悬架系统动态特性[J].拖拉机与农用运输车,2007,(04)58-62.
[2] 刘秉正,彭建华. 非线性动力学.高等教育出版社,2004.1.
[3] 诸德超,邢誉峰主编.工程振动基础.北京航空航天大学出版社, 2014.
