热固耦合作用下的套管−水泥环−地层多层组合系统应力分析

赵新波，韩生超，杨秀娟，闫相祯,3，张立松

热固耦合作用下的套管−水泥环−地层多层组合系统应力分析

赵新波1,2，韩生超1，杨秀娟1，闫相祯1,3，张立松1

(1.中国石油大学(华东)储运与建筑工程学院，山东青岛，266580；2.青岛理工大学理学院，山东青岛，266033；3.中国石油大学(华东)油气CAE技术研究中心，山东青岛，266580)

考虑非均匀地应力、内压和地层高温对高温高压井套管−水泥环−地层多层组合系统的作用，应用弹性力学理论，结合边界条件、接触条件和连续条件，获得热固耦合作用下套管−水泥环−地层多层组合系统应力分布的解析解。讨论水泥环厚度、弹性模量、泊松比、地层温度、套管−水泥环层数对最内层套管内壁M ises应力分布规律的影响。研究结果表明：上述因素对最内层套管内壁M ises应力的分布均有影响；对比套管−水泥环−地层的单层和多层组合系统，多层组合系统的最内层套管内壁的M ises应力较单层系统明显降低，这说明多层组合系统具有重要的工程价值。

套管−水泥环−地层；热固耦合；多层组合系统；弹性力学

准确获取套管−水泥环−地层多层组合系统的应力分布对于防止套管损坏具有重要工程价值。现阶段，高温高压井(HPHT)越来越多，套管处于非均匀高地应力、高内压和高地层温度的联合作用下，这进一步加剧了套管的损坏，故开展热固耦合作用下的套管−水泥环−地层多层组合系统的受力特性分析具有重要价值。国内外学者取得了大量套管−水泥环−地层三层组合系统的受力特性研究成果。YIN等[1]基于弹性力学理论，研究了平面问题垂直井筒受地应力作用时的力学行为；殷有泉等[2−5]先后用弹性理论及数值方法求解得到井筒受地应力荷载问题的理论解，并研究了系统接触表面的应力分布规律；LAST等[6]对构造应力引起的套管位移进行了研究；李军等[7]用弹性理论及有限元方法对倾斜井组合系统受力进行了研究。前人的研究大多基于套管−水泥环−地层三层组合系统，难以将研究结果直接应用于实际的多层套管受力分析。王宴滨等[8]研究了套管−水泥环−地层多层组合系统受力特性，然而未考虑地层温度的作用，并不能直接用于高温高压井多层组合系统受力特性分析。基于此，本文作者以套管−水泥环−地层多层组合系统为对象，应用弹性力学方法，考虑热固耦合作用，获取多层组合系统在非均匀地应力下的应力分布规律，并讨论水泥环厚度、水泥环弹性模量、水泥环泊松比、套管−水泥环层数对最内层套管内壁M ises应力分布规律的影响。套管−水泥环−地层多层组合系统对于保证最内层套管安全具有重要作用。

1 热固耦合作用下的多层组合系统力学模型

假设高温高压井套管−水泥环−地层多层组合系统无纵向变形，即不考虑垂向主应变的变化，此时套管−水泥环−地层多层组合系统可简化为平面应变问题。根据套管−水泥环−地层的实际服役条件，建立高温高压井套管−水泥环−地层多层组合系统热固耦合模型如图1所示(其中，hσ和Hσ分别为最小和最大非均匀地应力)。

在图1所示的热固耦合模型中，套管及水泥环为理想圆形、厚度均匀的各向同性材料。多层组合系统受到的载荷主要为非均匀地应力Hσ和hσ、套管内压p0、套管内温度T0与地层温度Tf的温差载荷。整个系统共包括n层，其中，第n层为地层，第n−1层为最外层的水泥环，第n−2层为最外层套管，以此类推。第i层的参数为内半径Ri−1、外半径Ri、弹性模量Ei、泊松比μi。

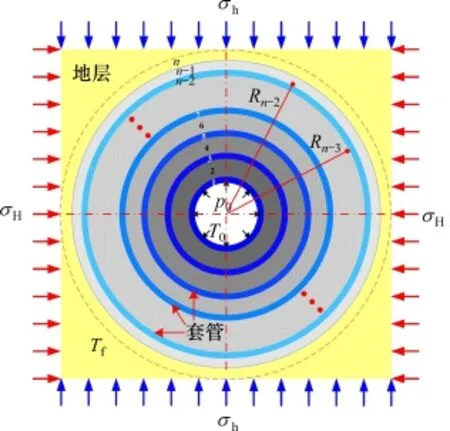
图1 多层组合系统热固耦合模型Fig.1 Thermo-structural coup ling analysismodel of multilayer composite system

2 热固耦合作用下的多层组合系统应力分析

2.1 边界应力分量的坐标变换

在图1所示的热固耦合模型中，需将直角坐标变换为极坐标进行应力求解。选取极坐标系下的模型外边界(r=Rn处)足够远，即不考虑外边界温度变化[9]。因此，由温度变化引起的内外边界热应力分量为0。利用坐标变化[10−11]，组合系统应力边界条件可描述为

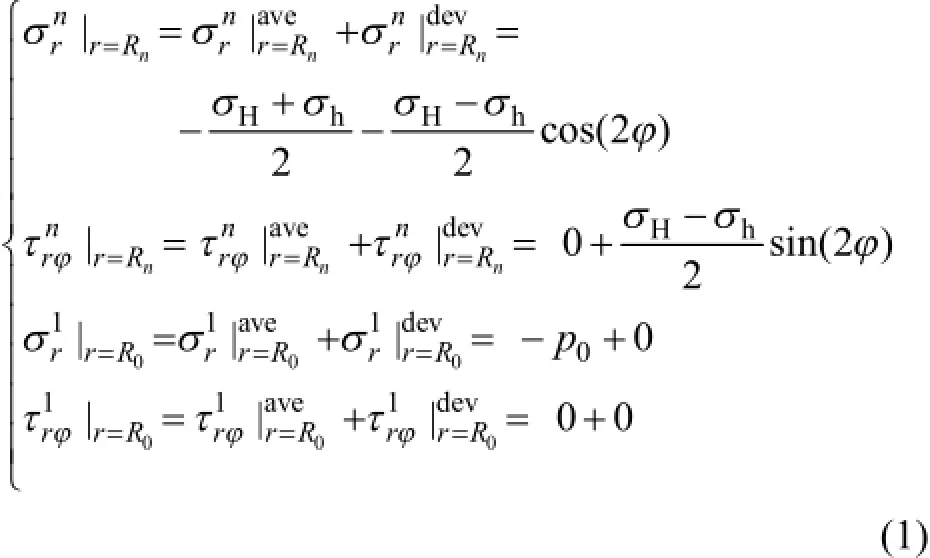
2.2 热固耦合分析

对于各向同性材料，稳态温度场及包含热力学耦合项的结构场控制方程为[12]

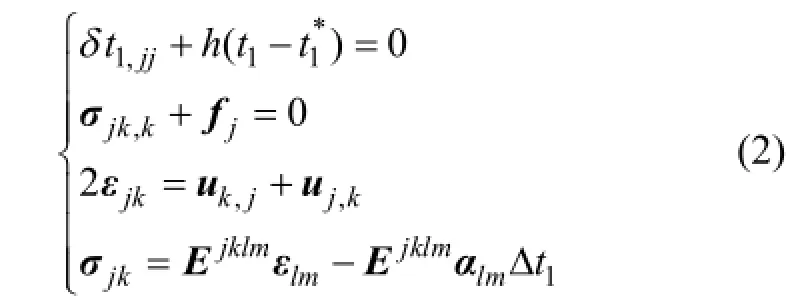
温度场边界条件为

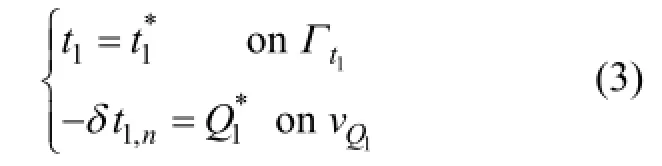
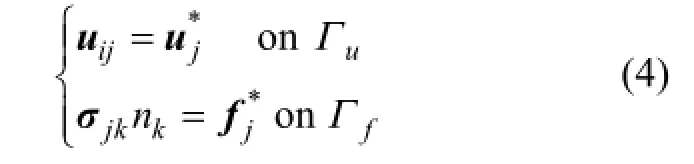
结构场边界条件为其中：δ为传导系数；h为对流换热系数；t1为温度；Δt1为变温；Γ为温度场区域边界；uj为位移向量；fj为体力分量；Ejklm为结构弹性模量张量；t1*为已知温度；Q*为边界已知热流量； u*为已知位移向量；f*为已

1

j

j知外力矢量；εkj，σjk和αjk分别为应变、应力和热膨胀系数张量；应力σjk为温度场t1的函数，下标j和k表示对坐标的微分；nk为面分量。

由式(2)中第4式可知，σjk由结构应力和温度应力线性叠加得到，因此，热固耦合问题中的应力分量可直接由平均应力场和偏差应力场引起的结构应力以及温度应力叠加得到。

2.3 平均应力场作用下的组合系统结构应力分析

由弹性力学可得组合系统中第i层圆环受均匀压力的拉梅解答[9]，其相对于外边界均匀压力的无因次表达式为

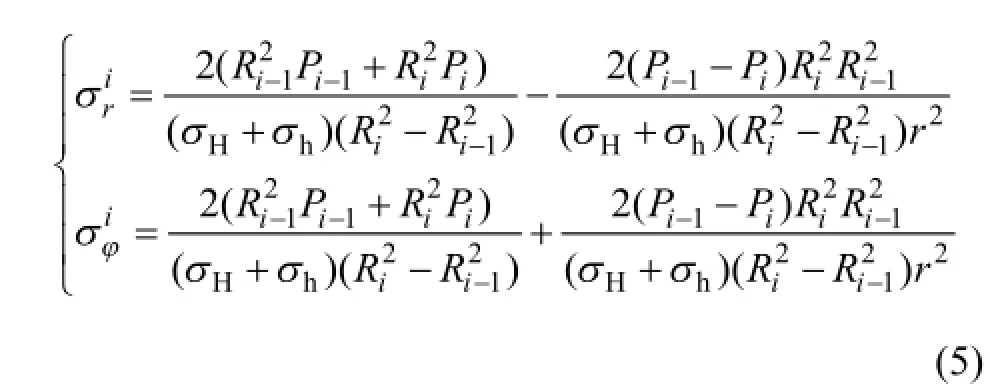
由极坐标几何方程和物理方程[9]，并结合均匀内外压作用下圆环环向位移为0的条件，可得第i层圆环径向位移的方程为

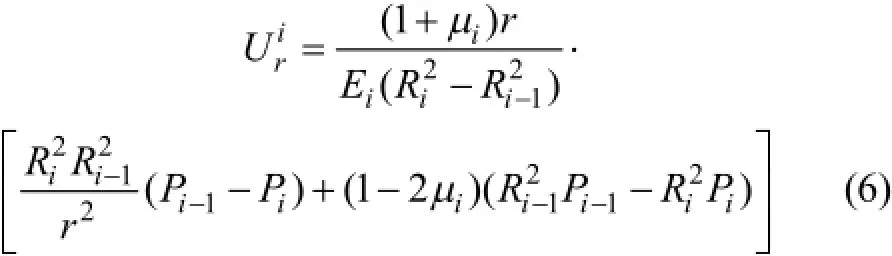
由多层组合系统接触面径向位移相等可得n−1个方程，形式如下：

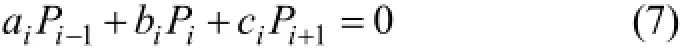
式中：系数ai，bi和ci为包含材料参数和几何尺寸的表达式；i=1,2,3,…,n−1。

2.4 偏差应力场作用下的组合系统结构应力分析

在偏差应力场作用下，通过应力函数求解得到组合系统第i层圆环相对于外边界非均匀应力的无因次表达式为

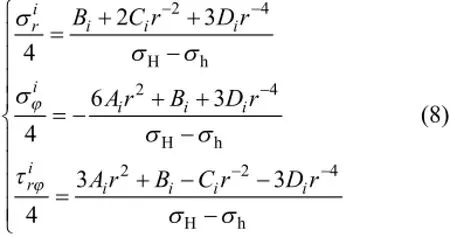
在式(8)～(10)中，共含有4n个未知量。为此，求解偏差应力场下的组合系统应力需建立4n个方程。利用偏差应力场边界条件及各层交界面的应力和位移连续性条件可组成4n个方程。

2.5 热载荷作用下的组合系统温度应力分析

2.5.1 温度场分析

工程上多数材料的热导率λ是温度的函数[13]，组合系统第i层圆环的热传导率可表示为λi=λ0i(1+eiθ)，进而可求得第i层圆环的线热流量qi：

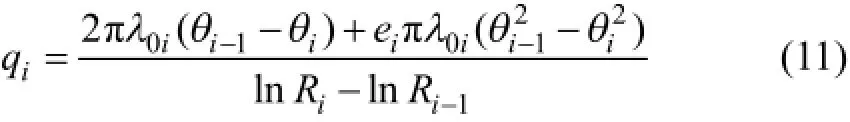
式中：θi−1为第i层圆环的内壁温度；θi为第i层圆环的外壁温度；λ0i为第i层圆环温度为0℃时材料热导率；ei为第i层圆环热导率随温度的变化梯度。

由能量守恒原理，可得求解组合系统稳定温度场的n−1个方程，形式为qi=qi+1(i=1,2,3,…,n−1)，利用试算法[14]可求得n−1个交界面的温度θi(i=1,2,3,…, n−1)，得到其温度场分布为

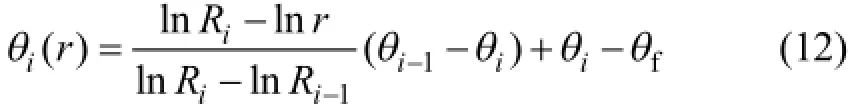
2.5.2 温度应力分析

通过求解满足平衡微分方程的位移势函数，获得相应于位移特解的应力分量。由满足相容条件的应力函数Φ=2−1·Fr2获得应力补充解σr=σφ=F，τrφ=0(F为常数)，最终求得第i层圆环的温度应力，其相对于内压p0的无因次表达式为

其中：Fi和Hi为第i层与力学参数有关的常数；iα为第i层材料的线胀系数；i=1,2,3,…,n。利用极坐标下的几何方程和物理方程，第i层圆环径向位移可表示为

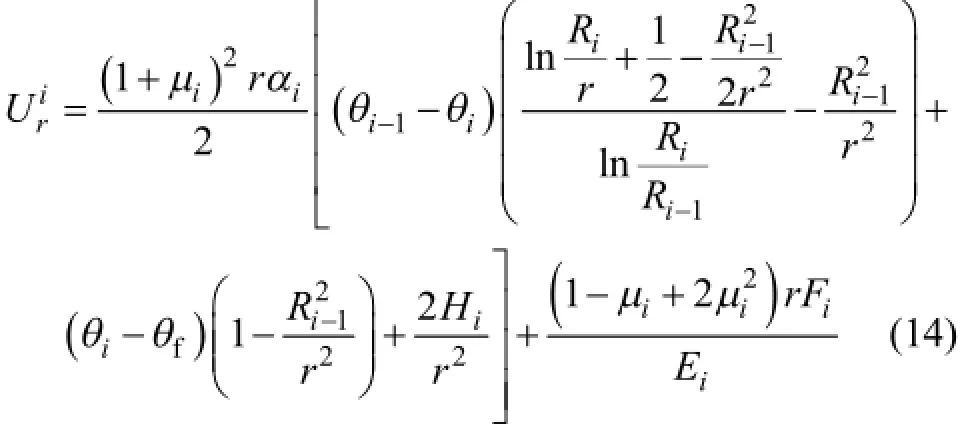
在式(13)和(14)中，共含有2n个未知量。为此，需建立2n个方程求解温度应力。利用温度场应力边界条件及各层交界面的应力和位移连续性条件可组成2n个方程。

3 算例分析

以新疆油田KS-XX井为例，该井地层压力系数高、地温梯度高、地层情况复杂，为此在2 800m段采用多层组合系统结构。各层管的几何尺寸、弹性模量、泊松比、线胀系数和热导率如表1所示，其中：最大水平主应力Hσ为70MPa、最小水平主应力σh为62MPa；最内层套管内径R0为64.95mm；内部压力p0为28MPa；套管温度T0为60℃；地层温度θf为340℃。

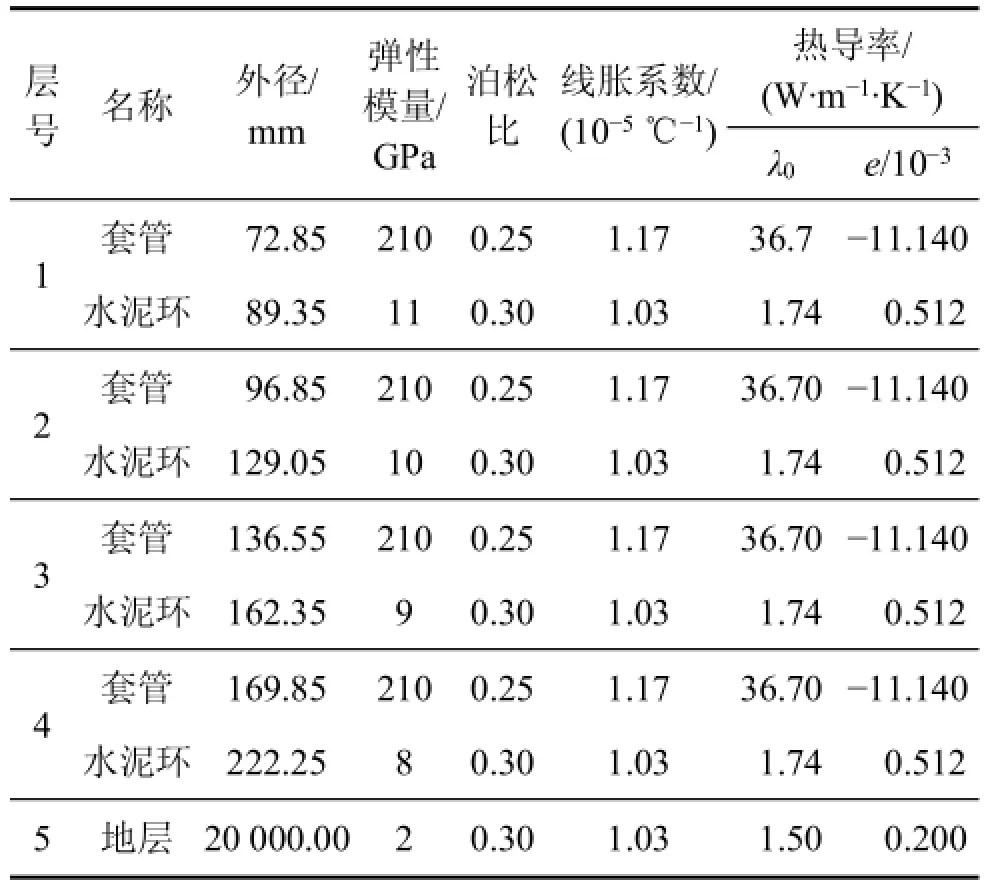
表1 计算参数Table1 Calculated parameters

3.1 高温高压井多层组合系统应力分析

利用本文推导的理论，编写程序并采用上述参数计算组合系统多层组合系统关键位置处的M ises应力，计算结果如图2所示。

由图2可知：在9层的套管−水泥环−地层多层组合系统中，套管内壁的M ises应力明显高于水泥环内壁的M ises应力，这与套管及水泥环的弹性模量相差较大密切相关。套管M ises应力的最大值与最小水平主应力hσ方向重合，最小值与最大水平主应力σH方向重合。套管M ises应力沿井周分布不均匀，呈现正弦曲线分布规律，这主要源自偏差应力场的作用。套管M ises应力的非均匀性在第1层和第4层套管内壁体现最明显，应力非均匀系数[8]分别高达1.678和1.569。对于第9层的套管−水泥环−地层组合系统，第4层套管是系统的最外层套管，直接受到非均匀地应力作用，这使得该层套管M ises应力非均匀性较强。

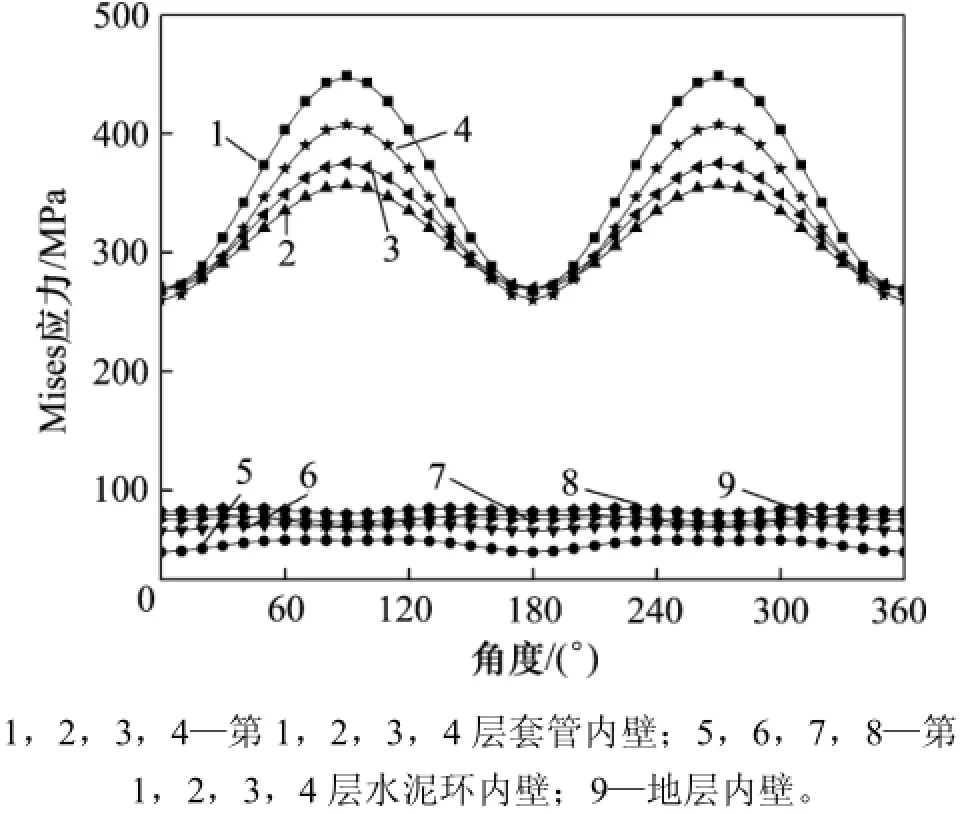
图2 多层组合系统各层内壁的M ises应力Fig.2 M ises stress distribution on inner facesofmultilayer com posite system model

对于第1层套管的内壁，直接面临临空面，其发生的应力集中必然使得该层套管M ises应力非均匀性最高。由于最内层套管的应力非均匀性较高，使得套管的抗外挤能力大大降低。在第2层和第3层套管内壁M ises应力非均匀性下降较多，应力非均匀系数分别为1.330和1.389。对于水泥环内壁的M ises应力，其应力非均匀性明显降低，这与其弹性模量明显低于套管的弹性模量直接相关。

根据图2所示结果，由于第1层、第4层套管的组合应力高于第2层、第3层套管，因此，各层套管应分别进行钢级选择。为了充分发挥套管管材的力学性质，第1层和第4层套管的钢级应高于第2层和第3层套管的钢级。以新疆油田KS-XX井为例，第1层和第4套管建议选择N80套管(最小屈服强度为552 MPa)，而第2层和第3层套管建议选择K55套管(最小屈服强度为379MPa)。

3.2 影响因素分析

根据以上分析结果，在套管−水泥环−地层组合系统中，最内层套管内壁的M ises应力最大，即最危险区域为最内层套管内壁。换句话说，只要最内层套管内壁的M ises应力小于许用应力，套管强度即满足。因此，为了保证套管安全，应重点关注最内层套管内壁的M ises应力。考虑到套管的弹性模量与泊松比基本不变，讨论水泥环厚度、弹性模量、泊松比、地层温度及套管及水泥环层数对最内层套管内壁M ises应力的影响。设套管壁厚为7.5mm，弹性模量为210 GPa，泊松比为0.25；水泥环壁厚为25mm，弹性模量为11GPa，泊松比为0.3；地层弹性模量2GPa，泊松比为0.3；地层温度为340℃，内壁温度为60℃。

3.2.1 水泥环厚度

保持其他参数不变，改变水泥环厚度，分析水泥环厚度对最内层套管内壁的M ises应力的影响。水泥环厚度变化范围为10～150mm。

图3 水泥环壁厚对最内层套管内壁M ises应力的影响Fig.3 Influenceof cement thicknesson Misesstress distribution of innermost casing insidewall

由图3可知：随着水泥环厚度的增加，最内层套管内壁的M ises应力增大，但增长趋势变小；当水泥环厚度从10mm增加到30mm时，最大M ises应力从417.237MPa增加到470.991MPa，增加53.754MPa，然而，当水泥环厚度从130mm增加到150mm时，最大M ises应力从656.744MPa增加到677.162MPa，增加20.418MPa；另外，随着水泥环厚度增加，最内层套管内壁M ises应力的非均匀性降低。当水泥环厚度为10mm时，非均匀系数为2.499 5，然而，当水泥环厚度增加到150 mm时，非均匀系数降低为1.389 3。

3.2.2 水泥环弹性模量

保持其他参数不变，改变水泥环弹性模量，分析水泥环弹性模量对最内层套管内壁的M ises应力的影响。水泥环弹性模量变化范围为10～80GPa。

由图4可知：随着水泥环弹性模量的增加，最内层套管内壁M ises应力呈现先增加后降低的趋势。在水泥环弹性模量达到30 GPa时，最内层套管内壁M ises应力达到极大值。当继续增大水泥环弹性模量，最内层套管内壁M ises降低。上述分析说明，对于多层组合系统，较低的水泥环弹性模量对于保护最内层套管安全是有益的。

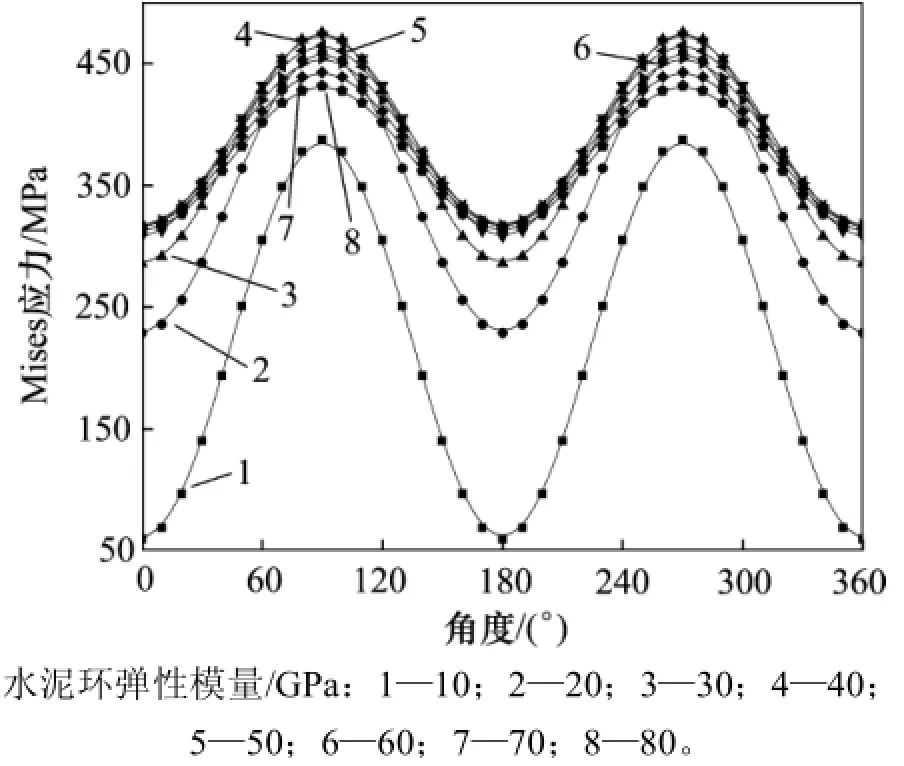
图4 水泥环弹性模量对最内层套管内壁Mises应力的影响Fig.4 Influence of cementelasticity moduluson M ises stress distribution of innermost casing insidew all

3.2.3 水泥环泊松比

保持其他参数不变，改变水泥环泊松比，分析水泥环泊松比对最内层套管内壁的M ises应力的影响。水泥环泊松比变化范围为0.1～0.4。

由图5可知：随着水泥环泊松比增大，最内层套管内壁M ises应力降低，但降低幅度较小；随着水泥环泊松比的变化，套管M ises应力的非均匀性变化不大。这说明水泥环泊松比的变化对最内层套管内壁M ises应力的影响较小。

3.2.4 地层温度

保持其他参数不变，改变地层温度，分析地层温度对最内层套管内壁的M ises应力的影响。地层温度变化范围为140～490℃。

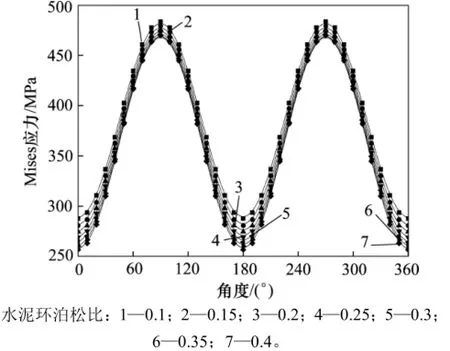
图5 水泥环泊松比对最内层套管内壁M ises应力的影响Fig.5 Influence of cement Poisson’s ratio on M ises stress distribution of innermost casing insidewall

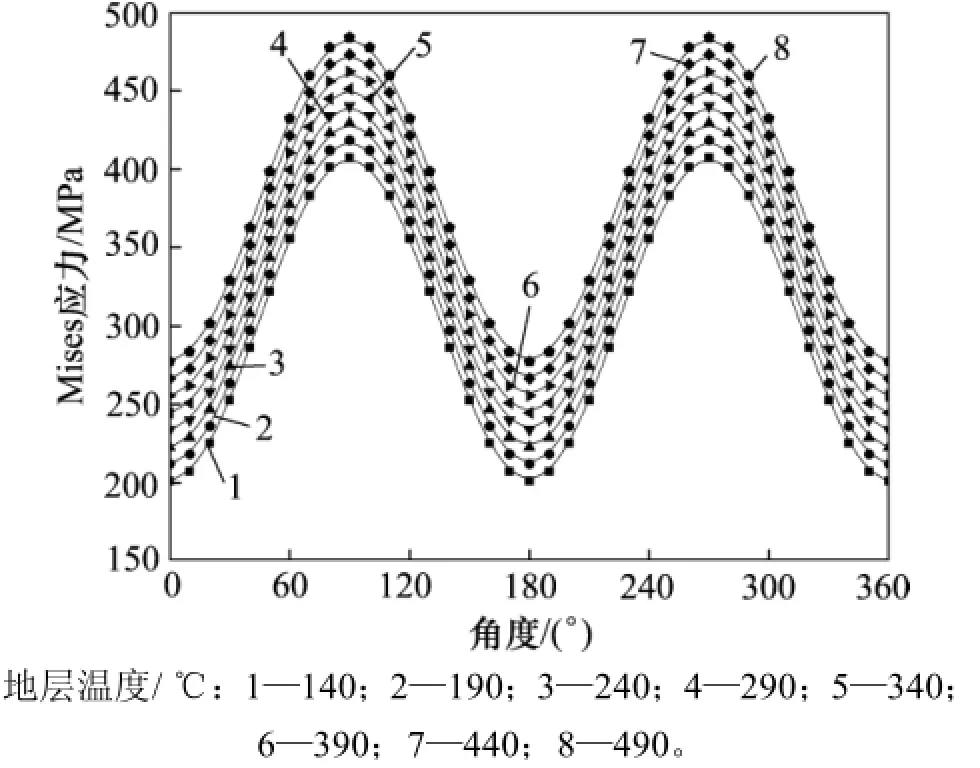
图6 地层温度对最内层套管内壁Mises应力的影响Fig.6 Influence of formation temperature on M ises stress distribution of innermost casing insidewall

由图6可知：随着地层温度增加，最内层套管内壁的M ises应力增大。由式(12)可知，距离套管中心相等的位置温度载荷相等，相应的温度应力相等。换句话说，对于距离套管中心相等的位置，温度应力是一个均匀应力场，这不会改变最内层套管内壁M ises应力沿井周的变化趋势，即M ises应力沿井周的变化趋势由非均匀地应力控制。

3.2.5 套管及水泥环层数

水泥环壁厚15mm，保持其他参数不变，改变套管及水泥环层数，分析套管及水泥环层数对最内层套管内壁的M ises应力的影响。套管层数变化范围为1～4。

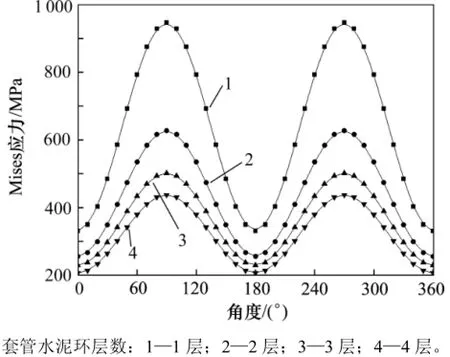
图7 套管层数对最内层套管内壁Mises应力的影响Fig.7 Influenceof casing layer numberon Mises stress distribution of innermost casing insidewall

由图7可知：随着多层组合系统层数增大，最内层套管内壁的M ises应力急剧减小。当套管−水泥环层数从1增加到4时，M ises应力最大值从947.207MPa降低到437.232MPa，降幅509.975MPa；非均匀应力系数从2.863减小到2.119。从以上分析可知，套管−水泥环−地层多层组合系统，对于降低最内层套管内壁的M ises应力及非均匀应力系数具有重要作用，具有工程应用的合理性。

4 结论

1)考虑热固耦合作用，建立了套管−水泥环−地层多层组合系统的力学模型，利用弹性力学理论获取了套管−水泥环−地层多层组合系统应力分布的解析解。该解析解表明，温度对套管−水泥环−地层多层组合系统的当量应力影响不能忽略。

2)水泥环厚度和地层温度的增加，最内层套管内壁的M ises应力增大；水泥环弹性模量的增加，最内层套管内壁M ises应力呈现先增大后减小的趋势；水泥环泊松比的变化对最内层套管内壁M ises应力的影响较小；多层组合系统层数增多，最内层套管内壁的M ises应力急剧减小。

3)在套管−水泥环−地层多层组合系统中，最内层套管和最外层套管的M ises应力比中间层的高。该系统对于降低最内层套管内壁的M ises应力、保证服役期间的套管安全具有重要工程价值。

[1]YIN Fei,GAO Deli.Mechanicalanalysisof casings in boreholes, under non uniform remote crustal stress fields:analytical& numerical methods[J].Computer M odeling in Engineering& Science,2012,89(1):25−37.

[2]殷有泉,陈朝伟,李平恩.套管−水泥环−地层应力分布的理论解[J].力学学报,2006,38(6):835−842.

YIN Youquan,CHEN Zhaowei,LIPingen.Theoretical solutions of stress distribution in casing-cement and stratum system[J]. Chinese Journal of Theoretical and Applied Mechanics,2006, 38(6):835−842

[3]房军,岳伯谦,赵怀文,等.非均匀地应力作用下套管和水泥环表面受力特性分析[J].石油大学学报(自然科学版),1997, 21(1):46−48.

FANG Jun,YUE Boqian,ZHAO Huaiwen,et al.Analysis of surface loading on casing and cement sheath under non uniform geologic stress[J].Journal of China University of Petroleum (NaturalScience Edition),1997,21(1):46−48

[4]房军,赵怀文,岳伯谦,等.非均匀地应力作用下套管与水泥环的受力分析[J].石油大学学报(自然科学版),1995,19(6): 52−57.

FANG Jun,ZHAN Huaiwen,YUE Boqian,et al.Analysis of sheath loading property of casing and cement under non uniform geologic stress[J].Journal of China University of Petroleum (NaturalScience Edition),1995,19(6):52−57

[5]房军,谷玉洪,米丰珍.非均匀载荷作用下套管挤压失效数值分析[J].石油机械,1999,27(7):34−37.

FANG Jun,GU Yuhong,M IFengzhen.A numerical analysis of casing collapse under non uniform load[J].China Petroleum Machinery,1999,27(7):34−37.

[6]LAST N C,MUJICA M,PATTILLO P D,et al.Evaluation, impact,and management of casing deformation caused by tectonic forces in Andean Foothills,Colombia[J].SPE Drill Complet,2006,21(2):116−124.

[7]李军,陈勉,张辉.定向井套管应力随地应力条件的变化规律研究[J].石油学报,2005,26(1):109−112.

LI Jun,CHEN M ian,ZHANG Hui.Study on varying rules of casing stress in directional hole w ith in-situ stress conditions[J]. Acta Petrolei Sinica,2005,26(1):109−112.

[8]王宴滨,高德利,房军.套管−水泥环−地层多层组合系统受力特性分析[J].应用力学学报,2014,31(3):387−393.

WANG Yanbin,GAO Deli,FANG Jun.Mechanical characteristics analysis of casing-cement ring-formation multilayer composite system[J].Chinese Journal of Applied Mechanics,2014,31(3):387−393.

[9]徐芝纶.弹性力学(上册)[M].北京:人民教育出版社,1978: 60−77.

XU Zhilun.Elastic mechanics(volume1)[M].Beijing:People’s Education Press,1978:60−77.

[10]杨桂通.弹塑性力学引论[M].北京:清华大学出版社,2004: 115−124.

YANGGuitong.Induction to elasticity and plasticity[M].Beijing: Tsinghua University Press,2004:115−124.

[11]李志明,殷有泉.油水井套管外挤力计算及其力学基础[M].北京:石油工业出版社,2006:5−38.

LIZhiming,YIN Youquan.Oil and water wells outside casing extrusion force calculation and mechanical foundation[M]. Beijing:Petroleum Industry Press,2006:5−38.

[12]左孔天,钱勤,赵雨东,等.热固耦合结构的拓扑优化设计研究[J].固体力学学报,2005,26(4):447−452.

ZUO Kongtian,QIAN Qin,ZHAO Yudong,et al.Research on the topology optim ization about thermo-structural coup ling field[J].Chinese Journal of Solid M echanics,2005,26(4): 447−452.

[13]戴锅生.传热学[M].北京:高等教育出版社,1999:31−35.

DAI Guosheng.Heat transfer[M].Beijing:Higher Education Press,1999:31−35.

[14]陈艳华,张振迎,景宝国.试算法在多维非稳态导热问题中的应用[J].建筑节能,2010,227(38):68−71.

CHEN Yanhua,ZHANG Zhenying,JING Baoguo.Trial algorithm applied on multi-dimensional transient heat conduction[J].Building Energy Efficiency,2010,227(38): 68−71.

(编辑 赵俊)

M echanical characteristicsanalysisof casing−cement sheath−formationmultilayer com posite system w ith thermo-structural coup ling effects

ZHAO Xinbo1,2,HAN Shengchao1,YANG Xiujuan1,YAN Xiangzhen1,3,ZHANG Lisong1

(1.College of Pipelineand Civil Engineering,China University of Petroleum(EastChina),Qingdao 266580,China; 2.College of Science,Qingdao Technology University,Qingdao 266033,China; 3.Oiland Gas CAE Technology Research Center,China University of Petroleum(EastChina),Qingdao 266580,China)

According to elastic mechanics,analytical solution of the equations under the action of thermo-structural coupling wasobtained by considering contact,continuity and boundary conditions in themultilayer com posite system of casing−cement sheath−formation in HPHT production well.The multilayer composite system was subjected to non-uniform in-situ stress,uniform inner pressure and tem perature pressure.The influences of cement thickness,cement elastic modulus,cement Poisson’s ratio,formation temperature and layer number of casing−cement sheath on M ises stress distribution of the insidewall of innermost layer casingwere discussed.The results show thatall the above factors have great influences on the M ises stress distribution.Comparing monolayer and multilayer casing−cement sheath−formation system of casing−cement sheath−formation,the M ises stress distribution of the inside wall of innermost layer casing inmultilayer casing−cementsheath−formation system is distinctly decreased,and so themultilayer casing−cement sheath−formation system hasan importantengineering value to ensure the safety of casing strength during service.

casing−cementsheath−formation;thermo-structural coupling;multilayer com positesystem;elasticmechanics

TE329

A

1672−7207(2017)03−0837−07

10.11817/j.issn.1672-7207.2017.03.035

2016−03−06；

2016−05−30

国家自然科学基金资助项目(51274231，51374228)；国家自然科学基金−石化联合基金资助项目(U1262208)；中国石油天然气集团公司重点实验室课题资助项目(2014A-4214)；青岛市应用基础研究计划项目(15-9-1-71-jch)(Projects(51274231,51374228) supported by the National Natural Science Foundation of China;Project(U1262208)supported by the National Science Foundation of China and Petrochem ical Foundation;Project(2014A-4214)supported by the Key Laboratory of China National Petroleum Corporation;Project (15-9-1-71-jch)supported by the Applied Basic Research Program of Qingdao City)

赵新波，博士，讲师，从事油气田地下工程力学研究；E-mail:zxbups@163.com