不同干密度下非饱和土土−水特征曲线

陈宇龙，内村太郎

不同干密度下非饱和土土−水特征曲线

陈宇龙，内村太郎

(东京大学土木工程系，日本东京，113-8656)

对吸湿与脱湿过程中引起非饱和土土−水特征曲线进行分析，观察不同密度土样的土−水特征曲线与滞后现象。利用Fred lund and Xing的土−水特征曲线模型对试验数据进行拟合，得到模型拟合参数与土−水特征曲线参数的定量关系。研究结果表明：进气值随着参数a的增大而线性增大，残余基质吸力随着参数m的增大而呈幂函数减小，减湿率随着参数n的增大而呈指数减小。干密度对土−水特征曲线有显著影响。随着干密度增大，残余基质吸力与进气值及进水值增大，减湿率减小，滞后现象的显著程度降低。瓶颈效应、不同的接触角和空气体积是造成滞后效应的主要因素。

非饱和土；土−水特征曲线；干密度；滞后现象

土−水特征曲线(soil-water characteristic curve，SWCC)是描述非饱和土中吸力与饱和度或体积含水率之间关系的曲线[1−2]，它能够反映非饱和土的众多性质如渗透性、强度、应变、应力状态等[3−6]。同时，作为解释非饱和土行为的一项基本本构关系，土−水特征曲线是将理论、试验及预测方法有机结合的重要关系之一[7−8]，也是构筑非饱和土各种重要关系的基础。因此，通过土−水特征曲线研究非饱和土的相关性质具有重要的意义。目前已有学者给出了一系列更高效更经济的建立土−水特征曲线的方法。FREDLUND等[9]在考虑孔隙孔径影响基础上建立了土−水特征曲线的理论基础。GUPTA等[10−11]利用砂土、粉土与黏土的含量及堆积密度的统计规律预测了土−水特征曲线。以上研究较少涉及滞后效应的定量关系与拟合参数。脱湿曲线高于吸湿曲线，两者形成滞回圈，故研究具体的工程问题时，忽略滞后性质影响必然导致一定的误差。鉴于此，有必要进一步定量研究土−水特征曲线的预测方法。为此，本文作者拟通过自行研制组装的仪器对非饱和土吸湿与脱湿过程的土−水特征曲线进行研究，分析曲线与Fredlund和Xing模型[12]的拟合参数的定量关系以及不同干密度下的土−水特征曲线与滞后现象。

1 试验概况

1号土样取自某自然边坡，2号土样取自铁路路堤。土样的物理力学指标如表1所示。根据规范[13]可知，2类土均为粉质砂土。试样采用直径×长度为50 mm×60mm的圆柱体土样。1号土样的干密度选取1.22，1.35和1.50 g/cm3，2号土样的干密度选取1.25，1.35和1.42 g/cm3。土样颗粒分布曲线见图1，试验仪器见图2。空气由仪器上部通过电脑控制注入。底座为进气值300 kPa的圆盘形陶土板，底部与导管相连，水能够从导管进出。导管另一端连接透明容器，容器上部开了1个小孔，与大气相通，使得土样中的孔隙水压为0 kPa。为修正水分蒸发造成的误差，在容器旁放置1个与试样所用容器完全相同的容器，加入等质量的水，从而可知在相同的环境下蒸发的水的质量。

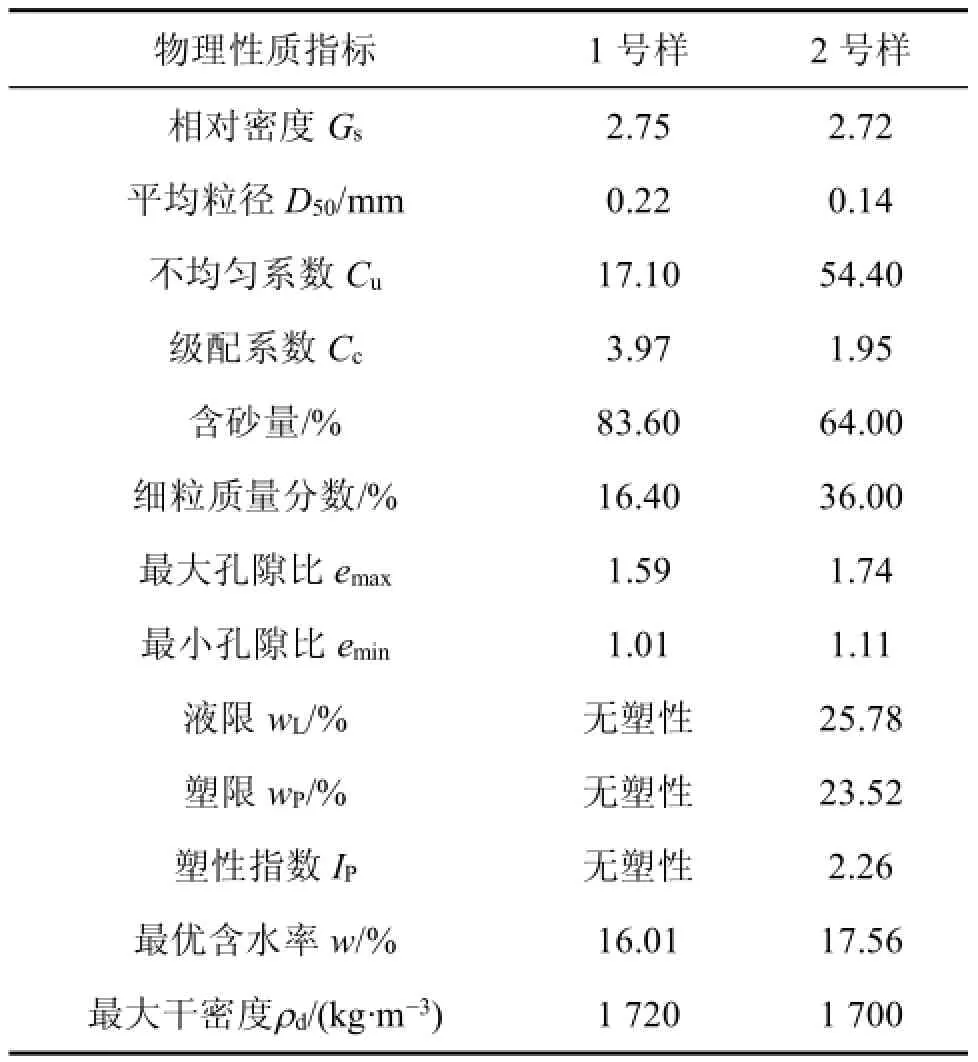
表1 土的物理力学性质指标Table1 Physico-mechanicalpropertiesof soil

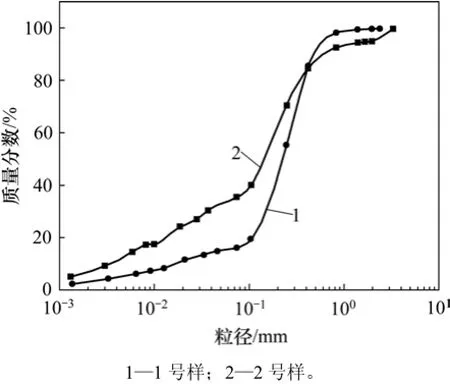
图1 颗粒分布曲线Fig.1 Grain size distribution curves for testmaterials

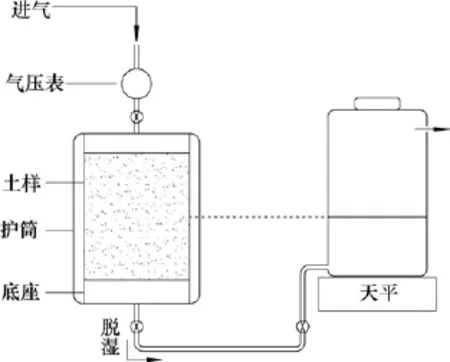
图2 试验仪器Fig.2 Instrument for experiment

建立土−水特征曲线最重要的是测定基质吸力和含水率。试验的具体操作步骤如下：首先对底座进行饱和，并按照文献[14]中的方法检查饱和状态是否良好；饱和之后，将底座与容器相连，保持饱和状态；将橡皮膜套上底座，安装护筒，使橡皮膜贴住护筒内壁；关闭下部的导管，取烘干后的土样按含水率10%调制均匀后分层装入护筒，压密至预定厚度以控制其干密度；打开下部的导管，使容器中的水位高于土样使其饱和，此过程往往需要48 h以上；安装顶盖，使容器的水位与试样的中部平行；待容器与水的质量稳定后，记录初始质量，即吸力为0 kPa时的读数；依次升高气压(气压等于吸力)至0.5，1.0，2.0，3.0，4.0，5.0，6.0，7.0，8.0，10.0，15.0，20.0，30.0，50.0，100.0和200.0 kPa；当天平的读数恒定后读取数值。以上为脱湿的过程，脱湿之后再进行吸湿过程，即将气压逐次降至0 kPa；水会逐渐流入土样，待平衡后读取数据；吸湿过程结束后，将土样取出烘干，测得含水率，用于反算和修正之前测得的含水率。

2 试验结果及分析

本文选用Fredlund和Xing模型[12]对试验数据进行拟合。Fredlund和Xing模型的表达式为：

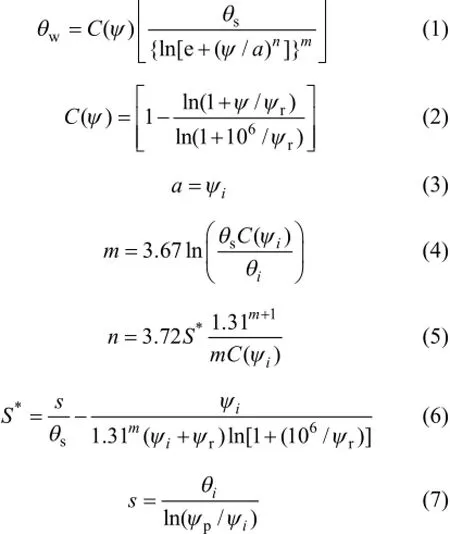
式中：wθ为体积含水率；sθ为饱和体积含水率；rθ为残余体积含水率；s为减湿率；ψ为基质吸力(kPa)；rψ为残余基质吸力(kPa)；a为进气值的相关参数(kPa)；n为减湿率的相关参数；m为残余含水率的相关参数，如图3所示[15]。残余基质吸力、进气值、减湿率以及拟合参数(a,m,n)均由分析软件SoilVision确定。

饱和土体在脱湿过程中，吸力梯度减小，大孔隙中的水分流失，当达到ψi点之后，吸力梯度增加，小孔隙中的水分才开始流出，ψi点正是大、小孔隙水分变化难易的转化点。

图3 土−水特征曲线与拟合参数示意图[15]Fig.3 Schematic diagram of SWCCsand fitting parameters[15]

表2所示为通过拟合得到的参数，图4和图5所示为2种土样在不同干密度条件下的土−水特征曲线。陶土板的进气值较小，进气值大于200 kPa的部分是按照Fredlund-Xing模型向外延伸的。从图4和5可以看出土−水特征曲线呈现典型的3阶段变化特征：边界效应阶段、转化阶段和残余阶段。

处于边界效应阶段，基质吸力从无到有，土体孔隙呈现出水连续孔隙结构特征。对于转化阶段，基质吸力增大，土体孔隙从水连续转化为气连续，基质吸力在对土体的吸持作用越来越显著；在残余阶段，基质吸力非常大，孔隙状态完全到达气连续、水不连续。

分别对比分析不同干密度下的土−水特征曲线可以看出，受干密度的影响，土−水特征曲线的形态随之改变。进气值ψa、残余基质吸力ψr与减湿率s控制土−水特征曲线的形状。

参数变化曲线如图6所示。由图6可以看出：2种土样的土−水特征曲线参数与模型参数的对应关系近乎一致；进气值随着参数a的增大而呈线性增大；残余基质吸力随着参数m的增大而呈幂函数减小，减湿率随着参数n的增大而呈指数减小。

参数a和n越大，水入渗后，边坡的安全系数越低，且降低速度越快；参数m越小，水入渗后，边坡的安全系数越低，且降低速度越快。参数(a,m,n)对于排水性良好的边坡影响较小，对排水性较差的边坡有显著影响[16]。

基质吸力与水的表面张力服从毛细作用[17]：

式中：ua为孔隙气压；uw为孔隙水压；Ts为水的表面张力；Rs为弯液面的曲率半径。土体含水率降低时，孔隙气体增多，毛细管增多，毛细效应增强，基质吸力增大。

土样微观结构图如图7所示。从图7可以看出：处于非饱和状态的土体内部会产生许多弯液面。基质吸力就是通过这些弯液面影响着土体强度：随着含水率降低，土体由最初的饱和状态向非饱和状态转化，在土液气三相共存的体系内，孔隙气体含量增加，气泡膨胀扩大并与颗粒表面搭接，粒间弯液面开始出现并相互独立。此时，弯液面内的孔隙水压和水体外的孔隙气压之间压力差形成基质吸力(ua−uw)并逐渐升高。弯液面上的表面张力的反作用力作用在土颗粒上，对其产生压应力，从而增大了土体的凝聚力。

表2 拟合参数Table2 Fitting parameters

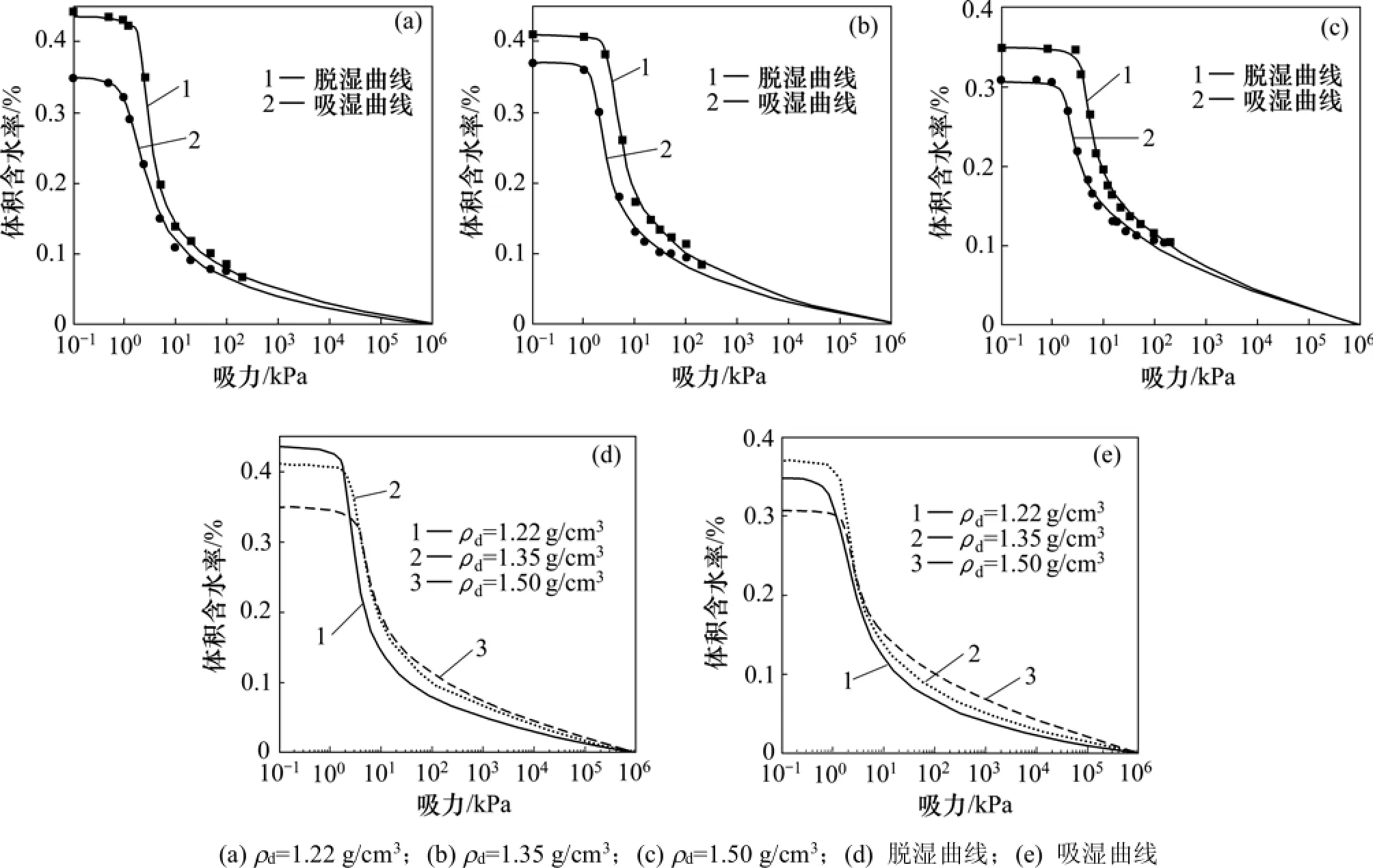
图4 1号土样土−水特征曲线Fig.4 Soil−water characteristic curvesof sam ple 1

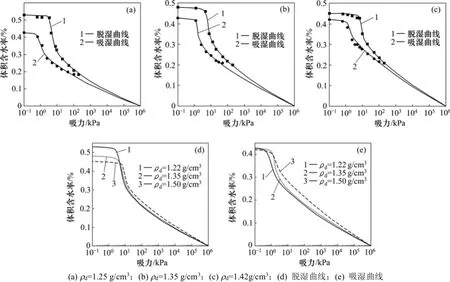
图5 2号土样土−水特征曲线Fig.5 Soil−water characteristic curvesof sample2

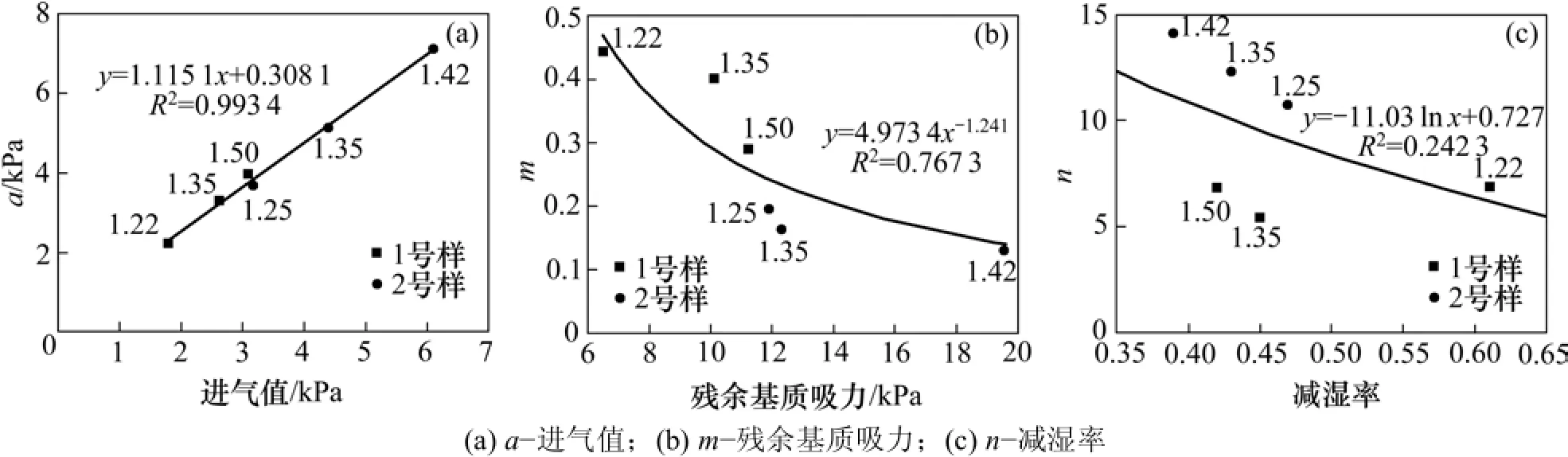
图6 参数变化曲线Fig.6 Curves for fitting parameters

由图4(d)和4(e)以及图5(d)和5(e)可知：残余基质吸力、进气值及进水值随着干密度的增大而增大，饱和体积含水率与减湿率随着干密度的增大而减小。干密度与进气值、残余基质吸力及减湿率的关系曲线见图8。从图8可见：2种土样的土−水特征曲线参数随干密度的变化规律几乎一致。1号土样的土−水特征曲线参数的变化幅度逐渐减小，而2号土样的土−水特征曲线参数的变化幅度递增；随着干密度的增加，1号土样的进气值增加了73%，残余基质吸力增加了72%，减湿率减小了31%；而2号土样的进气值增加了92%，残余基质吸力增加了64%，减湿率减小了17%。

图7 土样微观结构图Fig.7 Microcosm ic structure of soilsamples

在土体材料一定时，土体的脱湿状态及对应的基质吸力只取决于土体中孔隙的孔径和数量，即在一定的基质吸力条件下，小于该等效孔隙孔径的孔隙中充满水，大于此孔隙孔径的孔隙则失水，因此，土−水特征曲线在反映土体基质吸力与含水率关系的同时，也反映了土中的孔隙状态[18]。干密度对土−水特征曲线的影响是通过改变土体孔隙状况来表现的，干密度越大，土颗粒就越紧密，孔隙孔径和数量越小，饱和体积含水率越低，且渗透性越差，表现出较好的持水能力，空气难以进入土体，土体无论是排水还是吸水都比较困难，使进气值、进水值得以提高。超过进气值后，较大干密度作用下曲线斜率较缓和，土样排水较慢，导致相同基质吸力时，较大干密度土样的体积含水率高于较小干密度土样的体积含水率，且体积含水率相同时，弯液面的曲率半径越小及基质吸力越大，残余基质也越大。

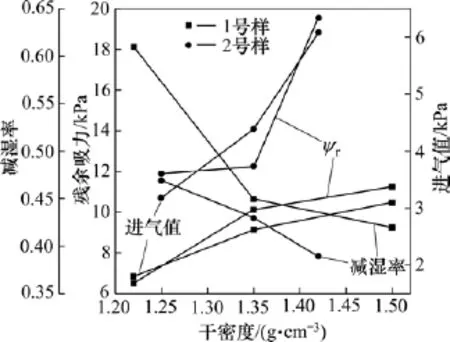
图8 干密度与进气值、残余基质吸力及减湿率的关系曲线Fig.8 Variation of dry density with air-entry value,residual suction and slopeof SWCC

滞后效应的存在使得对应于一相同的基质吸力，土体的体积含水率不唯一。造成滞后的原因主要有[19−21]：孔隙孔径的不均匀分布、瓶颈效应、吸湿和脱湿过程中接触角不同、吸湿和脱湿过程中带入的空气体积不同、吸湿和脱湿过程中膨胀和收缩引起的土结构的改变不同、土的老化效应等。瓶颈效应、不同的接触角和空气体积是主要因素，而膨胀和收缩及老化效应的影响较小。因为土体在试验过程中受护筒限制，体积不会改变，而且试验历时较短，不会发生老化效应。

脱湿与吸湿曲线包围的面积定义为滞后现象的显著程度H：

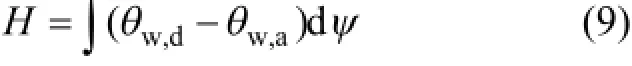
式中：w,dθ和w,aθ分别为吸湿过程和脱湿过程的体积含水率。

积分范围为基质吸力(0.1,106)。2种土样在不同干密度下的滞后现象的计算结果见图9。从图9可见：随着干密度的增加，更小的孔隙与更显著的毛细作用导致滞后现象的显著程度降低。

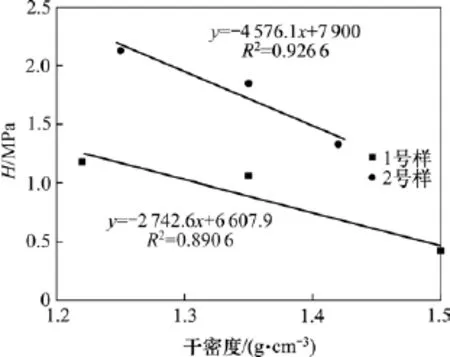
图9 滞后程度与干密度的关系曲线Fig.9 Variation of dry density with hysteresis

1号土样和2号土样在土−水特征曲线上的差异在于细粒含量的不同。细粒含量越高，小孔的数量越多，同一体积含水率下对应的基质吸力越大[22]。RAO等[23]发现：黏粒含量越大，土中基质吸力越大，浸湿越容易塌陷。

3 结论

1)进气值随着参数a的增大而呈线性增大，残余基质吸力随着参数m的增大而呈幂函数减小，减湿率随着参数n的增大而呈指数减小。

2)干密度对土−水特征曲线有显著影响。残余基质吸力与进气值及进水值随着干密度的增大而增大，减湿率随着干密度的增大而减小。随着干密度增加，滞后现象的显著程度降低，其中，瓶颈效应、不同的接触角和空气体积是主要因素，而膨胀和收缩及老化效应的影响较小。

[1]MALAYA C,SREEDEEP S.Critical review on the parameters influencing soil-water characteristic curve[J].Journal of Irrigation&Drainage Engineering,2012,138(1):55−62.

[2]MA Tiantian,WEIChangfu,WEIHouzhen,etal.Hydraulic and mechanical behavior of unsaturated silt:experimental and theoretical characterization[J].International Journal of Geomechanics,2015,16(6):D4015007-1−13.

[3]DASTJERDI M T.Effect of confining stress on soil water retention curve and its impact on the shear strength of unsaturated soils[J].Vadose Zone Journal,2014,13(5):1−11.

[4]GALLAGE C,UCHIMURA T.Direct shear testing on unsaturated silty soils to investigate the effects of drying and wetting on shear strength parameters at low suction[J].Journalof Geotechnical&Geoenvironmental Engineering,2016,142(3): 04015081-1−9.

[5]PRIONO,RAHARDJO H,CHATTERJEA K,et al.Effect of hydraulic anisotropy on soil–water characteristic curve[J].Soils and Foundations,2016,56(2):228−239.

[6]RAHIM IA,RAHARDJO H,LEONG E C.Effects of soil–water characteristic curve and relative permeability equations on estimation of unsaturated permeability function[J].Soils& Foundations,2015,55(6):1400−1411.

[7]BARBOUR L.Nineteenth Canadian geotechnical colloquium: the soil-water characteristic curve:a historic perspective[J]. Canadian Geotechnical Journal,1998,35(5):873−894.

[8]LEONG E C,RAHARDJO H.Review of soil-water characteristic curve equations[J].Journal of Geotechnical and Geoenvironmental Engineering,1997,123(12):1106−1117.

[9]FREDLUND M D,WILSON G W,FREDLUND D G. Prediction of soil-water characteristic curve from the grain-size distribution curve[C]//Proceedings of the 3rd Symposium on Unsaturated Soil.Rio de Janeiro,Brazil,1997:13–23.

[10]GUPTA S C,LARSON W E.Estimating soil water retention characteristics from particle size distribution,organic matter percent,and bulk density[J].Water Resources Research,1979, 15(6):1633−1635.

[11]ARYA L M,PARIS JF.A physicoempiricalmodel to predict the soil moisture characteristic from particle-size distribution and bulk density data[J].Soil Science Society of America Journal, 1981,45:1023−1030.

[12]FREDLUND D G,XING A.Equations for the soil-water characteristic curve[J].Canadian Geotechnical Journal,1994, 31(4):521−532.

[13]ASTM Standard D2487,Standard practice for classification of soils for engineering purpose(USCS)[S].

[14]HUANG Y.Effects of suction on strength and deformation behavior of unsaturated collapsible soils[D].Tokyo:University of Tokyo.Departmentof CivilEngineering,1994:12−32

[15]TOAN D T,KOM INE H,MURAKAMIS,etal.Grain size and soil suction effect on hydraulic conductivity and shear strength of simulated red river soil[J/OL].Advances in Geotechnical Infrastructure,2013,doi:10.3850/978-981-07-4948-4_162.

[16]RAH IM IA,RAHARDJO H,LEONG E C.Effect of hydraulic properties of soil on rainfall-induced slope failure[J]. Engineering Geology,2010,114:135−143.

[17]GHANIM A H.Shear deformation of unsaturated soil in slope under constant stresses and wetting/drying conditions[D].Tokyo: University of Tokyo.Department of Civil Engineering,2014: 5−12.

[18]SILLERS W S,FREDLUND D G,ZAKERZADEH N. Mathematical attributes of some soil-water characteristic curve models[J].Geotechnical and Geological Engineering,2001(19): 243−283.

[19]陈宇龙,内村太郎.粒径对土持水性能的影响[J].岩石力学与工程学报,2016,35(7):1474−1482. CHEN Yulong,UCHIMURA Taro.Influence of particle size on water retention of soils[J].Chinese Journal of Rock Mechanics and Engineering,2016,35(7):1474−1482.

[20]MAQSOUD A,MBONIMPA M.Predicting hysteresis of the water retention curve from basic properties of granular soils[J]. Geotechnical and Geological Engineering,2012,30(5): 1147−1159.

[21]GALLAGE C,KODIKARA J,UCHIMURA T.Laboratory measurement of hydraulic conductivity functions of two unsaturated sandy soils during drying and wetting processes[J]. Soils&Foundations,2013,53(3):417−430.

[22]GALLAGE C P K,UCHIMURA T.Effects of dry density and grain size distribution on soil-water characteristic curves of sandy soils[J].Soilsand Foundations,2010,50(1):161−172.

[23]RAO SM,REVANASIDDAPPA K.Role of soil structure and matric suction in collapse of a compacted clay soil[J]. Geotechnical Testing Journal,2003,26(1):102−110.

(编辑 赵俊)

Soil-water characteristic curve for unsaturated soilat different dry densities

CHEN Yulong,UCHIMURA Taro

(Departmentof Civil Engineering,the University of Tokyo,Tokyo 113-8656,Japan)

Drying and wetting soil-water characteristic curves(SWCCs)for two sandy soilswere investigated to research the effects of dry density on the SWCCs and hysteretic behaviors.Drying and w etting SWCCs were obtained for tw o sandy soils w ith different dry densities.The test data were best-fitted using the Fred lund and X ing equation.The results show that the fitting parameter a increases linearly with the increase of the air-entry value of the SWCC,the fitting parameter m decreaseswith the increase of the residual suction of the SWCC and the fitting parameter n also decreases w ith the increase of the slope of the SWCC.W ith the increase of parameter a,the air-entry value increases linearly;w ith the increase of parameter m,the residual suction decreases in power function,and w ith the increase of parameter n, the slope of drying SWCC decreases in exponential function.The dry density has significant effects on the soil-water characteristic curve.W ith the increase of dry density,the residual suction,air-entry value and water-entry value increase, and both the slope of drying SWCC and the hysteresis decrease.The hysteresis ismainly attributed to the ink-bottle effect, the contactangle effectand entrapped air.

unsaturated soil;soil-water characteristic curve;dry density;hysteresis

TU441

A

1672−7207(2017)03−0813−07

10.11817/j.issn.1672-7207.2017.03.032

2015−03−06；

2015−06−10

国家自然科学基金资助项目(10772205)(Project(10772205)supported by the National Natural Science Foundation of China)通信作者：陈宇龙，博士，研究员，从事岩土工程的研究；E-mail:673054399@qq.com