A Construction of Quantum Error-Locating Codes∗

Ji-Hao Fan(樊继豪)and Han-Wu Chen(陈汉武),2,†School of Computer Science and Engineering,Southeast University,Nanjing 289,China

2Key Laboratory of Computer Network and Information Integration(Southeast University),Ministry of Education,Nanjing 211189,China

1 Introduction

Quantum information is sensitive and vulnerable to quantum nosie caused by decoherence.Quantum errordetecting and quantum error-correcting techniques are needed to enable reliable quantum computation and quantum communication.Utilizing redundancy,quantum error-correcting codes(QECC)are used to detect and correct quantum errors that may have occurred during the quantum information processing.It is possible to construct QECCs from classical error-correcting codes that satisfy certain conditions.[1−2]Quantum stabilizer codes[3−5]provide a general framework to construct QECCs analogous to classical additive codes.Many works have been done in the construction of QECCs,e.g.,quantum Hamming codes,[6]quantum cyclic codes,[7−8]quantum MDS codes,[9−10]quantum concatenated codes[11]and other types of quantum codes.[12]

In Ref.[13],Wolf and Elspas introduced a special class of error control codes called error-locating(EL)codes,which lies midway between error-correcting codes and error-detecting codes.The whole codeword of EL codes can be regarded as being divided into several sub-blocks that are mutually exclusive from each other.EL codes can indicate which one sub-block is in error,but do not need to permit the exact location of the erroneous symbol positions within each sub-block.EL codes were originally proposed to be used in a decision feedback communication system,and can also be used in computer memory systems.[14]Then in Ref.[15],a more comprehensive class of codes called generalized error-locating(GEL)codes were proposed.Furthermore,it was shown that GEL codes are equivalent to generalized concatenated codes.[16]

In this study,we propose a quantum analog of classical error-locating codes.The original error-locating codes were constructed based on cyclic codes with generator polynomials g(x)over F2in Ref.[13].We show that,for an e-EL code derived from an arbitrary binary cyclic code,the resultant e-EL code is a dual-containing code only if g(x)does not contain the(1+x)-factor.Therefore,we can construct the corresponding quantum error-locating codes based on dual-containing EL codes,and thus quantum error-locating codes have similar quantum error-locating properties as their classical counterparts.

The rest of the paper is organized as follows.In Sec.2,we give a brief introduction of classical EL codes and quantum error-correcting codes.In Sec.3,we present the construction of quantum error-locating codes from classical EL codes.The conclusion and discussion are given in Sec.4.

2 Preliminaries

In this section,we review the concept of classical EL codes and some basic facts about QECCs,for the details on EL codes and QECCs,please refer to Refs.[13]and[3,17],respectively.

2.1 Classical Error-Locating Code

In the design of classical EL codes,the over-all code-word block of length n is divided into s sub-blocks that are mutually exclusive from each other.Then each subblock has a length of t=n/s.If an EL code can detect and locate a single sub-block that contains as many as e errors,then it is called an e-EL code.An e-EL code must satisfy the following conditions(see Ref.[13]):

(i)The syndrome resulting from the occurrence of e or fewer errors within any one sub-block must be distinct from the all-zeros syndrome.

(ii)The syndrome resulting from the occurrence of e or fewer errors within a single sub-block must be distinct from the syndrome resulting from any combination of e or fewer errors within any other sub-block.

Based on cyclic codes with generator polynomials g(x)over F2,a special class of binary EL codes can be derived as follows.

Theorem 1[13]If g(x)=g1(x)g2(x)···gv(x)is the product of distinct polynomials that are all irreducible over F2,and these polynomials all have the same period h.Let C=[h,h−p]be the cyclic code generated by g(x)whose minimum distance is d,and the check symbols arep=deg(g).Then there is an e-EL code with errorlocating abilities e=d−1 and length n=(h+1)m−1,the checking symbols are r=mp,m≥2 is an integer.

2.2 Quantum Error-Correcting Codes

Let C be the complex number field.For a positive integer n,let Vn=(C2)⊗n=C2nbe the n-th tensor product of C2.Let|αbe the vectors of the orthonormal basis of C2.For u,v∈F2,the unitary operator X(u)is de fi ned by X(u)|α=|α +u,and the unitary operator Z(v)is defi ned by Z(v)|α=(−1)v·α|α.Let a={a1,...,an}and b={b1,...,bn}be two vectors over GF(2).Denote byand Z(b)=Z(b1)the tensor products of n error operators.Then the setEn={X(a)Z(b)|a,b∈GF(2)n}is an error basis on Vn.The fi nite group Gn={±X(a)Z(b)|a,b∈GF(2)n}is the error group associated with the error basisEn.Then the Definition of QECCs can be given as follows.For simplicity,we only consider binary QECCs,i.e.,qubit systems.For the Definition of nonbinary QECCs,see Refs.[5,12].

Definition 1A binary quantum code of length n,denoted by[[n,k,d]],is a subspace Q of Vnover fi nite field F2with dimension 2kthat satis fi es

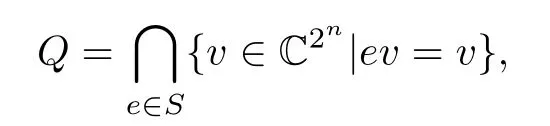
for some commutative subgroup S of Gn,which can detect at most d−1 qubits errors for d≥1,and can correct at mostqubits errors.

For a binary linear code C over F2,the dual of codes C is given by=0 for all x∈C}.If there exist two binary linear code C1and C2satisfyingthen there exists a QECC according to the following construction.

Theorem 2[Refs.[18–19],CSS Construction]Let C1and C2denote two binary linear codes with parameters[n,k1,d1]and[n,k2,d2],respectively,such thatThen there exists an[[n,k1+k2−n,d]]QECC with minimum distance d=min{wt(c)|c∈(C1)∪(C2)}.

Let C1be an e1-EL code and let C2be an e2-EL code C2,and the syndromes of C1and C2satisfy the conditions for error-locating codes,respectively.Ifthen there exists a quantum analog of error-locating codes which can locate up to e1numbers of bit errors and e2numbers of phase errors in a single sub-block by using the CSS construction.Therefore,we have the following result for the construction of QEL codes.

Corollary 1Let L1and L2be two e1-EL and e2-EL error-locating codes,respectively.Ifthen there is a quantum eq-EL code with eq=min{e1,e2},which can detect and locate a single sub-block containing up to eqquantum errors.

3 Quantum Error-Locating Codes

According to Corollary 1,QEL codes are constructed from classical EL codes that satisfy certain dual containing restriction.We show that,for an e-EL code derived from a binary cyclic code with generator polynomial g(x),the resultant e-EL code is dual contained if g(x)does not contain the(1+x)-factor.In order to get the dual-containing EL codes,we need a property of cyclic codes firstly.

Lemma 1 Let C be a binary cyclic code of length n such that gcd(2,n)=1,whose generator polynomial is g(x).Then C contains the all one codeword e=(1,1,...,1)if and only if the decomposition of g(x)does not contain the(1+x)-factor.

ProofWe represent the codeword e=(1,1,...,1)by a polynomial over the polynomial ring F2[x]/(xn−1)as follows:e(x)=1+x+ ···+xn−1=(xn− 1)/(1+x).The check polynomial of C is given by h(x)=(xn−1)/g(x).Then e(x)∈C⇔e(x)h(x)=(xn−1)·(xn−1)/(1+x)g(x)=0(mod xn−1).

Theorem 3 Let gcd(2,t)=1 and C be a binary cyclic code of length t whose generator polynomial is g(x)of degreep.Let g(x)=g1(x)g2(x)···gv(x)be a factorization of g(x)into distinct irreducible polynomials over F2.The minimum distance of C is d.If the decomposition of g(x)does not contain the(1+x)-factor,then there exists an e-QEL code Q=[[n,n−R]],where e=d−1,n=(t+1)m−1 and R=2mp,for any integer m ≥2,and Q has e quantum error-locating abilities.

Proof We denote the parity check matrix of C over F2by H.LetPjbe the j-th cyclic permutation matrix of order t,from right to left,for j=0,...,t−1.ThenPjsatis fi es=I for j=0,1,...,t−1,whereis a transpose and I is the identity matrix,and also satis fi es

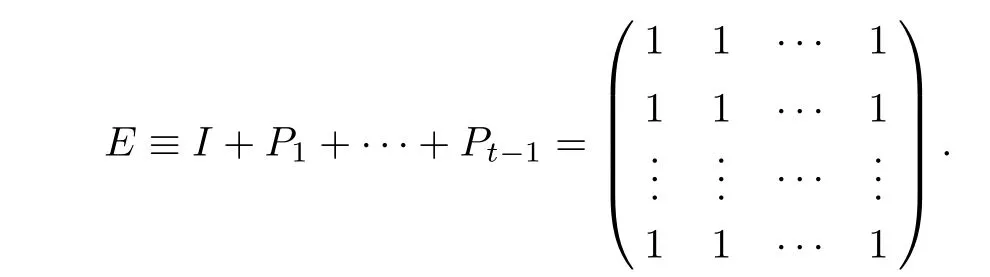
There exists an e-EL code L=[n,n−r]by Theorem 1,where e=d−1,n=(t+1)m−1,using r=mpcheck symbols,for any integer m≥2.Denote the parity check matrix of L by Hm.We illustrate the construction for the case m=2.Let

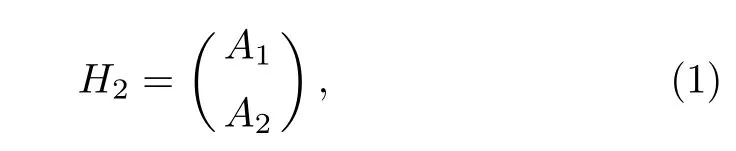
with

A1=(HOHHH··· H),

A2=(OHHHP1HP2··· HPt−1),where O is a zero matrix.

Firstly it is easy to verify that A1=O.Next,there is

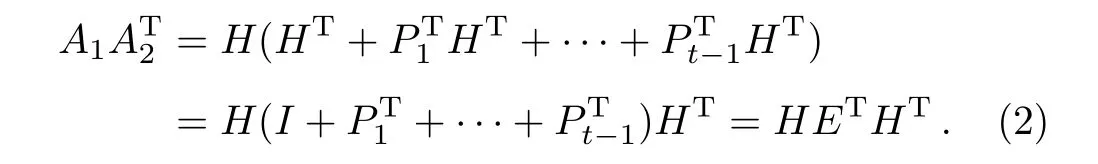
From Lemma 1,it is easy to see that HET=O,thus we have A1=O.Then we show that

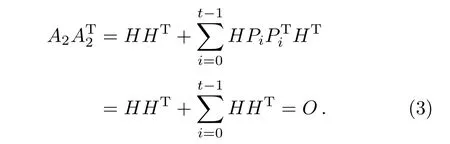
Therefore,we have H2=O.For the case of m＞2,the structure of the corresponding parity check matrix Hmis analogous to that of H2,but it allows all combinations of i submatrices to be zero(out of m),for i=0,1,...,m−1.Through analyzing the sub-block structure of Hm,it is not difficult to find that Hmis also equal to zero.Therefore we get L⊥⊆L for any integer m≥2.Then we can obtain an e-QEL code Q with parameters[[n,n−R]]by Corollary 1,where e=d−1,n=(t+1)m−1 and R=2mp,for any integer m ≥ 2,and Q has a quantum analog of e error-locating abilities.

We give two examples to illustrate the construction of QEL codes in Theorem 3,which can be seen as quantum analogs of the two families of classical EL codes in Ref.[13].

Example 1 We take the cyclic C=[s,1]code of minimum distance s such that s≥3 is a prime number,whose generator polynomial is g(x)=1+x+ ···+xs−1.The parity check matrix of C is given by

It is known that g(x)does not contain the(1+x)-factor.Hence we can obtain a quantum e-EL code with parameters

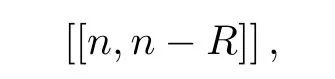
where

Let s=7,m=2,we can obtain a[[63,39]]code that can determine the location of any sub-block of width s=7 that has up to 6 quantum errors.In contrast,the quantum BCH[[63,39]]code can detect any 4 erroneous symbols in the whole block of 63.Now we can detect as many as 6 quantum errors in one sub-block,and we can also locate the erroneous sub-block at the same time.

Example 2Let g(x)be a single primitive irreducible polynomial over F2of degreep≥ 2.Let s=2p− 1,and de fi ne the class of classical EL codes with parameters as follows

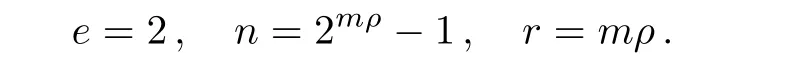
Since g(x)is a primitive irreducible polynomial andp≥ 2,we can obtain a quantum e-EL code with parameters

where

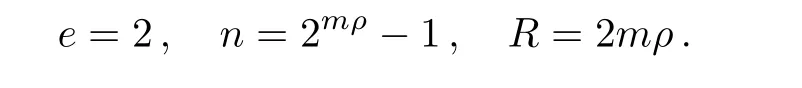
If let m=2 andp=3,then we can obtain a[[63,51]]QEL code.This code can locate any sub-block of length s=7 which has up to two errors.While letting m=3 andp=2,we can obtain another QEL code with the same parameters[[63,51]],which is able to locate any sub-block of length t=3 containing up to two errors.

4 Conclusion and Discussion

In this study,we have proposed the construction of QEL codes based on classical EL codes.The main technical contribution is that only if the generator polynomial g(x)of any classical EL codes does not contain the(1+x)-factor,then a QEL code with e error-locating abilities can be derived from the corresponding EL codes.This type of quantum codes can indicate the location of quantum errors in a single sub-block but without determining the precise erroneous symbol positions,and is useful to fault detecting in future quantum computers and quantum communications.

References

[1]A.M.Steane,Phys.Rev.Lett.77(1996)793.

[2]P.W.Shor,Phys.Rev.A 52(1995)R2493.

[3]D.Gottesman,Ph.D.Dissertation,California Institute of Technology,Pasadena(1997).

[4]A.R.Calderbank,E.M.Rains,P.W.Shor,etal.,IEEE Trans.Inf.Theory 44(1998)1369.

[5]A.Ketkar,A.Klappenecker,S.Kumar,etal.,IEEE Trans.Inf.Theory 52(2006)4892.

[6]D.Gottesman,Phys.Rev.A 54(1996)1862.

[7]M.Grassl and T.Beth,R.Soc.Lond.A 456(2000)2689.

[8]A.Thangaraj and S.W.McLaughlin,IEEE Trans.Inf.Theory 47(2001)1176.

[9]M.Grassl,T.Beth,and M.R¨oetteler,Int.J.Quantum Inf.2(2004)55.

[10]Z.Li and L.Xing,Acta Phys.Sin.57(2008)28.

[11]Z.Li and L.Xing,Acta Phys.Sin.56(2007)5602.

[12]J.Fan,H.Chen,and J.Xu,Quantum Inf.Comput.16(2016)423.

[13]J.K.Wolf and B.Elspas,IEEE Trans.Inf.Theory 9(1963)113.

[14]E.Fujiwara and M.Kitakami,IEEE Trans.Inf.Theory 40(1994)1857.

[15]V.V.Zyablov,Moscow,Ussr(1972).

[16]J.Maucher,V.V.Zyablov,and M.Bossert,IEEE Trans.Inf.Theory 46(2000)642.

[17]K.Feng and H.Chen,Quantum Error-Correcting Codes,Science Press,Beijing(2010)p.39.

[18]A.R.Calderbank and P.W.Shor,Phys.Rev.A 54(1996)1098.

[19]M.A.Nielsen and I.L.Chuang,Quantum Computation and Quantum Information,Cambridge University Press,Cambridge(2000)p.425.