New Exact Solutions of Time Fractional Gardner Equation by Using New Version of F-Expansion Method

Yusuf Pandir and Hasan Huseyin Duzgun

Department of Mathematics,Bozok University,66100,Yozgat,Turkey

1 Introduction

With knowledge of the physical and dynamic properties of the system that exists in nature can be made easily predictions about the current and future functioning.These properties are needed to identify fractional derivatives and integrals.Many events in the physical system can be explained using fractional order equations.Fractional order partial differential equations are used to obtain solutions to problems that have arisen in a number of different areas,such as dynamics,engineering,physics,chemistry,biology,signal processing,system identi fication,continuum mechanics,electromagnetics,control theory.There are different kinds of fractional derivatives such as Caputo derivative,[1]Riemann–Liouville derivative,[2]Kolwankar–Gangal(K-G)derivative,[3−4]Chens fractal derivative,[5−6]Cressons derivative,[7]and Jumaries modi fi ed Riemann–Liouville derivative.[8]Many methods have been suggested to acquire the exact solutions of the fractional order partial differential equations such as subequation method,[9−10]first integral method,[11−12]expfunction method,[13−14](G′/G)expansion method,[15−17]the extended trial equation method,[18]the modi fi ed trial equation method.[19−20]Also some approximation and numerical techniques have been used to solve fractional differential equations such as local fractional variational iteration method,[21]the fractional functional variable method,[22]local fractional Adomian decomposition method,[23−24]local fractional Fourier series method,[25]fi nite di ff erence method,[26]fi nite element method[27]and so on.The rest of the paper is organized as follows:In Sec.2 some basic Definitions of fractional derivatives have been given.Also developed new versions of F-expansion method for fractional differential equations have been presented.Then in Sec.3 we apply proposed method to time fractional derivative nonlinear Gardner equation.The paper ends in Sec.4 with conclusion.

2 Developed New Version ofF-Expansion Method

In this section, firstly some basic Definitions and important properties of the fractional derivates such as Jumarie modi fi ed fractional derivative,modi fi ed Riemann–Liouville derivative,Ji-Huan Hes fractional derivative are indicated.And then developed new version of F-expansion method is introduced.

Definition 1Let f be a continuous function and α∈(0,1).The Riemann–Lioville fractional derivative of order α is de fi ned by expression of Ref.[28]as follows:

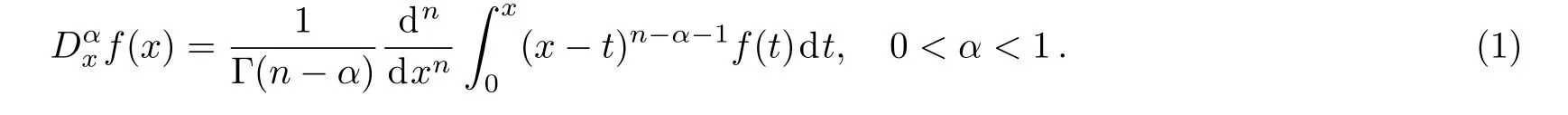
Definition 2Let f:[0,1]→ ℜ be a continuous function and α ∈(0,1).The Jumarie modi fi ed fractional derivative of order α may be de fi ned[29−30]as follows:

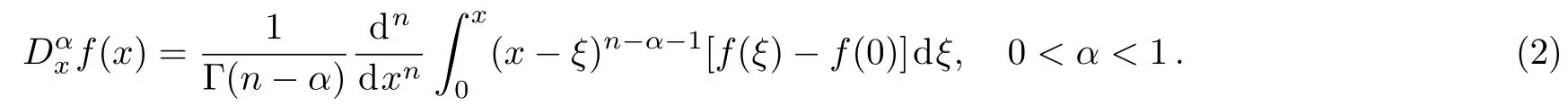
Definition 3Let f be a continuous function and α∈(0,1).Ji-Huan Hes fractional derivative de fi ned as[31]where f0(x,t)is a known function.

Some properties for the proposed modi fi ed Riemann–Liouville derivative are listed in Ref.[32]as follows:

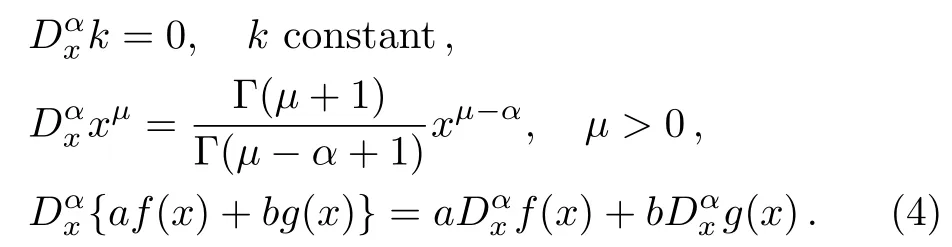
In this study,we used the following chain rule for fractional calculus

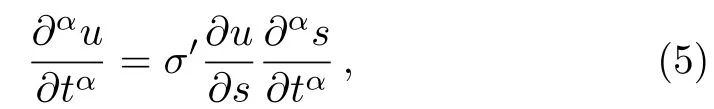
where σ′denotes the sigma index.[33−39]Using fractional complex transform and above modi fi ed chain rule we can easily convert fractional differential equations into ordinary differential equations.

For the given general nonlinear fractional differential equation of the type

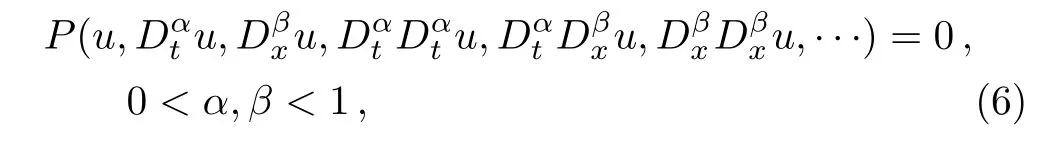
where u is an unknown function,andPis a polynomial of u and its partial fractional derivatives,in which the highest order derivatives and the nonlinear terms are involved.We seek the following travelling wave solutions:

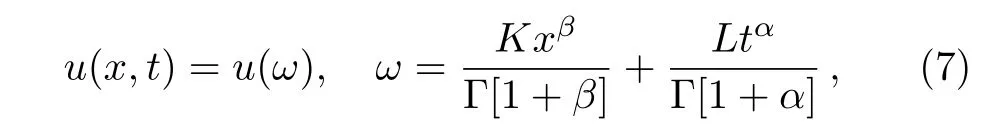
which are of important physical signi ficance,K and L are constants to be determined later.Then we can reduce Eq.(6)to nonlinear ordinary differential equation

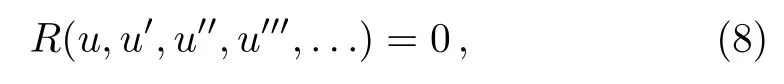
where the prime denotes the derivation with respect to ω.Introducing a new independent variables in the form

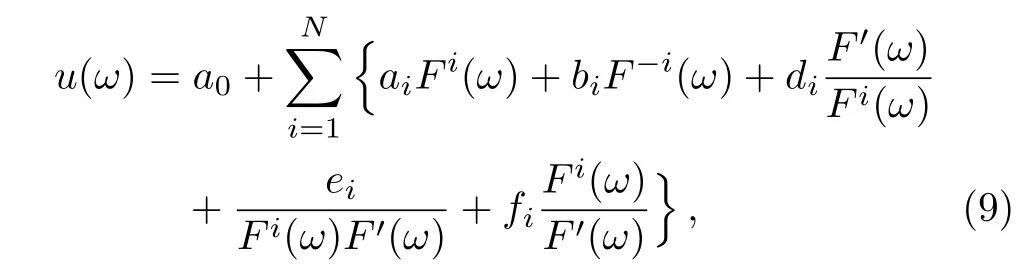
in which ai,bi,di,ei,fi(i=0,1,2,...,N)all constants to be determined later,F(ω)and F′(ω)in(9)satisfy

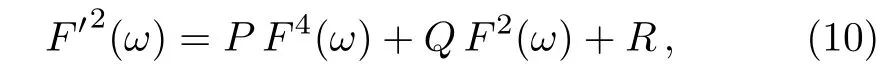
and hence holds for F(ω)and F′(ω)

whereP,Q and R are all parameters,the prime denotes d/dω.Given different values ofP,Q and R,the different Jacobi elliptic function solutions F′(ω)can be obtained from Eq.(10).

The balancing numbersNare positive integers,which can be determined by balancing the highest order derivative terms with highest power nonlinear terms in Eqs.(8).We substitute Eq.(9)and Eq.(11)into Eq.(8)computerized symbolic computation,equating to zero the coefficients of all power F′i(ω)Fj(ω)(i=0,1;j=0,±1,±2,...)yields a set of algebraic equations for ai,bi,di,ei,fi,and ω.

3 Time Fractional Nonlinear Gardner Equation

WeconsidertimefractionalnonlinearGardner equation[40]

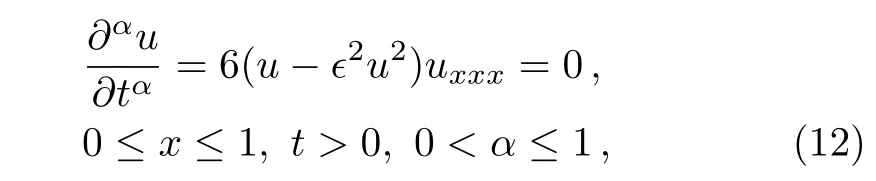
where x is the spatial variable and t represents time.We introduce the following fractional complex transformation

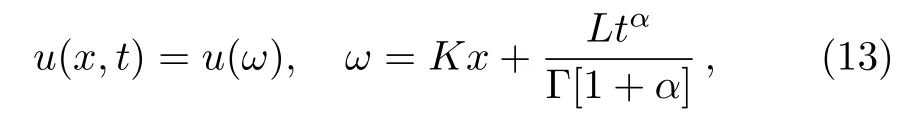
where K and L are constants.By using Eq.(13),Eq.(12)reduces a nonlinear ordinary differential equation

We integrate Eq.(14)with respect to ω once time we get following equation

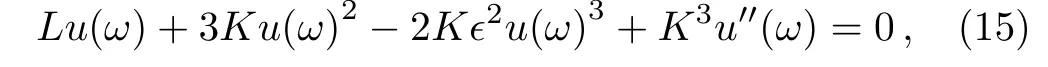
where the primes denote differentiations,K and L are arbitrary constants to be determined later.Balancing u′′and u3in Eq.(15),we getN=1,so the solution of Eq.(15)is of the form:

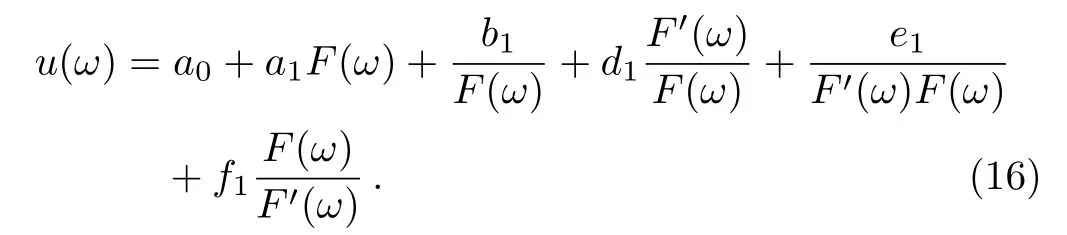
Considering Eqs.(10)–(11)and substituting Eq.(16)into Eq.(15)and setting each coefficients of F′i(ω)Fj(ω)(i=0,1;j=0,±1,±2,...)to zero,yields a set of equations for a0,a1,b1,d1,e1,f1,L,K the system of algebraic equations with the aid of Mathematica.If we select F(ω)=sn(ω),from(9)we getP=m2,Q= −(1+m2),R=1,so we get following cases namely:

Case 1

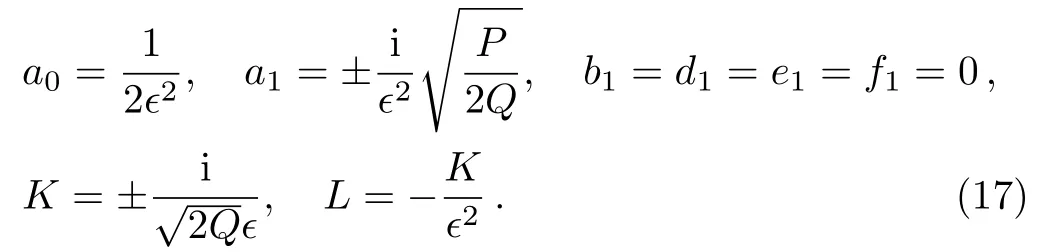
When we substitute Eq.(17)into Eq.(16),we obtain new types of exact solutions of Eq.(12)as follows:

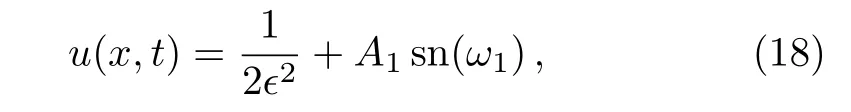
where

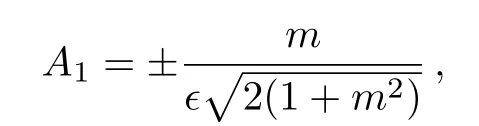
The graph of solution(18)is shown as Fig.1.

Fig.1 Graph of the solution(18)corresponding to the values α =0.01,0.50 and α =1 when m=0.2,ϵ=0.1.

Case 2

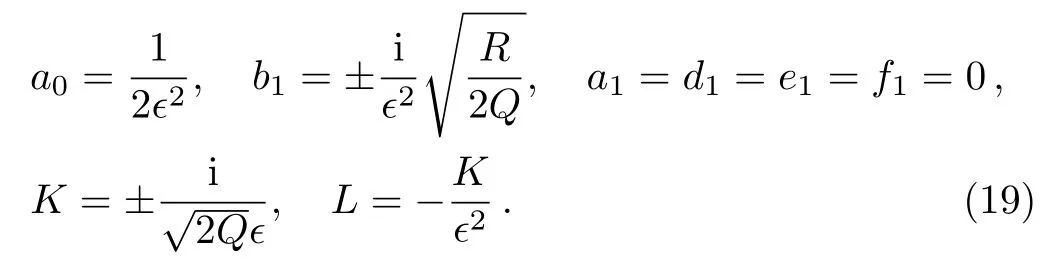
If we put Eq.(19)into Eq.(16),we get the Jacobi elliptic function solutions of Eq.(10)

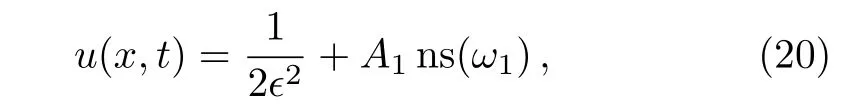
Case 3

When we replace Eq.(21)into Eq.(16),we gain following combined Jacobi elliptic function solution

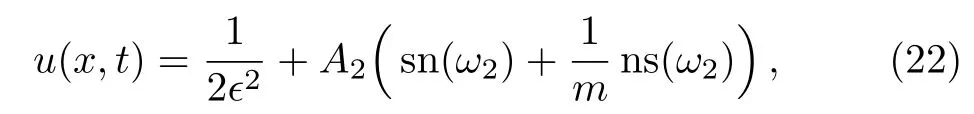
where

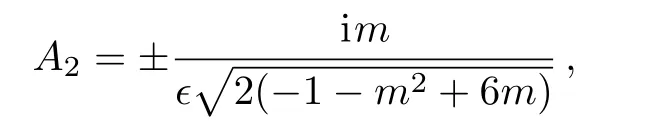
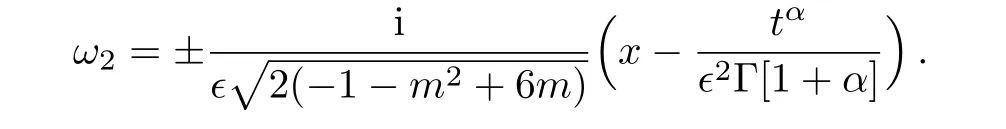
Case 4

When we replace Eq.(23)into Eq.(16),we find new exact solution name as combined Jacobi elliptic function solutions of Eq.(12)

where

The graph of solution(24)is shown as Fig.2.

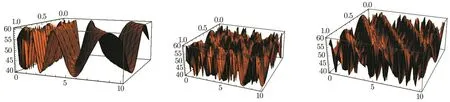
Fig.2 Graph of the solution(24)corresponding to the values α =0.01,0.50 and α =1 when m=0.2,ϵ=0.1.

Case 5

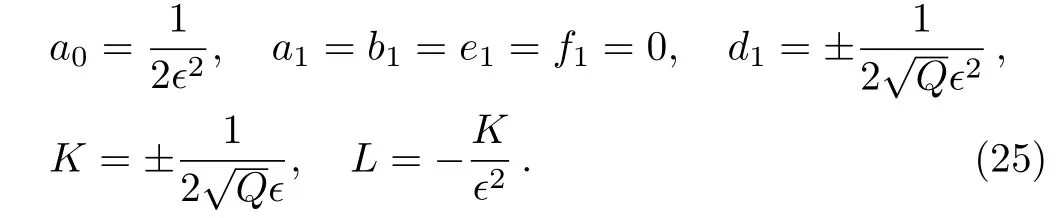
When we slot Eq.(25)into Eq.(16),we obtain following new combined Jacobi elliptic function solution of Eq.(12)

where

Case 6

When we replace Eq.(27)into Eq.(16),we get different type of Jacobi elliptic function solution of Eq.(12)

where A5=

Case 7

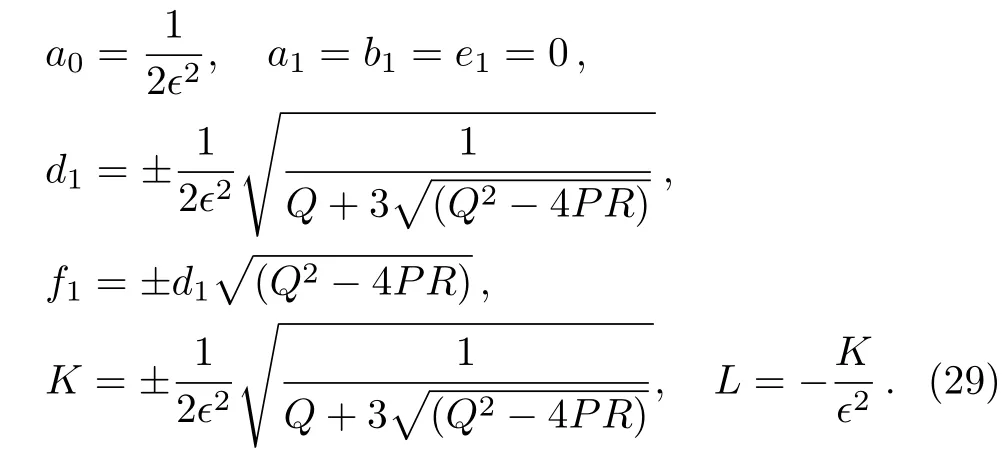
When we put Eq.(29)into Eq.(16),we find the combined Jacobi elliptic function solution of Eq.(12)

where

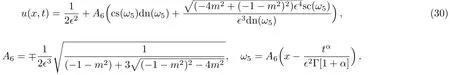
Case 8

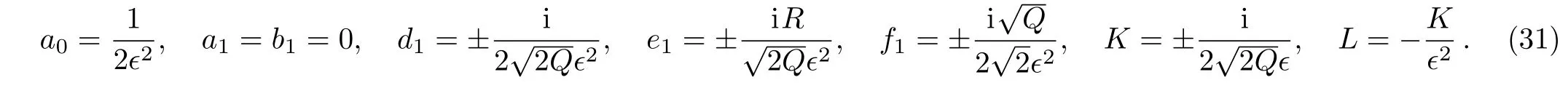
When we substitute Eq.(31)into Eq.(16),we obtain following multiple combined Jacobi elliptic function solution of Eq.(12)

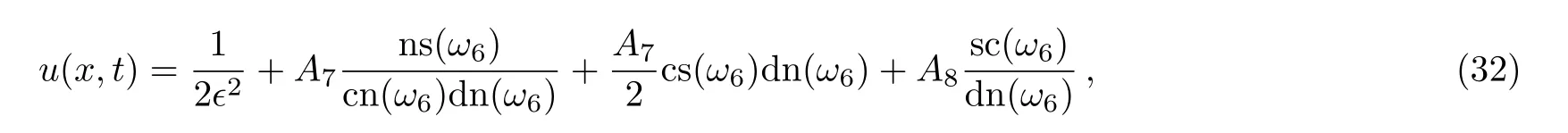
where

The graph of solution(32)is shown as Fig.3.

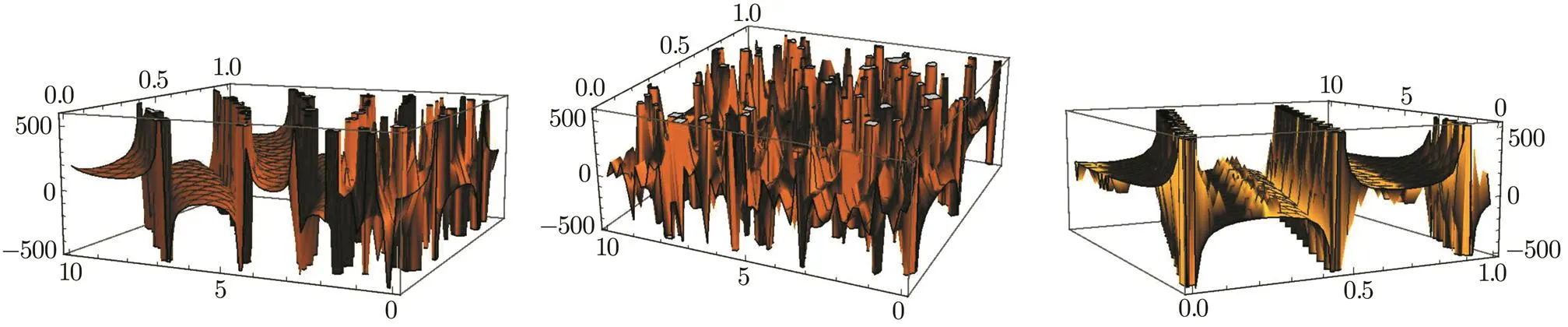
Fig.3 Graph of the solution(32)corresponding to the values α =0.01,0.50 and α =1 when m=0.2,ϵ=0.1.

Case 9

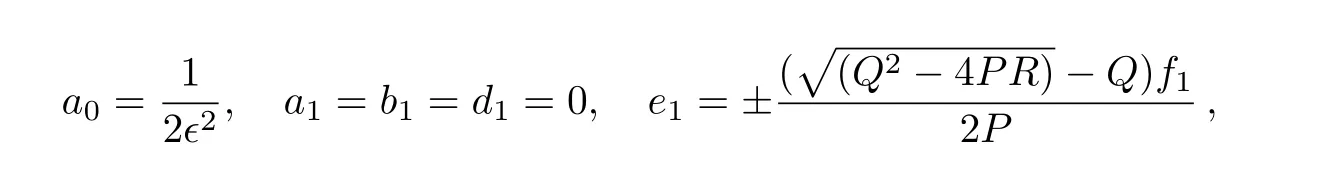
When we put into place Eq.(33)into Eq.(15),we find new multiple combined Jacobi elliptic function solution of Eq.(12)

where

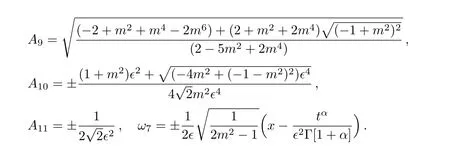
Case 10

When we replace Eq.(35)into Eq.(16),we obtain new type combined Jacobi elliptic function solutions of Eq.(12)

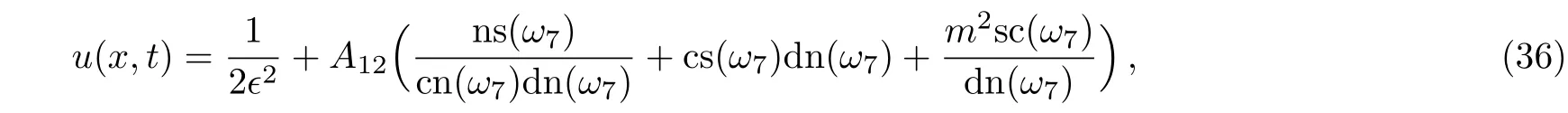
whereThe graph of solution(36)is shown as Fig.4.

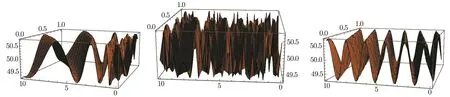
Fig.4 Graph of the solution(36)corresponding to the values α =0.01,0.50 and α =1 when m=0.2,ϵ=0.1.

Remark We have obtained different solutions with the solutions in Refs.[41–42].Moreover we have also presented in Cases 6–10 that do not exist in literature,because our method is more general form of F-expansion method.

4 Conclusion

In this paper,the new version of F-expansion method has been successfully implemented to achieve new exact solutions of the time fractional Gardner equation.This method makes it possible to obtain new function solutions.The obtained results for partial differential equations of fractional order seem to be very different and interesting.These solutions include single,combined and multiple combined Jacobi elliptic function solutions.Therefore,the present study was undertaken an enterprise to fi ll the gap in the related literature.If we place the parameters in the obtained Jacobi elliptic functions solutions as special values,a variety of special solutions like different solitary wave solutions are obtained.

References

[1]I.Podlubny,Fractional differential Equations,Academic Press,San Diego(1999).

[2]R.Metzler and J.Klafter,Phys.Rep.339(2000)1.

[3]K.M.Kolwankar and A.D.Gangal,Phys.Rev.Lett.80(1998)214.

[4]G.C.Wu,Comput.Math.Appl.61(2011)2186.

[5]H.G.Sun and W.Chen,Sci.China Ser.E 52(2009)680.

[6]W.Chen and H.G.Sun,Modern Phys.Lett.B 23(2009)449.

[7]J.Cresson,J.Math.Phys.44(2003)4907.

[8]G.Jumarie,Comput.Math.Appl.51(2006)1367.

[9]S.Zhang and H.Q.Zhang,Phys.Lett.A 375(2011)1069.

[10]B.Zheng and C.Wen,Adv.Di ff.Eq.2013(2013)199.

[11]B.Lu,J.Math.Anal.Appl.395(2012)684,693.

[12]M.Eslami,B.F.Vajargah,M.Mirzazadeh,and A.Biswas,Indian J.Phys.88(2)(2014)177.

[13]S.Zhang,Q.A.Zong,D.Liu,and Q.Gao,Commun.Frac.Calculus 1(2010)48.

[14]B.Zheng,Sci.World J.2013(2013)465723.

[15]B.Zheng,Commun.Theor.Phys.58(2012)623.

[16]E.M.E.Zayed,Y.A.Amer,and R.M.A.Shohib,Int.J.Eng.Appl.Sci.4(2014)18.

[17]A Bekir and O.Guner,Chin.Phys.B 22(2013)110202.

[18]Y.Pandir,Y.Gurefe,and E.Misirli,Discrete Dyn.Nat.Soc.2013(2013)491359.

[19]H.Bulut,H.M.Baskonus,and Y.Pandir,Abstract Appl.Anal.2013(2013)636802.

[20]Y.Pandir,Y.Gurefe,and E.Misirli,Int.J.Model.Opt.3(2013)349.

[21]X.J.Yang,Adv.Comput.Math.Appl.1(2012)86.

[22]W.Liu and K.Chen,Pramana.J.Phys.81(2013)377.

[23]X.J.Yang and Y.D.Zhang,Adv.Inf.Tech.Manag.1(2012)158.

[24]X.J.Yang,D.Baleanu,and W.P.Zhong,Proceed.Romanian Acad.Ser.A 14(2013)127.

[25]M.S.Hu,R.P.Agarwal,and X.J.Yang,Abstract.Appl.Anal.2012(2012)15.

[26]G.H.Gao,Z.Z.Sun,and Y.N.Zhang,J.Comput.Phys.231(7)(2012)2865.

[27]W.Deng,SIAM J.Numer.Anal.47(2008)204.

[28]J.H.He,Int.J.Theor.Phys.53(2014)3698.

[29]G.Jumarie,Comput.Math.Appl.51(2006)1367.

[30]G.Jumarie,Appl.Math.Lett.19(2006)873.

[31]F.J.Liu,Z.B.Li,S.Zhang,and H.Y.Liu,Thermal Sci.19(2015)1155.

[32]G.Jumarie,J.Appl.Math.Comput.24(2007)31.

[33]J.H.He,S.K.Elagan,and Z.B.Li,Phys.Lett.A 376(2012)257.

[34]Y.Hu and J.H.He,Thermal Sci.20(2016)773.

[35]F.J.Liu,P.Wang,Y.Zhang,H.Y.Liu,Thermal Sci.20(2016)779.

[36]K.L.Wang and S.Y.Liu,Thermal Sci.20(2016)793.

[37]K.L.Wang and S.Y.Liu,Nonlinear Sci.Lett.A 7(2016)135.

[38]K.Sayevand and K.Pichaghchi,Nonlinear Sci.Lett.A 7(2016)77.

[39]M.A.Abdou,M.T.Attia,and A.Elhanbaly,Nonlinear Sci.Lett.A 7(2016)86.

[40]O.S.Iyiola and O.G.Olayinka,Ain Shams Eng.J.5(2014)999.

[41]O.Sahoo and S.S.Ray,Math.Meth.Appl.Sci.40(2007)106.