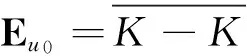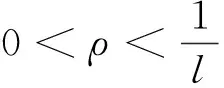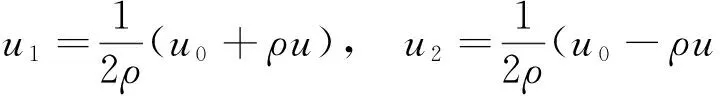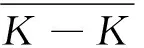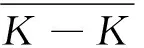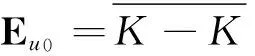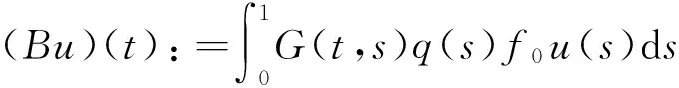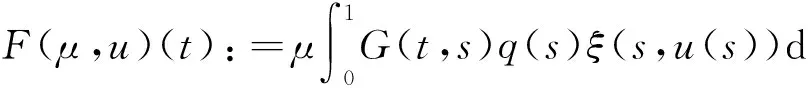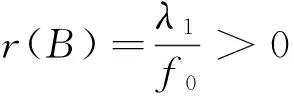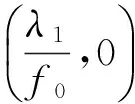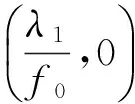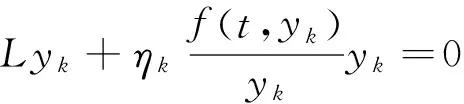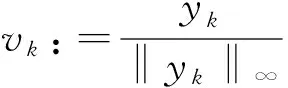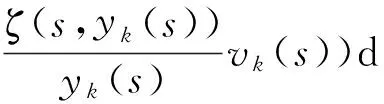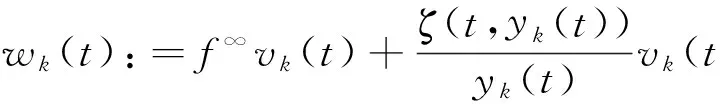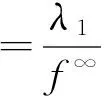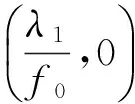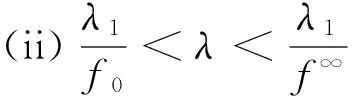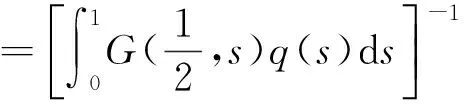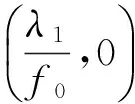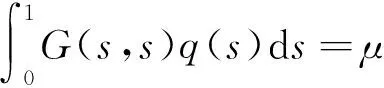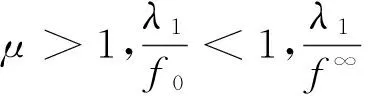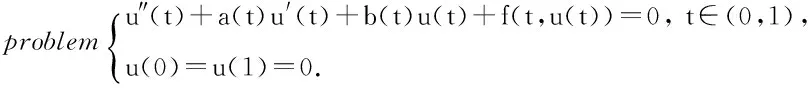一类奇异边值问题正解的存在性及多解性

2017-05-18闫东明

浙江大学学报（理学版） 2017年3期

关键词：边值问题范数特征值

闫东明

(浙江财经大学数据科学学院，浙江杭州 310018)

一类奇异边值问题正解的存在性及多解性

闫东明

(浙江财经大学数据科学学院，浙江杭州 310018)

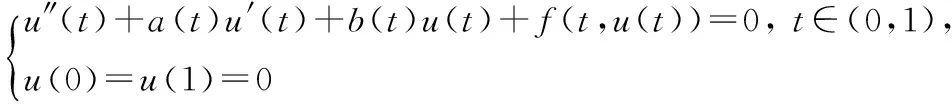
奇异边值问题;全局分歧;正解;多解性;第1特征值

JournalofZhejiangUniversity(ScienceEdition), 2017,44(3):281-286，328

0 引言

奇异边值问题因其具有的物理意义引起了人们的广泛关注,并且此类问题的相关研究也取得了许多深刻的结果[1-8].同时，鉴于正解及多个正解的实际意义,奇异边值问题正解及多个正解存在性的研究显得更为活跃.文献[6]研究了奇异边值问题

(1)

正解的存在性.在非线性项f满足非负性及一些局部增长性条件下,获得了奇异边值问题(1)的一个正解的存在性结果,并给出了问题(1)有正解存在和无正解存在时非负参数λ的取值范围.文献[8]研究了带一般微分算子的奇异边值问题：

(2)多个正解的存在性.通过构造奇异边值问题(2)的格林函数,并运用Leggett-Williams不动点定理,在非线性项f满足非负性条件及一些局部条件下,获得了奇异边值问题(2)多个正解的存在性结果.

另外,文献[9-10]运用Rabinowitz全局分歧理论以及区间分歧方法，对Dirichlet边值问题正解集的结构和全局分歧进行了讨论,获得了大量有价值的结果.

上述文献从不同的角度丰富了常微分方程奇异边值问题正解的存在性理论.然而,这些研究所得到的奇异边值问题有正解及多个正解存在的充分性条件中所涉及的数值均非最优,且所得充分性条件与奇异边值问题对应的线性问题的第1个特征值之间没有建立联系，而边值问题对应的线性问题的特征值在边值问题正解及多个正解存在性的研究中是一个很本质的量.本文运用Dancer全局分歧定理[11]对二阶常微分方程奇异边值问题(2)进行研究，试图给出此类问题有正解存在且与其相应线性问题第1个特征值有关的充分条件,以及说明这些充分条件中所涉及的值是最优的.无论是方法还是所得结果,本研究都将进一步丰富二阶常微分方程奇异边值问题正解的存在性理论.

本文总假定

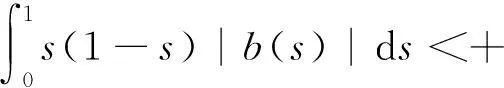
(A2)f:[0,1]×[0,+∞)→[0,+∞)连续.

1 预备知识及引理

记C[0,1]为定义在[0,1]上的连续实值函数构成的集合,定义范数

‖x‖∞=sup{|x(t)||t∈[0,1]},

则C[0,1]为Banach空间.记[0,1]上的所有绝对连续函数全体为AC[0,1].令

ACloc[0,1)={u|u|[0,d]∈AC[0,d],[0,d]⊆[0,1)},

ACloc(0,1]={u|u|[d,1]∈AC[d,1],[d,1]⊆(0,1]}，

方便起见，记

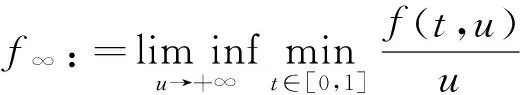
引理1[8]假设(A1)成立.则

(i)初值问题

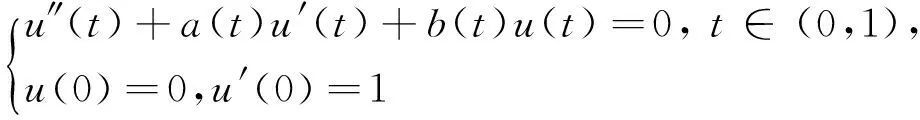
有唯一解α∈AC[0,1]∩C1[0,1)且α′∈ACloc[0,1);

(ii)初值问题

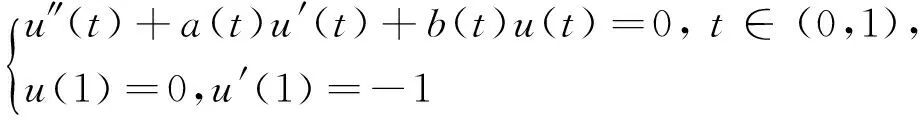
有唯一解β∈AC[0,1]∩C1(0,1]且β′∈ACloc(0,1];

(iii)α在[0,1]非减,β在[0,1]非增.

设

引理2 设(A1)成立.则G具有以下性质:

(i)G(t,s)>0, (t,s)∈(0,1)×(0,1);

(ii)G(t,s)≤G(t,t), (t,s)∈[0,1]×[0,1];

(iii)G(t,s)≥δt(1-t)G(s,s), (t,s)∈[0,1]×[0,1],其中δ>0为常数.

证明由引理1易证(i)、(ii).以下证(iii)成立.

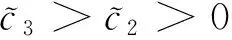
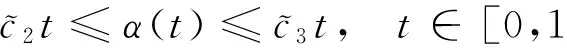
(3)

(4)

由G的定义、引理1以及式(3)和(4)，有

即

G(t,s)≥δt(1-t)G(s,s), (t,s)∈[0,1]×[0,1],

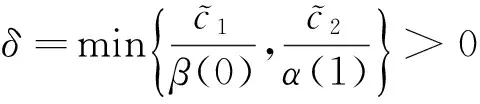
定义P={u∈C[0,1]:u(t)≥0,t∈[0,1],u(0)=u(1)=0}.则P是C[0,1]中的一个锥.设

(5)

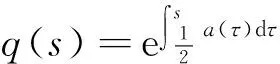
根据Krein-Rutmann定理[11-12],有下述引理.

令Eu0={u|u∈C[0,1]且存在λ>0使得

-λt(1-t)≤u(t)≤λt(1-t),t∈[0,1]}.

若u∈Eu0,则令u的范数为

‖u‖u0= inf{λ|λ>0,-λt(1-t)≤

u(t)≤λt(1-t),t∈[0,1]}.

(6)

此处‖u‖u0为u的u0-范数,相关内容可参见文献[14].

引理4 (Eu0,‖·‖u0)是Banach空间.

证明设{un}是(Eu0,‖·‖u0)中的Cauchy列.则有

‖un-um‖→0,n,m→∞.

(7)

由式(6)和(7),对∀ε>0，存在N>0使得

-εt(1-t)≤un(t)-um(t)≤εt(1-t),

t∈[0,1], ∀n,m>N.

(8)

从而,

即{un}是(C[0,1],‖·‖∞)中的Cauchy列.根据(C[0,1],‖·‖∞)的完备性,存在u0∈C[0,1]使得

‖un-u0‖∞→0,n→∞.

在式(8)中令m→∞，则有

-εt(1-t)≤un(t)-u0(t)≤εt(1-t),

t∈[0,1],(n>N),

即

‖un-u0‖u0≤ε,n>N.

因此,对Cauchy列{un}⊂(Eu0,‖·‖u0),存在u0∈Eu0使得

‖un-u0‖u0→0,n→∞.

所以,(Eu0,‖·‖u0)是Banach空间.引理证毕.

引理5 设(A1)成立,算子T如式(5)所定义.则T的谱半径r(T)>0,且T有一个正的特征函数φ1对应于其第1个特征值λ1=(r(T))-1,即φ1=λ1Tφ1.

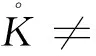
下证T是一个强正算子.设u∈K{θ}.则u在[0,1]上不恒为0,并且由K的定义知,存在λ0>0,使得

0≤u(t)≤λ0t(1-t),t∈[0,1].

(9)

由引理1以及式(3)、(4)和(9)，有

c2u[t(1-t)],t∈[0,1]

和

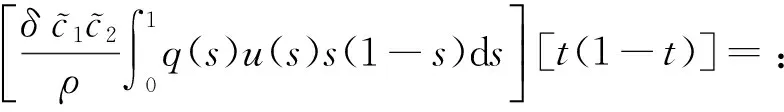
c1u[t(1-t)],t∈[0,1],

其中,

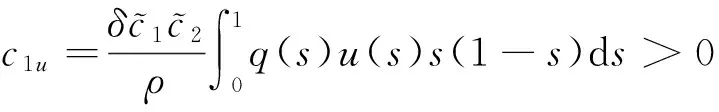
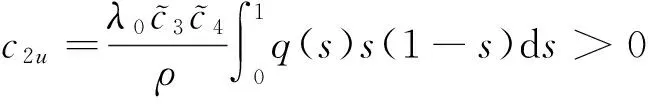
ρ,δ见引理2.从而,对u∈K{θ}存在常数c1u,c2u>0,使得

c1u[t(1-t)]≤(Tu)(t)≤c2u[t(1-t)],t∈[0,1],

即

所以T是一个强正算子.

由引理3可知,T的谱半径r(T)≠0,且T有一个正的特征函数φ1对应于其第1个特征值λ1=(r(T))-1,并且满足φ1=λ1Tφ1.引理证毕.

注1 由引理5可知,当条件(A1)成立时,线性特征值问题

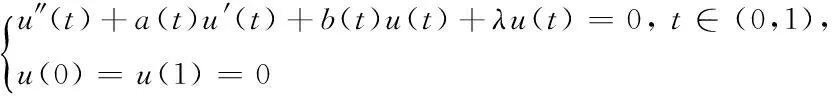
的第1个特征值λ1是大于0的,并且λ1所对应的特征函数φ1为正.

下面叙述一个关于参数化非线性算子方程正解集合的全局结构.此结果为Dancer全局分歧定理[11]的推论.

假设E为一个实Banach空间,其上范数为‖·‖.令K⊂E为一个锥,若A([0,∞)×K)⊂K，则称非线性映射A:[0,∞)×K→E是正的.若算子A连续,并且把[0,∞)×K中的有界子集映为E中的相对紧集，则称上述非线性映射A为K-全连续的.最后,对于定义在E上的连续线性算子B,用r(B)表示算子B的谱半径.

引理6[11]假设

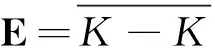
(ii)A:[0,∞)×K→E为K-全连续的正算子.对任意的λ∈R,有A(λ,0)=0;对任意的u∈K,有A(0,u)=0,且

A(λ,u)=λBu+F(λ,u),

其中B:E→E为定义在E上的强正线性紧算子且满足r(B)>0,F:[0,∞)×K→E满足:当‖u‖→0时,‖F(λ,u)‖=o(‖u‖)对λ局部一致成立.

则存在

u≠0}∪{(r(B)-1,0)}

的一个无界连通子集C,使得(r(B)-1,0)∈C.

2 主要结果及其证明

定理1 设(A1)和(A2)成立,λ1=(r(T))-1.若

f∞<λ1

(10)

或

f0<λ1

(11)

成立,则奇异边值问题(2)至少有1个正解.

注2 定理1中充分性条件(10)、(11)与奇异边值问题(2)对应的线性问题的第1个特征值建立起了联系.

注3 条件(10)、(11)中涉及的值λ1是最优的.若f∞=λ1=f0或f0=λ1=f∞,则奇异边值问题(2)正解的存在性不能保证.考虑如下边值问题:

u″(t)+a(t)u′(t)+b(t)u(t)+λ1u(t)+

ρ(u(t))=0,t∈(0,1),

(12)

u(0)=u(1)=0,

(13)

其中,

证明仅给出式(10)成立时的证明，式(11)可类似证得.

为了研究问题(2)正解的存在性,考虑以下参数化问题：

(14)

令

f(t,s)=f0s+ξ(t,s),f(t,s)=f∞s+ζ(t,s).

(15)

则

(16)

于是,参数化问题(14)可重写为

(17)

对空间Eu0以及其上的锥K，有

此闭包在u0-范数‖·‖u0下取得.事实上,设u∈Eu0，则存在常数l>0，使得

-l[t(1-t)]≤u(t)≤l[t(1-t)],t∈[0,1].

-(1+ρl)[t(1-t)]≤[t(1-t)±ρu(t)]≤

(1+ρl)[t(1-t)],t∈[0,1],

(18)

[t(1-t)±ρu(t)]≥(1-ρl)[t(1-t)]≥0,

t∈[0,1],

(19)

令u0(t)=t(1-t),t∈[0,1].则由式(18)和(19),有

u0±ρu∈K.

令

则u1,u2∈K,且满足

u=u1-u2,

即u∈K-K,从而有

另一方面,由空间(Eu0,‖·‖u0)的完备性(见引理4),可推得

u=A(μ,u),

(20)

其中，

A(μ,u)=μBu+F(μ,u),

而

‖F(μ,u)‖u0=o(‖u‖u0)

令

Φ+:={u∈C[0,1]:u(t)>0,t∈[0,1],

u(0)=u(1)=0}.

(21)

f∞<λ1

即

可推得当μ=1时,问题(14)即原问题(2)至少有1个正解u存在.

假设(ηk,yk)∈C+,并且满足|ηk|+‖yk‖∞→∞,k→∞.下面分2步来证明.

第1步证明{ηk}有界.

反设ηk→∞,k→∞.则易证yk在区间[0,1]上变号.事实上,由(ηk,yk)∈C+有

(22)另一方面,由假设(A2)可知，存在e∈C[0,1],e(t)>0,t∈[0,1],使得

由上述事实以及ηk→∞,k→∞的假设可得

于是,由Sturm比较定理可知，对充分大的k,yk在区间[0,1]中至少有1个零点,这与yk>0矛盾!因此,{ηk}是有界的.进一步,由连通分支C+的无界性，可知‖yk‖∞→∞,k→∞.

由式(15)以及(ηk,yk)∈C+，知(ηk,yk)(k∈N)也满足

(23)

令

则式(23)可变为

(24)

易知式(24)等价于

(25)

令

因为f(t,yk(t))=f∞yk(t)+ζ(t,yk(t)),所以由式(16)以及事实yk(t)>0,t∈[0,1]可推知:

这意味着存在一个不依赖于k的函数σ∈C[0,1],使得

于是{wk(t)}(k∈N)在C[0,1]中一致有界.并且,不难验证

由C1[0,1]紧嵌入C[0,1]，说明存在vk的子列(不妨仍记为vk),使得对某个v*∈C[0,1]及η*∈[0,∞),有vk→v*且ηk→η*(k→∞).对式(25)运用Lebesgue控制收敛定理可得

上式蕴含了v*∈C2[0,1],且满足

于是,

由定理1易得如下推论.

推论1 设(A1)和(A2)成立,λ1=(r(T))-1.若以下两条件之一成立:

则奇异特征值问题

至少有1个正解.

定理2 设(A1)和(A2)成立,λ1=(r(T))-1.若以下两条件之一成立:

(i)f0>λ1,f∞>λ1,且存在η*>0,使得f(t,u)

(ii)f0<λ1,f∞<λ1,且存在λ*>0,使得f(t,u)>B*λ*,(t,u)∈[0,1]×[0,λ*],

其中，

则奇异问题(2)至少有2个正解u1,u2.

证明仅给出(i)成立时的证明.(ii)可类似证得.

由定理1的证明知,参数化问题

设(μ,u)∈C+,且满足‖u‖∞=η*.则有

(26)

因此,由式(26)和条件(i)可得

f(t,u(t))

(27)

由引理2的(ii)以及式(27),对满足‖u‖∞=η*的(μ,u)有

从而,对满足‖u‖∞=η*的(μ,u)一定有

μ>1.

又由假设条件(i)可得

(1,u1),(1,u2)∈C+,

且满足‖u1‖∞<η*,‖u2‖∞>η*,即问题(2)有2个正解.定理证毕.

[1]O’REGAND.SingularDirichletboundaryvalueproblemsI.Superlinearandnonresonantcase[J]. Nonlinear Analysis,1997,29:221-245.

[2] ASAKAWA H. Nonresonant singular two-point boundary value problems [J]. Nonlinear Analysis,2001,44:791-809.

[3] XU X, MA J P. A note on singular nonlinear boundary value problems [J]. J Math Anal Appl,2004,293:108-124.

[4] HAN G D, WU Y. Nontrivial solutions of singular two-point boundary value problems with sign-changing nonlinear terms [J]. J Math Anal Appl,2007,325:1327-1338.

[5] DALMASSO R. Positive solutions of singular boundary value problems [J]. Nonlinear Analysis,1996,27:645-652.

[6] AGARWAL R P, WONG F H, LIAN W C. Positive solutions for nonlinear singular boundary value problems [J]. Appl Math Letters,2002,130(2/3):225-234.

[7] HA K S, LEE Y H. Existence of multiple positive solutions of singular boundary value problems [J]. Nonlinear Analysis,1997,28(8):1429-1438.

[8] LI J M, WANG J X. Triple positive solutions for a type of second-order singular boundary problems [J]. Boundary Value Problems,2010,2010(1):1-14.

[9] MA R Y, THOMPSON B. Multiplicity results for second-order two-point boundary value problems with superlinear or sublinear nonlinearities [J]. J Math Anal Appl,2005,303:726-735.

[10] MA R Y. Global behavior of the components of nodal solutions of asymptotically linear eigenvalue problems [J]. Applied Mathematics Letters,2008,21:754-760.

[11] DANCER E. Global solution branches for positive mappings [J]. Arch Rat Mech Anal,1973,52:181-192.

[12] ZEIDLER E. Nonlinear Functional Analysis and Its Applications, I. Fixed-Point Theorems[M]. New York: Springer-Verlag,1985.

[13] DEIMLING K. Nonlinear Functional Analysis[M]. New York: Springer-Verlag,1985.

[14] GUO D, LAKSHMIKANTHAM V. Nonlinear Problems in Abstract Cones[M]. New York: Academic Press,1988.

YANDongming

(School of Mathematics and Statistics, Zhejiang University of Finance and Economics, Hangzhou 310018, China)

Existenceofsingleandmultiplepositivesolutionsofsingularboundaryvalueproblem.