2类特殊图中的完美匹配数

2017-05-18唐保祥任韩

浙江大学学报（理学版） 2017年3期

关键词：数目情形顶点

唐保祥，任韩

(1.天水师范学院数学与统计学院，甘肃天水 741001; 2.华东师范大学数学系，上海 200062)

2类特殊图中的完美匹配数

唐保祥1，任韩2

(1.天水师范学院数学与统计学院，甘肃天水 741001; 2.华东师范大学数学系，上海 200062)

图的完美对集计数问题已经被证实是NP-难的,因此要得到一般图的完美匹配数目非常困难.用划分、求和、再递推的方法给出了4-1-nC10和2-nT2图完美匹配数目的计算公式.该方法可计算许多图类的所有完美匹配的数目,使得到一般的有完美匹配图的所有完美匹配数目成为可能.

划分; 递推式; 完美匹配

Journal of Zhejiang University(Science Edition), 2017,44(3):266-269

0 引言

图的完美匹配计数已经被证实是NP-难问题,因此要得到一般图的完美匹配数目是非常困难的.该问题在蛋白质结构预测、量子化学、晶体物理学和计算机科学等领域都有重要应用,对此问题的研究具有非常重要的理论价值和现实意义[1-9].本文用划分、求和、再递推的方法分别给出了4-1-nC10和2-nT2图的完美匹配数目的计算公式.该方法能够计算许多类图的所有完美匹配的数目.

定义1 若G图的2个完美匹配M1和M2中有一条边不同,则称M1和M2是G的2个不同的完美匹配.

定义2 设2条长为n的路：P1=u1u2…un+1,P2=v1v2…vn+1, 分别连接路P1与P2的顶点ui与vi(i=1,2,…,n+1)得到的图,称长为n的梯子,记为Tn.

n个长为10的圈记为

Ci=ui1ui2ui3vi2wi3wi2wi1wi4vi1ui4(i=1,2,…,n).

连接圈Ci上顶点vi1与vi2,连接圈Ci与Ci+1的顶点ui2与ui+1,1,ui3与ui+1,4,wi3与wi+1,4,wi2与wi+1,1(i=1,2,…,n-1),再分别连接圈C1与Cn的顶点u14与w14,u11与w11,un3与wn3,un2与wn2,得到的图记为4-1-nC10,如图1所示.

图1 4-1-nC10图Fig.1 Graph of 4-1-nC10

图2 2-nT2图Fig.2 Graph of 2-nT2

1 结果及其证明

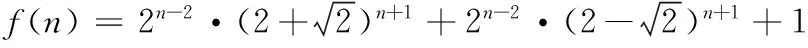
证明 4-1-nC10图是3正则3边连通图,显然存在完美匹配.欲求f(n),需定义G1,G2,G3图,并分别求出其完美匹配的数目.4-1-nC10图删除边u11w11,u14w14后得到的图记为G;将路u1u2vw的顶点u1,u2,w分别与G图的顶点u11,u14,w14连接，得到的图记为G1;将路uvw1w2的顶点u,w1,w2分别与G图的顶点u14,w14,w11连接，得到的图记为G2;将路u1u2的顶点u1,u2分别与G图的顶点u11,u14连接,再将路w1w2的顶点w1,w2分别与G图的顶点w14,w11连接，得到的图记为G3;G1,G2,G3图分别如图3～5所示.显然G1,G2,G3图都存在完美匹配,且G1≅G2.

图3 G1图Fig.3 Graph of G1

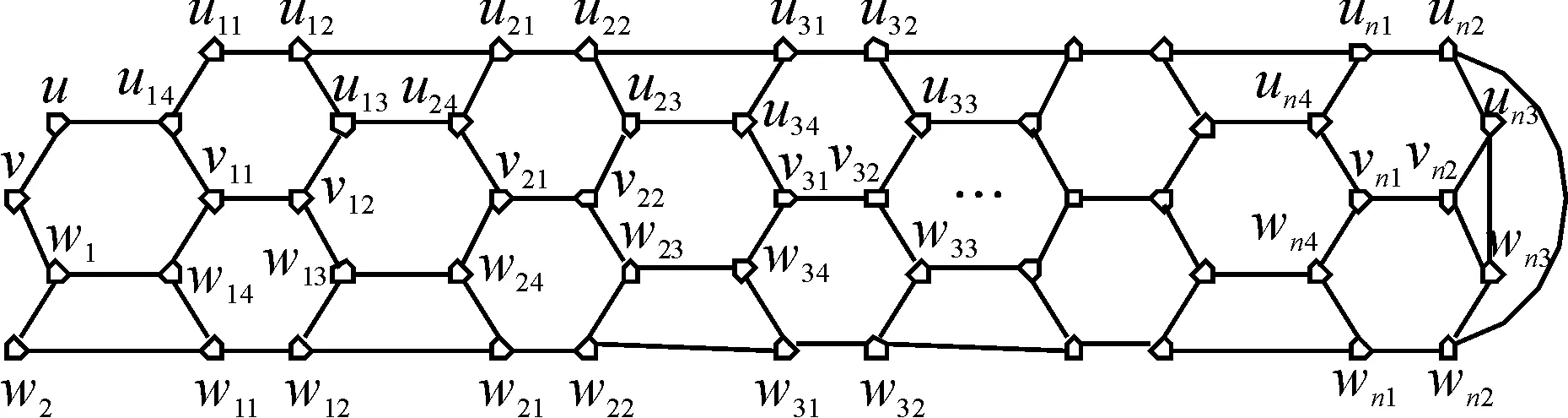
图4 G2图Fig.4 Graph of G2

图5 G3图Fig.5 Graph of G3

设G1,G2,G3图的完美匹配数分别为a(n),b(n),c(n),则a(n)=b(n).

G1图的完美匹配按饱和顶点u1可划分为以下6种情形:

情形1 由c(n)的定义,G1图包含边u1u11,u2u14,vw,v11v12,w14w11的完美匹配数为c(n-1).

情形2 由a(n)的定义,G1图包含边u1u11,u2u14,vw,v11w14,w11w12的完美匹配数为a(n-1).

情形3 由a(n)的定义,G1图包含边u1u11,u2v,ww14,v11w14,w11w12的完美匹配数为a(n-1).

情形4 由b(n)的定义,G1图包含边u1u11,u2u14,vw,v11w14,w11w12的完美匹配数为b(n-1),又a(n)=b(n),所以b(n-1)=a(n-1).

情形5 由c(n)的定义,G1图包含边u1u2,u11u14,vw,v11v12,w14w11的完美匹配数为c(n-1).

情形6 由a(n)的定义,G1图包含边u1u2,u11u13,vw,v11w14,w11w12的完美匹配数为a(n-1).

综上所述,

a(n)=4a(n-1)+2c(n-1).

(1)

G3图的完美匹配按饱和顶点u1可分以下8种情形求得：

情形1 由c(n)的定义,G3图包含边u1u11,u2u14,v11v12,w1w14,w2w11的完美匹配数为c(n-1).

情形2 由a(n)的定义,G3图包含边u1u11,u2u14,w1w2,v11w14,w11w12的完美匹配数为a(n-1).

情形3 由c(n)的定义,G3图包含边u1u11,u2u14,v11v12,w1w2,w14w11的完美匹配数为c(n-1).

情形4 由c(n)的定义,G3图包含边u1u2,u11u14,v11v12,w1w2,w14w11的完美匹配数为c(n-1).

情形5 由c(n)的定义,G3图包含边u1u2,u11u14,v11v12,w1w14,w2w11的完美匹配数为c(n-1).

情形6 由a(n)的定义,G3图包含边u1u2,u11u14,v11w14,w1w2,w11w12的完美匹配数为a(n-1).

情形7 由b(n)的定义,G3图包含边u1u2,u11u12,u14v11,w1w14,w2w11的完美匹配数为b(n-1),又a(n)=b(n),所以b(n-1)=a(n-1).

情形8 由b(n)的定义,G3图包含边u1u2,u11u12,u14v11,w1w2,w14w11的完美匹配数为b(n-1),又a(n)=b(n),所以b(n-1)=a(n-1).

综上所述,

c(n)=4a(n-1)+4c(n-1).

(2)

4-1-nC10图的完美匹配按饱和顶点u11可分以下5种情形求得:

情形1 由c(n)的定义,4-1-nC10图包含边u11w11,u14w14,v11v12的完美匹配数为c(n-1).

情形2 由a(n)的定义,4-1-nC10图包含边u11u14,v11w14,w11w12的完美匹配数为a(n-1).

情形3 由c(n)的定义,4-1-nC10图包含边u11u14,w11v12,w14w11的完美匹配数为c(n-1).

情形4 由b(n)的定义,4-1-nC10图包含边u11u12,u14v11,w14w11的完美匹配数为b(n-1),又a(n)=b(n),所以b(n-1)=a(n-1).

情形5 4-1-nC10图的完美匹配包含边u11u12,u14w14,v11v12,w11w12,则该完美匹配一定包含边ui3ui+1,4,wi3wi+1,4,ui+1,1ui+1,2,vi+1,1vi+1,2,wi+1,1wi+1,2,i=1,2,…,n-1.所以4-1-nC10图包含边u11u12,u14w14,v11v12,w11w12的完美匹配恰有1个.

综上所述,

f(n)=2a(n-1)+2c(n-1)+1.

(3)

将式(1)和(2)代入式(3),得

f(n)=16a(n-2)+12c(n-2)+1,

(4)

由式(3)得

f(n-1)=2a(n-2)+2c(n-2)+1,

(5)

式(4)-式(5)×8得

f(n)=8f(n-1)-4c(n-2)-7.

(6)

由式(2)和(3)得

c(n)=2f(n)-2,

(7)

由式(6)和(7)得

f(n)=8f(n-1)-8f(n-2)+1.

(8)

易知非齐次线性递推式(8)的特解为1.

齐次线性递推式f(n)=8f(n-1)-8f(n-2)的通解为

(9)

图6 图4-1-1×C10的所有完美对集Fig.6 All perfect matchings of 4-1-1×C10 graph

由图6知f(1)=7.由式(3)知，

f(2)=2a(1)+2c(1)+1.

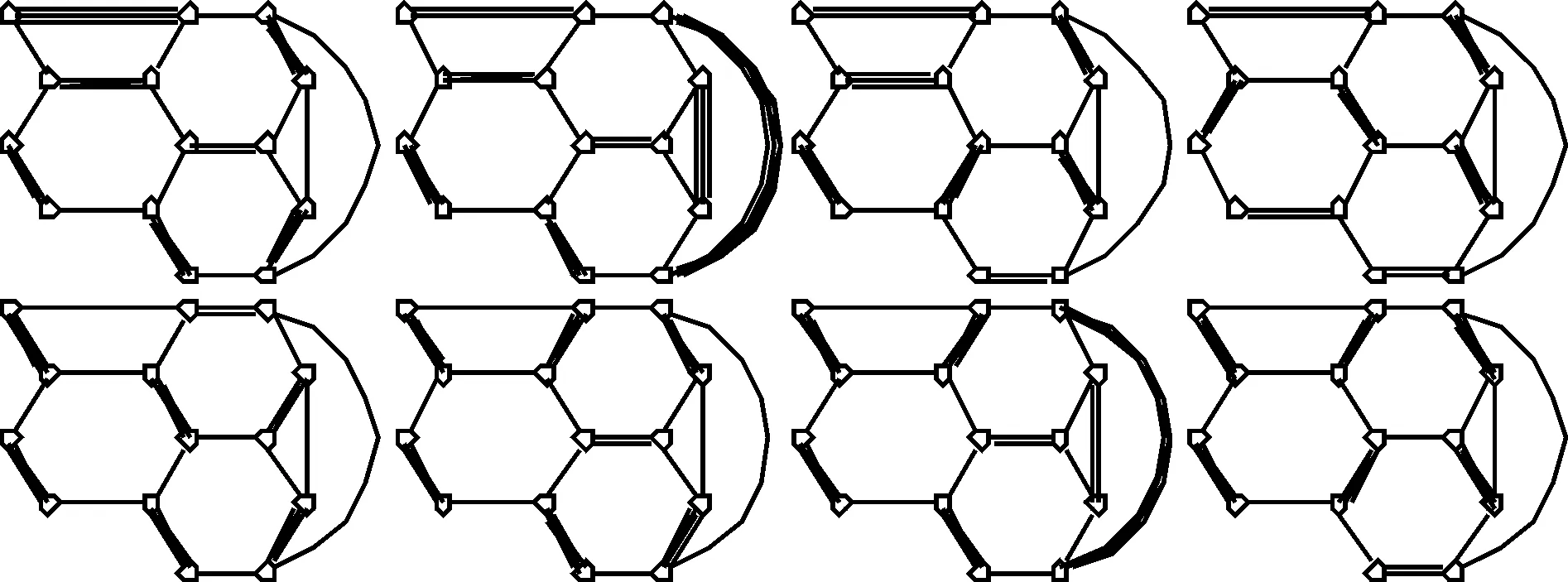
图7 G4图Fig.7 Graph of G4

由图7知a(1)=8.

图8 G5图Fig.8 Graph of G5

由图8知c(1)=12.所以，

f(2)=2×8+2×12+1=41.因此,线性递推式(8)满足f(1)=7,f(2)=41的解为

定理2g(n)表示2-nT2图的完美匹配数目,则g(n)=3n+1.

证明 2-nT2图是2边连通3正则图,显然存在完美匹配.为求g(n),先定义G6图.删除2-nT2图的边u11u13得到的图记为G6,如图9所示.

图9 G6图Fig.9 Graph of G6

显然，G6图存在完美匹配，其完美匹配数记为d(n).G6图的完美匹配按饱和顶点u11的情况可分以下3种情形求得:

情形1 由d(n)的定义,G6图包含边u11v11,u12v12,u13v13的完美匹配数为d(n-1).

情形2 由d(n)的定义,G6图包含边u11v11,u12u13,v12v13的完美匹配数为d(n-1).

情形3 由d(n)的定义,G6图包含边u11u12,v11v12,u13v13的完美匹配数为d(n-1).

综上所述,d(n)=3d(n-1)=3n-1·d(1)，易知

d(1)=3,所以d(n)=3n.

(10)

2-nT2图的完美匹配按饱和顶点u11可分以下4种情形求得:

情形1 2-nT2图的完美匹配包含边u11u13,则其必包含边ui2vi2(i=1,2,…,n),vi1ui+11,vi3ui+13(i=1,2,…,n-1),vn1vn3.所以2-nT2图包含边u11u13的完美匹配恰有一个.

情形2 由d(n)的定义,2-nT2图包含边u11u12,v11v12,u13v13的完美匹配数为d(n-1).

情形3 由d(n)的定义,2-nT2图包含边u11v11,u12v12,u13v13的完美匹配数为d(n-1).

情形4 由d(n)的定义,2-nT2图包含边u11v11,u12u13,v12v13的完美匹配数为d(n-1).

综上所述,

g(n)=3d(n-1)+1.

(11)

由式(10)和(11), 得g(n)=3n+1.

[1]LOVSZL,PLUMMERM. Matching Theory [M]. New York: North-Holland Press,1986.

[3] KARDOS F, KRL D, MISKUF J, et al. Fullerene graphs have exponentially many perfect matchings[J].Journal of Mathematical Chemistry,2009,46:443-447.

[4] 唐保祥,任韩.几类图完美匹配的数目[J].南京师大学报:自然科学版,2010,33(3):1-6. TANG B X, REN H. The number of perfect matching for three specific types of graphs [J].Journal of Nanjing Normal University: Natural Science Edition,2010,33(3):1-6.

[5] 唐保祥,李刚,任韩.3类图完美匹配的数目[J].浙江大学学报:理学版,2011,38(4):387-390. TANG B X, LI G, REN H. The number of perfect matching for three specific types of graphs[J].Journal of Zhejiang University: Science Edition,2011,38(4):387-390.

[6] 唐保祥,任韩.3类特殊图完美对集数的计算[J].南开大学学报:自然科学版,2014,47(5):11-16. TANG B X, REN H. The enumeration of perfect matchings in three types of special graphs[J]. Acta Scientiarum Naturalium Universitatis Nankaiensis,2014,47(5):11-16.

[7] 唐保祥,任韩.4类图完美匹配数目的递推求法[J].数学杂志,2015,353(2):626-634. TANG B X, REN H. Recursive method for finding the number of perfect matchings of the four types of graphs[J]. Journal of Mathematics,2015,353(2):626-634.

[8] 唐保祥,任韩.4类图完美匹配的计数[J].武汉大学学报:理学版,2012,58(5):441-446. TANG B X, REN H. The number of perfect matchings in four types of graphs[J]. Journal of Wuhan University: Natural Science Edition,2011,58(5):441-446.

[9] 唐保祥,任韩.5类图完美匹配的计数[J].中山大学学报:自然科学版,2012,51(4):31-37. TANG B X, REN H. The number of perfect matchings in five types of graphs[J]. Acta Scientiarum Naturalium Universitatis Sunyatseni,2012,51(4):31-37.

The number of perfect matchings in two types of particular graphs.

TANG Baoxiang1, REN Han2

(1.SchoolofMathematicsandStatistics,TianshuiNormalUniversity,Tianshui741001,GansuProvince,China; 2.DepartmentofMathematics,EastChinaNormalUniversity,Shanghai200062 ,China)

Perfect matching counting problems for graphs have been proven to be NP-hard, so it is very difficult to get the number of perfectly matched general graph. The counting formula of the perfect matching for graphs 4-1-nC10and 2-nT2was made by applying partition, summation and re-recursion. The number of all perfect matchings of many graphs can be calculated by the method presented in this paper. The given method is also able to implement the possibility to obtain the number of all perfect matchings with perfect matching graphs.

partition; recurrence relation; perfect matching