流体致旋转磁场微型发电系统仿真设计

陈嘉伟,杨 慕，倪其军

(1.中国船舶科学研究中心，无锡 214082；2.中国长城工业集团有限公司，北京 100054)

流体致旋转磁场微型发电系统仿真设计

陈嘉伟1,杨 慕2，倪其军1

(1.中国船舶科学研究中心，无锡 214082；2.中国长城工业集团有限公司，北京 100054)

以海洋流致旋转磁场微型发电系统为对象，利用CFD软件对海流能发电机的关键部件的力学性能、发电机的电磁性能实现了仿真设计和动态模拟。在模拟水轮在水流冲击下的运动时使用了旋转坐标系法，得到了水轮转速与输出功率的关系，为发电机的设计提供了依据。利用磁宏得到所建路径上的齿磁通，从而求出了发电机的空载电压，为进一步优化设计发电机、提高发电效率提供了直观的依据。

CFD；动坐标法；齿磁通；磁宏

现代清洁能源的研究如火如荼，海流能是一种清洁能源，且洋流能与其他清洁能源相比能量密度更大，英国目前在洋流发电技术上处于世界领先地位，2003年MCT联合多家公司研制的“世界首台称为商业规模的水平轴式潮流发电装置”，安装在英国布里斯托尔海峡进行试验，装机容量300KW，其改进型装置目前正在研制中[1]。

2007年，美国Verdant Power公司在纽约东海岸建成6台35kW的机组，并计划将在2020年前完成200至300台机组的水下发电场的建设。由此可见，水下风车将逐步成为大规模利用海流发电的有效途径之一[2]。

在国内，东北师范大学在2005年主持并完成了由国家“863 计划”课题“海洋水下仪器能源补充技术”，主要是通过海流能发电装置给水下仪器提供能源[3]。浙江大学在2007年研制出额定功率为5KW 的的水下风车海流能发电机模型样机[4]。

本文设计一种可利用洋流能发电的微型发电机，并对此流体旋转磁场的微型发电系统进行设计和仿真研究，为洋流能的开发利用提供一种可行方案。该洋流发电机体积小，维护简单，可以用于为海上浮标供电，也可以安装在海上平台的周围海域，为海上平台供应电能，为海上设备提供绿色电能。

1 整体方案的设计

1.1 导流罩的设计和仿真

洋流的流速平均约为0.5m/s，为了提高海流的能量密度，需要添加导流罩将海水加速，设计的导流罩2D如图1所示。在 2D 情况下，入口为 0.5m/s 时，可以将来流提高到 1.0m/s 左右，推出在 3D 中模型中，使用该导流罩可以将流速提高到约 2m/s。

图1 2D导流罩模型水流速度分布图

1.2 发电机的模型设计

在海水中线圈绕组需要很好的密封，为此采用旋转磁场法，将永磁磁极固定在转子周围，线圈绕组(定子)密封好套在导流罩上如下图2所示。

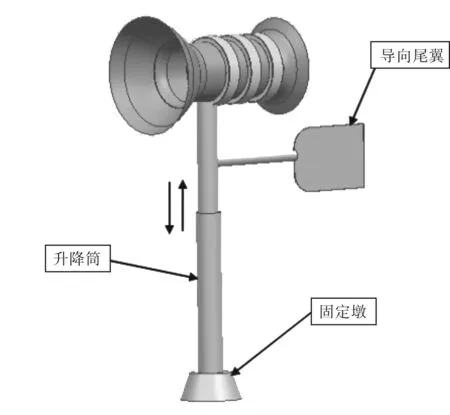
图3 整体发电机组模型示意图

为了提高水能利用效率，可以将多个发电机组放在同一导流罩中，并配以固定墩、升降筒和导向尾翼，如图3所示。该方案主要的特点是叶轮带动磁极旋转，线圈绕组密封在导流罩周围，没有电刷，避免了有刷发电机可靠性差、易产生火花、维修频繁的缺点，适合在海下复杂的环境下工作。导向尾翼使导流罩总是迎着海流流入方向，升降筒使发电机能够露出海面，便于维修或收集发电机生产的氢、氨、甲醇等。

1.3 桨叶的设计

因为海流流速较慢，一般流速在0.9km/h-2.5km/h，为了简化问题，在设计翼型时，假设海流速度为0.5m/s。因为流速较低，故选择翼型厚度较小的NACA6306翼型[5]。在设计翼型轮廓时使用了Profili软件进行辅助设计，软件可以生成NACA6306翼型在不同雷诺数下攻角与升阻比的关系。

当流体速度为0.5m/s时，雷诺数Re大致在600000左右，可以得出该翼型获得最大升阻比( Cl/Cd 最大)时，攻角α=8.0°。当桨叶旋转时，相对速度决定了，桨叶的安装角要大于这个值，在此取经验值15°。为了提高水轮的海流能利用效率，应该提高水轮的实度(即桨叶的轴向投影占投影面的比例),故采用6个桨叶。

2 对桨叶的动态仿真

2.1 仿真设计及模型建立

本设计的翼型结构利用Gambit中的Turbo工具栏进行建模和划分网格，在Fluent分析中为了模拟水流和叶片的相互作用，采用动坐标法。所谓动坐标法，就是赋予流场一定的转动速度，此时定义叶片、轮毂的速度为零(在绝对坐标系中的转速和流场转速相同)，然后得出在一定速度来流环境下的扭矩，根据式1可以得到水轮的机械功率，然后根据获得最大机械功率处的参数来作为设计发电机的依据[6-7]。

P=M*ω

(1)

其中：M为水轮扭矩，ω为水轮的角速度。

在本文的数值模拟中，流动采用非定常RANS(雷诺时均Navier-Stokes方程)方程模拟；选择SSTk-ω湍流模型，封闭RANS方程。

控制方程包括：连续性方程、RANS 方程、湍流模型SST 方程、Level-set方程。

(1) 连续性方程

(2)

(2)RANS方程

(3)

(3) SSTk-ω湍流模型

SSTk-ω模型是在标准k-ω模型的基础上做了改进。本质上，SSTk-ω模型是标准k-ω和k-ε的混合模型，从边界层内部的标准k-ω到边界层外部的高雷诺数的k-ε逐渐转变；SSTk-ω合并了来源于ω方程中的交叉扩散，且它的湍流黏度考虑到了湍流剪应力的传播，修改了湍流黏性公式。这些改进使得SSTk-ω比标准k-ω在广泛的流动领域中有更高的精度和可信度。湍流动能k方程：

(4)

特殊耗散率ω方程：

(5)

式中Tk,Γω为k和ω的扩散系数，Gk,Gω为湍流产生项，Yk,Yω为湍流耗散项。

因为海流速度较慢，所以采用导流罩来增大流过水轮的海流速度，经模拟可以获得流速为 2m/s 的流速。采用旋转坐标法，在 2m/s 的来流条件下，依次求解转速为 0rad/s、0.5rad/s、1rad/s、2rad/s、2.5rad/s、3ad/s、4rad/s、5rad/s、6rad/s、8rad/s、10rad/s、12rad/s、14rad/s的情况下水轮的转矩大小。

2.2 仿真结果分析

表1是模拟所得的水轮在不同转速时输出的转矩和功率数据。由表中数据得出该水轮在 2m/s 的水流中最大转速在 5rad/s 左右，而当水轮转速超过6rad/s时，水轮对水有推动作用，这与事实不符，所以超过6rad/s时的数据为无效数据。在Matlab中对数据进行拟合、插值得到图4，通过图4可知在转速为2.7rad/s 时，该水轮有最大能量转化效率，此时功率约为39.36W，并通过Fluent 中Turbo分析工具可以得到此时的效率约为48%。

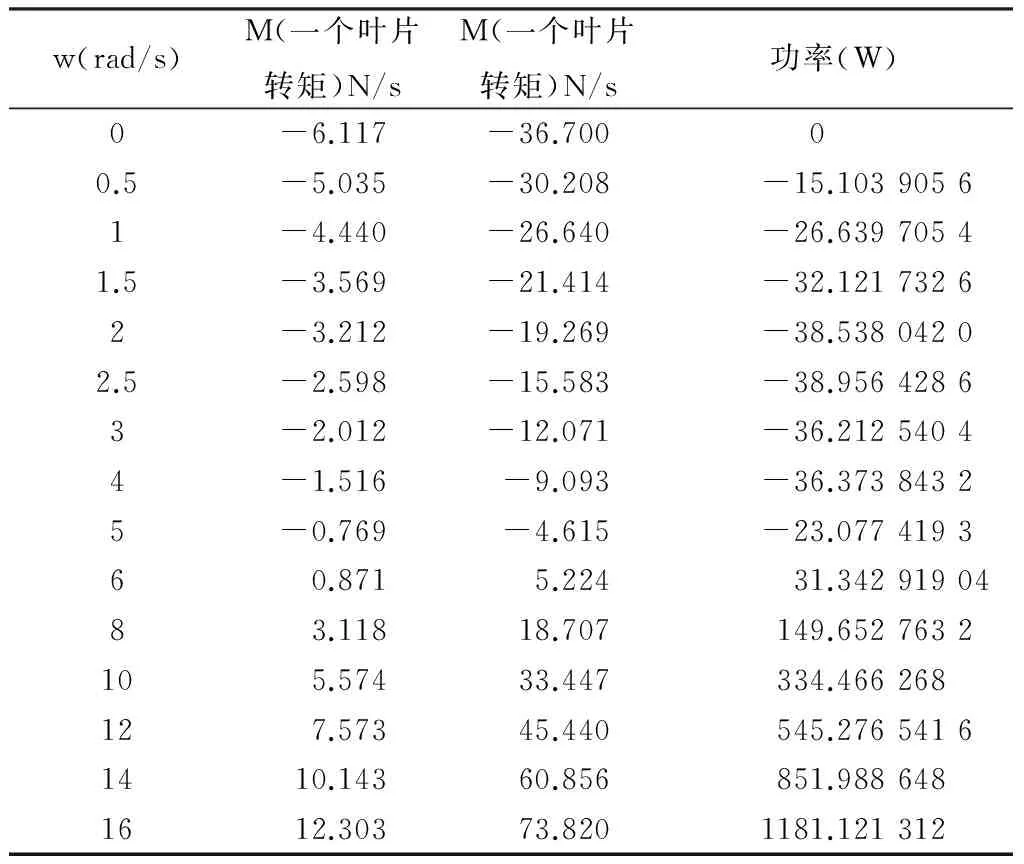
表1 在2m/s来流中水轮转速与输出的转矩、功率

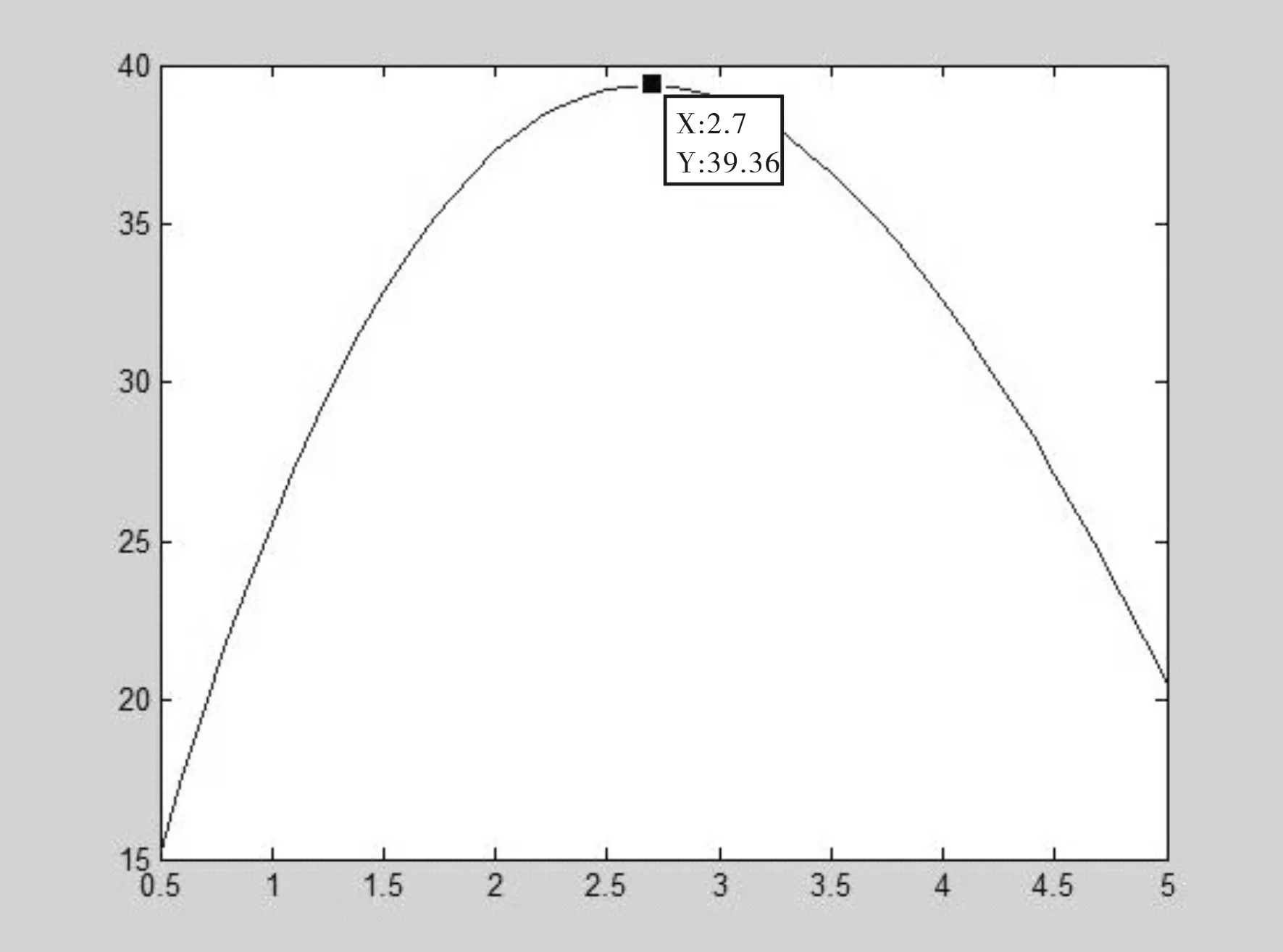
图4 水轮转速与输出功率的关系图

3 发电机的设计和仿真

3.1 发电机仿真方案设计

本文采用二维场模拟实际磁场，采用MSK国际单位制和笛卡尔直角坐标系，并假设不计交变电流在导电材料中的涡流反应，忽略转配误差，假定材料的磁导率是各项同性的。发电机二维模型图如图2所示：该发电机模型共4对磁极，24个线圈槽，所以定子上每个齿的夹角为15度。线圈槽形状采用简单的矩形直槽，纵向长度为100mm，定子最大直径为110mm，转子上有永磁磁极[8]。

该发电机模型可以只分析其1/4周期内各个齿的磁通量，为了求得齿磁通随转子的位置变化关系，将一个定子齿距分为10等份，每一段对应的机械转角为1.5°。转子每转过1.5°，计算此时的磁场，得到1/4周期内六个齿各自的磁通量。转子转过一个定子齿距，即10个位置之后，得到6个齿在11个不同位置的齿磁通，可以表示为向量的形式：Φj=[Φj0,Φj1,Φj2…Φj10]，其中j为齿的序号(j=1,2,3…6)。当转子转过一个齿距后，下一个齿会重复上一个齿的行程，使磁通量呈周期性变化[9]。

根据法拉第电磁感应定律，绕组的感应电动势可由下式得到：

e=-dΦ/dt=-dΦ/dθ·θ/dt

=-ω·(dΦ/dθ)

(6)

式中ω为发电机转子的转动角速度，单位为rad/s，Φ为磁通量，单位为Wb/m。

得到转子处于不同位置的齿磁通量后，绕组电动势的第j个元素，即第j个位置的感应电动势可由下式计算：

ej=-w·(Φj+1-Φj)/(θj+1-θj)

(7)

假设发电机正常工作时的加速度w=2.5rad/s，发电机的轴向长度取 0.1m，对于该模型式子可以记作：

ej=-2.5*1.5*0.1*(Φj+1-Φj)

=-0.375*(Φj+1-Φj)

(8)

3.2 仿真结果分析

图5是在1/4圈即1个周期内，齿1到齿6在θ=0°位置的气隙磁通量大小变化曲线。从这组气隙变化图可以看出，齿1和齿4、齿 2 和齿5、齿3和齿6的磁通量分布对称，变化趋势恰好相反，所以它们的感应电动势大小相同、符号相反，可以用绕组将其连接在一起，使整个发电机构成三相交流电输出。

图6a是六个齿单匝绕组的空载电压随时间变化曲线，从图中可以看出电压波动比较大。但是在实际中发电机绕组线圈有电感，以及后续的滤波整流电路的作用可以使电压呈光顺规律的变化。本文通过Matlab的拟合命令，对曲线进行多项式拟合处理，结果如图6b所示，为多项式拟合的 1/4 周期内六个齿绕组电压变化曲线。该曲线为时间和电压以五次多项式拟合和插值的曲线，从中可以看出，在一个完整周期内，曲线近似呈三角函数变化，且齿1和齿4、齿2和齿5、齿3和齿6的图线恰好相反，因此可以用三角函数表示出齿1、齿 2、齿3的变化规律，就可以知道发电机所有齿绕组的电压变化规律了，在此采用利用特殊点来推出三角函数。下面以绕组2为例，说明找出电压变化的三角函数关系式过程。

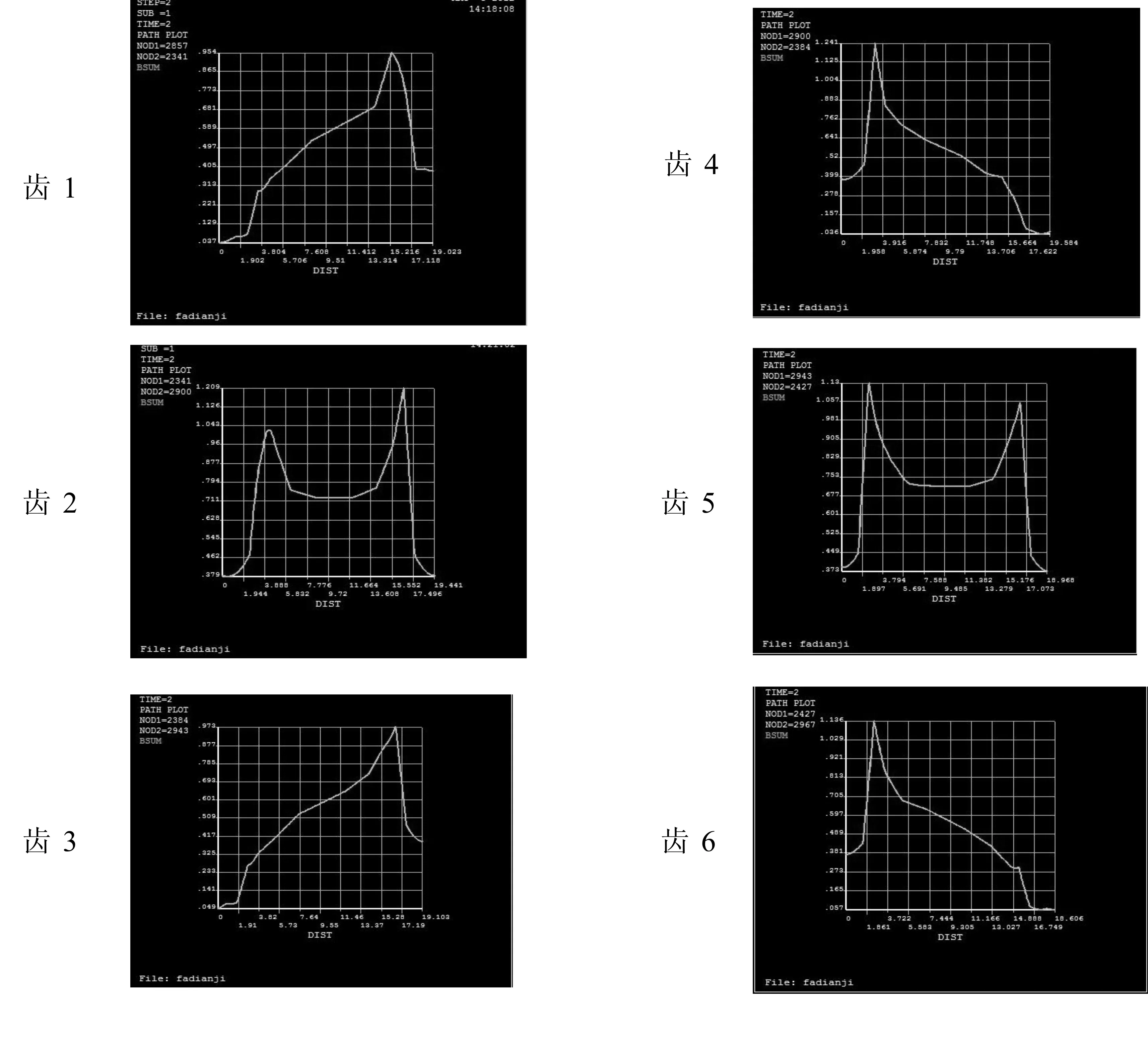
图5 θ=0°时齿1至齿6间的气隙磁通量大小变化图

如图7所示，在齿绕组2的多项式拟合电压变化曲线上选取的四个特殊点，由图所示的四个捕捉点可知T=0.658s-0.017s=0.631s，w=2π/T≈ 9.96rad/s，振幅A=(1.52+1.55)/2=1.535,可以得到此绕组电压的三角函数近似为：

U2=1.535sin(9.96t-0.17)

绕组2电压变化的多项式拟合曲线与三角函数拟合曲线可以看出两者误差不大，近似性较好。那么齿4的空载电动势可记作：

U3=-1.535sin(9.96t-0.17)

由发电机原理和结构可以得知U1、U3的周期同U2相同，同理，按照相同方法可以分别得到齿2、齿3的空载电动势函数。

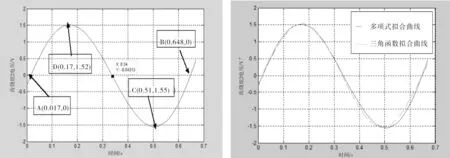
图7 绕组2电压变化的多项式拟合曲线与三角函数拟合曲线

在整个发电机中将其他周期里与绕组1，绕组 4 的变化规律相同的绕组串联构成一相电，其他两对亦是如此连接，这样发电机输出的三相空载电压函数为：

4 结论

(1)桨叶是海流能发电机最关键的部件之一，本设计根据海流流速设计了一个扭转角为 75 度、叶片数为6的水轮，在 Fluent 中模拟了该水轮在 2m/s 的来流下，输出扭矩与转速的关系。

(2)利用Ansys模拟了发电机在2.5rad/s的转速下空载电压特性，得到了此设计的三相空载电压函数。发现发电机的气隙对磁路影响很大，气隙越小漏磁越少，但是在实际环境下应考虑，防止杂物阻塞气隙，此外本设计中的发电机的极槽配合还不太理想，导致电磁转矩波动较大，这不利于发电机正常工作，因此发电机结构有待优化。

[1]张健.国际电力资讯[J].陕西电力，2008(3)：85-85.

[2]余国锋.水轮发电机组大波动过渡过程计算模拟仿真研究[J].能源研究与信息,2014,30(1):35-38.

[3]张萧.海流能发电及模拟装置的研制[J].东北师范大学学报：工学报,2009，54(4):4-6.

[4]林永刚,李伟.水下风车海流能发电技术[J].浙江大学学报：工学版,2008(7)：1242-1246.

[5]赵盛萍. 650MW水轮机调节系统非线性模型研究[J]. 能源研究与信息，2014,30(1):39-42.

[6]梁京辉,张晓锋.离散式任意充磁角度Halbach永磁电机解析模型研究[J].物理学报,2013,62(15):87-89.

[7]李健,李佳.一种洋流发电涡轮机转子设计方法及试验验证[J].水电能源科学,2014(4):180-183.

[8]王丽华.基于ANSYS二次开发的永磁同步发电机电磁场分析[J].电气技术,2014(8):40-42.

[9]刘国清.基于Ansys永磁同步发电机的电磁分析[J].机械工程技术，2010，39(5):68-70.

(责任编辑 赵冰)

A Simulation Design of the Minisize Power Generation System whose Magnetic Field is rotated by Fluid

CHEN Jia-wei1, YANG Mu2,Ni Qi-jun1

(1.China Ship Scientific Research Center, Wuxi 214082, China； 2.China Great Wall Industry Corporation, Beijing 10054, China)

This paper chooses the minisize power generation system as object, doing the simulation design and dynamic simulation on the key mechanical component’s properties and the electromagnetic properties of ocean current energy generator with computational fluid dynamics (CFD). Using the rotating coordinate system in a simulated water wheel in the water under the impact of the movement, it is easy to find that the relationship between water wheel rotational speed and output power that providing a basis for the design of the generator. Use the magnetic macro built on the path of magnetic; the paper gets the generator’s no-load voltage. The result provides an intuitive basis on optimizing the design generator and enhancing its power generation efficiency.

moving coordinate method; CFD; tooth flux; magnetic macro

2017-02-03

陈嘉伟(1990—)，男，江苏无锡人，硕士，中国船舶科学研究中心工程师，主要从事船舶与海洋工程设计、计算流体力学能等方面的研究。

10.13783/j.cnki.cn41-1275/g4.2017.02.028

TM612

A

1008-3715(2017)02-0124-05