活用等效思想,巧解直流电路问题
2017-05-17重庆市万州高级中学高2018级19班404020周国强
重庆市万州高级中学高2018级19班(404020) 周国强●
活用等效思想,巧解直流电路问题
重庆市万州高级中学高2018级19班(404020)
周国强●
直流电路问题是高考必考的内容,也是高中部分对电路的重点讨论部分,其中的闭合电路欧姆定律以及其他内容是非常重要的.而等效思想与这些知识的结合开创了一个新的解题思路,也出现了一系列技巧性很强的问题.本文主要结合等效思想分三种不同的电路中常见的问题进行举例说明,希望学生好好体会,定有收获.
一、等效法求电路外电阻问题
电阻的等效是最为常见的也是最基本的等效问题,等效电阻对于我们简化复杂的电路图以及求解其他电路问题时有重要的作用,是解题的基础.我们只要保证等效前后电阻的总值不变即可,这是等效的前提条件.
例1 如图1所示,电阻R1~R6的电阻分别为4Ω、6Ω、12Ω、8Ω、10Ω、7.2Ω,求RAB得阻值.
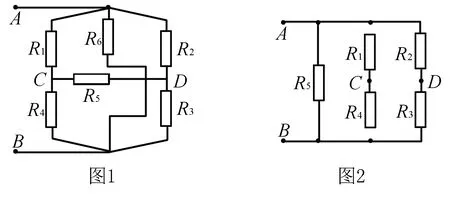
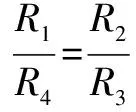
点拨 这种等效是我们在解题中非常容易遇到的情况,在判断电阻实际上是否接入电路中时我们要判断其两端的电压是否存在,不存在电压是不存在电流的,也就是说电阻是并未起作用的,这时就可以直接省略了.
二、等效法求电源功率问题
在高中物理中除非特殊指出,否则一般的电源都是有内阻的.而电源功率是指电源向外电路输出的功率,并非是电源内阻所损耗的功率,这是最容易混淆的一点,也是题中经常出现的考点,学生要了解电源功率与外电路电阻之间的关系才能正确解题.
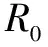
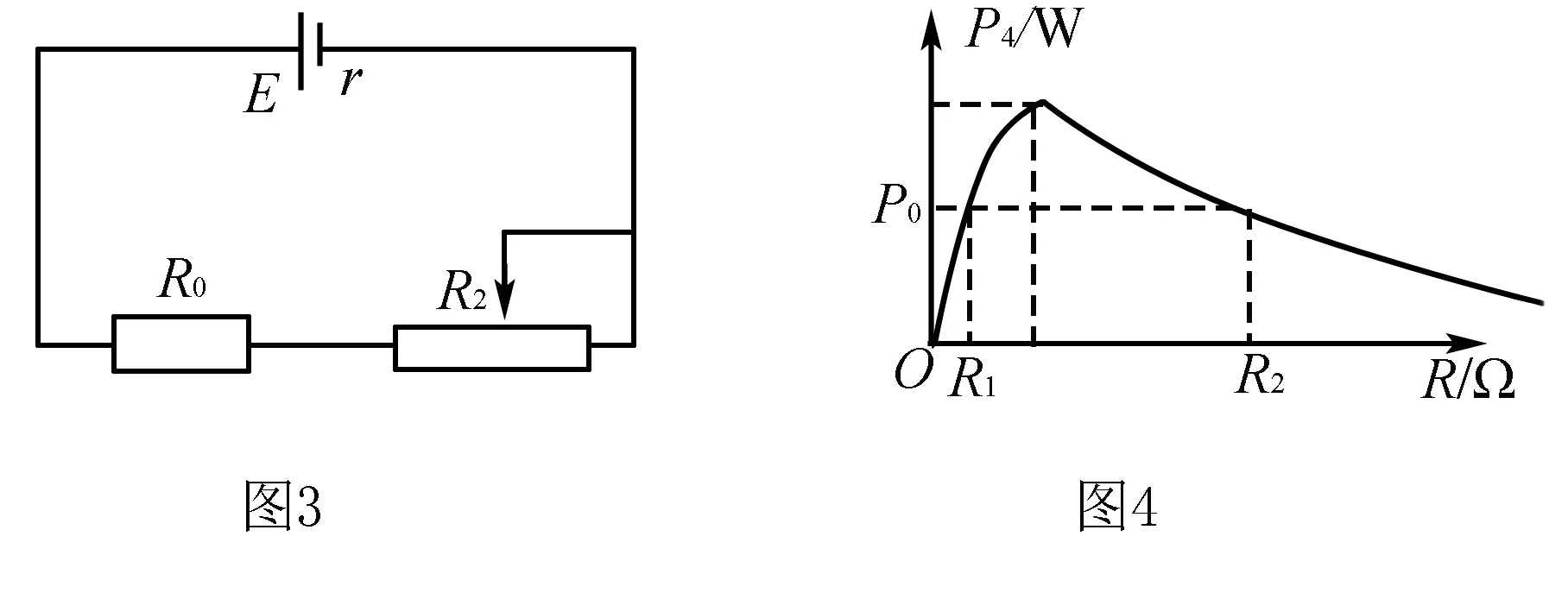
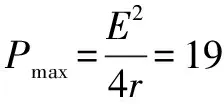
点拨 本题中的电源内阻大于定值电阻R0采用此种解法,但是当内阻小于内阻时就不能实现外电阻等于内电阻了,因为当滑动变阻器为0时外电阻还是比内阻大,这时就需要对曲线有深刻的理解了,学生可以自行讨论此种情况.
三、等效法解电阻功率问题
这里的电阻就是除内阻外的电阻了,但是与电源功率不同的是此种情况下的电阻功率是外电路中某一个电阻的功率问题,这是题目的设定在外电路中总是存在多个电阻,我们要合理等效才能使题目得到正确的简化求解.
例3 如图5所示,电动势为10V,内阻r=1Ω,R1=1Ω,R2=2Ω,R3=3Ω.当R4为何值时其本身消耗的功率为最大值,并且求其最大功率以及这时本身两端的电压为多大.
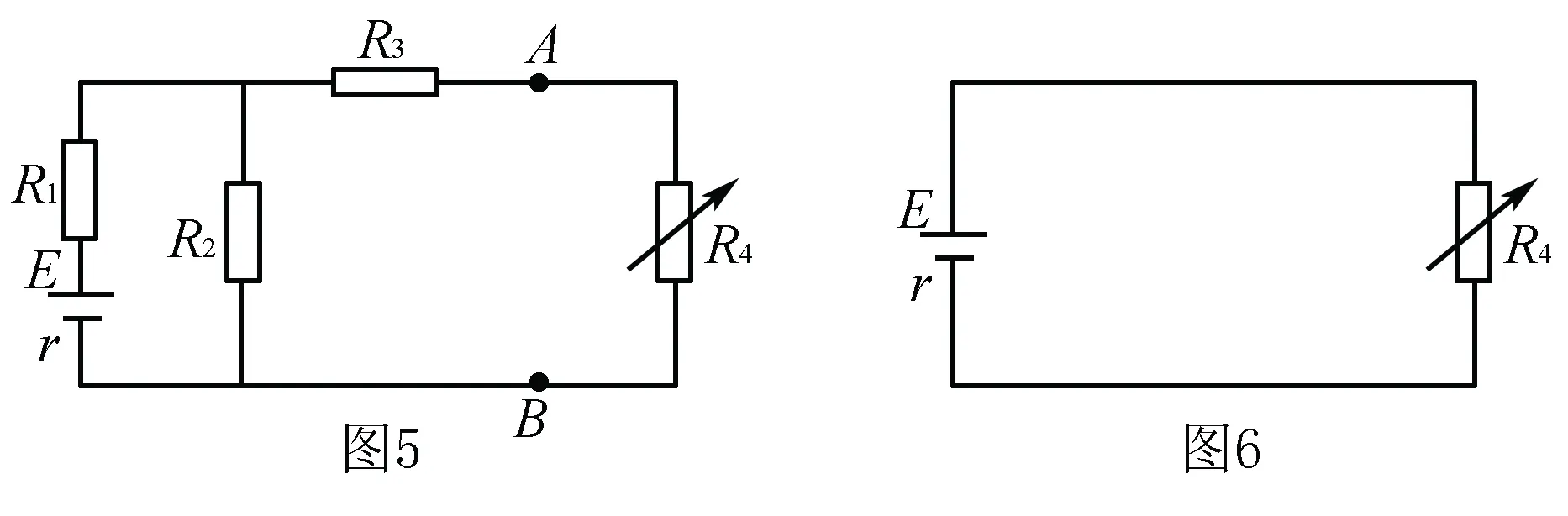
解析 本题就是典型的等效法求解问题,因为如果不运用适当的等效直接借助闭合电路欧姆定律求解会非常繁琐,涉及很多个电阻,这显然不是出题者想考察的.采用等效电源模型的方法可以很好的解决此类问题.我们在学习中知道当外电阻等于电源内阻时电源输出功率有最大值.虽然此题中并不是求电源功率,但是我们可以将除了R4之外的电阻和电源之间进行等效,形成如图6所示的等效电源.这时等效电源两端的电压就是R4本身的电压,我们只要使R4=r′就可以了.接下来我们求等效的电源内阻的值r′=4Ω,这是不难求出的.接下来的功率以及电压就不难求出了,学生自行求解写出答案即可.
点拨 本题的巧妙之处就是等效电路的思想,这在恒定电流的考察中是非常重要的,也是我们必须掌握的技巧,只有合理的对问题进行等效,才能准确快速的得出结论,学生要对此反复练习,实现举一反三.
总之,等效法在对电路中的电阻、电压、功率等问题的求解都有很大的帮助,可以说等效思想能否灵活运用是我们能否快速准确解题的关键,学生要开动自己的思维,并且探索经验,形成自己的解题思路.
G
B
1008-0333(2017)10-0069-01
